Похожие презентации:
Применение производной
1.
Применениепроизводной
2.
Производная может применяться для:1) нахождения уравнения касательной и
нормали к графику функции;
2) исследования на монотонность;
3) нахождения экстремумов функции;
4) нахождения наибольшего и наименьшего
значения функции на отрезке.
3.
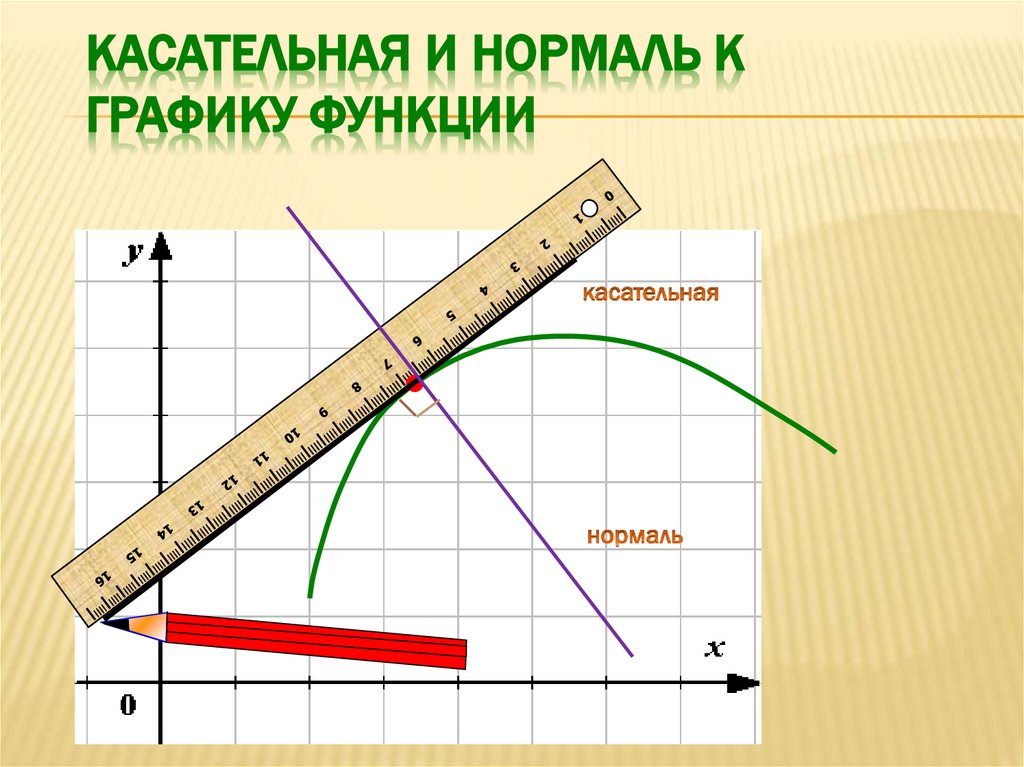
КАСАТЕЛЬНАЯ И НОРМАЛЬ КГРАФИКУ ФУНКЦИИ
4.
yк f ( x0 ) f ( x0 )( x x0 )1
у н f ( x0 )
( x x0 )
f ( x0 )
5.
ЗАПИШЕМ, ЧТО ОЗНАЧАЕТ КАЖДАЯ ЗАПИСЬ ВФОРМУЛАХ
1) f(x ) - значение функции в заданной точке;
2)
- значение производной в заданной
точке;
3) Х – неизменяемая переменная;
4) x – заданное значение переменной.
0
0
6.
1) УРАВНЕНИЕ КАСАТЕЛЬНОЙ (НОРМАЛИ) КГРАФИКУ ФУНКЦИИ
Алгоритм нахождения:
1) Найти значение функции в заданной точке;
2) Найти производную функции;
3) Найти значение производной в заданной точке;
4) Написать уравнение касательной к графику
функции;
5) Написать уравнение нормали к графику
функции.
7.
2) ИССЛЕДОВАНИЕ НА МОНОТОННОСТЬ:Признак возрастания функции: если
производная на некотором промежутке
положительная, то функция возрастает на
этом промежутке.
Признак убывания функции: если
производная на некотором промежутке
отрицательная, то функция убывает на этом
промежутке.
8.
МОНОТОННОСТЬ ФУНКЦИИАлгоритм нахождения промежутков убывания и возрастания
1) Найти производную функции;
2) Найти стационарные и критические точки, приравняв
производную к нулю;
3) Разместить полученные точки на числовой оси, определить
знак производной и поведение функции на образовавшихся
промежутках;
4) Определить характер промежутков (возрастает, убывает)
5) Записать результат
9.
3) ЭКСТРЕМУМЫ ФУНКЦИИ(ТОЧКИ МАКСИМУМА И МИНИМУМА)
Если при переходе через стационарную точку
функция и производная меняют знак с
«плюса» на «минус», то стационарная точка
является точкой максимума.
Если при переходе через стационарную точку
функция и производная меняют знак с
«минуса» на «плюс», то стационарная точка
является точкой минимума.
10.
НАХОЖДЕНИЕ ТОЧЕК ЭКСТРЕМУМА ФУНКЦИИАлгоритм нахождения точек экстремума
1) Найти производную функции;
2) Найти стационарные и критические точки, приравняв
производную к нулю;
3) Разместить полученные точки на числовой оси и определить
знак производной на образовавшихся промежутках;
4) Определить характер точек (максимум и минимум)
5) Записать результат
11.
4) НАХОЖДЕНИЕ НАИБОЛЬШЕГО ИНАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ НА
ОТРЕЗКЕ
Алгоритм нахождения наибольшего и наименьшего значения
функции y=f(x) на отрезке [a, b]
1) Найти производную функции;
2) Найти стационарные и критические точки, приравняв
производную к нулю;
3) Определить принадлежность полученных точек отрезку [a, b];
4) Вычислить значение функции y=f(x) в отобранных точках и
на концах отрезка (в точках a и b);
5) выбрать среди них наибольшее и наименьшее значение
функции и записать результат










 Математика
Математика








