Домашнее задание №2 "Выбор методики расчёта коэффициента сверхсжимаемости газа"

1.

Технология эксплуатации газовых скважин
Домашнее задание №2
“Выбор методики расчёта
коэффициента сверхсжимаемости газа”

2.

Цель работы
Расчёт коэффициента сверхсжимаемости Z
смеси природного газа, используя различные
методики:
- по
графикам
Брауна-Катца
и
аппроксимационной зависимости этих графиков,
полученной Г. Гуревичем и В. Латоновым;
- по двух и трех параметрическим уравнениям
состояния
- по уравнениям Редлиха-Квонга и ПенгаРобинсона.

3.

Коэффициент сверхсжимаемости газа
– отношение объема V при заданных Р и
Т к объему этого газа, определенному при
идентичных Р и Т по законам идеального
газа Vид.
Z характеризует отклонение объема
реального газа от объема “идеального” газа.
Z = V/Vид

4.

Зависимость между давлением, объемом и
температурой называется уравнением состояния.
Двухпараметрические уравнения состояния
Наиболее распространенными в технологии
газовой промышленности является уравнение
Менделеева – Клайперона, которое с учетом
реальных свойств газа имеет вид:
PV=GRT
где Р – абс.давление, Па; V – объем, м3; R – удельная
газовая постоянная, кДж/(кг*К), Т – температура, К;
G – масса вещества, кг
R=8314 кДж/(кмоль*К)

5.

Z=PV/GRT=1
Z – коэффициент, характеризующий степень отклонения реального газа
от закона идеальных газов (к-т сверхсжимаемости).
Все реальные газы не подчиняются законам идеальных газов.
Голландский физик Ван-дер-Ваальс предложил учитывать объем собственных
молекул газа и силы их взаимного притяжения введением дополнительных членов в
уравнение Менделеева-Клайперона:
а
р
v b RT
2
v
где v – удельный объем газа, а/v2 – константа сцепления молекул, b – поправка на
объем молекул.
а/v2 выражает внутреннее давление, которое является равнодействующей сил
притяжения всех молекул в объеме v.
поправка на объем молекул b, имеющих шароообразную форму, равна
собственному объему молекул, увеличенному в 4 раза.
Уравнение Ван-дер-Ваальса приближенное, т.к. коэффициенты а и b – сложные
функции V, T , формы молекул газа.

6.

Коэффициент сверхсжимаемости газа
z
• СОСТАВА ГАЗА
ДАВЛЕНИЯ
ЗАВИСИТ
ОТ
• ТЕМПЕРАТУРЫ

7.

Графики Брауна и Катца
В большинстве случаев для определения
коэффициента сверхсжимаемости, содержащих
- не более 2% (мольных) высококипящих
углеводородов С5+,
- 2% ароматических углеводородов
- и около 5% полярных и кислых
компонентов, пользуются универсальными
графиками Брауна и Катца Z=f(Тпр, Рпр)

8.

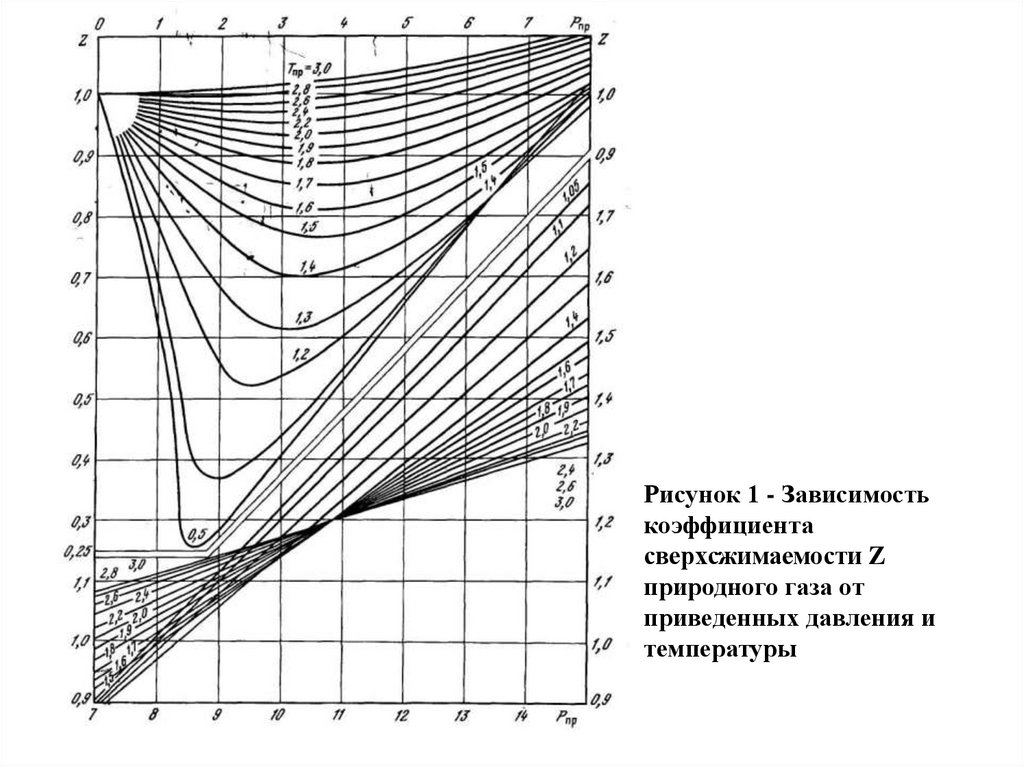
Рисунок 1 - Зависимость
коэффициента
сверхсжимаемости Z
природного газа от
приведенных давления и
температуры

9.

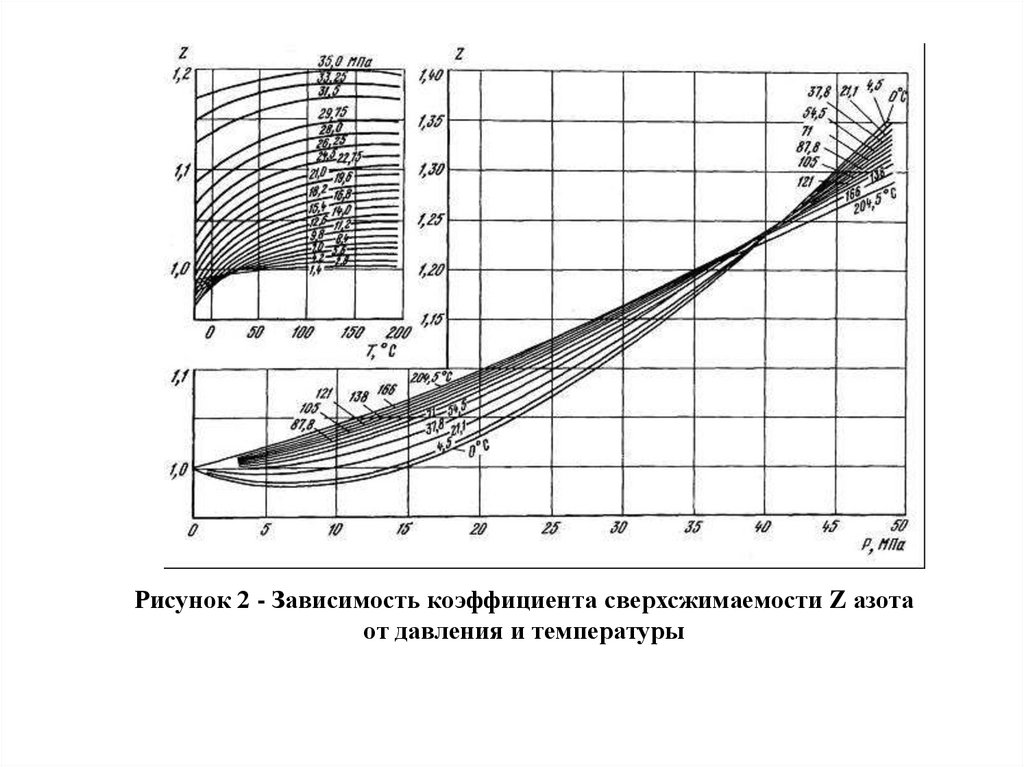
Рисунок 2 - Зависимость коэффициента сверхсжимаемости Z азота
от давления и температуры

10.

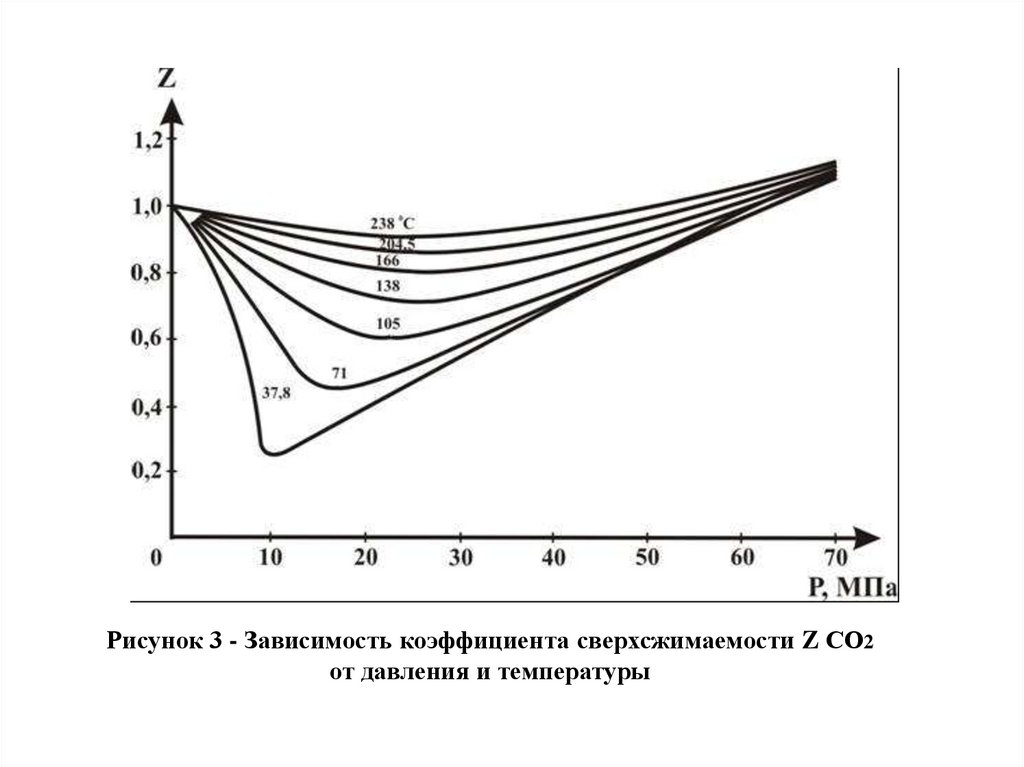
Рисунок 3 - Зависимость коэффициента сверхсжимаемости Z СО2
от давления и температуры

11.

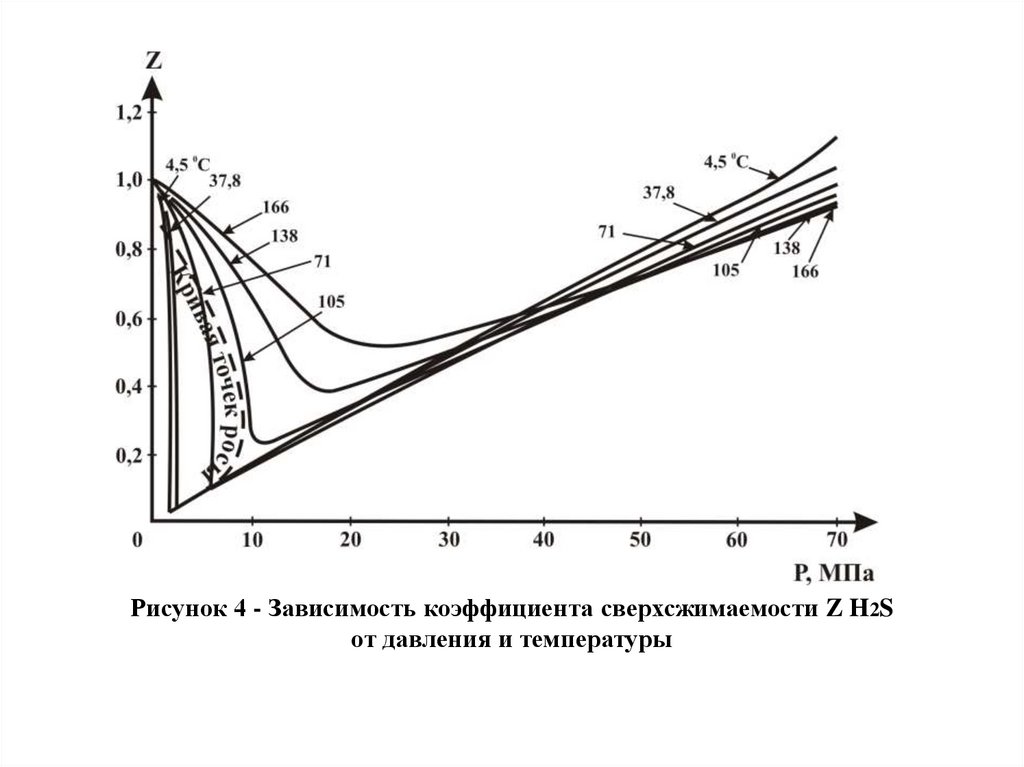
Рисунок 4 - Зависимость коэффициента сверхсжимаемости Z H2S
от давления и температуры

12.

Для оценочных расчетов пользуются аппроксимацией
графиков Брауна и Катца, предложенных Г. Гуревичем и В.
Латоновым в виде:
Z 0,4lg Т пр 0,73
Р пр
0,1Р пр

13.

Если в составе газа неуглеводородных и
тяжелых компонентов менее 10%, то для
определения Z с учетом двух параметров (Рпр и
Тпр)
используют
следующее
уравнение:
Z Zув x ув ZN2 x N2 ZCO2 x CO2 ZH2S x H2S
xN2, xCO2, xH2S– соответственно мольная доля азота,
углекислого газа и сероводорода в составе
природного газа. По зависимостям Z=Z(Рпр; Тпр),
показанным на рисунках выше определяют величину
Z для каждого неуглеводородного компонента

14.

Трехпараметрические уравнения
состояния
При более высоком содержании в газе высококипящих
углеводородов С5+ и полярных компонентов коэффициент
сверхсжимаемости Z следует определять с учетом фактора
ацентричности по формуле:
Z=Z(0)+ωсмZ(1)
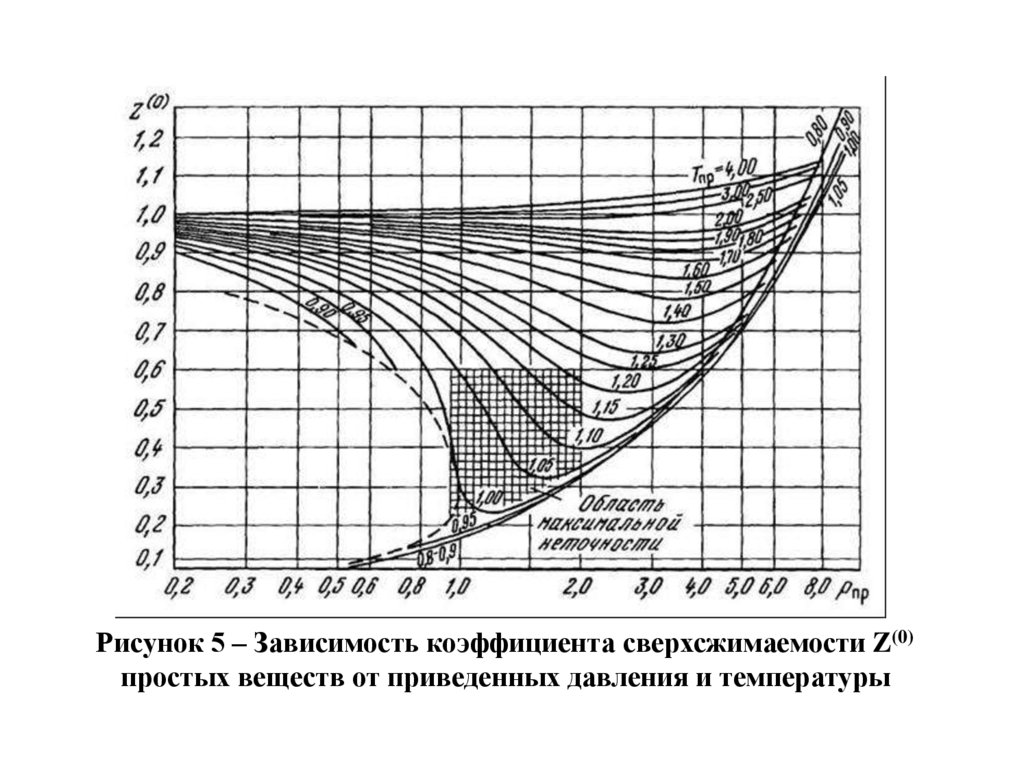
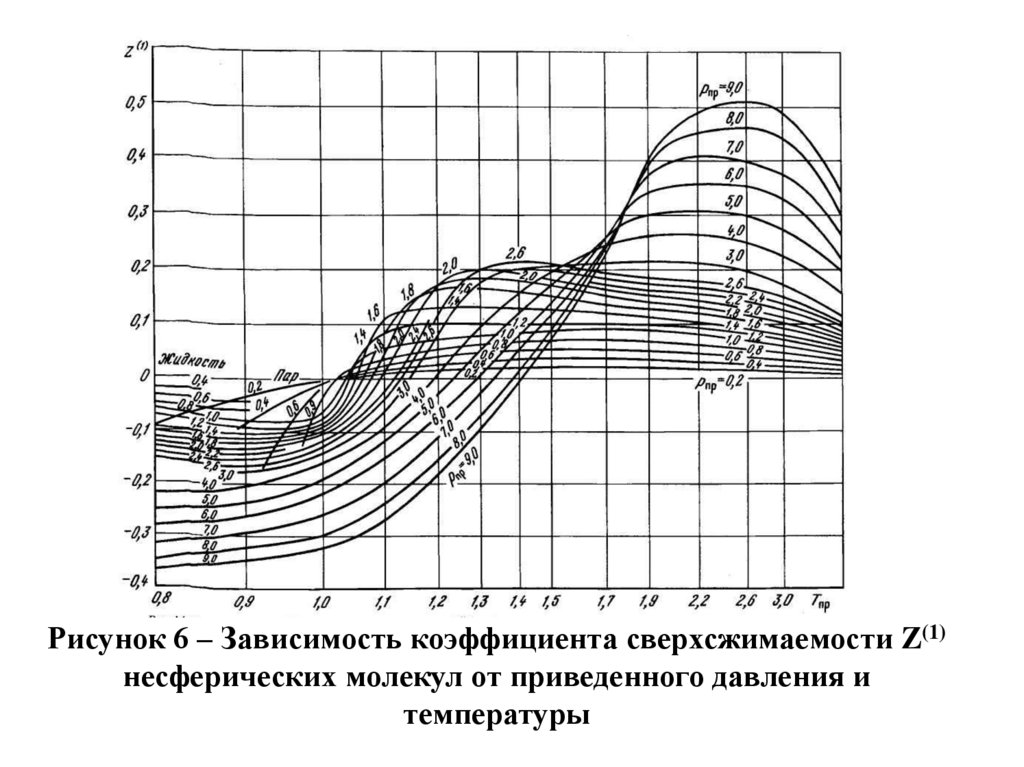
где Z(0), Z(1) – коэффициенты, определяемые из графиков
зависимостей Z(0) и Z(1) от приведенных параметров Рпр
и Тпр, показанных на рисунках 5 и 6; ωсм – фактор
ацентричности, определяемый по известному составу
n
газа по формуле:
см i x i
i 1

15.

где ωi – фактор ацентричности i-го компонента,
определяемый по формуле или из [1]:
i 0,4286
lg Pкр.i Pат
Т кр.i Tкип.i 1
1
где Ткип.i – температура кипения i-го компонента,
значение которой определяется из [1].
Псевдокритические параметры, необходимые для
определения Рпр и Тпр, с помощью которых из графиков
находят Z(0) и Z(1), должны быть определены в
зависимости от состава газа

16.

Рисунок 5 – Зависимость коэффициента сверхсжимаемости Z(0)
простых веществ от приведенных давления и температуры

17.

Рисунок 6 – Зависимость коэффициента сверхсжимаемости Z(1)
несферических молекул от приведенного давления и
температуры

18.

Кубические уравнения состояния
Для более точных расчетов Z должен быть
определен по кубическим уравнениям состояния
газов, наиболее широкое распространение, среди
которых получили уравнения Соаве, Редлиха-Квонга,
Пенга-Робинсона. При этих методах расчета
присутствие в газе кислых компонентов практически
не влияет на величину погрешности при определении
Z, если расчеты ведутся с учетом коэффициентов
взаимодействия.
Для определения коэффициента сверхсжимаемости
Z кубические уравнения состояния решаются
относительно Z.

19.

Уравнение
имеет вид:
состояния
Пенга-Робинсона
RT
a(T)
Р
v b v(v b) b(v b)
Для определения коэффициента
преобразуется к виду:
сверхсжимаемости
оно
Z
Z3 1 B Z2 A 3B2 2B Z (AB B2 B3 ) 0
Где
a кр
a(T) P ;
A 2 2
RT
0,45724 R 2Tкр2 ;
Ркр
bP ;
B
RT
a(T) a кр T ;
0,0778 RTкр ;
(Т) 1 m 1 T
b
Р кр
m 0,37464 1,54226 0,26992 2
R=8314 кДж/(кмоль*К)
(*)
0,5
пр
2

20.

Подставляя промежуточные ф-лы получаем:
А
В
2
0,45724 R 2Ткр
(Т) Р
Ркр R Т
2
2
0,0778 R Т кр Р
Р кр R Т
2
0,45724 (Т) Р Т кр
Ркр Т
0,0778 Р Т кр
Р кр Т
2
0,0778 Р пр
Т пр
0,45724 (Т) Р пр
2
Т пр

21.

Приведем уравнение (*) к виду:
f (Z) Z3 r Z2 s Z t 0
где r=-(1-В)=В-1; s=А-3В2-2В; t=-(АВ-В2-В3)=В2+В3-АВ
Корни кубического уравнения получаем методом Ньютона
(касательных). Для газа он соответствует максимальному
положительному. (В первом приближении можно принять
Z1=1 или 0,8).
f Zi
(1)
Z Z
i
Где
i 1
f Z Z r Z s Z t
3
2
f / Zi
f Z 3 Z 2 r Z s
/
2
(2)

22.

Приближения продолжаем до тех пор пока
величина f Zi не станет пренебрежимо
f / Zi
мала (например <0,0001).

23.

Уравнение состояния Редлиха-Квонга
Уравнение состояния Редлиха-Квонга имеет вид:
RT
a(T)
Р
0,5
v b Т v(v b)
Для определения коэффициента сверхсжимаемости Z оно
преобразуется к виду:
Z3 Z2 A* B*2 B* Z A*B* 0 (**)
A*
a P
R 2T 2,5
a
B*
b P
R T
(***)
0,42748 R 2Tкр2,5 b 0,08664 RTкр
Ркр
Р кр
(****)

24.

Подставляя ур-я (****) в (***)
А
*
В
*
2,5
0,42748 R 2 Ткр
Р
Ркр R Т
2
2,5
0,08664 R Р Т кр
R Р кр Т
0,42748 Рпр
2,5
Т пр
0,08664 Р пр
Т пр
Приведем ур-е (**) к виду:
Z3 r Z2 s Z t 0

25.

где r=-1; s=А*-В*2-В*; t=-А*∙В*
Корни кубического уравнения получаем методом
Ньютона по формулам (1) и (2).
Для газа он соответствует максимальному
положительному.