Похожие презентации:
Гидродинамика
1.
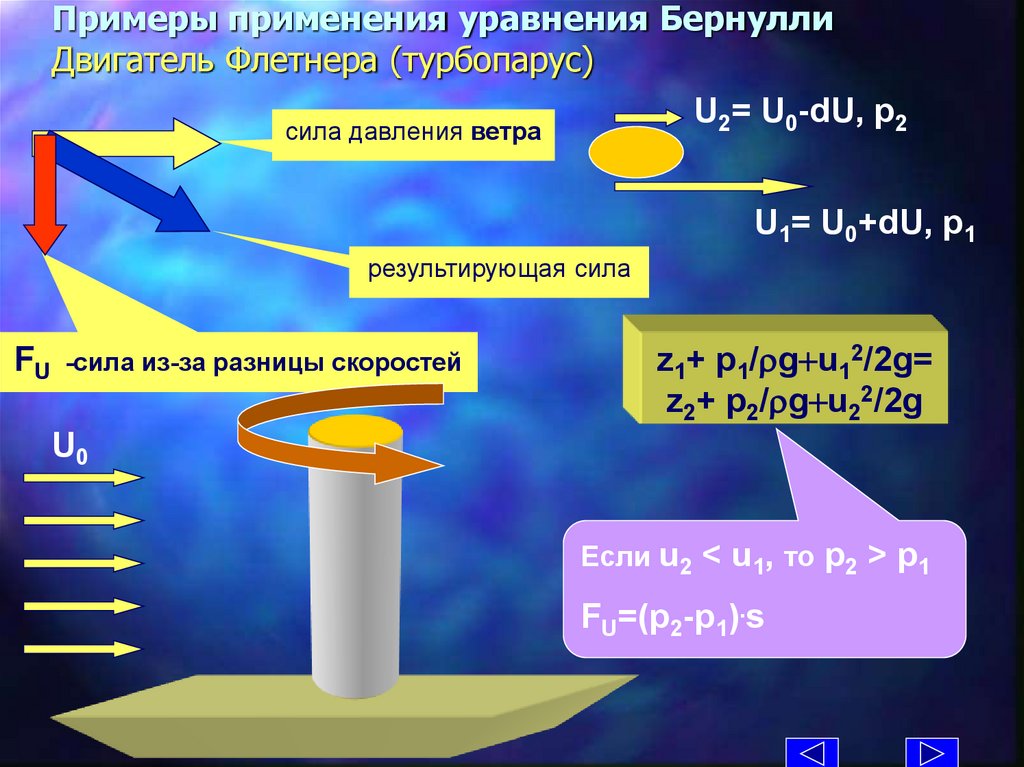
Примеры применения уравнения БернуллиДвигатель Флетнера (турбопарус)
U2= U0-dU, р2
сила давления ветра
U1= U0+dU, р1
результирующая сила
FU -сила из-за разницы скоростей
z1+ p1/rg+u12/2g=
z2+ p2/rg+u22/2g
U0
Если u2 < u1, то р2 > p1
FU=(p2-p1).s
2.
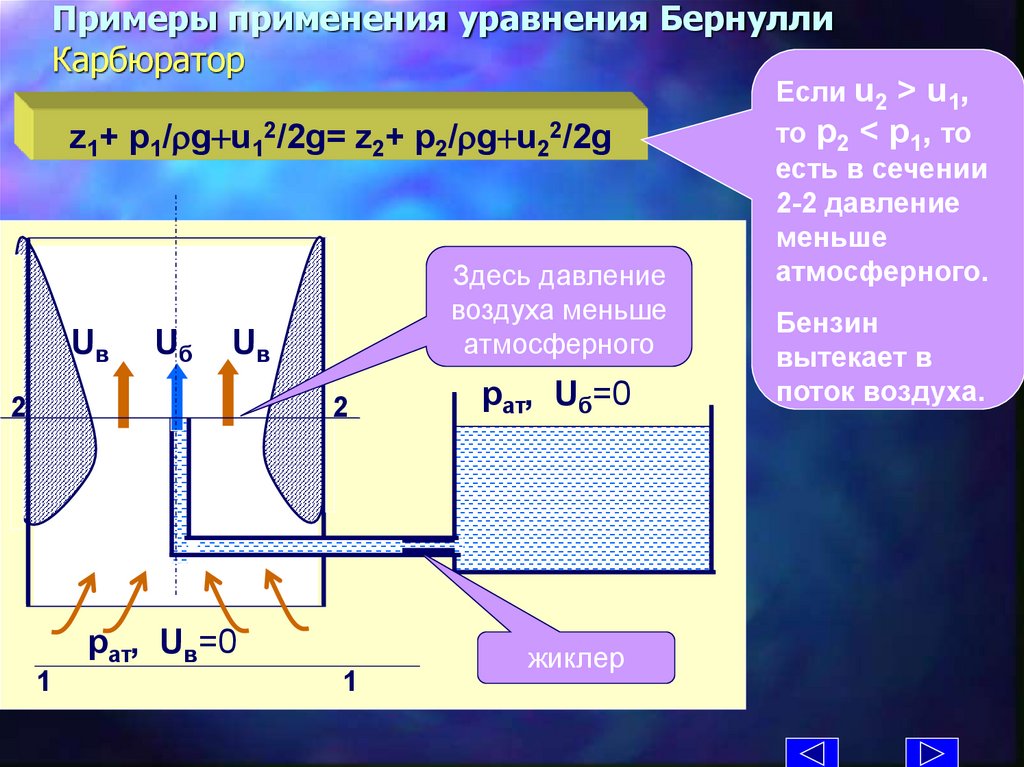
Примеры применения уравнения БернуллиКарбюратор
z1+ p1/rg+u12/2g= z2+ p2/rg+u22/2g
Uв
Uб
Здесь давление
воздуха меньше
атмосферного
Uв
2
2
рат, Uв=0
1
1
рат, Uб=0
жиклер
Если u2 > u1,
то р2 < p1, то
есть в сечении
2-2 давление
меньше
атмосферного.
Бензин
вытекает в
поток воздуха.
3.
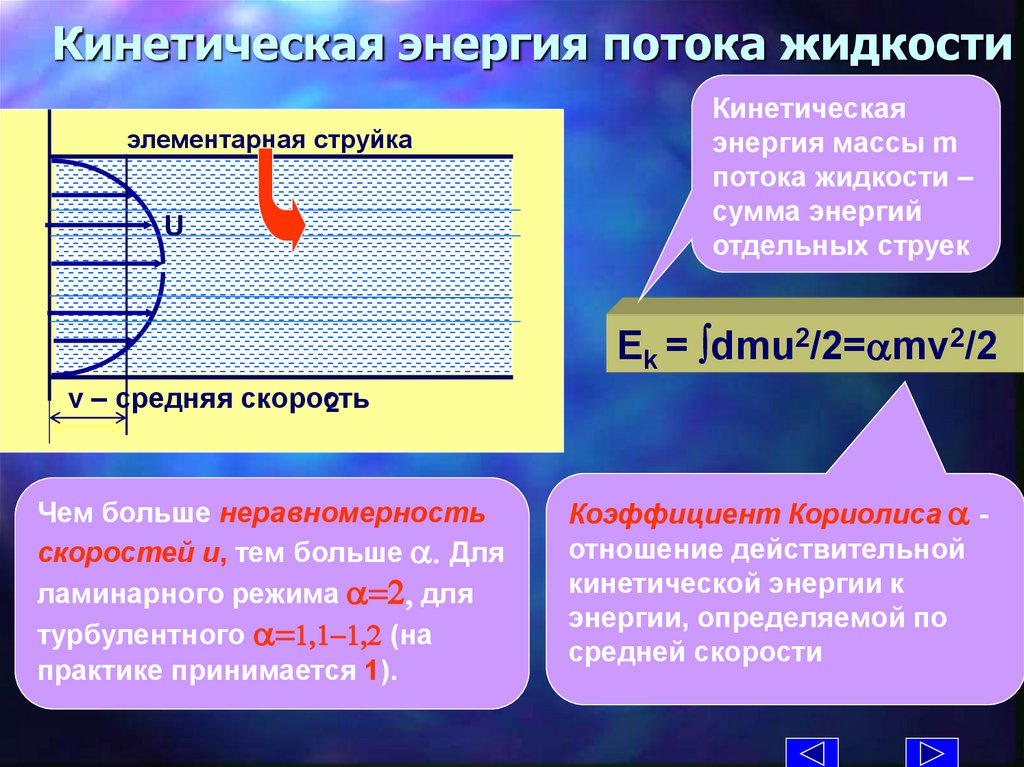
Кинетическая энергия потока жидкостиэлементарная струйка
U
2
U 2,
p2
v – средняя скорость
2
Чем больше неравномерность
скоростей u, тем больше a. Для
ламинарного режима a=2, для
турбулентного a=1,1-1,2 (на
практике принимается 1).
Кинетическая
энергия массы m
потока жидкости –
сумма энергий
отдельных струек
Ek = dmu2/2=amv2/2
Коэффициент Кориолиса a отношение действительной
кинетической энергии к
энергии, определяемой по
средней скорости
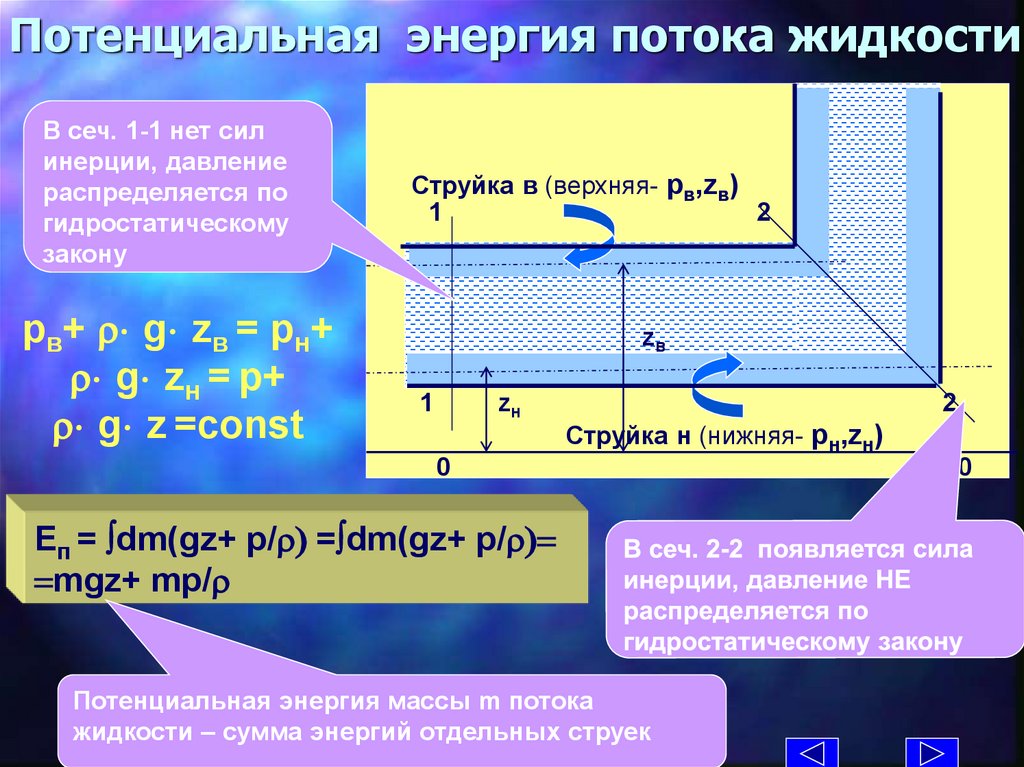
4.
Потенциальная энергия потока жидкостиВ сеч. 1-1 нет сил
инерции, давление
распределяется по
гидростатическому
закону
pв+ r g zв = pн+
r g zн = p+
r g z =const
Струйка в (верхняя- pв,zв)
1
2
zв
1
zн
2
Струйка н (нижняя- pн,zн)
0
Eп = dm(gz+ p/r) = dm(gz+ p/r)=
=mgz+ mp/r
Потенциальная энергия массы m потока
жидкости – сумма энергий отдельных струек
0
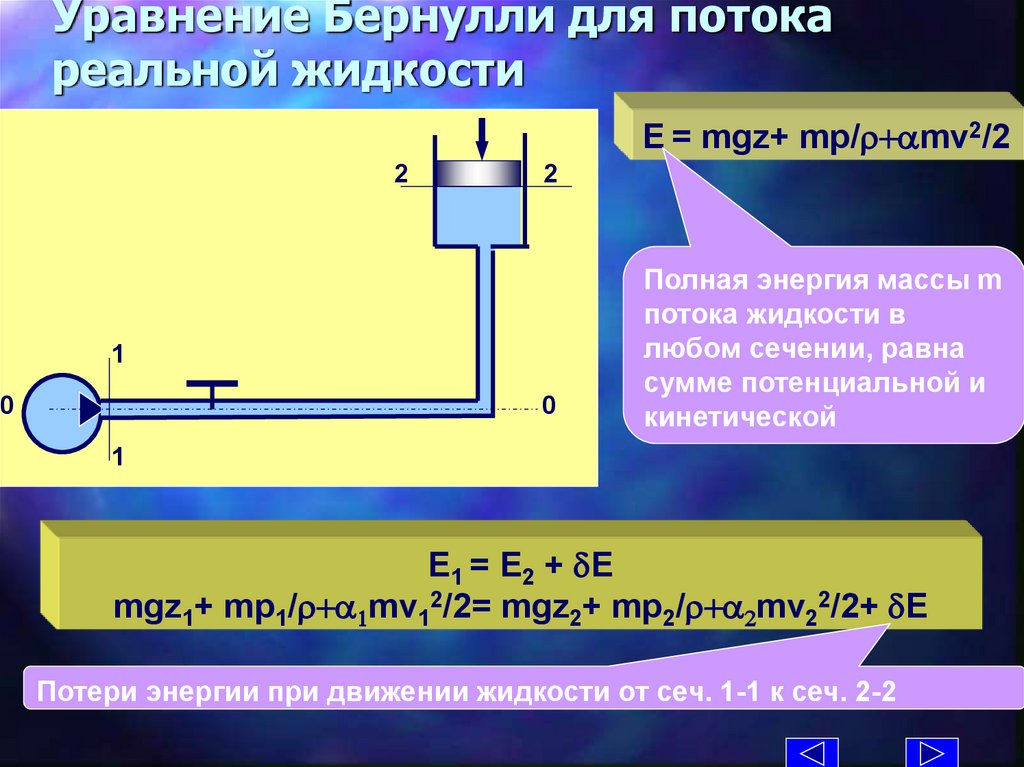
5.
Уравнение Бернулли для потокареальной жидкости
E = mgz+ mp/r+amv2/2
2
2
1
0
0
Полная энергия массы m
потока жидкости в
любом сечении, равна
сумме потенциальной и
кинетической
1
E1 = E2 + dE
mgz1+ mp1/r+a1mv12/2= mgz2+ mp2/r+a2mv22/2+ dE
Потери энергии при движении жидкости от сеч. 1-1 к сеч. 2-2
6.
Удельная энергияE = mgz+ mp/r+amv2/2
Полная энергия,
джоули (Н*м)
УДЕЛЬНАЯ - энергия, отнесенная к количеству
вещества (объёмному, или массовому, или весовому)
E/G =E/mg = z+ p/rg+av2/2g=H
Гидродинамический напор – энергия единицы веса,
метры
E/W =E/(m/r) = rgz+ p+arv2/2
Полное давление – энергия единицы объёма, Па
7.
НапорЭто энергия, отнесенная к весу жидкости
Измеряется в метрах
Используется для построения графиков изменения
различных видов энергии по длине потока
z1+ p1/rg+a1v12/2g= z2+ p2/rg+a2v22/2g+ h1-2
Напор
Потери напора на
преодоление
сопротивлений
геометрический
скоростной
z 1, z 2
v12/2g , v22/2g
пьезометрический
р1/rg, р2/rg
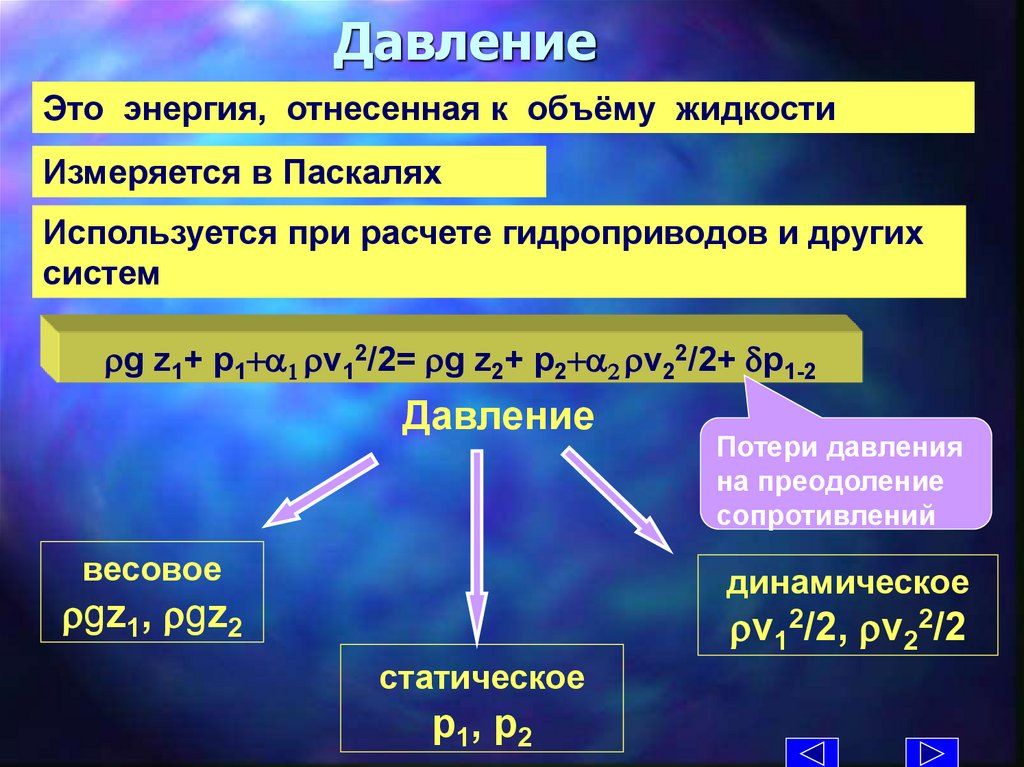
8.
ДавлениеЭто энергия, отнесенная к объёму жидкости
Измеряется в Паскалях
Используется при расчете гидроприводов и других
систем
rg z1+ p1+a1 rv12/2= rg z2+ p2+a2 rv22/2+ dp1-2
Давление
весовое
Потери давления
на преодоление
сопротивлений
динамическое
rgz1, rgz2
rv12/2, rv22/2
статическое
р1, р2
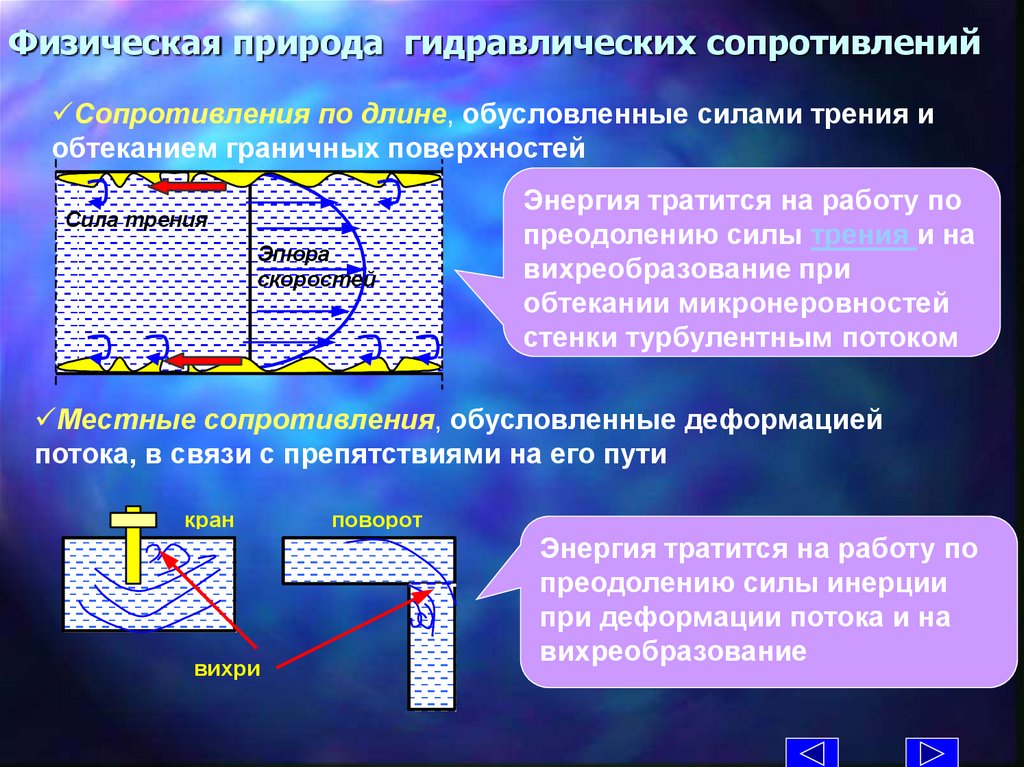
9.
Физическая природа гидравлических сопротивленийСопротивления по длине, обусловленные силами трения и
обтеканием граничных поверхностей
Сила трения
Эпюра
скоростей
Энергия тратится на работу по
преодолению силы трения и на
вихреобразование при
обтекании микронеровностей
стенки турбулентным потоком
Местные сопротивления, обусловленные деформацией
потока, в связи с препятствиями на его пути
кран
вихри
поворот
Энергия тратится на работу по
преодолению силы инерции
при деформации потока и на
вихреобразование
10.
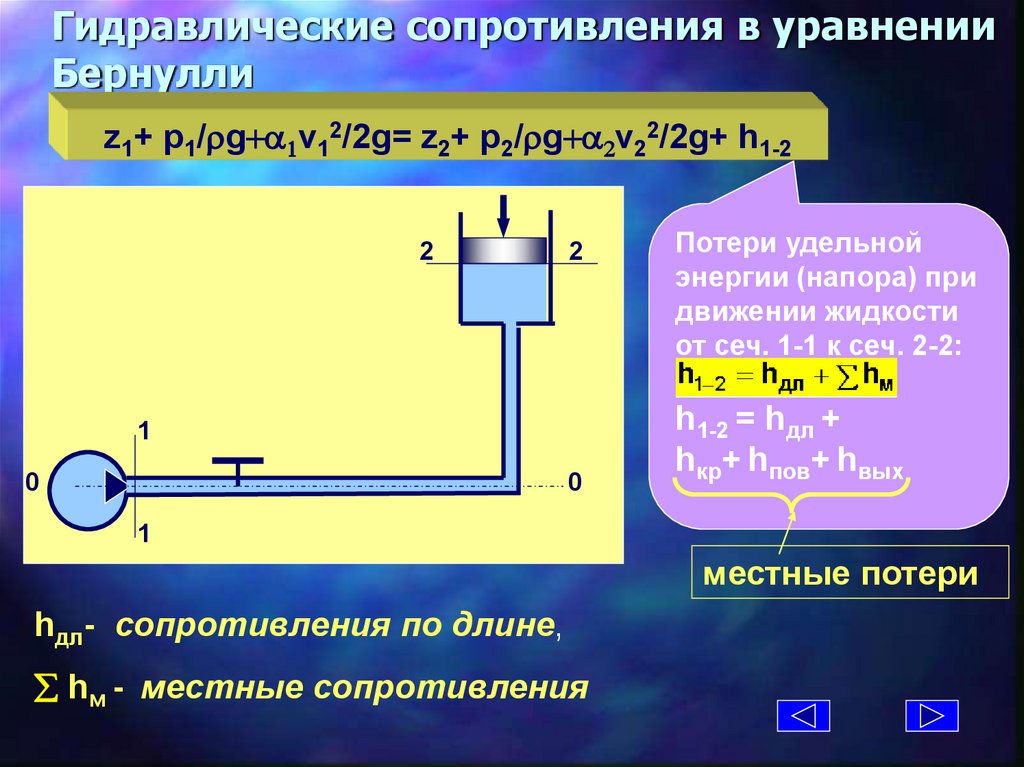
Гидравлические сопротивления в уравненииБернулли
z1+ p1/rg+a1v12/2g= z2+ p2/rg+a2v22/2g+ h1-2
2
2
1
0
0
Потери удельной
энергии (напора) при
движении жидкости
от сеч. 1-1 к сеч. 2-2:
h1-2 = hдл +
hкр+ hпов+ hвых
1
местные потери
hдл- cопротивления по длине,
hм - местные сопротивления
11.
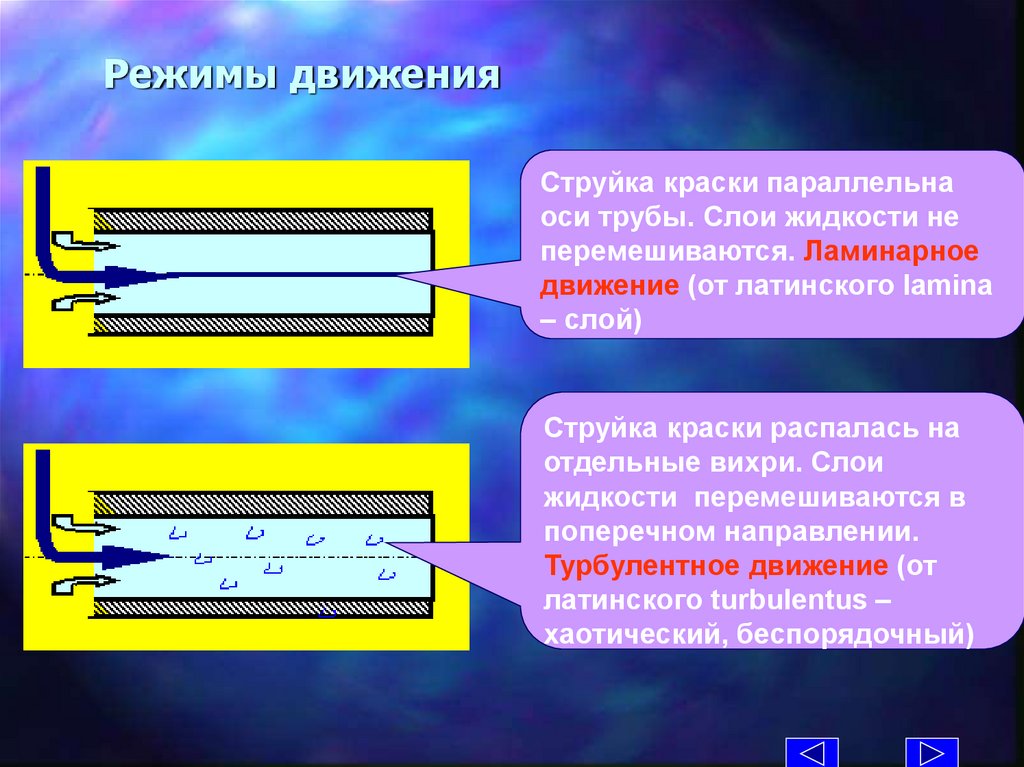
Режимы движенияСтруйка краски параллельна
оси трубы. Слои жидкости не
перемешиваются. Ламинарное
движение (от латинского lamina
– слой)
Струйка краски распалась на
отдельные вихри. Слои
жидкости перемешиваются в
поперечном направлении.
Турбулентное движение (от
латинского turbulentus –
хаотический, беспорядочный)
12.
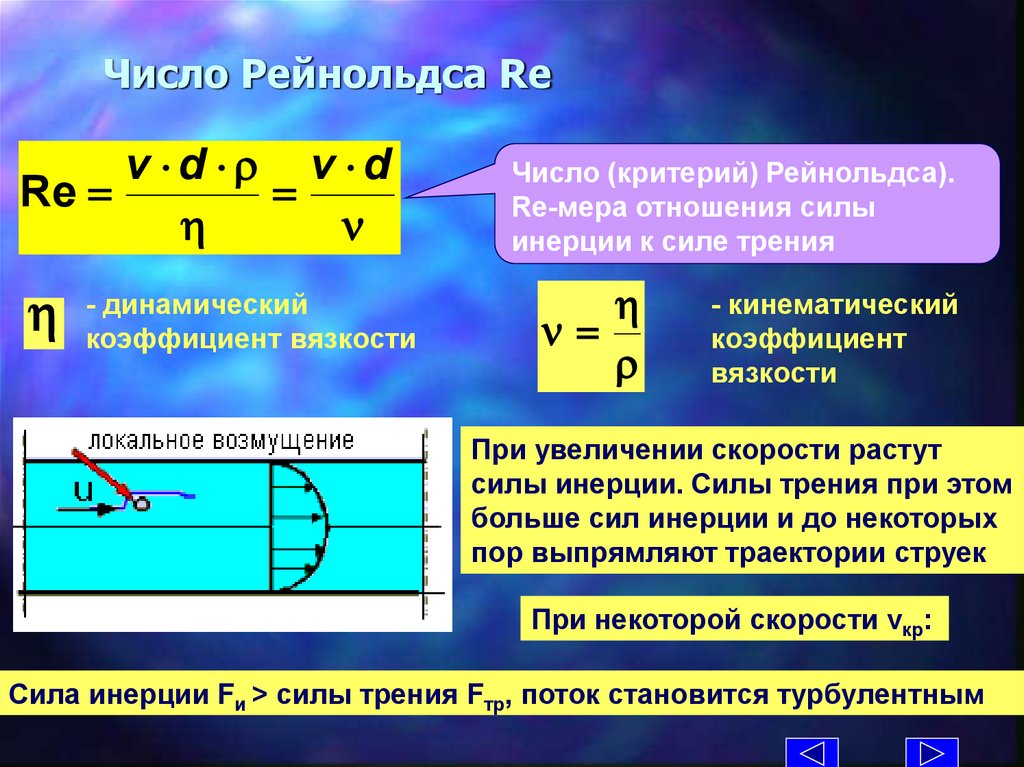
Число Рейнольдса Rev d r v d
Re =
=
динамический
-коэффициент
вязкости
Число (критерий) Рейнольдса).
Re-мера отношения силы
инерции к силе трения
=
r
- кинематический
коэффициент
вязкости
При увеличении скорости растут
силы инерции. Силы трения при этом
больше сил инерции и до некоторых
пор выпрямляют траектории струек
При некоторой скорости vкр:
Сила инерции Fи > силы трения Fтр, поток становится турбулентным
13.
Критическое число Рейнольдса ReкрReкр
Число Рейнольдса, при котором ламинарный
режим сменяется турбулентным
Reкр зависит от формы сечения канала
- в таком канале больше
поверхность контакта
между жидкостью и
стенкой и больше
локальных
возмущающих факторов
Reкр =2300
Reкр =1600
14.
Гидравлический диаметрХарактерный линейный размер сечения.
4s
dг =
S - площадь сечения; П - смоченный периметр
- по этой формуле определяется
v dг r v dг
Re =
=
число Рейнольдса в канале любой
геометрии
4s 4 d 2
dг =
=
=d
4 d
4s 4 d 2 2
dг = =
=d
8 d
4s 4 (D 2 - d 2 )
dг =
=
= D -d
4 (D + d )
15.
Потери по длине.Формула Дарси-Вейсбаха
2
l v
hдл =
d 2g
Формула Дарси-Вейсбаха
- коэффициент гидравлического трения,
зависит от режима движения и состояния
поверхности трубопровода
l, d – длина и диаметр трубопровода
v – средняя скорость движения
16.
Местные потери. Формула Вейсбаха2
v
hм =
2g
Формула Вейсбаха
- коэффициент местного сопротивления,
зависит от его вида и конструктивного
выполнения
– приводится в справочной литературе
v – средняя скорость движения
17.
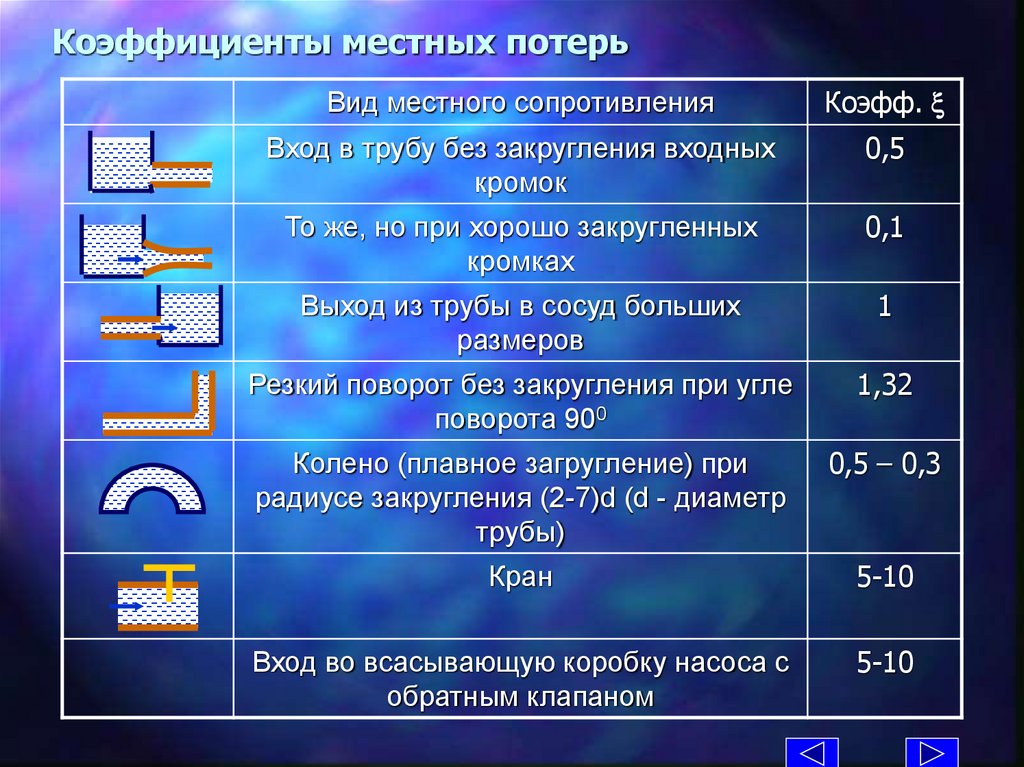
Коэффициенты местных потерьВид местного сопротивления
Коэфф.
Вход в трубу без закругления входных
кромок
0,5
То же, но при хорошо закругленных
кромках
0,1
Выход из трубы в сосуд больших
размеров
1
Резкий поворот без закругления при угле
поворота 900
1,32
Колено (плавное загругление) при
радиусе закругления (2-7)d (d - диаметр
трубы)
0,5 – 0,3
Кран
5-10
Вход во всасывающую коробку насоса с
обратным клапаном
5-10
18.
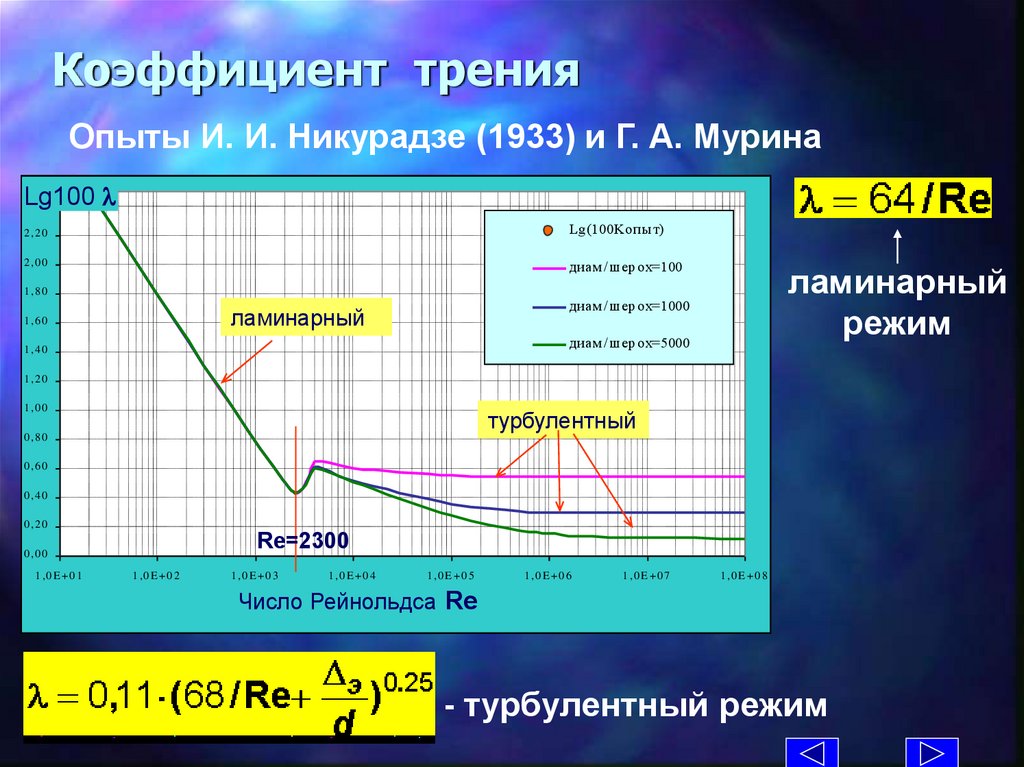
Коэффициент тренияОпыты И. И. Никурадзе (1933) и Г. А. Мурина
Lg100
2 ,4 0
2 ,2 0
Lg (100Kо пы т)
2 ,0 0
диам /ш ер о х=100
ламинарный
режим
1 ,8 0
диам /ш ер о х=1000
ламинарный
1 ,6 0
диам /ш ер о х=5000
1 ,4 0
1 ,2 0
1 ,0 0
турбулентный
0 ,8 0
0 ,6 0
0 ,4 0
0 ,2 0
Re=2300
0 ,0 0
1 ,0 E +0 1
1 ,0 E +0 2
1 ,0 E +0 3
1 ,0 E +0 4
1 ,0 E +0 5
1 ,0 E +0 6
1 ,0 E +0 7
1 ,0 E +0 8
Ч и с ло Р е й н о льдсRe
а
Число Рейнольдса
- турбулентный режим
19.
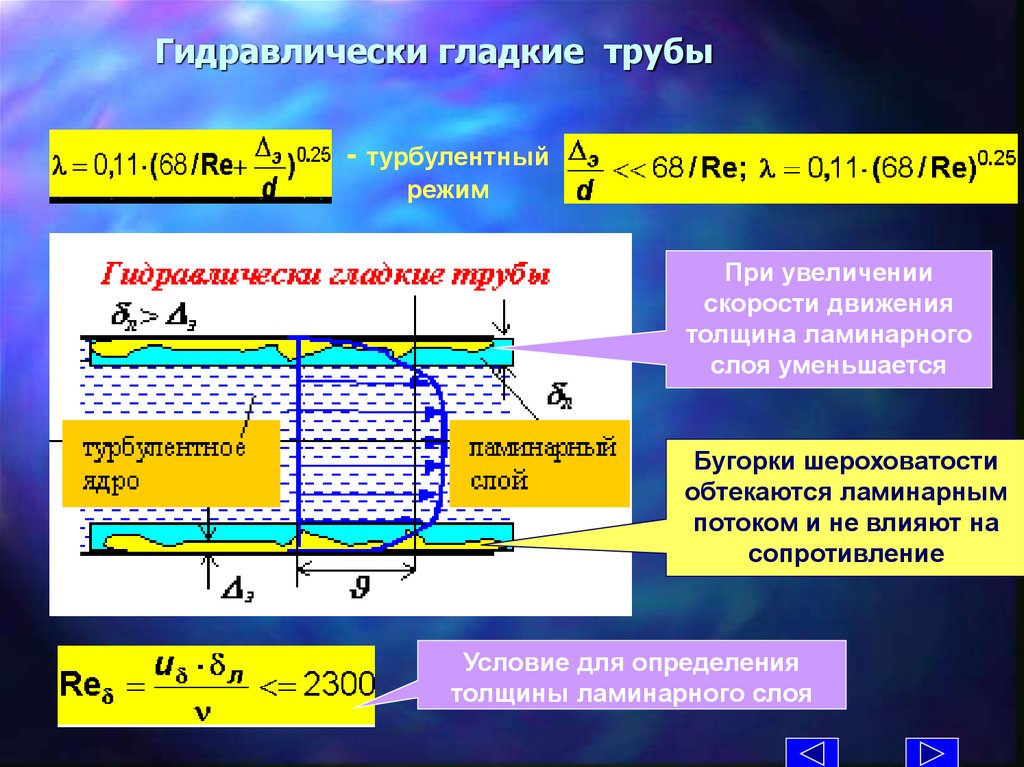
Гидравлически гладкие трубы- турбулентный
режим
При увеличении
скорости движения
толщина ламинарного
слоя уменьшается
Бугорки шероховатости
обтекаются ламинарным
потоком и не влияют на
сопротивление
Условие для определения
толщины ламинарного слоя
20.
Гидравлически шероховатые трубыПри увеличении скорости толщина ламинарного слоя уменьшается
Бугорки шероховатости
выступают в турбулентное ядро,
с них срываются вихри. А это
дополнительное сопротивление
При дальнейшем увеличении скорости
Ламинарный слой очень тонкий. Все
бугорки шероховатости выступают в
турбулентное ядро и полностью
определяют сопротивление трубы.
21.
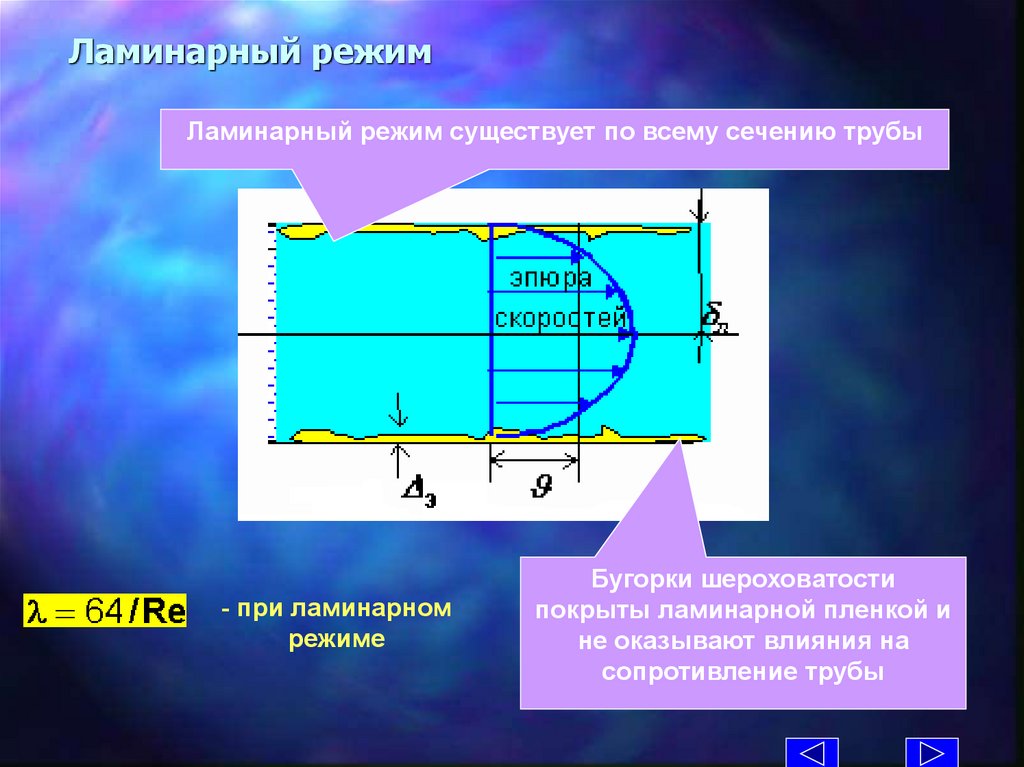
Ламинарный режимЛаминарный режим существует по всему сечению трубы
- при ламинарном
режиме
Бугорки шероховатости
покрыты ламинарной пленкой и
не оказывают влияния на
сопротивление трубы
22.
Рекомендации для расчетов- при ламинарном режиме
- при турбулентном
режиме
При проведении расчетов то слагаемое,
которое несущественно, дает незначительный
вклад в величину коэффициента трения
23.
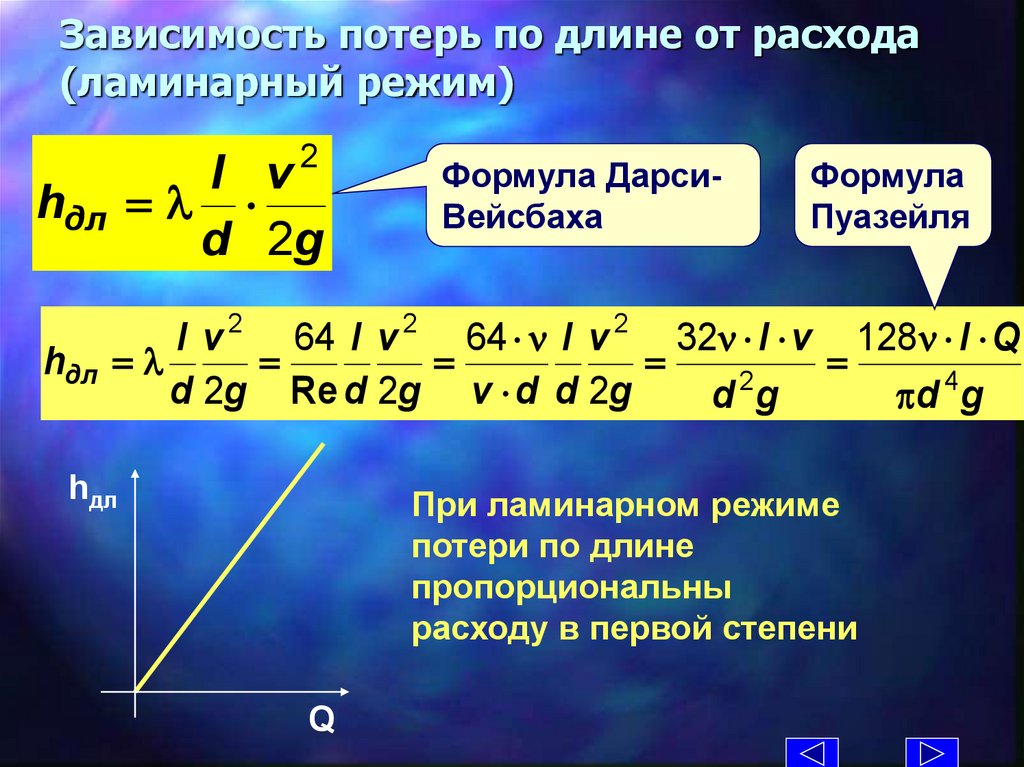
Зависимость потерь по длине от расхода(ламинарный режим)
2
l v
hдл =
d 2g
Формула ДарсиВейсбаха
Формула
Пуазейля
l v 2 64 l v 2 64 l v 2 32 l v 128 l Q
hдл =
=
=
=
=
2
d 2g Re d 2g v d d 2g
d g
d 4 g
hдл
При ламинарном режиме
потери по длине
пропорциональны
расходу в первой степени
Q
24.
Зависимость потерь по длине от расхода(турбулентный режим)
l v2
hдл =
d 2g
Формула ДарсиВейсбаха
68 э 0,2
= 0,11 (
+
)
v d d
lv
68 0,25 l v
hдл =
= 0,11 (
)
v 1.75 Q1.75
d 2g
v d
d 2g
2
2
э 0,25 l v 2
l v2
hдл =
= 0,11 ( )
v 2 Q2
d 2g
d
d 2g
Гидравлически
гладкие трубы
Абсолютно
шероховатые
трубы
hдл
При турбулентном режиме
потери по длине
пропорциональны Q 1.75-2
Q0
Q









 Физика
Физика