Похожие презентации:
Гидродинамика. Движение жидкости
1.
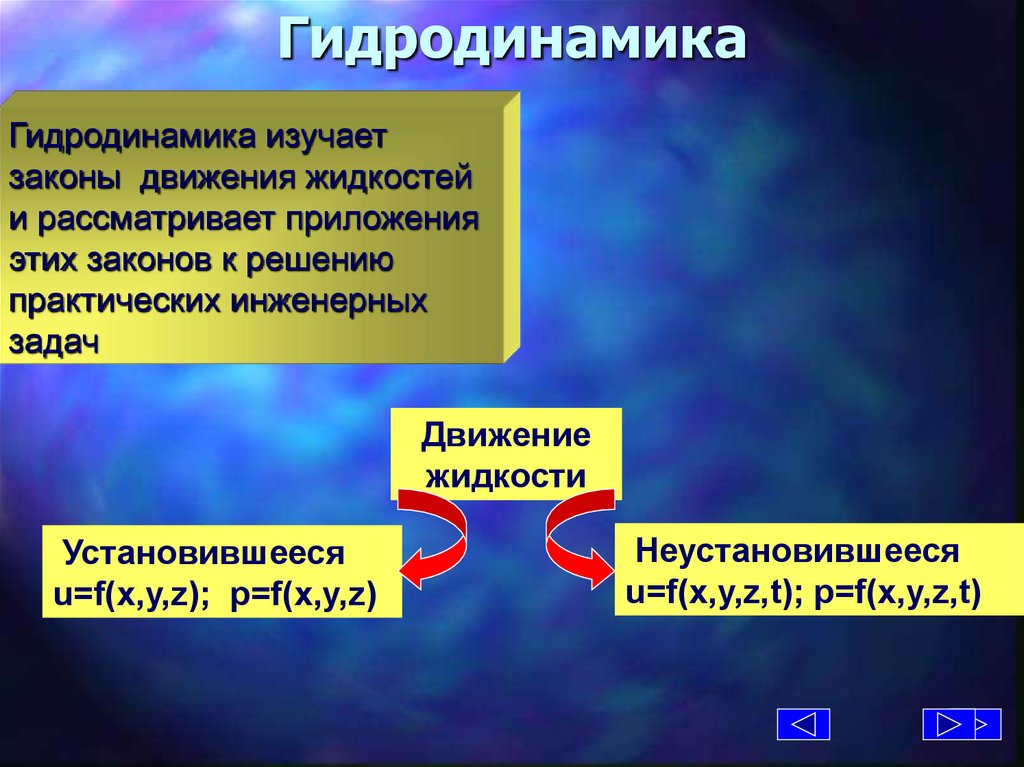
ГидродинамикаГидродинамика изучает
законы движения жидкостей
и рассматривает приложения
этих законов к решению
практических инженерных
задач
Движение
жидкости
Установившееся
u=f(x,y,z); p=f(x,y,z)
Неустановившееся
u=f(x,y,z,t); p=f(x,y,z,t)
2.
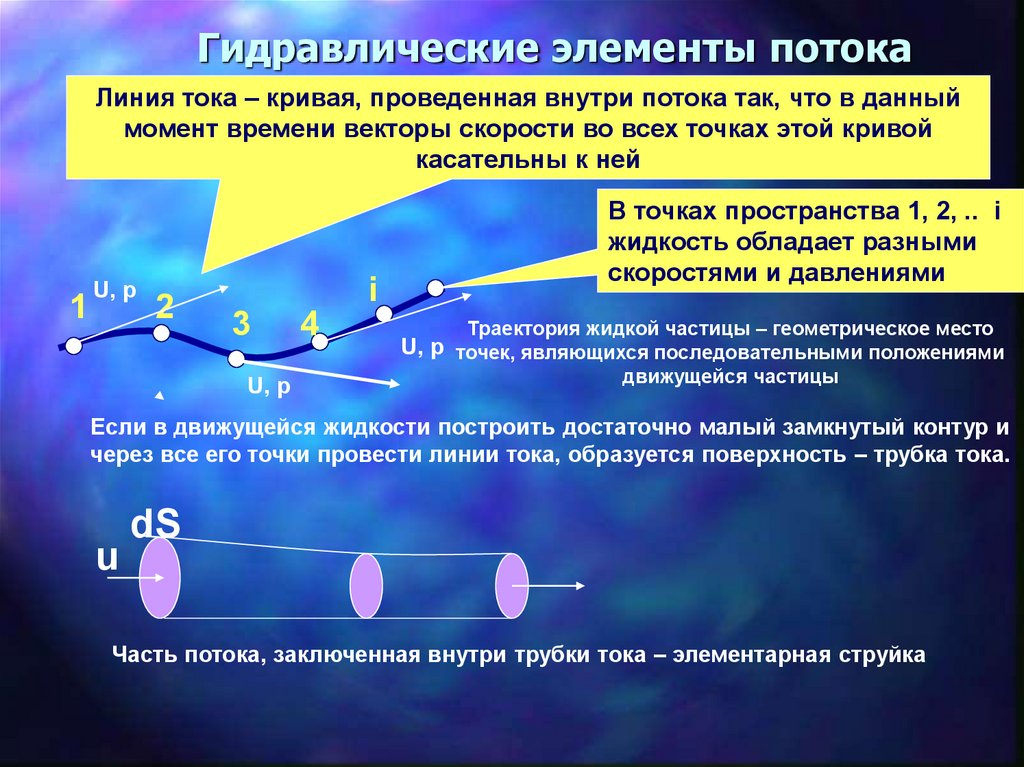
Гидравлические элементы потокаЛиния тока – кривая, проведенная внутри потока так, что в данный
момент времени векторы скорости во всех точках этой кривой
касательны к ней
1
U, p
2
i
3
U, p
4
В точках пространства 1, 2, .. i
жидкость обладает разными
скоростями и давлениями
Траектория жидкой частицы – геометрическое место
U, p точек, являющихся последовательными положениями
движущейся частицы
Если в движущейся жидкости построить достаточно малый замкнутый контур и
через все его точки провести линии тока, образуется поверхность – трубка тока.
u
dS
Часть потока, заключенная внутри трубки тока – элементарная струйка
3.
Элементарная струйка и поток жидкостиЭлементарная струйка, скорость U, сечение ds
U
живое
(поперечное)
сечение (s)
Поток жидкости – совокупность элементарных струек,
движущихся с разными скоростями
Живое (поперечное) сечение – сечение,
перпендикулярное направлению скоростей
Для напорного течения:
S=pd2/4 -площадь сечения P=pd -смоченный периметр
4.
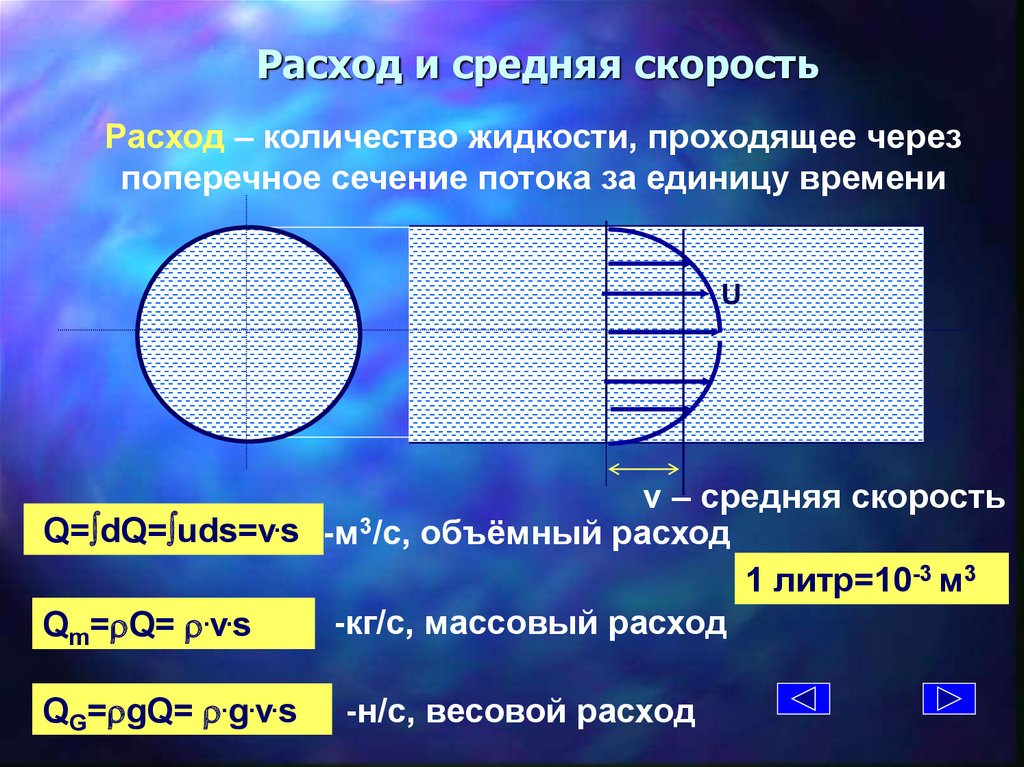
Расход и средняя скоростьРасход – количество жидкости, проходящее через
поперечное сечение потока за единицу времени
U
v – средняя скорость
Q= dQ= uds=v.s -м3/с, объёмный расход
1 литр=10-3 м3
-кг/c, массовый расход
Qm=rQ= r.v.s
QG=rgQ= r.g.v.s
-н/c, весовой расход
5.
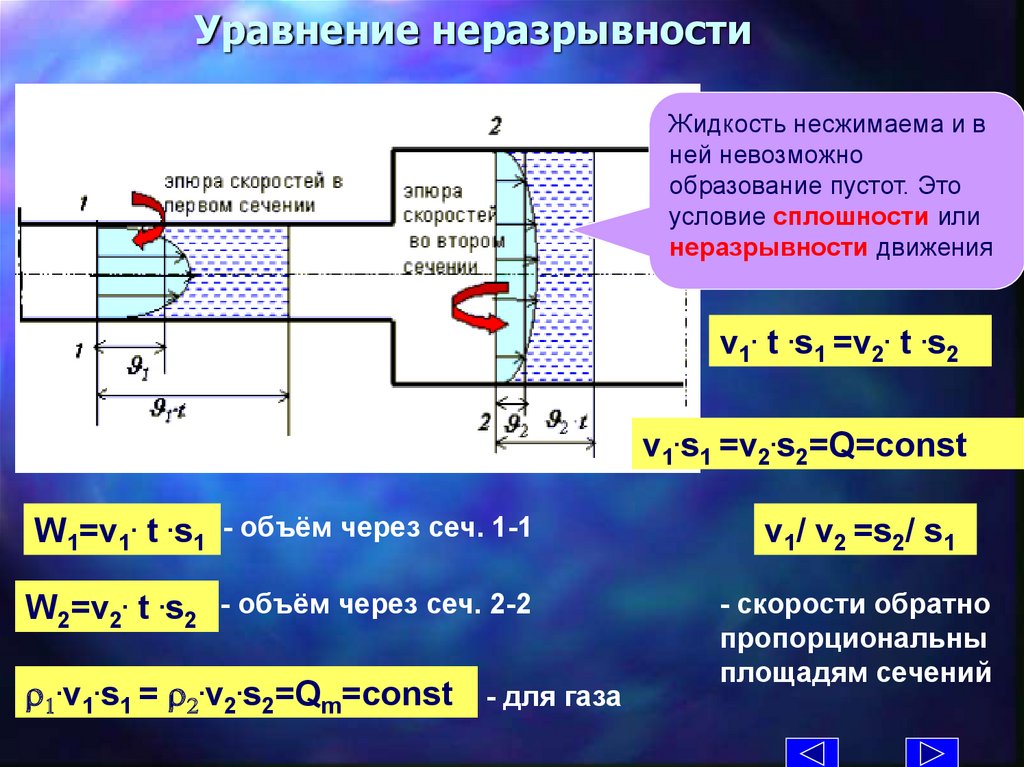
Уравнение неразрывностиЖидкость несжимаема и в
ней невозможно
образование пустот. Это
условие сплошности или
неразрывности движения
v1. t .s1 =v2. t .s2
v1.s1 =v2.s2=Q=const
W1=v1. t .s1 - объём через сеч. 1-1
v1/ v2 =s2/ s1
W2=v2. t .s2 - объём через сеч. 2-2
- скорости обратно
пропорциональны
площадям сечений
r1.v1.s1 = r2.v2.s2=Qm=const - для газа
6.
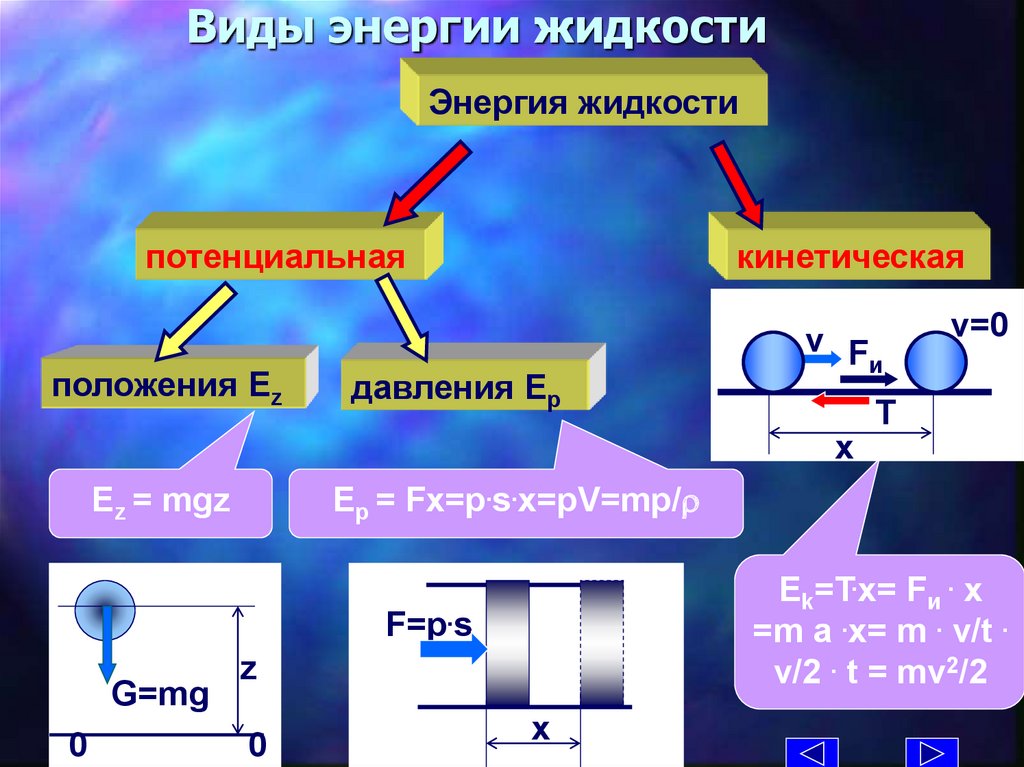
Виды энергии жидкостиЭнергия жидкости
потенциальная
положения Ez
кинетическая
давления Ep
v F
и
v=0
T
x
Ep = Fx=p.s.x=pV=mp/r
Ez = mgz
Ek=T.x= Fи . x
=m a .x= m . v/t .
v/2 . t = mv2/2
F=p.s
G=mg
0
z
0
x
7.
Закон сохранения энергии – уравнение Бернулли1. Идеальная жидкость, элементарная струйка
U 2,
2
p2
2
E = dmgz+ dmp/r+dmu2/2
полная энергия массы dm жидкости
z2
1
E1 = E2
dmgz1+ dmp1/r+dmu12/2=
dmgz2+ dmp2/r+dmu22/2
1
U1, p1
0
z1
0
z1+ p1/ +u12/2g= z2+ p2/ +u22/2g
При движении идеальной жидкости
полная энергия сохраняется.
Возможен переход одного вида
энергии в другой
Уравнение Бернулли
(1738)
8.
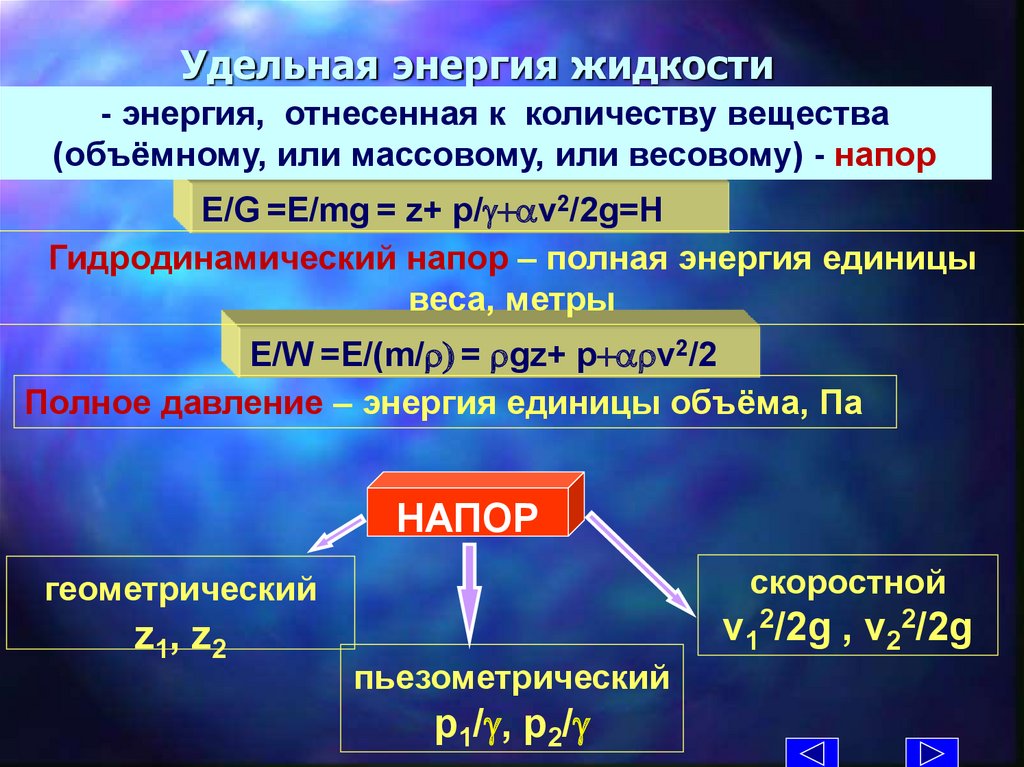
Удельная энергия жидкости- энергия, отнесенная к количеству вещества
(объёмному, или массовому, или весовому) - напор
E/G =E/mg = z+ p/ +av2/2g=H
Гидродинамический напор – полная энергия единицы
веса, метры
E/W =E/(m/r) = rgz+ p+arv2/2
Полное давление – энергия единицы объёма, Па
НАПОР
геометрический
скоростной
z 1, z 2
v12/2g , v22/2g
пьезометрический
р1/ , р2/
9.
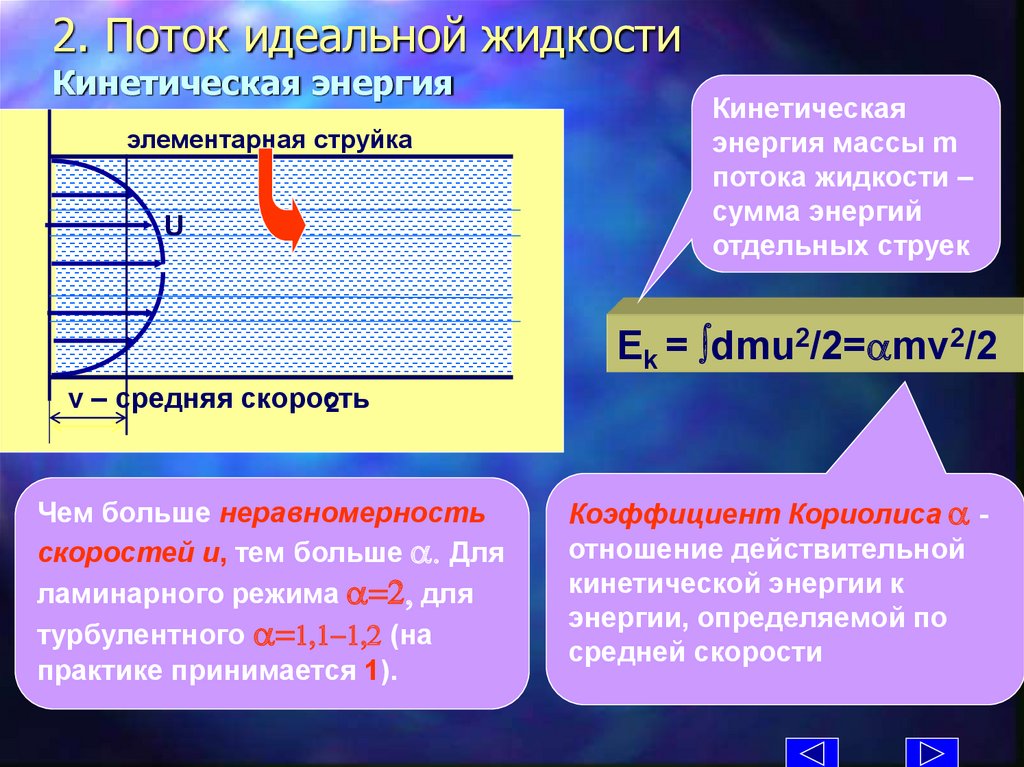
2. Поток идеальной жидкостиКинетическая энергия
элементарная струйка
U
2
U 2,
p2
v – средняя скорость
2
Чем больше неравномерность
скоростей u, тем больше a. Для
ламинарного режима a=2, для
турбулентного a=1,1-1,2 (на
практике принимается 1).
Кинетическая
энергия массы m
потока жидкости –
сумма энергий
отдельных струек
Ek = dmu2/2=amv2/2
Коэффициент Кориолиса a отношение действительной
кинетической энергии к
энергии, определяемой по
средней скорости
10.
Потенциальная энергияВ сеч. 1-1 нет сил
инерции, давление
распределяется по
гидростатическому
закону
pв+ r g zв = pн+
r g zн = p+
r g z =const
Струйка в (верхняя- pв,zв)
1
2
zв
1
zн
2
Струйка н (нижняя- pн,zн)
0
Eп = dm(gz+ p/r) = dm(gz+ p/r)=
=mgz+ mp/r
Потенциальная энергия массы m потока
жидкости – сумма энергий отдельных струек
0
11.
Полная энергия:E = mgz+ mp/r+amv2/2 = const
m=const, r = const:
z1 +
p1
+
av
2
1
2g
= z2 +
p2
+
av
2
2
2g
уравнение
- Бернулли для потока
идеальной жидкости
12.
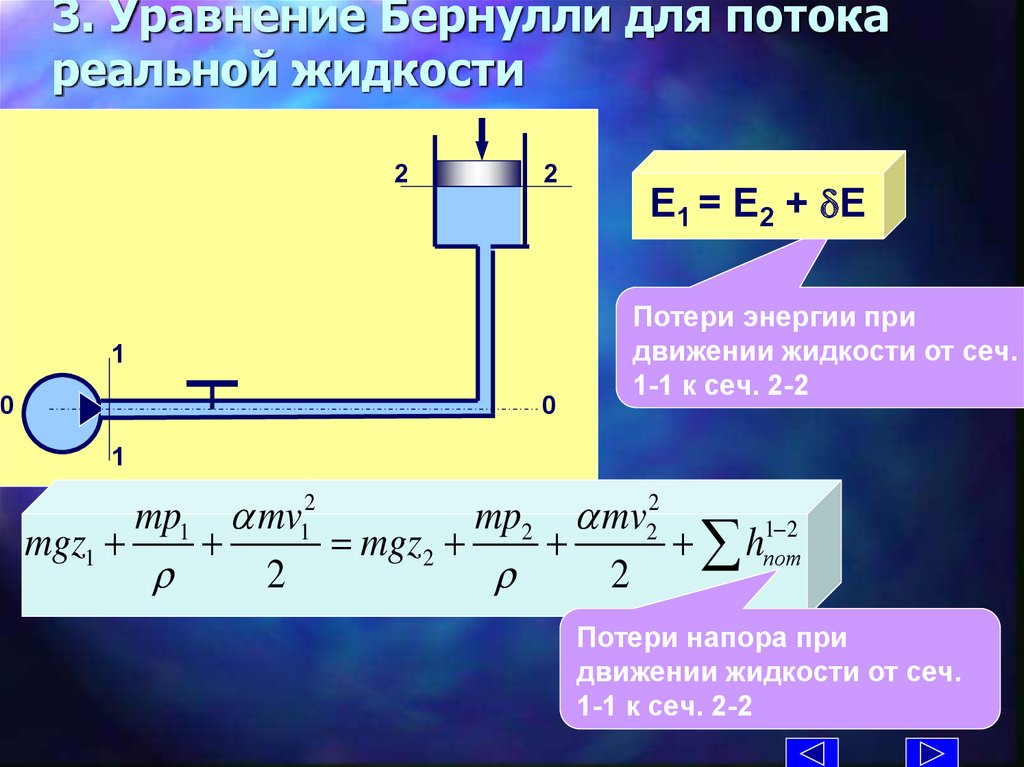
3. Уравнение Бернулли для потокареальной жидкости
2
2
1
0
0
E1 = E2 + dE
Потери энергии при
движении жидкости от сеч.
1-1 к сеч. 2-2
1
mp1 a mv12
mp2 a mv22
1- 2
mgz1 +
+
= mgz2 +
+
+ hпот
r
2
r
2
Потери напора при
движении жидкости от сеч.
1-1 к сеч. 2-2
13.
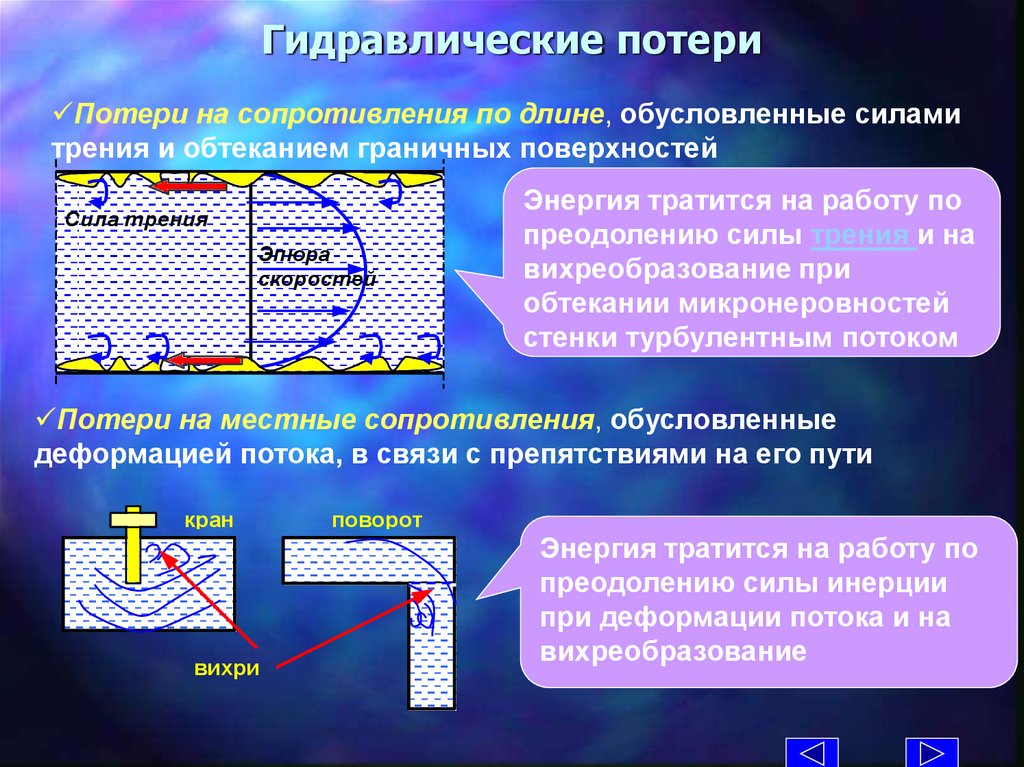
Гидравлические потериПотери на сопротивления по длине, обусловленные силами
трения и обтеканием граничных поверхностей
Сила трения
Эпюра
скоростей
Энергия тратится на работу по
преодолению силы трения и на
вихреобразование при
обтекании микронеровностей
стенки турбулентным потоком
Потери на местные сопротивления, обусловленные
деформацией потока, в связи с препятствиями на его пути
кран
вихри
поворот
Энергия тратится на работу по
преодолению силы инерции
при деформации потока и на
вихреобразование
14.
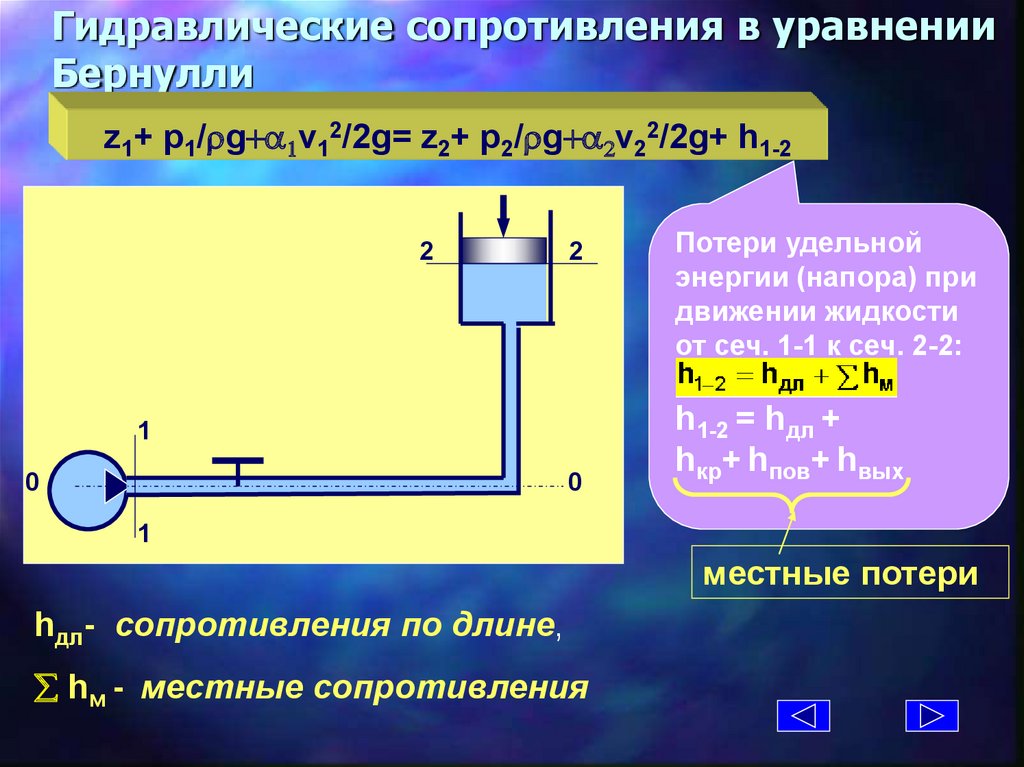
Гидравлические сопротивления в уравненииБернулли
z1+ p1/rg+a1v12/2g= z2+ p2/rg+a2v22/2g+ h1-2
2
2
1
0
0
Потери удельной
энергии (напора) при
движении жидкости
от сеч. 1-1 к сеч. 2-2:
h1-2 = hдл +
hкр+ hпов+ hвых
1
местные потери
hдл- cопротивления по длине,
hм - местные сопротивления
15.
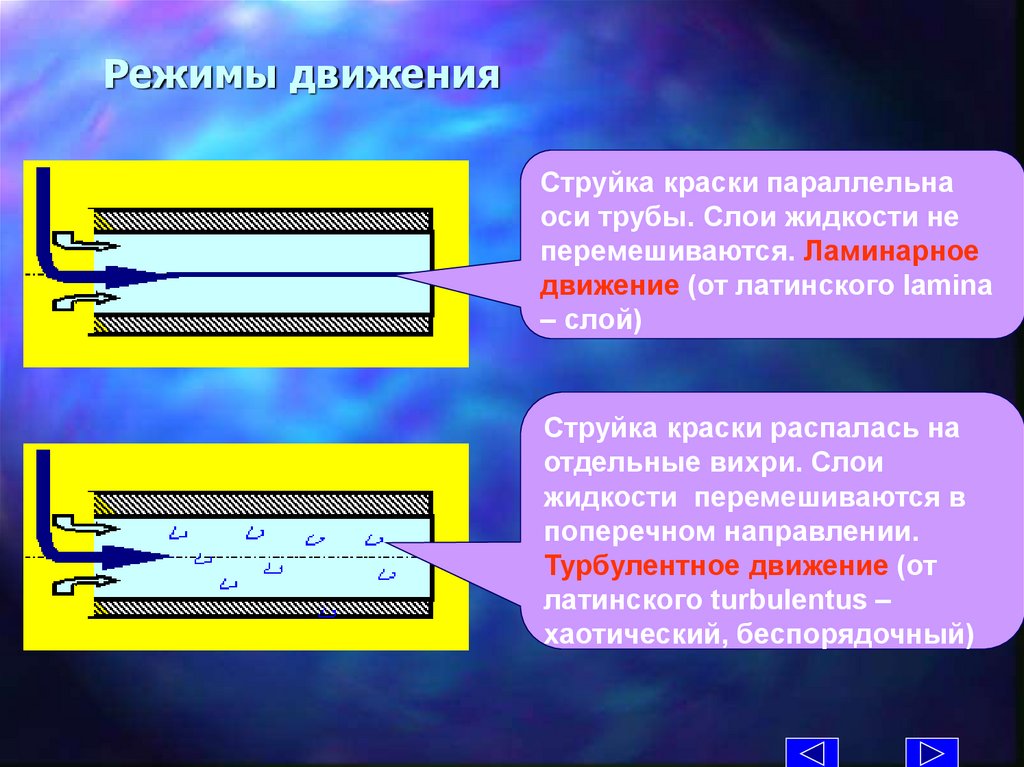
Режимы движенияСтруйка краски параллельна
оси трубы. Слои жидкости не
перемешиваются. Ламинарное
движение (от латинского lamina
– слой)
Струйка краски распалась на
отдельные вихри. Слои
жидкости перемешиваются в
поперечном направлении.
Турбулентное движение (от
латинского turbulentus –
хаотический, беспорядочный)
16.
Число Рейнольдса ReRe = v d r = v d
- динамический
коэффициент вязкости
Число (критерий) Рейнольдса).
Re-мера отношения силы
инерции к силе трения
=r
- кинематический
коэффициент
вязкости
При увеличении скорости растут
силы инерции. Силы трения при этом
больше сил инерции и до некоторых
пор выпрямляют траектории струек
При некоторой скорости vкр:
Сила инерции Fи > силы трения Fтр, поток становится турбулентным
17.
Критическое число Рейнольдса ReкрReкр
Число Рейнольдса, при котором ламинарный
режим сменяется турбулентным
Reкр зависит от формы сечения канала
- в таком канале больше
поверхность контакта
между жидкостью и
стенкой и больше
локальных
возмущающих факторов
Reкр =2300
Reкр =1600
18.
Гидравлический диаметр4s
dг =
P
Характерный линейный размер сечения.
S - площадь сечения; П - смоченный периметр
v dг r v dг
Re = =
- по этой формуле определяется
число Рейнольдса в канале любой
геометрии
4 s 4 pd 2
dг =
=
=d
P 4 pd
4 s 4 pd 2 2
dг =
=
=d
P
8 pd
4s 4p(D 2 - d 2 )
dг =
=
= D -d
P
4 p(D + d )
19.
Потери по длине.Формула Дарси-Вейсбаха
2
hдл
l v
=
d 2g
Формула Дарси-Вейсбаха
- коэффициент гидравлического трения,
зависит от режима движения и состояния
поверхности трубопровода
l, d – длина и диаметр трубопровода
v – средняя скорость движения
20.
Местные потери. Формула Вейсбаха2
v
hм =
2g
Формула Вейсбаха
- коэффициент местного сопротивления,
зависит от его вида и конструктивного
выполнения
– приводится в справочной литературе
v – средняя скорость движения
21.
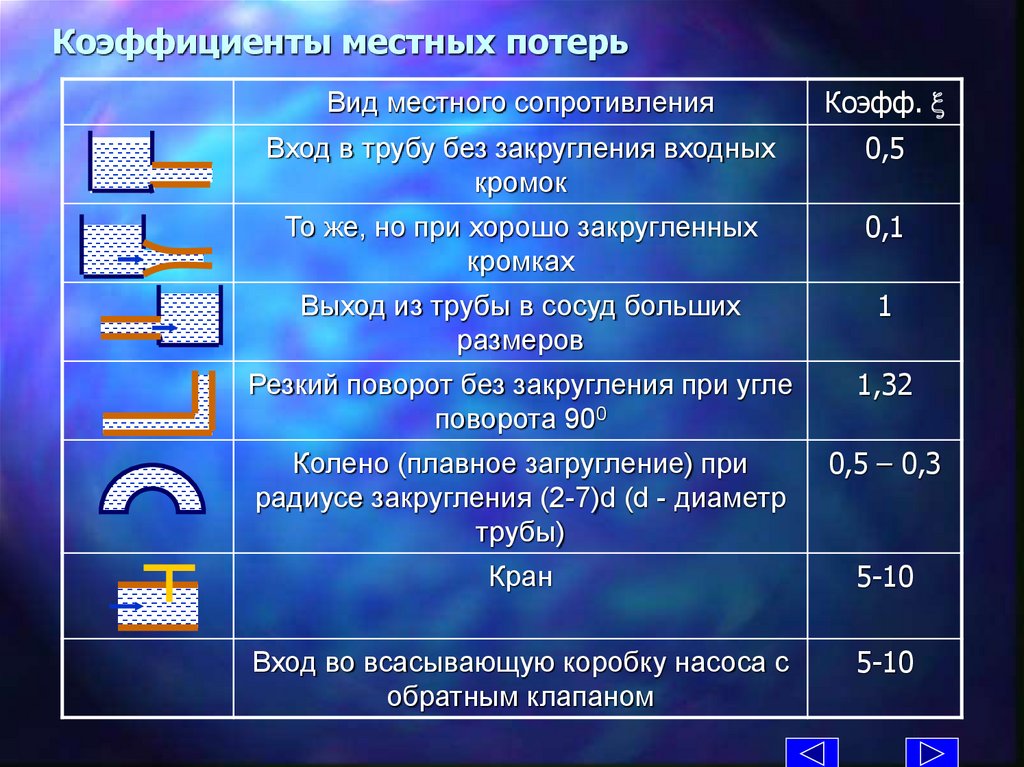
Коэффициенты местных потерьВид местного сопротивления
Коэфф.
Вход в трубу без закругления входных
кромок
0,5
То же, но при хорошо закругленных
кромках
0,1
Выход из трубы в сосуд больших
размеров
1
Резкий поворот без закругления при угле
поворота 900
1,32
Колено (плавное загругление) при
радиусе закругления (2-7)d (d - диаметр
трубы)
0,5 – 0,3
Кран
5-10
Вход во всасывающую коробку насоса с
обратным клапаном
5-10
22.
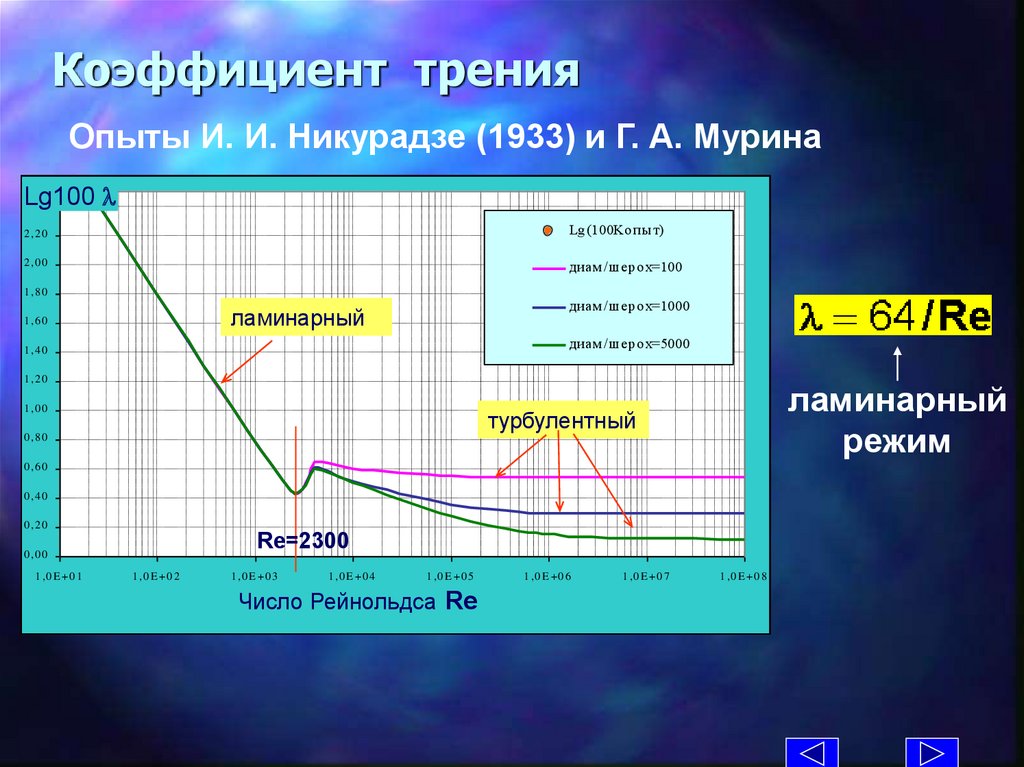
Коэффициент тренияОпыты И. И. Никурадзе (1933) и Г. А. Мурина
Lg100
2 ,4 0
2 ,2 0
Lg (100Kо пы т)
2 ,0 0
диам /ш ер о х=100
1 ,8 0
диам /ш ер о х=1000
ламинарный
1 ,6 0
диам /ш ер о х=5000
1 ,4 0
1 ,2 0
1 ,0 0
ламинарный
режим
турбулентный
0 ,8 0
0 ,6 0
0 ,4 0
0 ,2 0
Re=2300
0 ,0 0
1 ,0 E + 0 1
1 ,0 E + 0 2
1 ,0 E + 0 3
1 ,0 E + 0 4
1 ,0 E + 0 5
Ч и с ло Р е й н о льдсRe
а
Число Рейнольдса
1 ,0 E + 0 6
1 ,0 E + 0 7
1 ,0 E + 0 8
23.
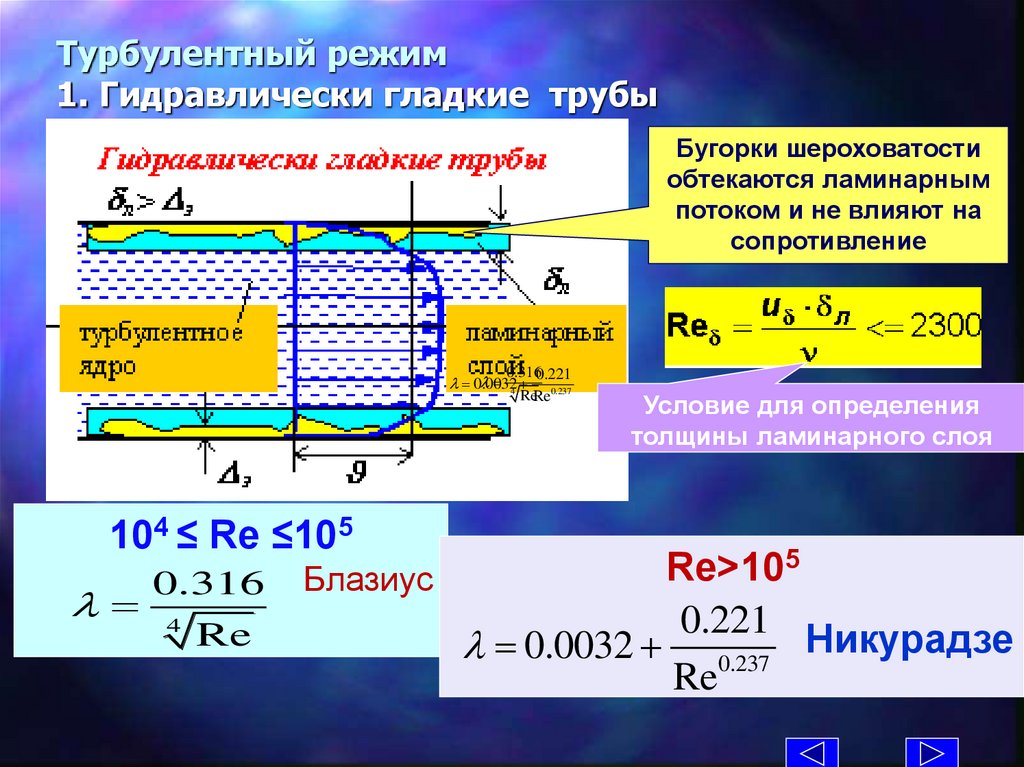
Турбулентный режим1. Гидравлически гладкие трубы
Бугорки шероховатости
обтекаются ламинарным
потоком и не влияют на
сопротивление
0.3160.221
ReRe0.237
= 4+
= 0.0032
104 ≤ Re ≤105
Условие для определения
толщины ламинарного слоя
5
Re>10
0.316 Блазиус
= 4
0.221
Re
= 0.0032 + 0.237 Никурадзе
Re
24.
Гидравлически шероховатые трубыПри увеличении скорости толщина ламинарного слоя уменьшается
Бугорки шероховатости
выступают в турбулентное ядро,
с них срываются вихри. А это
дополнительное сопротивление
При Re ≤ Rпред = 568 d / Δэ
Альтшуль
При дальнейшем увеличении скорости ламинарный слой очень тонкий.
Все бугорки шероховатости выступают в турбулентное ядро и
полностью определяют сопротивление трубы.
Re>Reпред
ý
= 0.11 Шифринсон
d
0.25
25.
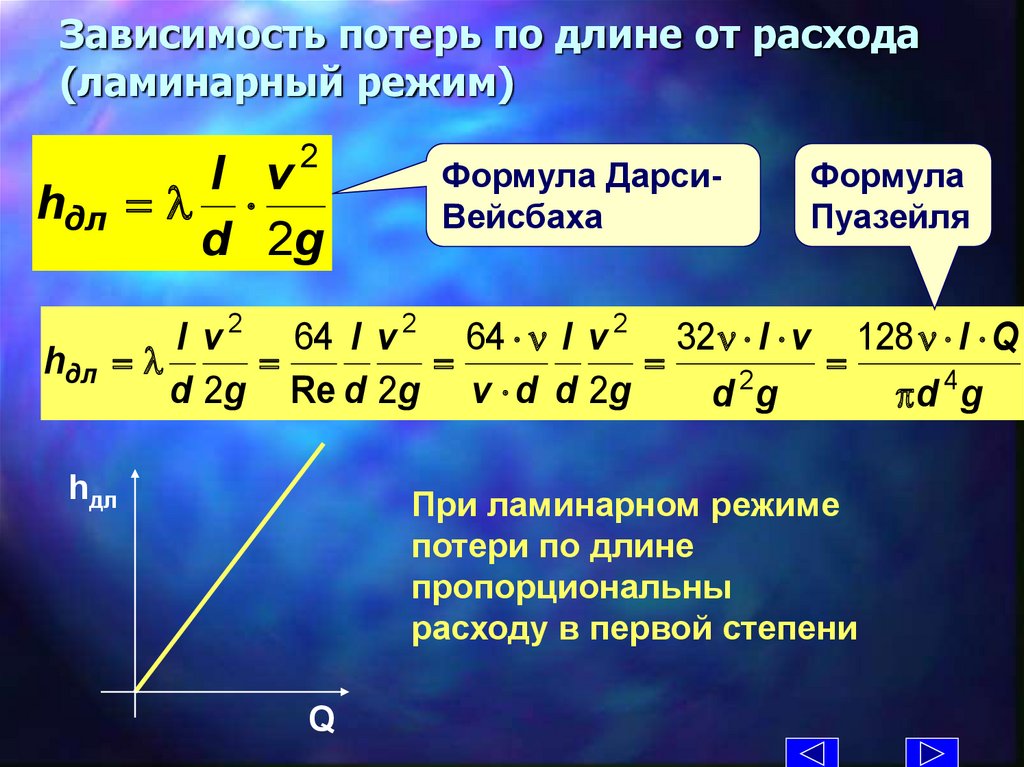
Зависимость потерь по длине от расхода(ламинарный режим)
2
l v
=
d 2g
hдл
hдл
Формула ДарсиВейсбаха
Формула
Пуазейля
l v 2 64 l v 2 64 l v 2 32 l v 128 l Q
=
=
=
=
=
2
d 2g Re d 2g v d d 2g
d g
pd 4 g
hдл
При ламинарном режиме
потери по длине
пропорциональны
расходу в первой степени
Q
26.
Зависимость потерь по длине от расхода(турбулентный режим)
hдл
l v2
=
d 2g
Формула ДарсиВейсбаха
68 э 0,2
= 0,11 (
+
)
v d d
hдл
lv
68 0,25 l v
=
= 0,11 (
)
v 1.75 Q1.75
d 2g
v d
d 2g
hдл
э 0,25 l v 2
l v2
=
= 0,11 ( )
v 2 Q2
d 2g
d
d 2g
2
2
Гидравлически
гладкие трубы
Абсолютно
шероховатые
трубы
hдл
При турбулентном режиме
потери по длине
пропорциональны Q 1.75-2
Q0
Q











 Физика
Физика








