Похожие презентации:
Закони розподілу. Лекція 7
1. ЗАКОНИ РОЗПОДІЛУ
План1. Характерні риси варіювання
2. Випадкові події
3. Ймовірність події і її властивості
4. Критерії достовірності оцінок. Статистичні
гіпотези
2. ХАРАКТЕРНІ РИСИ ВАРІЮВАННЯ
• В природі простежується широко поширеназакономірність:
• у масі щодо однорідних одиниць, що
становлять статистичну сукупність, більшість
середнього виявляється середнього або
близького до неї розміру, і чим далі вони
відстоять від середнього рівня варіюючої
ознаки, тим рідше зустрічаються в даній
сукупності.
• Це відбувається незалежно від форми
розподілу, що вказує на певний зв'язок між
числовими значеннями варіюючих ознак і
частотою їх трапляємості в даній сукупності.
• Наочним виразом цього зв'язку і є варіаційний
ряд і його лінійний графік — варіаційна крива.
• Цю закономірність можна відтворити апріорі у
вигляді математичної моделі, не побоюючись
впасти в суперечність з фактами.
3. ВИПАДКОВІ ПОДІЇ
• Будь який результат, випробування називаєтьсяподією.
• Під випробуванням, яке може повторюватись
нескінченну кількість раз, розуміють комплекс
умов, необхідних для того, щоб міг здійснитись
певний результат.
• У кожній із подій є лише один результат,
наперед передбачений. Такі події називаються
достовірними.
• Якщо ж при здійсненні комплексу умов події
відбутися не можуть, то вони називаються
неможливими.
4. ВИПАДКОВІ ПОДІЇ
• Події, результат яких при здійсненні комплексу умовточно передбачити не можна, називають
випадковими.
• Випадкові події (позначаються початковими
прописними буквами латинського алфавіту А, В, С,...)
називаються сумісними або несумісними, якщо в серії
випробувань всякий раз можливе здійснення лише
одного з них.
• Наприклад, при киданні монети вона може впасти
вгору гербом або peшкою. Тут два рівноможливих і
несумісних результатів. Події, які в даних умовах
можуть відбутися одночасно, називаються сумісними.
5. ЙМОВІРНІСТЬ ПОДІЇ ТА ЇЇ ВЛАСТИВОСТІ
• Згідно класичному визначенню,ймовірність події А виражається
відношенням кількості сприяючих
здійсненню цієї події результатів m до
кількості рівноможливих і несумісних
результатів n, тобто Р(А)=т/n.
6.
• Таким чином ймовірність являє собою число,розміщене між нулем і одиницею, і виражається
у відсотках від загального числа випробувань.
Таким чином, ймовірність достовірної події А
дорівнюватиме одиниці, а ймовірність
неможливої події А дорівнюватиме нулю.
• З цих аксіоматичних властивостей ймовірності
виходить, що ймовірність події А і ймовірність
протилежної події Р (Ане) в сумі дорівнює
одиниці, тобто Р(А)+Р (Ане) = 1.
7.
• Вважають, що події, які мають дуже малу ймовірність,в одиничних випробуваннях не відбудуться, тобто
такі події розглядають як практично неможливі. Якщо
ж ймовірність події достатньо висока, то її прийнято
вважати практично достовірною.
• Для спрощення символіки прийняте значення
ймовірність очікуваної події позначати латинською
буквою р, тобто тим же знаком, яким позначається
частка, а значення ймовірність протилежної події —
буквою q, тобто Р(А)=р і P(Aне)=q, звідки p+q=1.
• Ймовірність, яку можна вказати до проведення
експерименту, називають апріорною.
• Коли ймовірність здійснення подій може бути
встановлена лише на підставі експерименту, то
ймовірність називається апостеріорною.
8.
• на відміну від «класичної» ймовірностічастки випадкових подій, а точніше — їх
крайні значення, що володіють певною
стійкістю, прийнято називати
статистичною ймовірністю цих подій.
9. КРИТЕРІЇ ДОСТОВІРНОСТІ ОЦІНОК. СТАТИСТИЧНІ ГІПОТЕЗИ
В біометрії широке застосування отримала нульова гіпотеза (Н0). Її сутьзводиться до припущення, що різниця між генеральними параметрами
порівнюваних груп дорівнює нулю і що відмінності, які спостерігаються
між вибірковими характеристиками, мають не системний, а виключно
випадковий характер. Так, якщо одна вибірка взята з сукупності, що
нормально розподіляється, з параметрами х та х , а інша — з
сукупності з параметрами у та у , то нульова гіпотеза виходить з того,
що:
х у та х у , тобто х у 0 та
х у 0 (звідси і назва гіпотези — нульова).
Протилежна нульовій — альтернативна гіпотеза (На) – виходить з
припущення, що
х у 0
та
х у 0
10.
Для перевірки прийнятої гіпотези, а отже, й достовірності оцінкигенеральних параметрів за вибірковими даними використовують
величини, функції розподілу яких відомі. Ці величини, називаються
критеріями ймовірності, дозволяють у кожному конкретному випадку
виявити, чи задовольняють вибіркові показники прийняту гіпотезу.
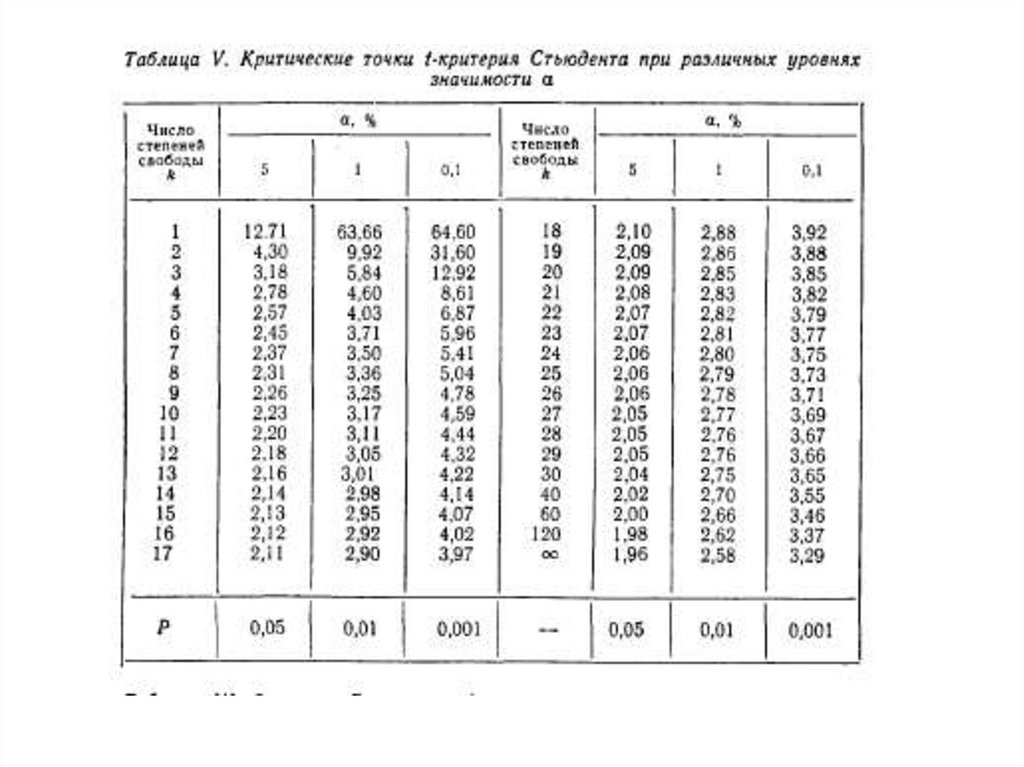
Функції розподілу вказаних величин зведені в спеціальні таблиці, де
містяться значення функції для різних чисел ступенів свободи k або
об'єму вибірки n і рівнів значущості а.
Рівень значущості, або ймовірність похибки, що допускається при
оцінці прийнятої гіпотези, може розрізнятися. Зазвичай, при перевірці
статистичних гіпотез приймають три рівні значущості: 5%-вий
(ймовірність похибки Р = 0,05), 1%-вий (Р = 0,01) і 0,1%-вий (Р = 0,001).
У біологічних дослідженнях часто вважають достатнім 5%-вий рівень
значущості. При цьому нульову гіпотезу не відкидають, якщо в результаті
дослідження виявиться, що ймовірність похибки оцінки щодо
правильності прийнятої гіпотези перевищує 5%, тобто Р>0,05. Якщо ж
Р<0,05, то прийняту гіпотезу слід відкинути на взятому рівні (а). Помилка
при цьому можлива не більше ніж в 5% випадків, тобто вона
малоймовірна.
11.
12.
При відповідальніших дослідженнях рівень значущості може бутизменшений до 1 або навіть до 0,1%. Трьом згаданим рівням
значущості (а) відповідають (при нормальності розподілу
використовуваного критерію) нормовані відхилення (t): при а1(Р =
0,05) нормоване відхилення t1 = l,96; при а2 (Р = 0,01) — t2 = 2,58;
при а3 (Р = 0,001) — t3 = 3,29; і відповідно пороги довірчої
ймовірності (1 – а) дорівнюють P1 = 0,95, P2 = 0,99 і Р3 = 0,999.
В біометрії застосовують два види статистичних критеріїв:
- параметричні, побудовані на основі параметрів певної сукупності
(наприклад, х і s2x), які являють собою функції цих параметрів;
- непараметричні, є функціями, залежними безпосередньо від
варіант даної сукупності з їх частотами.
З параметричних критеріїв в біометрії застосовують t-критерій
Стьюдента та F-критерий Фішера. Перший використовують для
порівняльної оцінки середніх величин, другий — для оцінки
дисперсій.











 Математика
Математика








