Похожие презентации:
Функція розподілу випадкової величини та її головні характеристики. Нормальний розподіл
1. Функція розподілу випадкової величини та її головні характеристики. Нормальний розподіл
1.2.
3.
4.
5.
6.
Дискретні та неперервні випадкові величини.
Закон розподілу ймовірностей дискретної випадкової
величини: (приклади: біноміальний розподіл, розподіл
Пуассона)
Математичне сподівання, дисперсія і середньоквадратичне
відхилення дискретної випадкової величини, їх властивості.
Властивості розподілів неперервної випадкової величини.
Нормальний розподіл. Вплив параметрів нормального
розподілу на форму нормальної кривої.
Обчислення ймовірності заданого відхилення. Правило трьох
сигм.
2. 1. Дискретні та неперервні випадкові величини
випадкова величина (ВВ) – величина, яка врезультаті випробування прийме одне і тільки
одне можливе значення, що наперед невідоме і
залежить від випадкових причин, які завчасно
(перед випробуванням) не можуть бути
враховані
дискретна ВВ – ВВ,
яка приймає окремі,
ізольовані можливі
значення з певними
ймовірностями
Кількість можливих
значень – скінчена або
нескінченна
Неперервна ВВ – ВВ,
яка приймає всі
можливі значення з
певного скінченого або
нескінченного проміжку
Кількість можливих
значень - нескінченна
3. 2. Закон розподілу ймовірностей ДВВ
Закон розподілу ДВВ– відповідність між
можливими
значеннями ВВ і їх
ймовірностями.
Х
х1 х 2 x3 x4 х5
Р
р1 р2 p3 p4 p5
Задається: графічно,
n
аналітично,
pi 1
таблично:
p2
p5p
4
p1
i 1
Хi
х1 х2 ... хn
Рi
р1 р2 ... pn
p f (x)
Pі
p3
x1x2
x3 x4
x5 Xі
4. Приклад:
Умова:У клітці 20 щурів: 1 –
білий, 10 – сірих і 9
чорних. Навмання
витягли 1 щура.
Знайти закон
розподілу для
випадкової величини Х
– кольору щура
Х
1
2
Р
1/20
1/2
Розв’язок:
Можливий колір
позначимо 1 – білий, 2
– сірий, 3 – чорний,
тобто:
х1 =1,
х2 = 2,
х3 = 3.
Для цих значень
ймовірності є:
р1 = 1/20,
р2 = ½,
3
р3 = 9/20
9/20
5. Біноміальний розподіл
Нехай проводятьn незалежних
випробувань;
ймовірність появи
події А у кожному з
них р (не появи –
q=1-p).
Ймовірність появи
події А рівно k разів
у n випробуваннях:
Pn (k ) C p q
k
n
k
n k
Формула Бернуллі
Біноміальний
розподіл – це
розподіл
ймовірностей, який
визначається
формулою Бернуллі:
x
n
n-1
…
p
pn n*pn-1*q … Cnk*pk*qn-k … qn
n!
C
k!(n k )!
k
n
k
… 0
6. Найімовірніше число появи події А у випадку біноміального розподілу:
np q k0 np q7. Приклад:
Х0
1
2
3
Р
0,118
0,367
0,382
0,133
Розв’язок:
Умова:
q=1-0.51=0.49
У сім’ї народилась
Можливо, що в трійні буде
трійня. Знайти закон
0, 1, 2 і 3 хлопчиків,
розподілу кількості
хлопчиків, коли
тоді ймовірності цих
ймовірність
подій:
народження
P3 (0) C30 0.510 0.493 0.493 0,117649,
хлопчика = 0,51 P (1) C 1 0.511 0.493 1 3 0.51 0.49 2 0,367353,
3
3
P3 (2) C32 0.512 0.493 2 3 0.512 0.49 0,382347,
P3 (3) C33 0.513 0.490 0.513 0,132651,
перевірка :
0,117649 0,367353 0,382347 0,132651 1
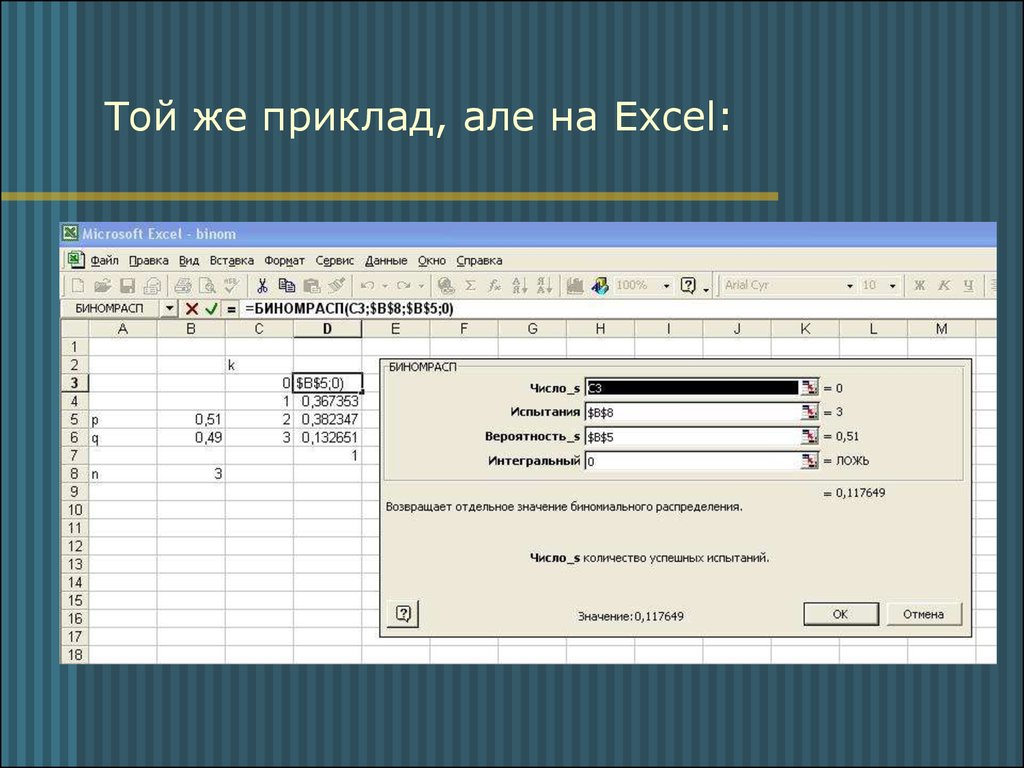
8. Функція БИНОМРАСП:
9. Той же приклад, але на Excel:
10. Розподіл Пуассона
Він є - випадок збіноміального розподілу
(коли р – дуже мале
значення, а n – велике),
ймовірність появи рівно k
разів події А у n
випробуваннях:
ak
Pn (k )
, де a np
a
k! e
а – найімовірніше число
появи події А
11. Приклад:
Умова:Підручник зі статистики
видано тиражем 5 000
примірників. Ймовірність
неправильного
брошурування = 0,0006.
а) Яка ймовірність, що 4
книги буде неправильно
зброшуровано?
б) Яка найімовірніша
кількість книг буде
бракованою? Яка її
ймовірність?
Розв’язок:
Маємо: n=5000,
p=0.0006, k=4, тоді:
а)
(0.0006 * 5000) 4
P5000 (4)
0,168
3
4!e
a 0.0006 * 5000 3
б)
a 0.0006 * 5000 3
(3) 3
P5000 (3)
0,224
3
3!e
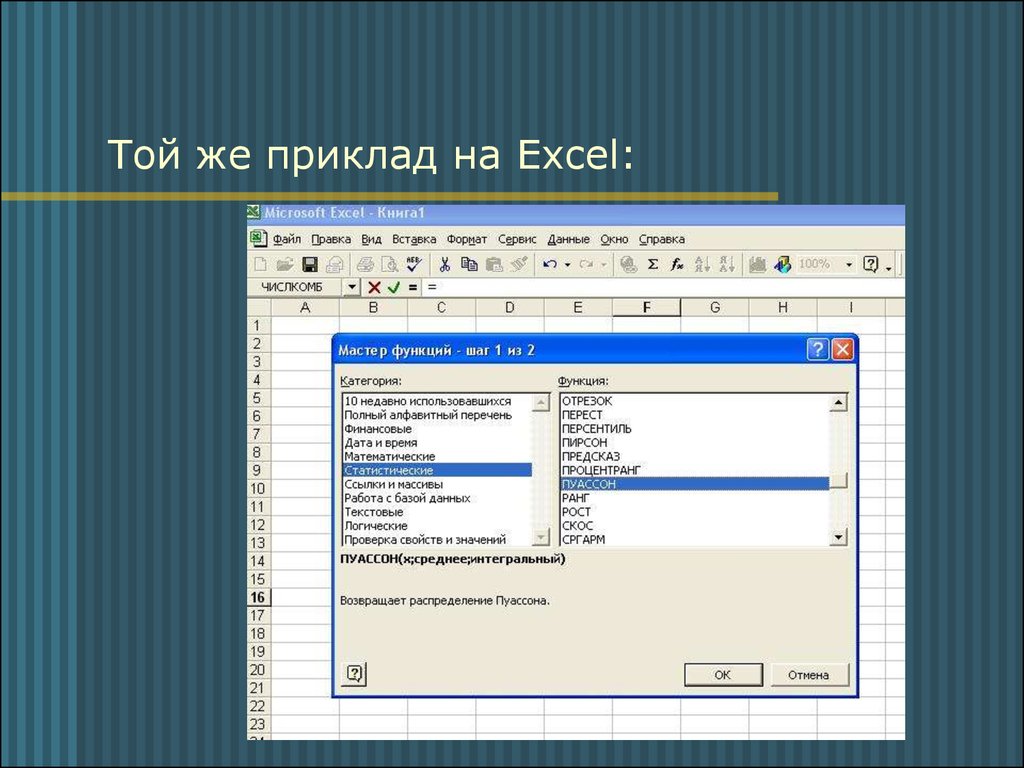
12. Той же приклад на Excel:
13.
14.
15. 3. Числові характеристики ДВВ і їх властивості
Математичнесподівання – це
характеристика
середнього значення
ВВ;
- це сума добутків
всіх можливих
значень ДВВ на їх
ймовірності:
M ( X ) x1 p1 x2 p2 ... xn pn
n
M ( X ) xi pi
i 1
Властивості:
Математичне сподівання
константи дорівнює самій
константі:
М(С)=С
Постійний множник можна
виносити за знак математичного
сподівання:
М(СХ)=С*М(Х)
Мат.сподівання добутку взаємно
незалежних ВВ дорівнює добутку
їх мат.сп.:
М(Х1Х2...Хn)=М(Х1)*М(Х2)*...*М(Хn)
Для суми взаємно незалежних
ВВ:
М(Х1 + Х2 +...+ Хn) = М(Х1)+М(Х2)
+...+ М(Хn)
Для біноміального закону
М(Х)=n*p=а
16. Дисперсія:
- характеристикарозсіяння можливих
значень ВВ навколо
М(Х)
- це математичне
сподівання квадрату
відхилень ВВ від її
математичного
сподівання:
D( X ) M [ X M ( X )]2
D( X ) M ( X 2 ) [ M ( X )]2
Властивості:
Дисперсія константи дорівнює 0:
D(C)=0,
Постійний множник можна
виносити за знак дисперсії,
попередньо встановивши його
квадрат:
D(CX)=C2*D(X),
Дисперсія суми незалежних
величин:
D(X1+X2+…+Xn) =
D(X1)+D(X2)+…+D(Xn)
Дисперсія добутку незалежних
величин:
D(X1*X2*…*Xn) =
D(X1)*D(X2)*…*D(Xn)
Для біноміального розподілу:
D(X)=n*p*q
17. Середнє квадратичне відхилення:
- характеристикарозсіяння можливих
значень ВВ навколо
М(Х)
- це квадратний
корінь з дисперсії
( X ) D( X )
18. Приклад:
Х0
Р
1
2
3
0,118 0,367 0,382 0,133
Приклад:
Знайти
математичне
сподівання,
дисперсію і
середнє
квадратичне
відхилення для
даних ймовірності
появи хлопчиків у
трійні:
Математичне сподівання:
M ( X ) 0 * 0.118 1* 0.367
2 * 0.382 3 * 0.133 1.53
Дисперсія:
Р
0,118 0,367 0,382 0,133
Х2
0
1
4
9
Р*Х2
0
0,367
3,059
3,582
D( X ) M ( X 2 ) [ M ( X )]2
7.01 1.532 7.01 2.34 4.67
Середньоквадратичне
відхилення: ( X ) D( X ) 2.16
19. 3. Неперервні ВВ. Нормальний розподіл.
Випадковавеличина Х є
нормально
розподіленою,
коли її функція
густини (значення
ймовірності рі
будь-якого хі
знаходиться в
інтервалі (х1 + ( x a )
2
f
(
x
)
e
dx)) має вигляд:
2
i
2
а – математичне
сподівання,
σсередньоквадратич
не відхилення
ПРИ: а = 0, σ = 1,
функція
називається
1 ( x2)
Функцією
F ( x) Лапласа:
e
2
2
i
2
20. Нормальний розподіл (продовження):
Ймовірністьвлучення в будьякий інтервал
(a; b) нормально
розподіленої
випадкової
величини
розраховується:
P ( a x b) F (
b m
) F(
a m
)
21. Нормальний розподіл (продовження):
Ймовірність того, що абсолютна величинавідхилення менше додатного числа у
y
P( x a y ) 2 F ( )
Правило 2 та 3 σ(2 і 3 сигм) : 95,45% і 99,73%
всіх незалежних спостережень з нормальної
сукупності лежить, відповідно, в зоні 2 і 3
стандартних відхилень від середнього
значення.
22. Приклад:
Математичнесподівання нормально
розподіленої
випадкової величини
Х дорівнює 3,
середньоквадратичне
відхилення = 2.
Написати густину
ймовірності Х.
Використаємо
формулу:
1
f ( x)
e
2
1
e
2 2
( xi 3 ) 2
2 2 2
( xi a ) 2
2 2
1
e
2 2
( xi 3 ) 2
8
23. Приклад:
Математичне сподівання ісередньоквадратичне
відхилення нормально
розподіленої випадкової
величини Х, відповідно,
дорівнюють 10 і 2.
Знайти ймовірність того,
що в результаті
випробування Х прийме
значення, яке буде
міститись в інтервалі (12,
14).
Маємо формулу:
P ( a x b) F (
b m
) F(
a m
)
14 10
12 10
P(12 x 14) F (
) F(
)
2
2
F (2) F (1) 0.4772 0.3413 0.1359
24. Приклад:
Зважують речовину безМаємо:
систематичних похибок.
y
Випадкові похибки
P( x a y ) 2 F ( )
зважування
підкорюються
нормальному закону з P( x 10) 2F (10 ) 2F (0.5) 2 0.1915 0.383
20
середньоквадратичним
відхиленням 20 мг.
Знайти ймовірність того,
що зважування буде
здійснене з похибкою,
яка не перевищить за
абсолютною величиною
10 мг.






















 Математика
Математика








