Похожие презентации:
Статически определимые плоские фермы
1. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ ПЛОСКИЕ ФЕРМЫ
2.
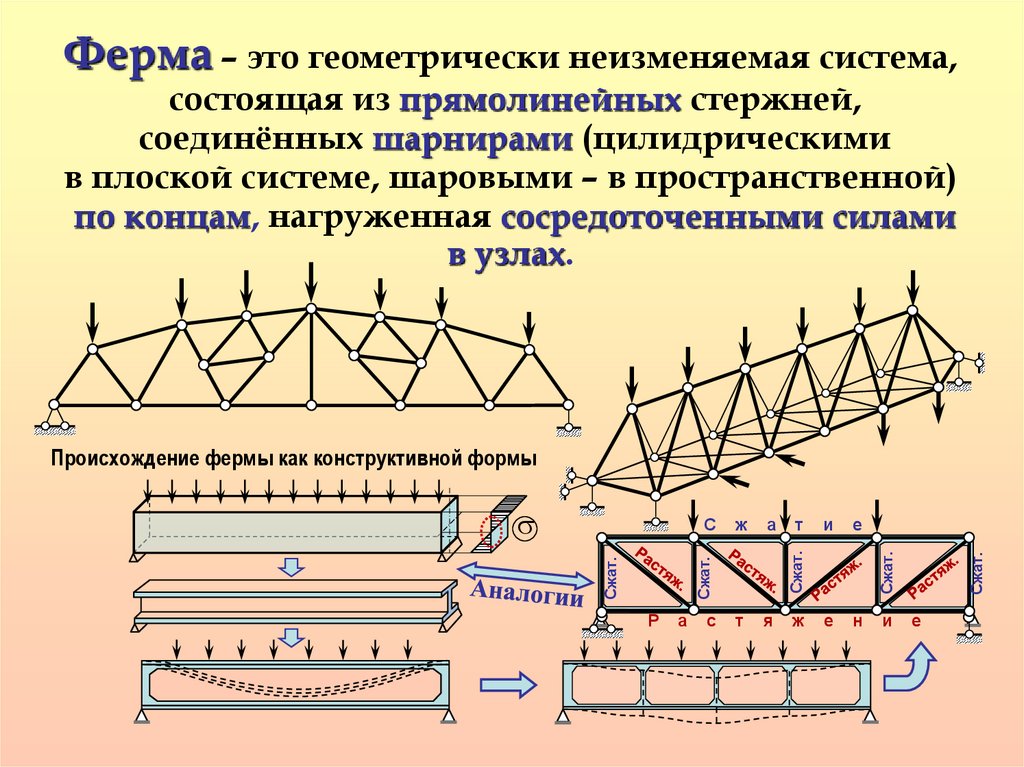
Ферма – это геометрически неизменяемая система,состоящая из прямолинейных стержней,
соединённых шарнирами (цилидрическими
в плоской системе, шаровыми – в пространственной)
по концам, нагруженная сосредоточенными силами
в узлах.
Происхождение фермы как конструктивной формы
а
а
с
т
я
и
е
ж
е
н
Сжат.
Сжат.
Р
т
и
Сжат.
ж
Сжат.
С
Сжат.
s
е
3.
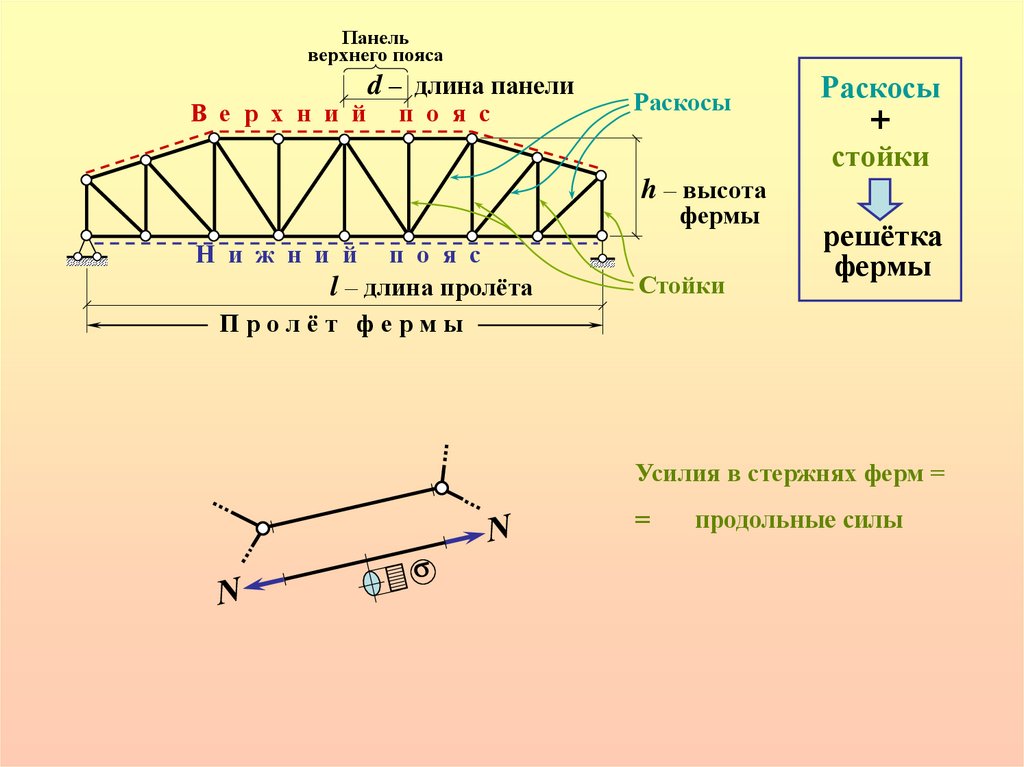
Панельверхнего пояса
В е р х н и й
d – длина панели
п о я с
Раскосы
Раскосы
+
стойки
h – высота
фермы
Н и ж н и й п о я с
l – длина пролёта
Пролёт фермы
Стойки
решётка
фермы
Усилия в стержнях ферм =
=
продольные силы
4.
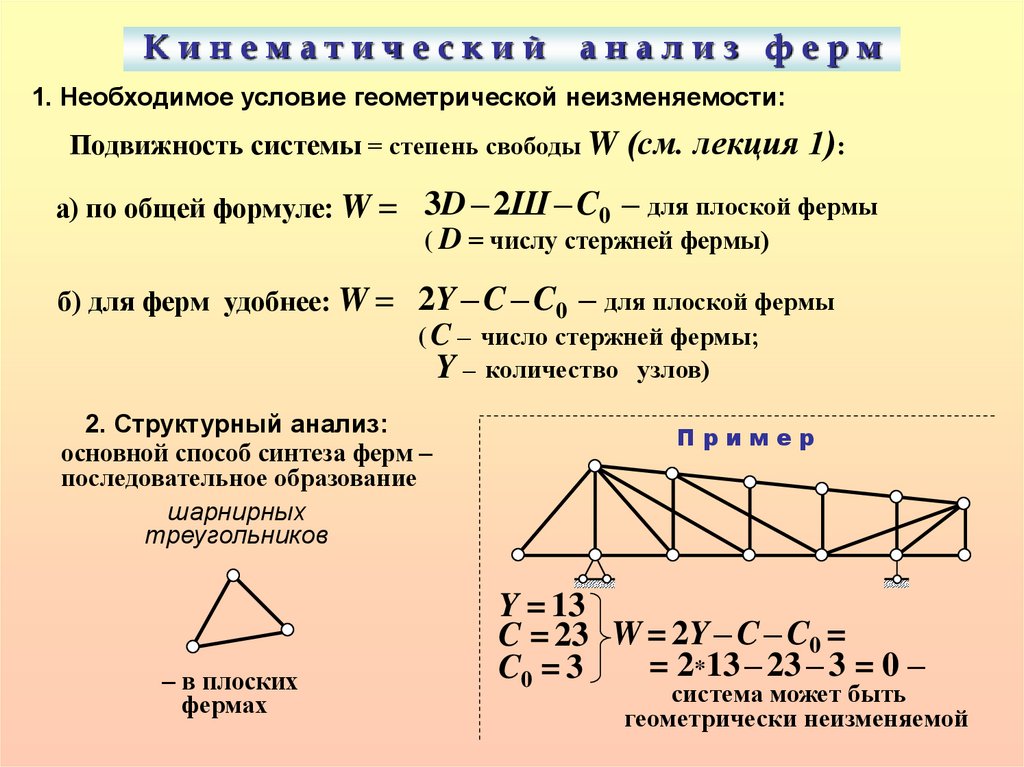
Кинематическийанализ ферм
1. Необходимое условие геометрической неизменяемости:
Подвижность системы = степень свободы W (см. лекция 1):
а) по общей формуле: W = 3D – 2Ш – C0 – для плоской фермы
( D = числу стержней фермы)
б) для ферм удобнее: W = 2Y – C – C0 – для плоской фермы
( C – число стержней фермы;
Y – количество узлов)
2. Структурный анализ:
основной способ синтеза ферм –
последовательное образование
шарнирных
треугольников
– в плоских
фермах
Пример
Y = 13
C = 23 W = 2Y – C – C0 =
= 2*13 – 23 – 3 = 0 –
C0 = 3
система может быть
геометрически неизменяемой
5.
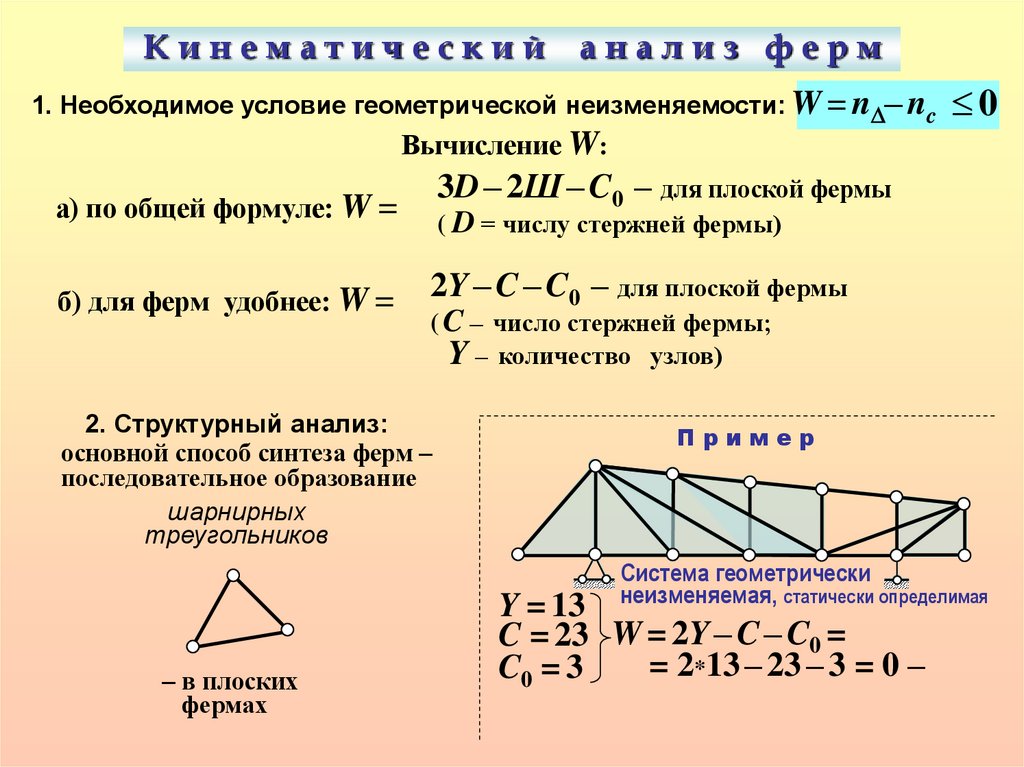
Кинематическийанализ ферм
1. Необходимое условие геометрической неизменяемости: W = nD– nc 0
Вычисление W:
а) по общей формуле: W =
3D – 2Ш – C0 – для плоской фермы
б) для ферм удобнее: W =
2Y – C – C0 – для плоской фермы
( D = числу стержней фермы)
( C – число стержней фермы;
Y – количество узлов)
2. Структурный анализ:
основной способ синтеза ферм –
последовательное образование
шарнирных
треугольников
Пример
Система геометрически
неизменяемая, статически определимая
– в плоских
фермах
Y = 13
C = 23 W = 2Y – C – C0 =
= 2*13 – 23 – 3 = 0 –
C0 = 3
6.
Определение продольных сил в стержнях фермСтатические методы определения усилий
(продольных сил) в стержнях ферм
F
N2 = F
2а) незагруженный:
1. Двухстержневой узел
N2 = 0
ΣПр2-2 = 0
2. Трёхстержневой узел частного вида (Т – образный)
Частные случаи
равновесия узлов фермы
1б) загруженный
по направлению
одного из
стержней:
F
ΣПр1-1 = 0
Для узла можно составить
2 уравнения равновесия,
например
N1
2
N1 = 0
- моментной точки
(Риттера)
- проекций
2
N3 = N1
1а) незагруженный:
- вырезания
узлов узлов
Способ
вырезания
2б) загруженный по
направлению одиночного
стержня:
N1
N3 = N1
F
N2 = 0
N3 = N1
N1
N2 = F
N1 = F
N2 = 0
3. Четырёхстержневой
Х – образный узел
N2
N3
N1 = N3
N4 = N2
7.
Определение продольных сил в стержнях фермСтатические методы определения усилий
(продольных сил) в стержнях ферм
- вырезания узлов
моментной
точки
- Способ
моментной
точки
(Риттера)
(Риттера)
- проекций
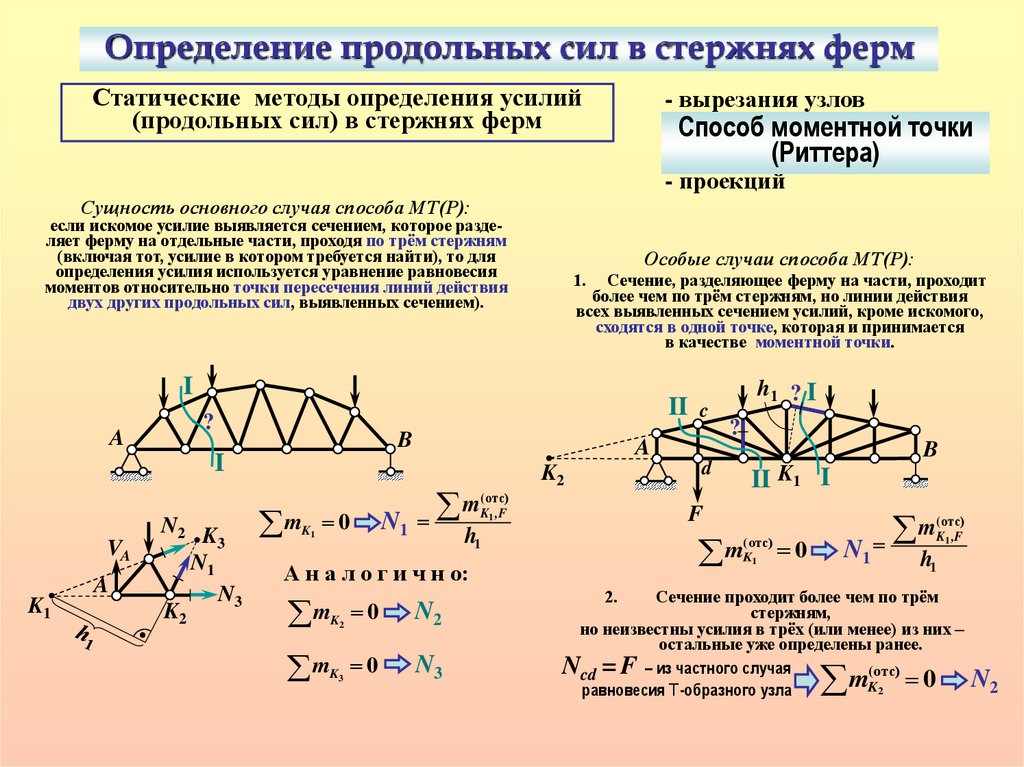
Сущность основного случая способа МТ(Р):
если искомое усилие выявляется сечением, которое разделяет ферму на отдельные части, проходя по трём стержням
(включая тот, усилие в котором требуется найти), то для
определения усилия используется уравнение равновесия
моментов относительно точки пересечения линий действия
двух других продольных сил, выявленных сечением).
Особые случаи способа МТ(Р):
1.
Сечение, разделяющее ферму на части, проходит
более чем по трём стержням, но линии действия
всех выявленных сечением усилий, кроме искомого,
сходятся в одной точке, которая и принимается
в качестве моментной точки.
I
A
II c
?
B
A
I
VA
K1
A
N2 K
3
N1
N3
K2
m 0
K1
m
N
1
K2
( отс)
K1 ,F
m 0
N3
K3
B
II K1 I
F
m
(отс)
K1
А н а л о г и ч н о:
N2
?
d
h1
mK2 0
h1 ? I
0
m
N
1
2.
( отс)
K1 ,F
h1
Сечение проходит более чем по трём
стержням,
но неизвестны усилия в трёх (или менее) из них –
остальные уже определены ранее.
Ncd = F – из частного случая
(отс)
m
0 N2
K
2
равновесия Т-образного узла
8.
Определение продольных сил в стержнях фермСтатические методы определения усилий
(продольных сил) в стержнях ферм
- вырезания узлов
моментной
точки
- Способ
моментной
точки
(Риттера)
(Риттера)
- проекций
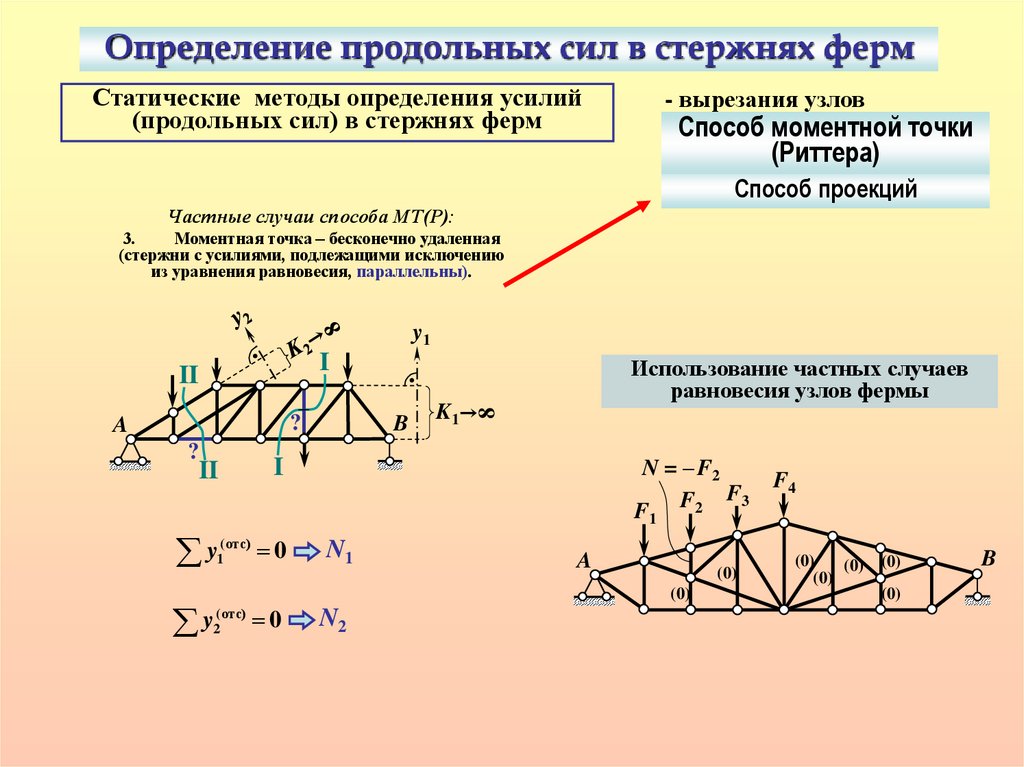
Способ проекций
Частные случаи способа МТ(Р):
3.
Моментная точка – бесконечно удаленная
(стержни с усилиями, подлежащими исключению
из уравнения равновесия, параллельны).
y1
I
?
A
?
II
Использование частных случаев
равновесия узлов фермы
B
K1
8
II
N = – F2
F3
F
2
F
I
F4
1
y
(отс)
1
y
(отс)
2
0
N1
A
(0)
(0)
0
N2
(0)
(0)
(0)
(0)
(0)
B
9.
ЛИНИИ ВЛИЯНИЯ УСИЛИЙВ СТЕРЖНЯХ ФЕРМ
10.
хF=1
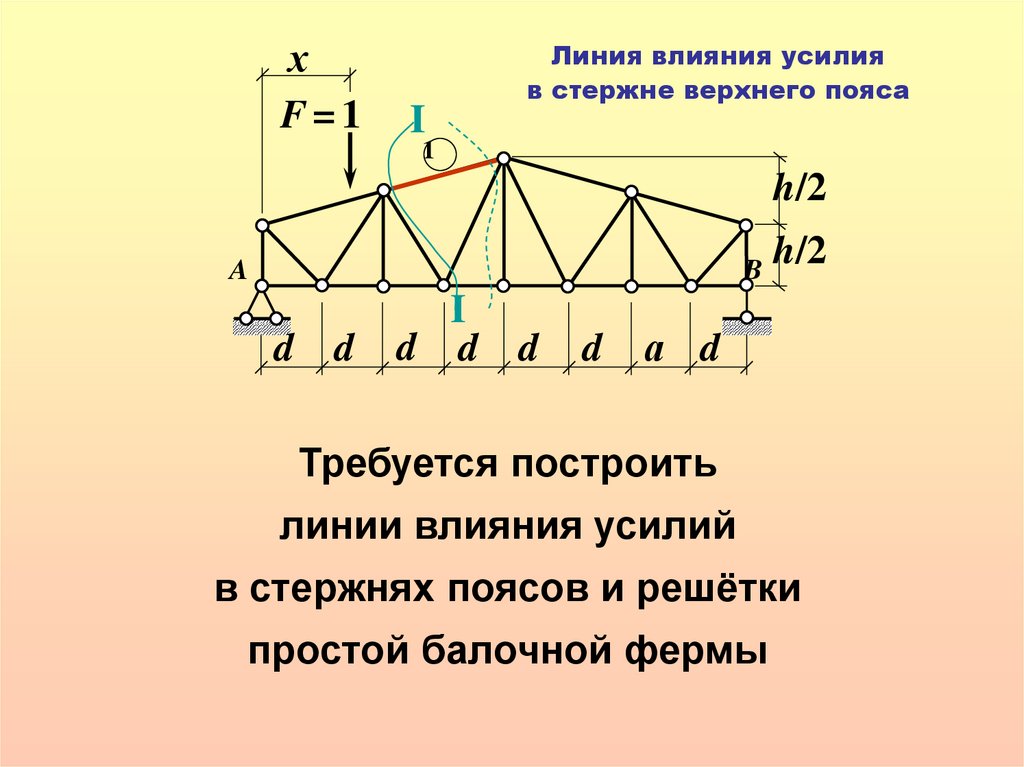
Линия влияния усилия
в стержне верхнего пояса
I
1
h/2
A
B
d
d
I
d d
d
d
h/2
а d
Требуется построить
линии влияния усилий
в стержнях поясов и решётки
простой балочной фермы
11.
хF=1
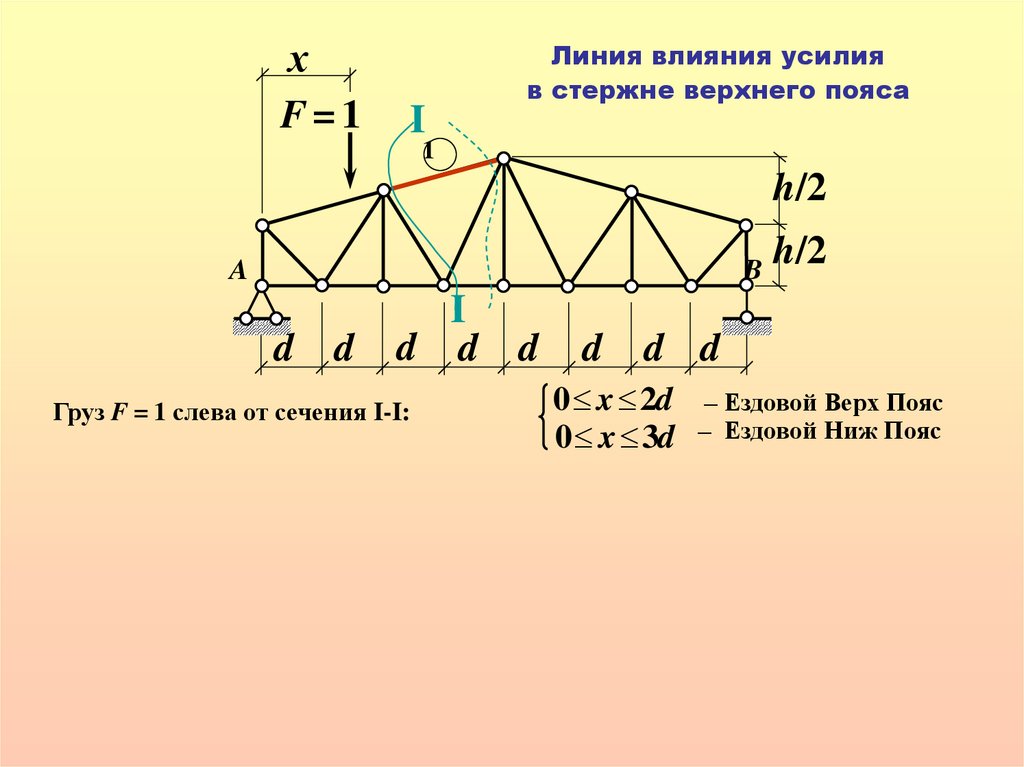
Линия влияния усилия
в стержне верхнего пояса
I
1
h/2
A
B
d
d
I
d d
Груз F = 1 слева от сечения I-I:
d
d
h/2
d d
0 x 2d – Ездовой Верх Пояс
0 x 3d – Ездовой Ниж Пояс
12.
хF=1
Линия влияния усилия
в стержне верхнего пояса
I
1
h/2
A
B
d
d
I
d d
d
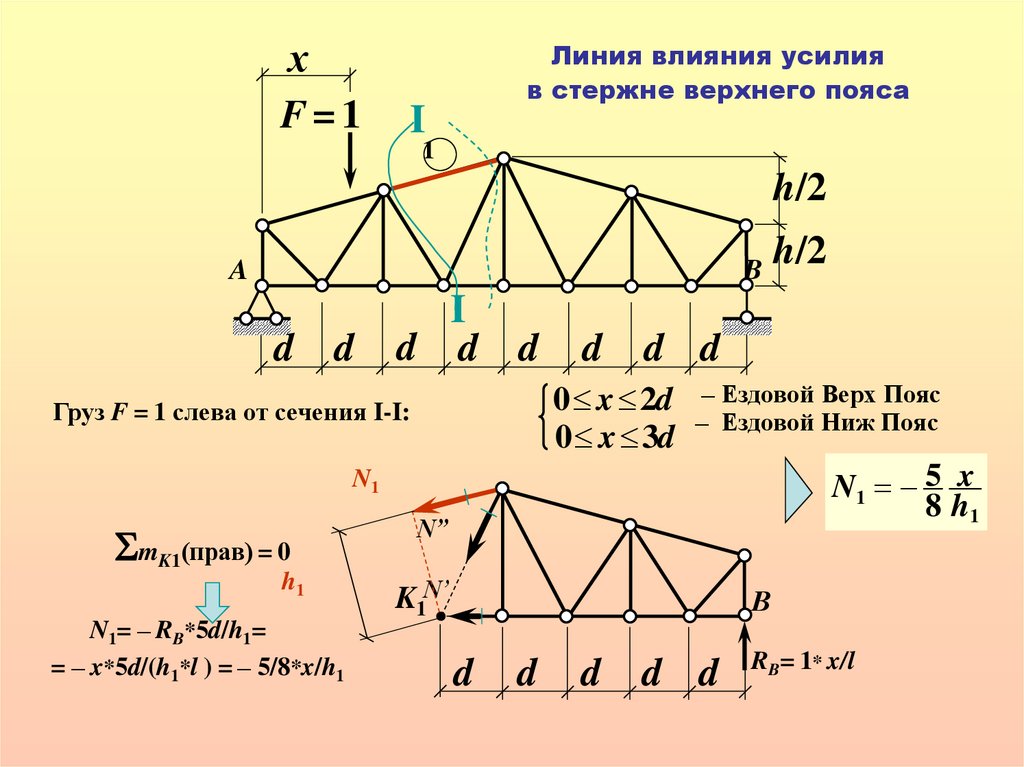
N1
SmK1(прав) = 0
h1
K1N’
N1= – RB*5d/h1=
= – x*5d/(h1*l ) = – 5/8*x/h1
d d
0 x 2d – Ездовой Верх Пояс
– Ездовой Ниж Пояс
0 x 3d
N1 5 x
8 h1
Груз F = 1 слева от сечения I-I:
N”
d
h/2
В
d
d
d
d d
RB= 1* x/l
13.
хF=1
Линия влияния усилия
в стержне верхнего пояса
I
1
h/2
A
B
d
d
I
d d
d
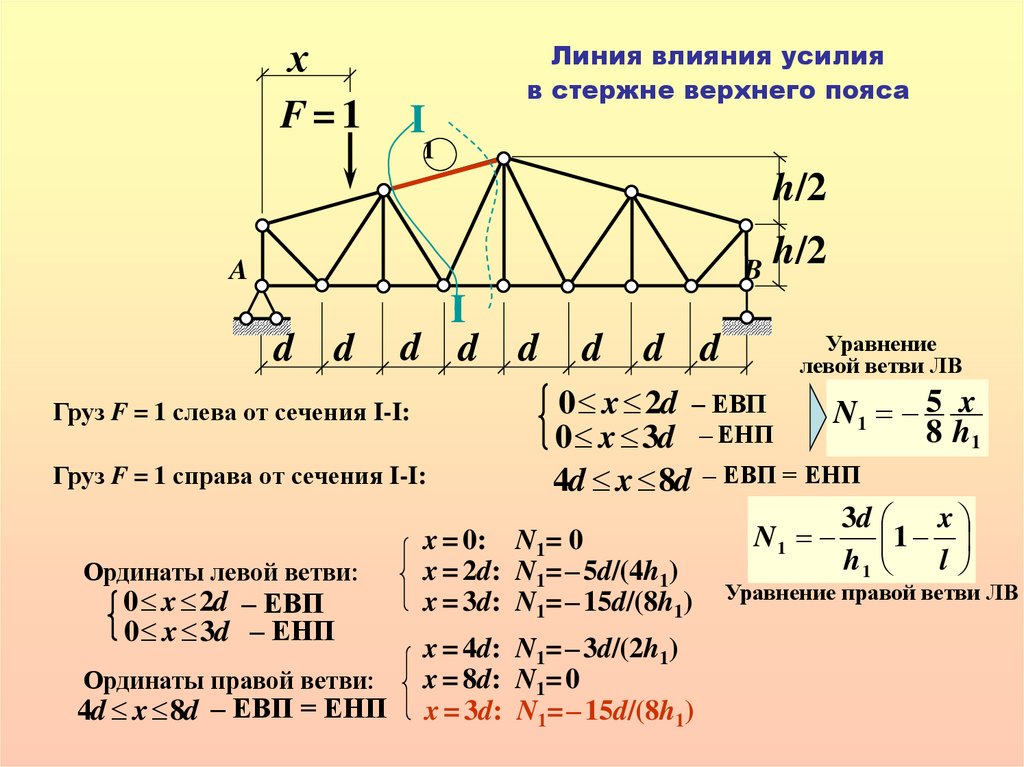
Груз F = 1 справа от сечения I-I:
N1
A
RА= 1* (1 – x/l )
3а
K1
Уравнение
левой ветви ЛВ
d d
0 x 2d – ЕВП
5 x
N
1
8 h1
0 x 3d – ЕНП
4d x 8d – ЕВП = ЕНП
Груз F = 1 слева от сечения I-I:
N”
d
h/2
h1
N’
3d
x
N
1
SmK1(лев) = 01 h 1 l
Уравнение правой ветви ЛВ
N1= – RA*3d/h1=
= – (1 – x/l )*3d/h1
14.
хF=1
Линия влияния усилия
в стержне верхнего пояса
I
1
h/2
A
B
d
d
I
d d
Груз F = 1 слева от сечения I-I:
Груз F = 1 справа от сечения I-I:
d
d
d d
Ординаты левой ветви:
Ординаты правой ветви:
x = 4d: N1= – 3d/(2h1)
x = 8d: N1= 0
x = 3d: N1= – 15d/(8h1)
4d x 8d – ЕВП = ЕНП
Уравнение
левой ветви ЛВ
0 x 2d – ЕВП
N1 5 x
8 h1
0 x 3d – ЕНП
4d x 8d – ЕВП = ЕНП
x = 0: N1= 0
x = 2d: N1= – 5d/(4h1)
x = 3d: N1= – 15d/(8h1)
0 x 2d – ЕВП
0 x 3d – ЕНП
h/2
N1
3d
x
1
h1
l
Уравнение правой ветви ЛВ
15.
хF=1
Линия влияния усилия
в стержне верхнего пояса
I
1
h/2
A
B
h/2
K1 I
Правило:
левая и правая
ветви (или их
продолжения)
пересекаются
под моментной
точкой К1
d
d
d
d
d
d
Л.В. N1
Ординаты левой ветви:
Ординаты правой ветви:
x = 4d: N1= – 3d/(2h1)
x = 8d: N1= 0
x = 3d: N1= – 15d/(8h1)
4d x 8d – ЕВП = ЕНП
N1 5 x
8 h1
Соединительные прямые
при ЕВП и ЕНП
x = 0: N1= 0
x = 2d: N1= – 5d/(4h1)
x = 3d: N1= – 15d/(8h1)
0 x 2d – ЕВП
0 x 3d – ЕНП
Уравнение
левой ветви ЛВ
d d
N1
3d
x
1
h1
l
Уравнение правой ветви ЛВ
16.
хF=1
Линия влияния усилия
в стержне нижнего пояса
II
h/2
B h/2
2
A
II
d
d
d
d
Груз F = 1 слева
от сечения II-II:
0 x 4d (ЕВП = ЕНП) h
Груз F = 1 справа
от сечения II-II:
6d x 8d – ЕВП
5d x 8d– ЕНП
N2
d
d
RА= 1* (1 – x/l )
SmK2(прав) = 0
K2 N**
N*
Уравнение
левой ветви ЛВ
B
K2
N**
h
N*
A
d d
N2
SmK2(лев) = 0
N2 x
2h
RB= 1* x/l
Уравнение правой ветви ЛВ
N2 4a 1 x
h
l
17.
хF=1
Линия влияния усилия
в стержне нижнего пояса
K2
II
h/2
B h/2
2
A
II
Правило:
левая и правая
ветви (или их
продолжения)
пересекаются
под моментной
точкой К2
d
d
d
d
d
d
d d
Соединительные прямые
при ЕНП и ЕВП
Ординаты левой ветви:
0 x 4d – ЕВП = ЕНП
Ординаты правой ветви:
6d x 8d – ЕВП
5d x 8d – ЕНП
x = 0: N2 = 0
x = 4d: N2 = 2d/h
x = 5d: N2 = 3d/(2h)
x = 6d: N2= d/h
x = 8d: N2= 0
x = 4d: N2= 2d/h
Л.В. N2
Уравнение
левой ветви
N2 x
2h
Уравнение правой ветви
N2
4d
x
1
h
l
18.
хF=1
Линия влияния усилия
в стержне решётки – раскосе
III
4d
h/2
3
B h/2
A
K3
III
d
d
d
d
d
d
d d
Груз F = 1 слева
от сечения III-III:
F=1
0 x 2d
N1
(ЕВП = ЕНП)
SmK3(прав) = 0
N3
No
K3
Груз F = 1 справа
от сечения III-III:
4d x 8d – ЕВП
3d x 8d– ЕНП
SmK3(прав) = 0:
RB* 12d + N3* h3 –
– F * (x + 4d) = 0
B
Уравнение
левой ветви:
RB= 1* x/l
N 3 3x
2h3
Уравнение
правой ветви:
N3
4d
x
1
h3
l
19.
хF=1
Линия влияния усилия
в стержне решётки – раскосе
III
4d
h/2
3
B h/2
A
Правило:
K3
III
d
d
d
d
d
d
d d
6d/h3
Соединительные
прямые при
ЕНП и ЕВП
Ординаты левой ветви:
0 x 4d – ЕВП = ЕНП
Ординаты правой ветви:
4d x 8d – ЕВП
3d x 8d – ЕНП
Л.В. N3
продолжения
левой и правой
ветвей
пересекаются
под моментной
точкой К3
Уравнение
левой ветви
N 3 3x
2h3
x = -4d:
x = 0: N3 = 0
x = 2d: N3 = -3d/h3 N3= 6d/h3
Уравнение правой ветви
x = 3d: N3= 5d/(2h3)
4d
x
x = 4d: N3= 2d/h3 x = -4d:
N3
1
h3
l
N3= 6d/h3
x = 8d: N3= 0
20.
хF=1
Линия влияния усилия
в одиночной стойке
(подвеске)
h/2
A
d
Случай 1:
груз F = 1 не в узле с
(в любом узле ВП
или узлах НП,
кроме узла с):
N4
Sy = 0
у
B h/2
4
N4 = 0
d
d
c
IV
d
d
1
ЕВП = 0
Случай 2:
груз F = 1
в узле с:
d
d d
Соединительные
прямые при ЕНП
N4
Л.В. N4
Sy = 0
F=1
N4 = 1
у
Правило:
линия влияния
имеет вид
треугольника
с вершиной
под узлом,
к которому
примыкает
одиночный
стержень,
и основанием
в пределах
двух смежных
панелей.
21.
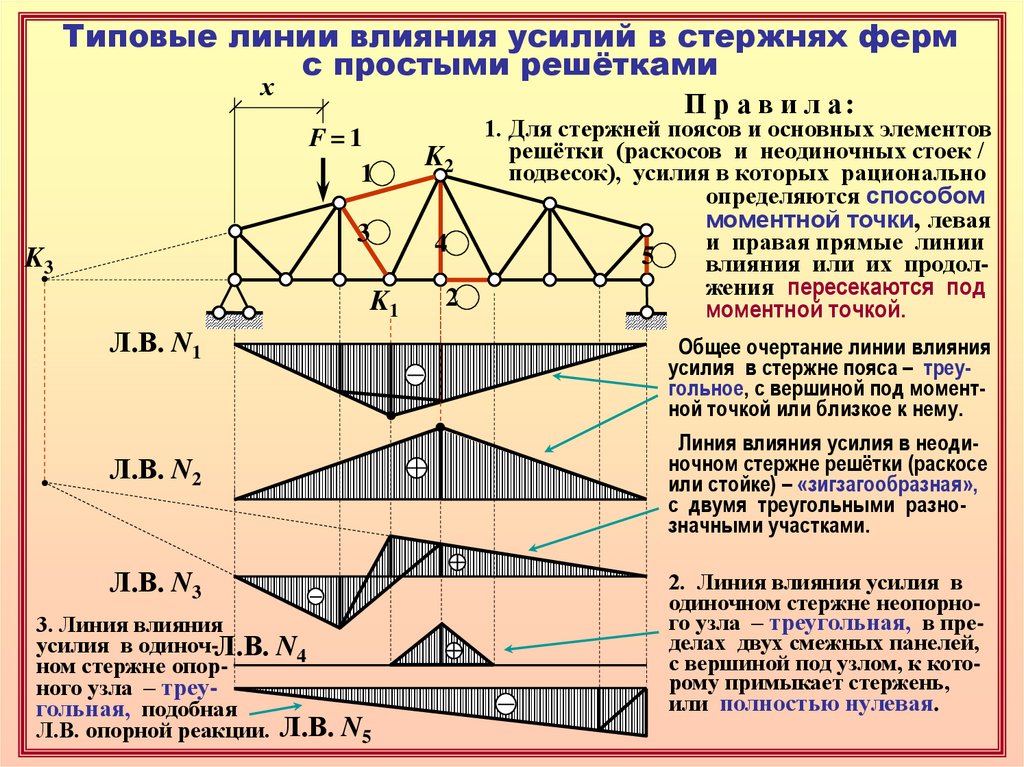
Типовые линии влияния усилий в стержнях фермс простыми решётками
х
П р а в и л а:
F=1
1
K2
3
4
K3
K1
Л.В. N1
Л.В. N2
Л.В. N3
3. Линия влияния
усилия в одиноч-Л.В. N4
ном стержне опорного узла – треугольная, подобная
Л.В. опорной реакции. Л.В. N5
2
1. Для стержней поясов и основных элементов
решётки (раскосов и неодиночных стоек /
подвесок), усилия в которых рационально
определяются способом
моментной точки, левая
и правая прямые линии
5
влияния или их продолжения пересекаются под
моментной точкой.
Общее очертание линии влияния
усилия в стержне пояса – треугольное, с вершиной под моментной точкой или близкое к нему.
Линия влияния усилия в неодиночном стержне решётки (раскосе
или стойке) – «зигзагообразная»,
с двумя треугольными разнозначными участками.
2. Линия влияния усилия в
одиночном стержне неопорного узла – треугольная, в пределах двух смежных панелей,
с вершиной под узлом, к которому примыкает стержень,
или полностью нулевая.










 Механика
Механика








