Алгоритмическая торговля

1.

Алгоритмическая торговля
Научный подход
Введение
Ведущий семинара:
Александр Горчаков

2. Что такое торговый алгоритм (торговая система)?

Начнем с самого общего определения торгового алгоритма.
Определение 1. Торговый алгоритм – это
алгоритм, преобразующий прошлую входящую
информацию в текущее состояние счета.
Т. е. в обывательском смысле – это что-то типа машинки,
печатающей деньги

3. Что мы получаем на выходе торгового алгоритма?

Решение изменить позицию (сигналы о входе в позицию или
выходе из нее) полностью равноценно решению сохранить
позицию, так как именно от этого выбора зависит то будущее
состояние счета, которое мы получим на момент обработки
алгоритмом новой входящей информации.

4. Какой мы хотим видеть эквити счета?

5. От чего зависит эквити счета?

n
S (t ) V (t ) D(t )
i
i 1
i
n
(t 1) V (t ) D(t ),
i 1
i
i
где i (t 1) Si (t 1) Si (t )

6. От чего зависит эквити счета?

Торговый алгоритм
предположения о будущих приращениях цен
торгуемых активов на основе входных данных
выбор оптимальных объемов активов
в рамках этих предположений

7. От чего зависит эквити счета?

i (t 1) Si (t 1) Si (t )
VS
S i (t 1)
hi (t 1) Ln
S i (t )

8. Что можно подавать на вход торгового алгоритма?

Входные данные торгового
алгоритма должны
удовлетворять трем
условиям:
- регулярность;
- достоверность;
- формализуемость.

9. Случайность и детерминированность – Pro et Contra

Приращения логарифмов цен:
• детерминированы, т. е. все будущие
приращения являются функциями от
прошлой информации.
ИЛИ
• случайны, т. е. подавляющее
большинство будущих приращений цен
являются набором значений с
некоторыми вероятностями их
появления, как минимум, две из которых
ненулевые.

10. Торговый алгоритм – это статистический прогноз

Оптимальным прогнозом будущего значения
случайной величины ξ при входной
информации I является случайная величина с
распределением
P ( x, i )
P( x / i )
P (i )
где x – значение из множества возможных
значений случайной величины ξ, а i – значение из
множества возможных значений I.
Приведенное распределение еще называют
условным распределением ξ при условии I и
обозначают как P(ξ/I).
Задача оценки этого распределения и(или) его
отдельных характеристик и называется в теории
вероятностей задачей статистического прогноза.

11. Торговый алгоритм – это статистический прогноз

Предположения
о будущих
приращениях
цен торгуемых
активов
Статистический
прогноз

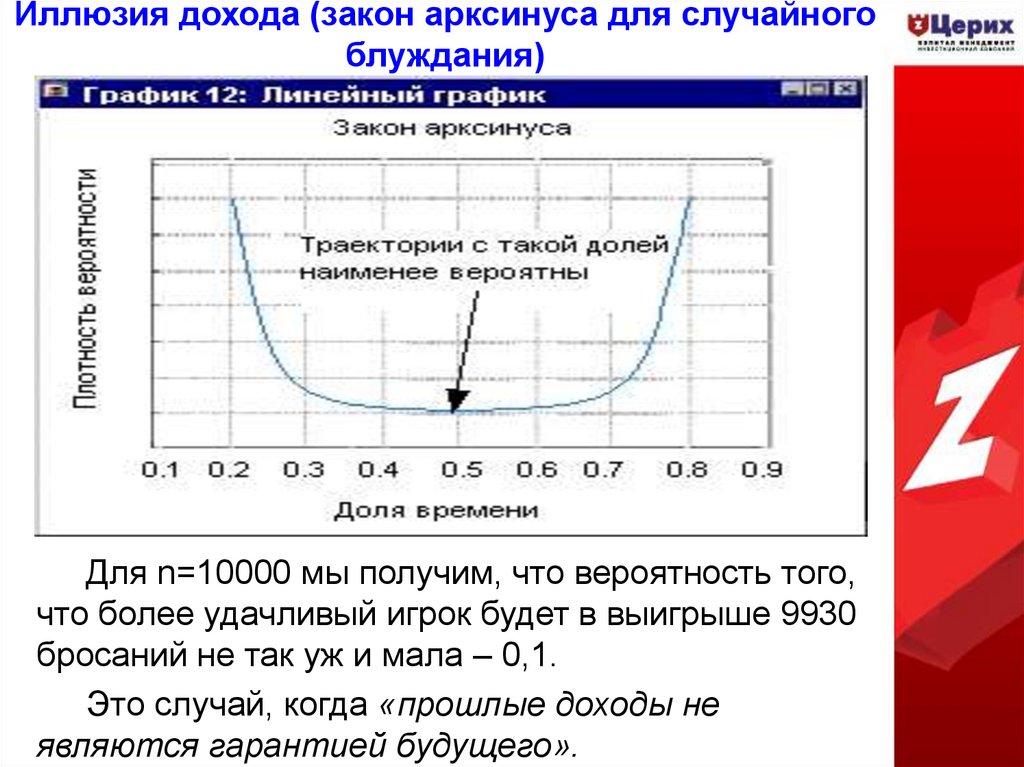
12. Иллюзия дохода (закон арксинуса для случайного блуждания)

rt
h(t )
rt
Статистический прогноз невозможен если
Р(x,i)=P(x)·P(i),
которое означает независимость
случайных величин ξ и I.
Пусть
• rt=const
• P(h(t))=½
• h(t)- независимы

13. Иллюзия дохода (закон арксинуса для случайного блуждания)

Через Σm обозначим частичные суммы h (t) , т. е.
S ( m) m
h(t )
Ln
S 0) t 1
Согласно «закону арксинуса» k - число положительных значений
среди Σm, m=1,…,n, имеет распределение
2k 2(n k ) 1
2 n
P(k )
k (n k ) 2
Откуда следует, что при n→∞ распределение k/n стремится к
непрерывному распределению с плотностью
( x(1 x) ) 1
и функцией распределения
2 1 arcsin
x
давшей название соответствующей теореме.

14. Иллюзия дохода (закон арксинуса для случайного блуждания)

Для n=10000 мы получим, что вероятность того,
что более удачливый игрок будет в выигрыше 9930
бросаний не так уж и мала – 0,1.
Это случай, когда «прошлые доходы не
являются гарантией будущего».

15. Зависимость – основа основ торгового алгоритма

Некорректно!!!
- Использовать прибыль на всем
интервале оптимизации, для отбора
параметров торговых алгоритмов;
- Оценивать эффективность торгового
алгоритма только по превосходству
доходности над доходностью стратегии
«купил и держи».
Построение эффективного торгового
алгоритма возможно тогда и только тогда,
когда существует статистическая
зависимость между прошлыми
входными данными этого алгоритма и
будущим изменением цен торгуемых
активов.

16. Некоторые виды статистических зависимостей

1. Р (h (t) >0)=(1+δm)/2, δm ≠ 0,
h (t) и h (t+1)-независимы,
Р(sign(δm )= sign(δm+1 ))<½,
sign(x )- знак x;
2. Р (h(t) >0)=½,
Р(sign(h (t) )= sign(h (t+1))=(1+δm)/2,
δm ≠ 0.

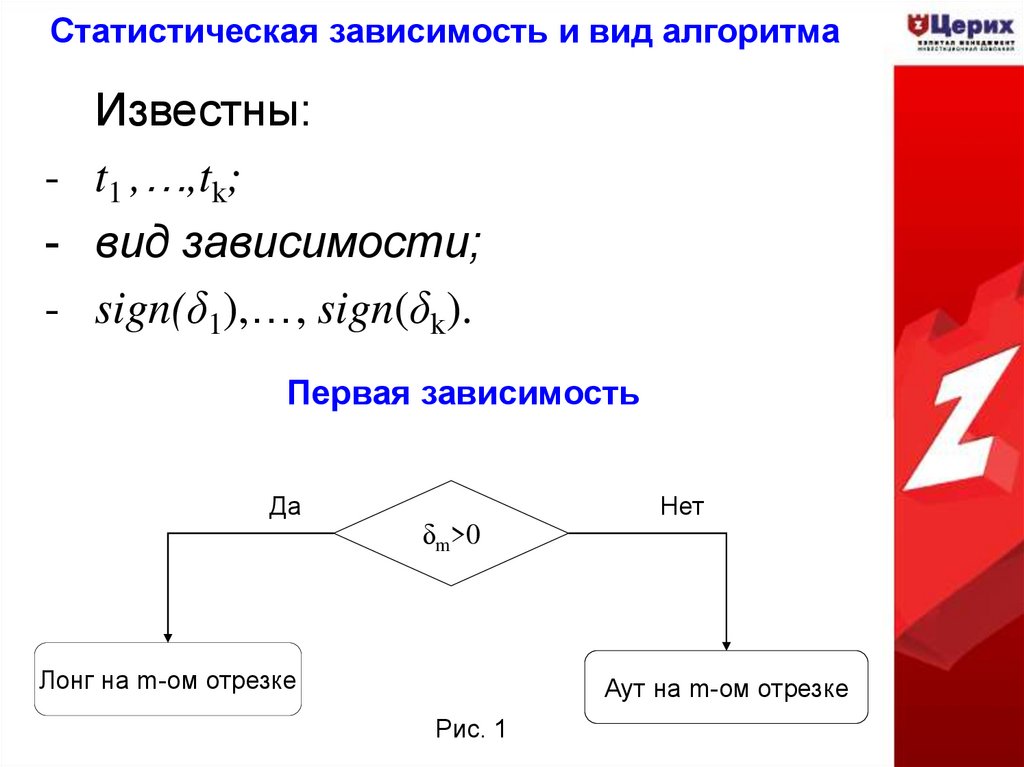
17. Статистическая зависимость и вид алгоритма

Известны:
- t1 ,…,tk;
- вид зависимости;
- sign(δ1),…, sign(δk).
Первая зависимость
Да
δm>0
Лонг на m-ом отрезке
Нет
Аут на m-ом отрезке
Рис. 1

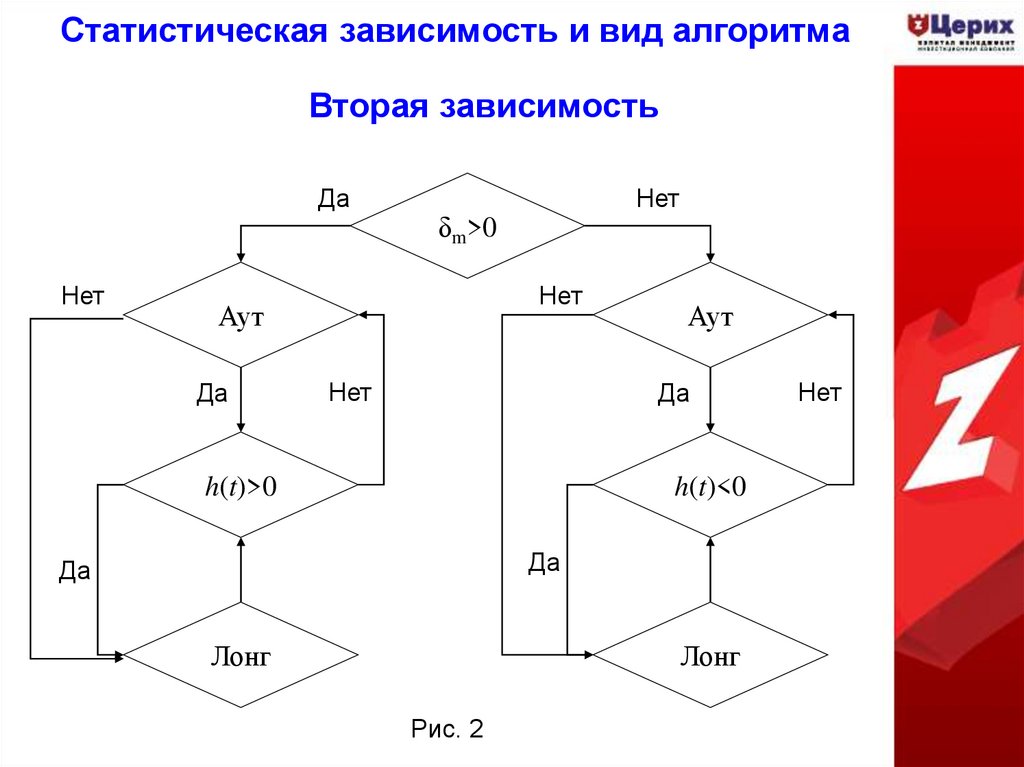
18. Статистическая зависимость и вид алгоритма

Вторая зависимость
Да
Нет
δm>0
Нет
Аут
Да
Нет
Нет
Аут
Да
h(t)>0
h(t)<0
Да
Да
Лонг
Лонг
Рис. 2
Нет

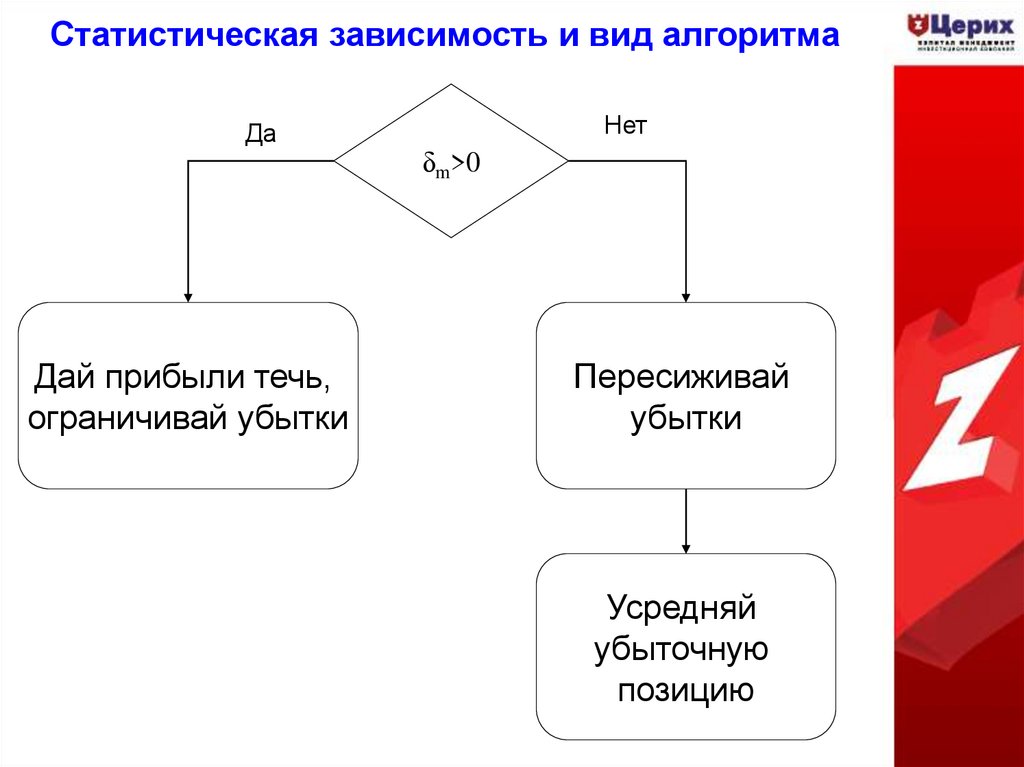
19. Статистическая зависимость и вид алгоритма

Да
Дай прибыли течь,
ограничивай убытки
Нет
δm>0
Пересиживай
убытки
Усредняй
убыточную
позицию

20. Статистическая зависимость и вид алгоритма

δm<0
|h (t)|/k
…
|h (t)|/k
|h (t)|/k
δj>0
Задача построения торгового
алгоритма для антиперсистентного
рынка может быть сведена к задаче
построения торгового алгоритма для
персистентного рынка с более высокой
частотой принятия решения о смене или
сохранении позиции.

21. Статистическая зависимость и вид алгоритма

Задача построения торгового алгоритма
сводится к
• задачам оценки длин отрезков t1 ,…,tk,
• определения вида зависимости
• знака величин δm (в случае
антиперсистентного рынка еще и к оценке
последних значений).
В теории вероятностей эта задача
называется «задачей о разладке». Ее
особенностью для построения торговых
алгоритмов является то, что, как правило, ее
решение приходится искать в условиях
«малых выборок».

22. Краткие выводы

Любой торговый алгоритм является явным или неявным
статистическим прогнозом будущих приращений цен
(логарифмов цен) или функций от них;
Некорректно оценивать эффективность алгоритма только
по одному параметру – доходности за весь период
работы;
Построение торговых алгоритмов возможно только в
условиях наличия зависимости между входной
информацией и приращениями цен (логарифмов цен);
В случаев наличия в приращениях логарифмов цен (или
функций от них) участков со стационарной
персистентностью (антиперсистентностью) задача
построения торгового алгоритма сводится к известной в
теории вероятностей «задаче о разладке» на малых
выборках;
Задача построения торгового алгоритма для
антиперсистентного отрезка рынка может быть сведена к
задаче построения торгового алгоритма для рынка с
персистентными отрезками, но с более высокой частотой
принятия решения о смене или сохранении позиции.

23. «Аксиомы»

• Отбор параметров торговых
алгоритмов должен происходить
на основе анализа свойств
эквити счета, построенной по
тактам, в которые принималось
решение об изменении или
сохранении позиции;
• Торговые алгоритмы «только
лонг» и «только шорт»
анализируются раздельно.

24. Случай одного актива

Эквити счета для i-го
набора значений
параметров (множество
параметров предполагается
конечным)
Эi(t)=Vi(t)·C(t)+Di(t)

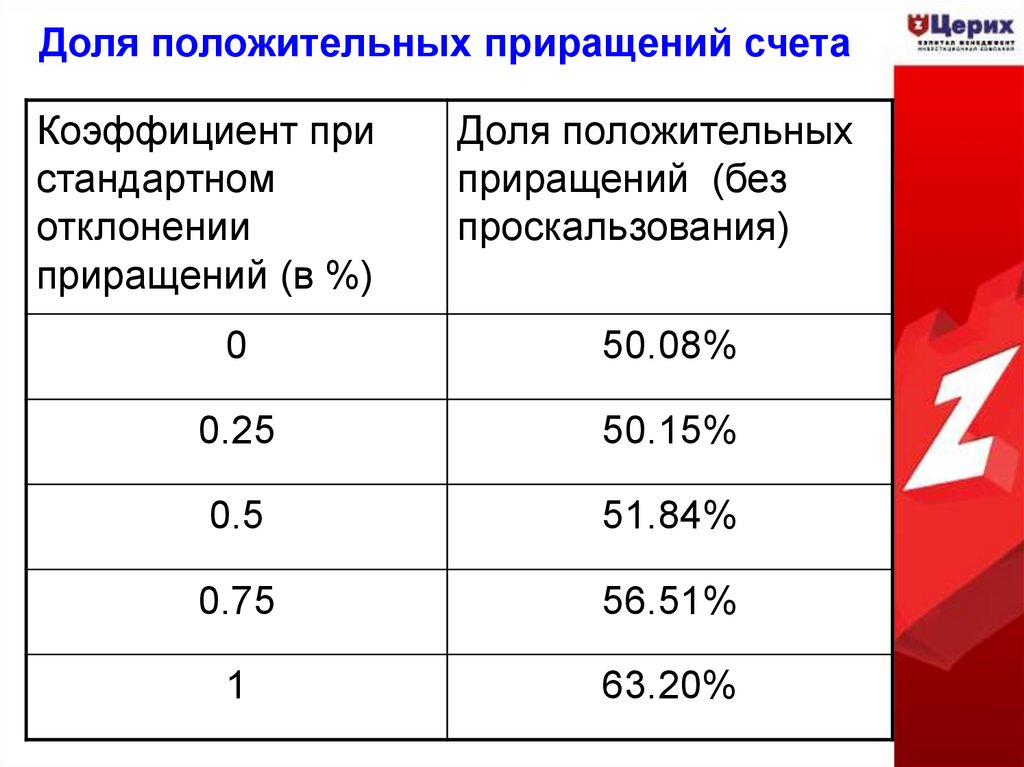
25. Доля положительных приращений счета

Коэффициент при
стандартном
отклонении
приращений (в %)
Доля положительных
приращений (без
проскальзования)
0
50.08%
0.25
50.15%
0.5
51.84%
0.75
56.51%
1
63.20%

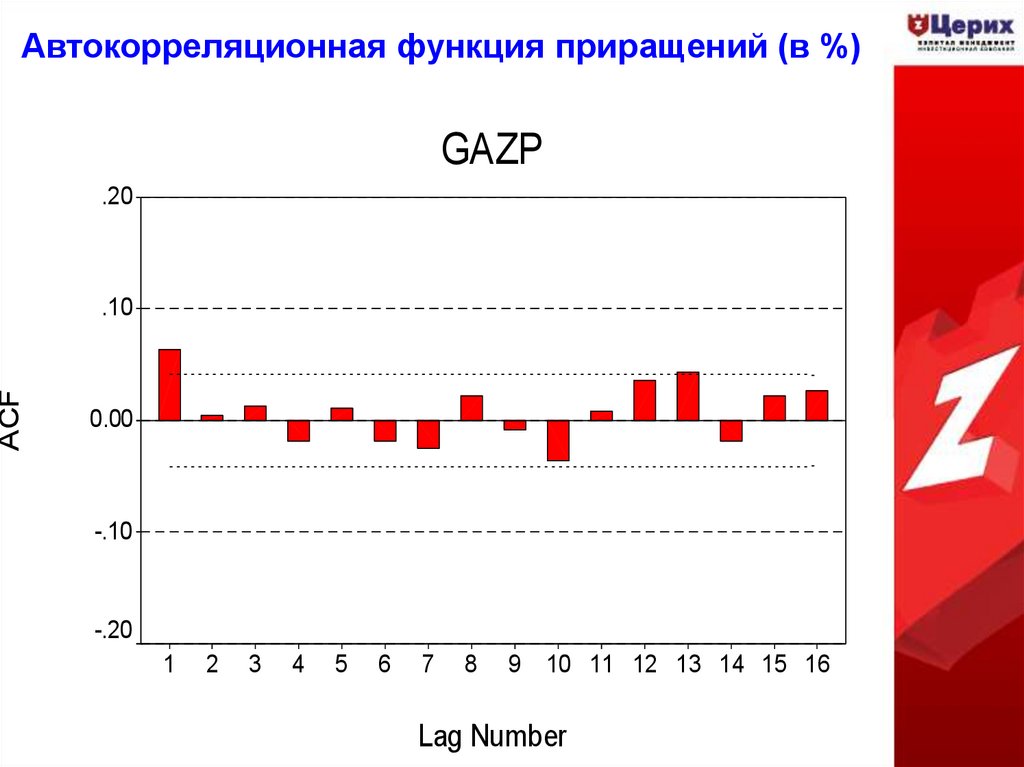
26. Автокорреляционная функция приращений (в %)

GAZP
.20
ACF
.10
0.00
-.10
-.20
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15 16
Lag Number

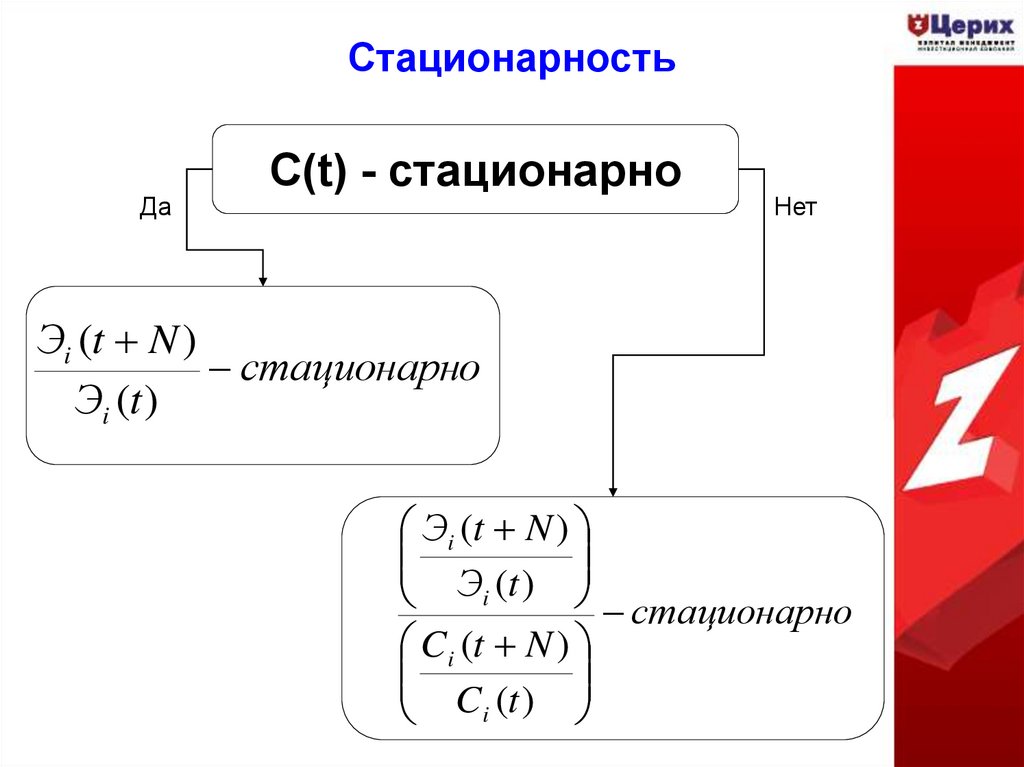
27. Стационарность

Да
С(t) - стационарно
Нет
Эi (t N )
стационарно
Эi (t )
Эi (t N )
Эi (t ) стационарно
Ci (t N )
Ci (t )

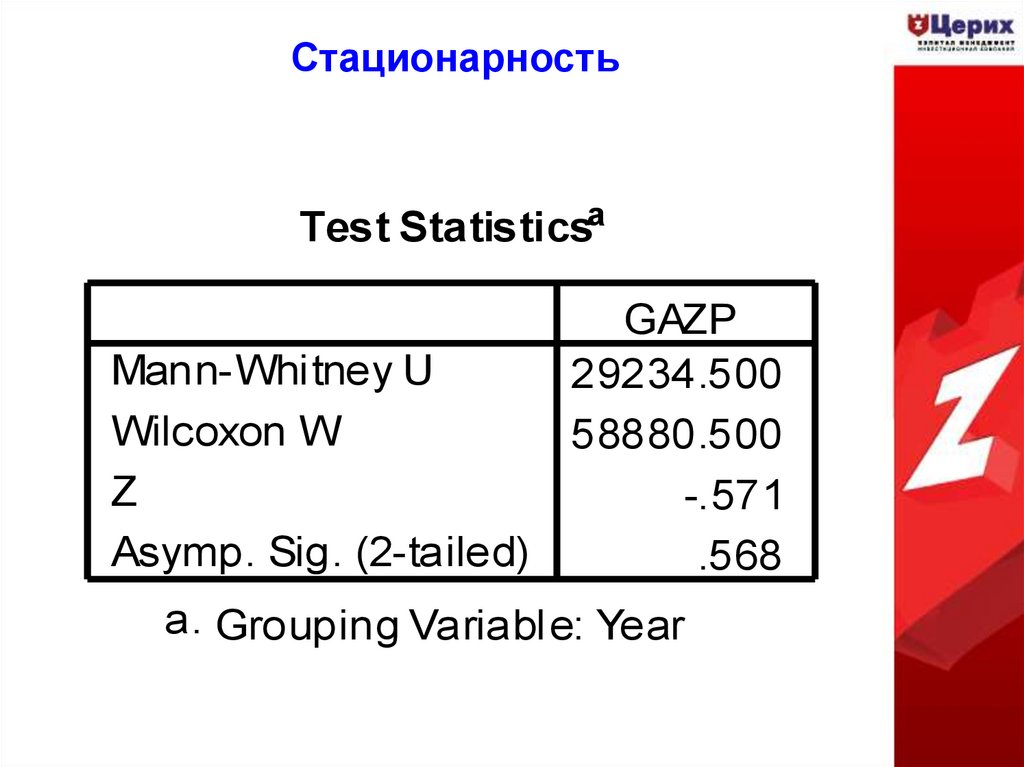
28. Стационарность

Test Statisticsa
GAZP
Mann-Whitney U
29234.500
Wilcoxon W
58880.500
Z
-.571
Asymp. Sig. (2-tailed)
.568
a. Grouping Variable: Year

29. Стохастическое доминирование

I рода. Для любого х
Э j (t N )
Эi (t N )
P(
x) P(
x)
Эi (t )
Э j (t )
II рода. Для любого х
Э j (t N ) Э j (t N )
Эi (t N ) Эi (t N )
I (
I (
E
x) E
x)
Э (t ) Э (t )
Э (t ) Э (t )
i
j
i
j

30. Корреляционный анализ

Эi (t 1)
M (t 1) MAX
i
Эi (t )
Строим линейную регрессию методом
включения-исключения
Эi (t 1)
M (t 1) ai
b(t 1)
Эi (t )
i

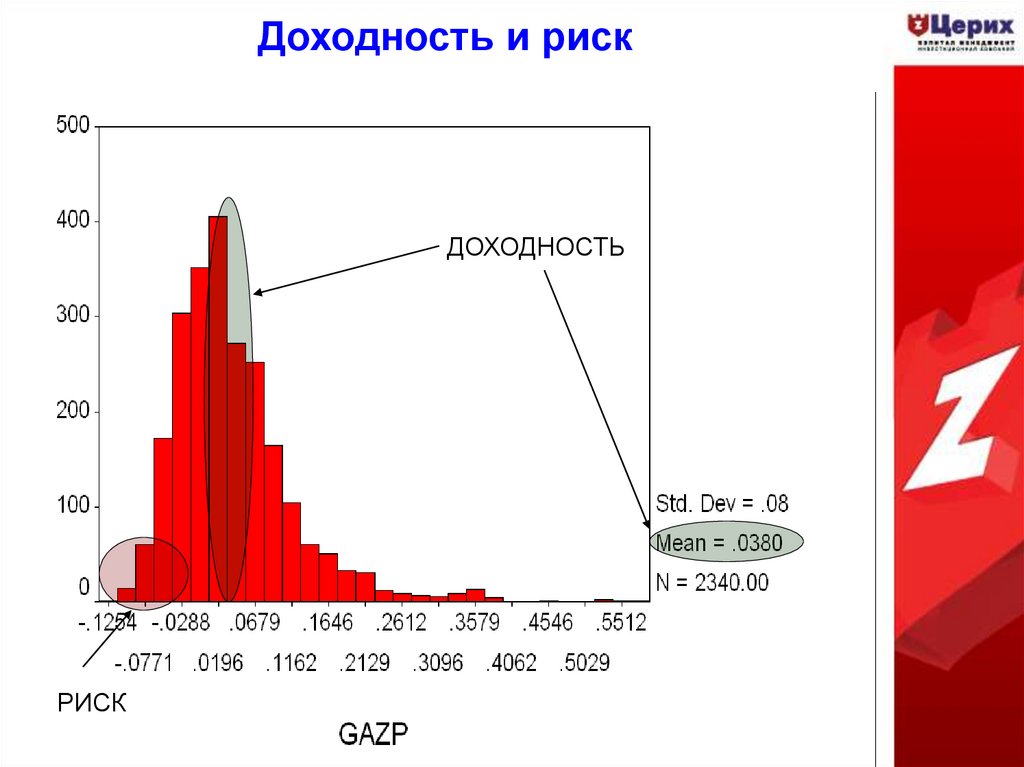
31. Доходность и риск

ДОХОДНОСТЬ
РИСК

32. Доходность и риск

• Доходность (Di)
Эi (t N )
1
E
Эi (t )
• Риск (Ri)
Эi (t N )
1)
n%CVAR(
Эi (t )
– среднее n% наименьших значений
Эi (t N )
1
Эi (t )
n% - такое, что Ri меньше нуля для
любой из неотсеянных систем.

33. Доходность и риск

Соотношение «доходностьриск» i-ого торгового алгоритма
Di+λRi, 0<λ<1
λ – определяется
толерантностью к риску.
D+(R+) – доходность (риск)
стратегии «купил и держи»
D-(R-) – доходность (риск)
стратегии «продал и жди»

34. Доходность и риск

• Для «только лонг»
Di+λRi> D++λR+
• Для «только шорт»
Di+λRi> D-+λR-

35. Оптимизация

Э(t , a ) ai Эi (t ), 0 ai 1, ai 1
i
i
Э(t N , a )
D( a ) E
1
Э (t , a)
Э(t N , a )
R( a ) n%CVAR(
1
)
Э(t , a)
D( a ) R( a ) max
a

36. Округление

a max a i
i
wi
1
a
g
ai
, где g ( x) округление до целого числа
wi , если wi 0.1
ri
0, в противном случае
di
ri
ri
i

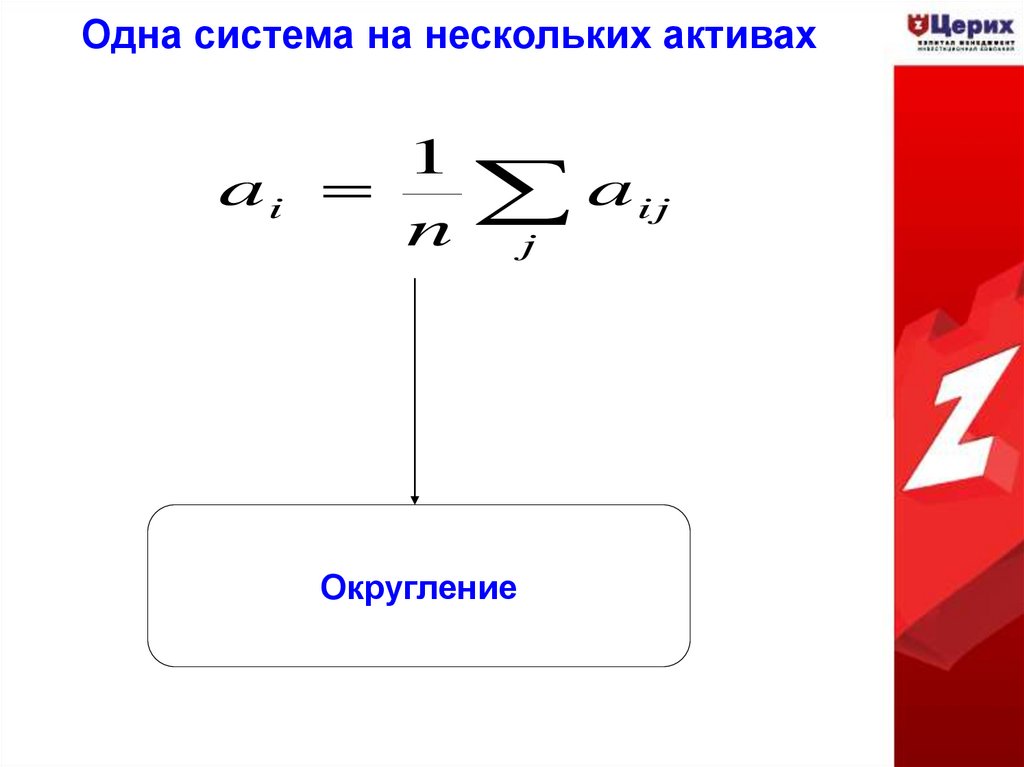
37. Одна система на нескольких активах

ai
1
a ij
n j
Округление

38. Портфель систем

Цели
• Улучшение соотношения
«доходность-риск»;
• Уменьшение
проскальзования;
• Увеличение «емкости»
торгового алгоритма.

39. Портфель систем

Группировка
Корреляционный анализ
Оптимизация
Округление

40. Выбор плеча (метод Монте-Карло)

DD (>0) – допустимая просадка
счета.
Э(t 1)
1
(t 1)
Э(t )
1, 2 , T
, 1 ni T
П j
n1 , n2 , nT
t 1
Э j (t 1) (1 (ni ))
i 1

41. Выбор плеча (метод Монте-Карло)

Пусть j=1,…,M, M≥100.
MAXDrDwj (>0) – максимальная
просадка «счета», построенная по
«эквити» Эj(t+1).
MAXDrDw max MAXDrDw j
j
DD
1,
MAXDrDw
размер кредитного плеча