Похожие презентации:
3 Преобразование случайных величин
1. Тема 3 Преобразование случайных величин
«Всякий, кто питает слабость к арифметическим методамполучения случайных чисел, грешен вне всяких сомнений»
Джон фон Нейман
2.
Процесс нахождения значенияслучайной величины путем
преобразования стандартной случайной
величины (БСВ) называют
разыгрыванием или моделированием
случайной величины .
2
3. Метод обратного преобразования (обратной функции)
Пусть необходимо получать значения случайнойвеличины , являющейся непрерывной и имеющей
функцию распределения 0<F(x)<1 непрерывную и
строго возрастающую.
F-1 – обратная функция F.
Алгоритм генерирования СВ с функцией распределения F:
1) генерируем ;
2) возвращаем = F-1( ).
3
4. Использование функции плотности вероятности
• нужно получать значения случайной величины ,распределенной в интервале (a, b) с плотностью
f(х)>0.
Достоинство:
• точность метода.
f ( x)dx
a
Недостатки:
• ограничение на вид функции распределения или
функции плотности;
• затраты машинного времени.
4
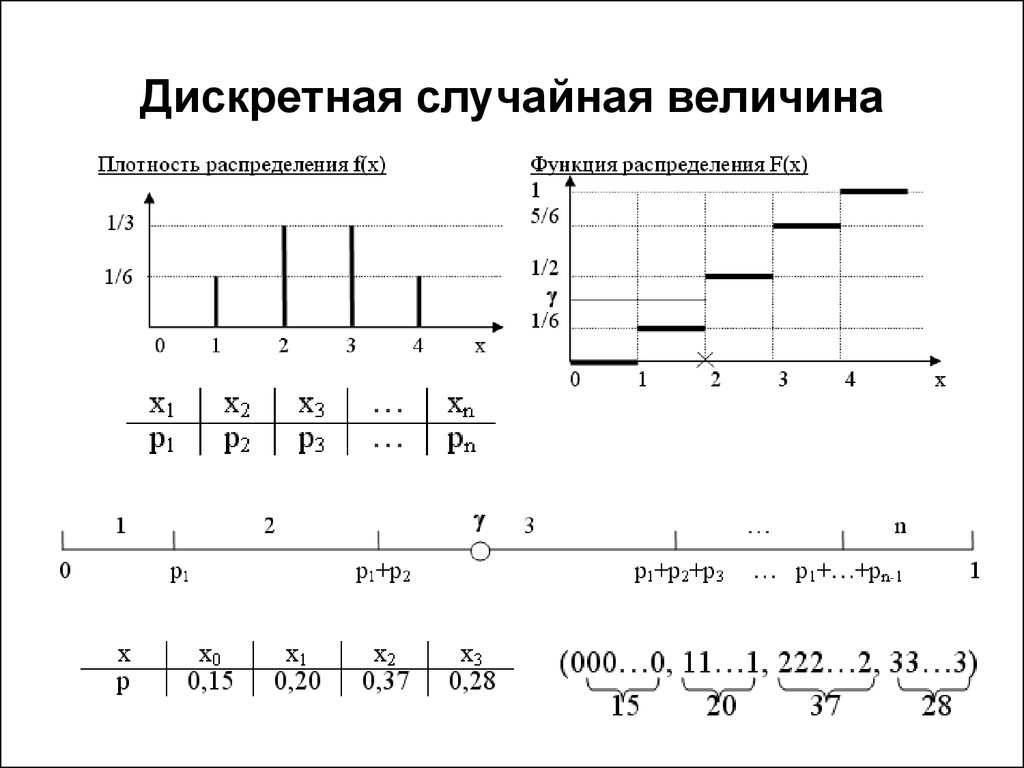
5. Дискретная случайная величина
56. Метод отбора-отказа (метод Неймана, 1951)
Разыгрывать можно следующим способом:1) H(t1,t2) с координатами: t1 = a+ 1(b-a); t2 = 2M0;
2) если H(t1,t2) лежит под кривой f(x), то полагаем =t1, иначе – пару
( 1, 2) отбрасываем и выбираем новую пару значений БСВ.
6
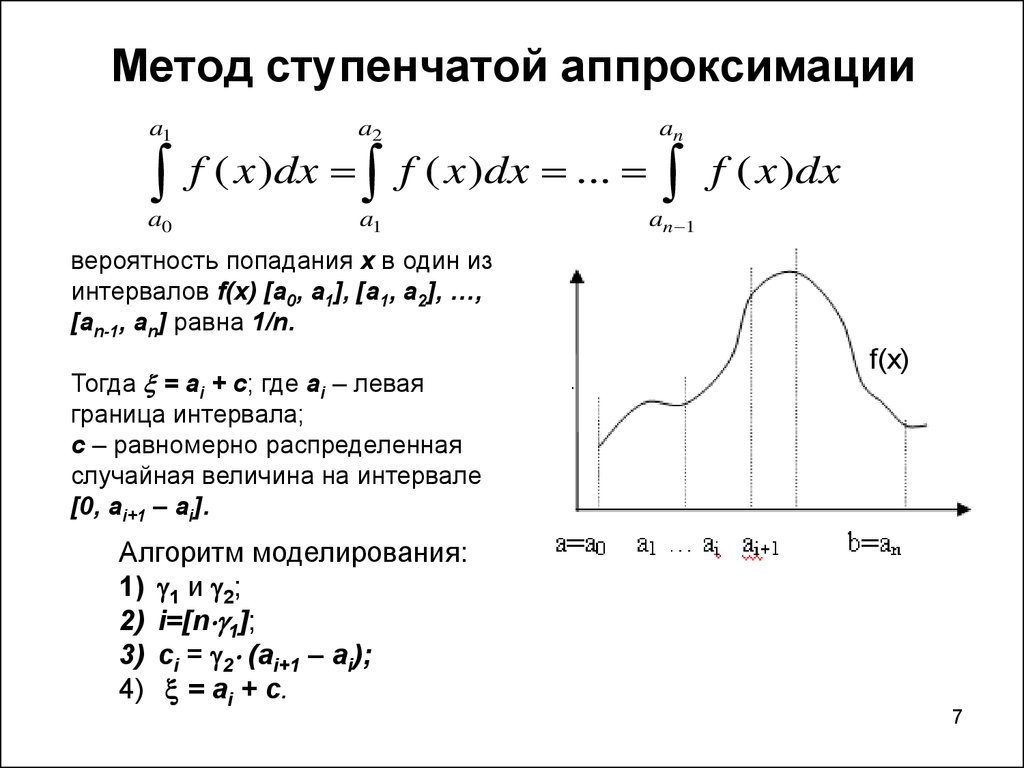
7. Метод ступенчатой аппроксимации
a1a0
a2
f ( x )dx f ( x )dx ...
a1
an
f ( x )dx
an 1
вероятность попадания х в один из
интервалов f(x) [a0, a1], [a1, a2], …,
[an-1, an] равна 1/n.
Тогда = ai + c; где ai – левая
граница интервала;
с – равномерно распределенная
случайная величина на интервале
[0, ai+1 – ai].
f(x)
Алгоритм моделирования:
1) 1 и 2;
2) i=[n 1];
3) сi = 2 (ai+1 – ai);
4) = ai + c.
7
8. Пример: Пусть задана функция плотности распределения непрерывной случайной величины f(х)=sin(x), на интервале [0, 90]. Составить алгоритм модел
Пример: Пусть задана функция плотности распределения непрерывнойслучайной величины f(х)=sin(x), на интервале [0, 90 ]. Составить алгоритм
моделирования случайной величины методом ступенчатой аппроксимации
для трех интервалов разбиения.
Так как 3 интервала разбиения, то вероятность равна 1/3.
а0=0; а3=90 ; а1 находим из выражения
a1
1
1
a
a sin xdx 3 ; cos x 0 cosa1 1 3
1
0
отсюда a1=arcos2/3= 0 .
а2 находим аналогично
a2
1
2 1
a
sin
xdx
;
cos
x
cos
a
cos
a
cos
a
а
2
1
2
a
3
3 3
2
1
1
a2=arcos 1/3 = 70 .
Далее применяем алгоритм моделирования.
8
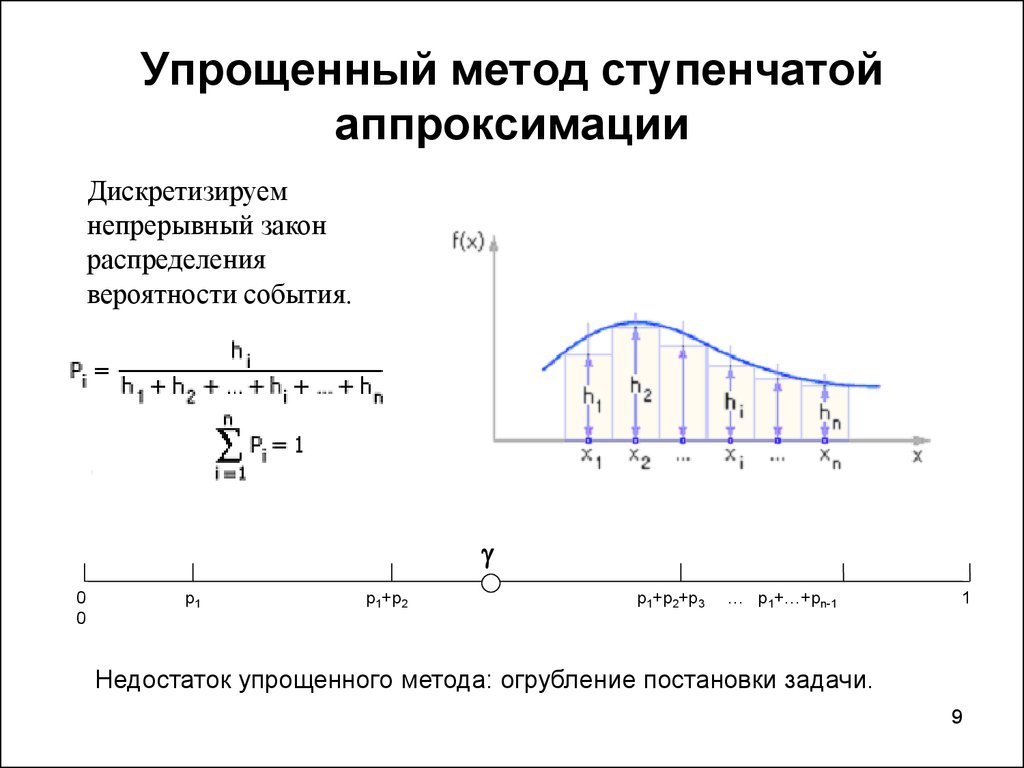
9. Упрощенный метод ступенчатой аппроксимации
Дискретизируемнепрерывный закон
распределения
вероятности события.
0
0
р1
р1+р2
р1+р2+р3
… р1+…+рn-1
1
Недостаток упрощенного метода: огрубление постановки задачи.
9
10. Метод суперпозиции
Функция распределения F может быть выражена как комбинациядругих функций F1, F2,…
F ( x) pi Fi ( x),
i 1
p
i 1
i
1
, и соответственно
f ( x) pi f i ( x)
i 1
Общий алгоритм метода суперпозиции примет следующий вид:
1) генерируем положительное целое число i=1, 2, …
2) возвращаем с функцией распределения
Fi (x) .
Шаг 1 можно рассматривать как выбор функции распределения Fi с
вероятностью pi.
10
11. Метод сверток
Пример: нормальное (Гауссово) распределениеЦентральная предельная теорема
Пусть СВ x подчинены одному и тому же закону распределения, с
одним и тем же математическим ожиданием Mx и дисперсией Dx=σx2.
Тогда сумма n этих СВ будет подчинена нормальному закону
распределения с математическим ожиданием M=n∙Mx и дисперсией
D=n∙σx2.
Пусть надо получить нормально распределенный ряд чисел X с заданным
математическим ожиданием Mx и стандартным отклонением σx:
x
n
X Mx
i n / 2
n / 12 i 1
при n=12
12
X M x x i 6
i 1
11
12. Табличный метод
Таблица: функция распределения F(х) и соответствующее емузначение x случайной величины.
Значение случайного числа, находящегося между узлами табуляции,
обычно рассчитывается методом линейной интерполяции.
Представленные в таблице значения соответствуют экспоненциальному
распределению с математическим ожиданием, равным единице.
12
13. Метод композиций
• Метод композиций основан на функциональных особенностяхвероятностных распределений, таких как распределение Эрланга,
гипоэкспоненциальное и гиперэкспоненциальное распределения.
• Метод используется, как правило, в тех случаях, когда не удаётся
получить аналитическим методом решение в явном виде.
• Например, значения случайных величин, распределённых по закону
Эрланга и гипоэкспоненциальному закону могут быть получены путём
сложения нескольких экспоненциально распределённых случайных
величин, а значения случайных величин, распределённых по
гиперэкспоненциальному закону – путём вероятностного формирования
смеси из нескольких экспоненциально распределённых случайных
величин с разными математическими ожиданиями.
13
14. Моделирование событий
Моделирования события А с вероятностью Р(А):P(A).
Моделирование полной группы случайных событий
Пусть независимые события А и В могут появляться одновременно и
имеют вероятности Р(А) и Р(В) соответственно. Возможные исходы:
АВ, AB, AB, A B
(*)
Моделирование таких испытаний может быть осуществлено 2 способами.
1. 1 и 2 и проверка: 1 P(A) и 2 Р(В).
2. Моделированию события с четырьмя возможными исходами с
вероятностями (*). Интервал [0,1] разбивается на четыре части в
соответствии с выписанными вероятностями, генерируется одна случайная
величина и проверяется, в какой из полученных интервалов она попадет.
14
15. Моделирование событий
Моделирование появления зависимых событийПусть заданы вероятности Р(А) и Р(В) зависимых событий А и В и
условная вероятность Р(В|А). Возможны два подхода:
1. Генерируется СВ 1 и проверяется выполнение неравенства 1<=P(A).
Вырабатывается СВ 2 и проверяется неравенство 2<=P(В|А). Проверка
этих неравенств дает нам исходы АВ и А В .
Если оказалось что 1>P(A), то событие А не произошло и для
моделирования события В нам нужна условная вероятность P(B| А ).
Формула полной вероятности (Формула Бейеса):
15
16. Моделирование событий
2. Генерируется одна случайная величина и проверяется, в какой изинтервалов она попадает. Интервалы определяются в соответствии с
вероятностями:
16
17. Моделирование случайных векторов
1. Независимые координаты векторах1, х2, … хn; f(x1, x2,…xn); f(x1, x2,…xn) = f1(x1) f2(x2)… fn(хn)
Значение каждой координаты с плотностью распределения fi(хi)
определяется независимо друг от друга по любой из методик
моделирования значений СВ.
2. Зависимые координаты вектора
Тогда f(x1, x2,…xn) = f1(x1) f2(x2|x1) f3(x3|x1x2)…, где fi есть условная
плотность распределения данной случайной величины xi при условии,
что другие случайные координаты приняли определенные значения.
Алгоритм моделирования значения случайного вектора с зависимыми
координатами предусматривает: получение значения x1, полученное
значение берется в качестве параметра в условной плотности f2(x2|x1),
после чего определяется значение случайной координаты x2 и
полученные значения х1 и х2 берутся в качестве параметров в условной
плотности f3(x3|x1x2) и т.д.
17
18. Моделирование случайных векторов
Пример: пусть случайный вектор W имеет две координаты х1 и х2,являющиеся СВ: f1(x1) = 2x1; 0<x1<1. Определить алгоритм моделирования.
Координата х2 распределена равномерно на участке длиной 2 с центром
в точке х1, т.е.
0, если x2 x1 1 или x2 x1 1;
f 2 ( x2 | x1 )
1 / 2, если или x1 1 x2 x1 1.
Решение:
x1
2 x dx
1
1
x1 , 0 x1 1; x1 1 ; x1 1 .
2
2
0
x2
1 / 2dx
2
1 / 2( x2 x1 1) 1 / 2( x2 1 1) 2
x1 1
x2 2 2 1 1 при x1 1 x2 x1 1.
18
19. Моделирование закона распределения Пуассона
• Закон Пуассона описывает число событий, происходящих заодинаковые промежутки времени, при условии независимости
этих событий.
• Для генерирования чисел, соответствующих закону
распределения Пуассона, вычисляется
F(x) для х=0, 1, 2, …N, где N достаточно велико.
x
F ( x)
i 0
i e
i!
, 0
– среднее (мат.ожидание)
• Положим = х, если F(x) F(x+1), где – равномерно
распределенная СВ.
19





![Пример: Пусть задана функция плотности распределения непрерывной случайной величины f(х)=sin(x), на интервале [0, 90]. Составить алгоритм модел Пример: Пусть задана функция плотности распределения непрерывной случайной величины f(х)=sin(x), на интервале [0, 90]. Составить алгоритм модел](https://cf.ppt-online.org/files/slide/o/OSpaAKIDXk7fbhtEvxJec10jPCiFgynN9QwUur/slide-7.jpg)










 Математика
Математика Информатика
Информатика








