Электрические цепи однофазного переменного тока

1. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ОДНОФАЗНОГО ПЕРЕМЕННОГО ТОКА

2. 3. Цепь однофазного тока с ёмкостью, цепь с активным сопротивлением и емкостью, цепь с активным сопротивлением, индуктивностью

и
емкостью.
Резонанс напряжений.

3.

Цепь однофазного переменного тока с
емкостью
• При включении конденсатора
емкостью С под постоянное
напряжение U он заряжается и на его
обкладках накапливаются равные, но
противоположные по знаку количества
электричества.
• Если заряженный конденсатор
отключить от источника тока, то он,
сохраняя заряд, будет обладать
некоторым напряжением UC.

4.

Соединив обкладки заряженного
конденсатора между собой через
сопротивление R, конденсатор,
разряжаясь, дает кратковременный
ток через сопротивление R.

5.

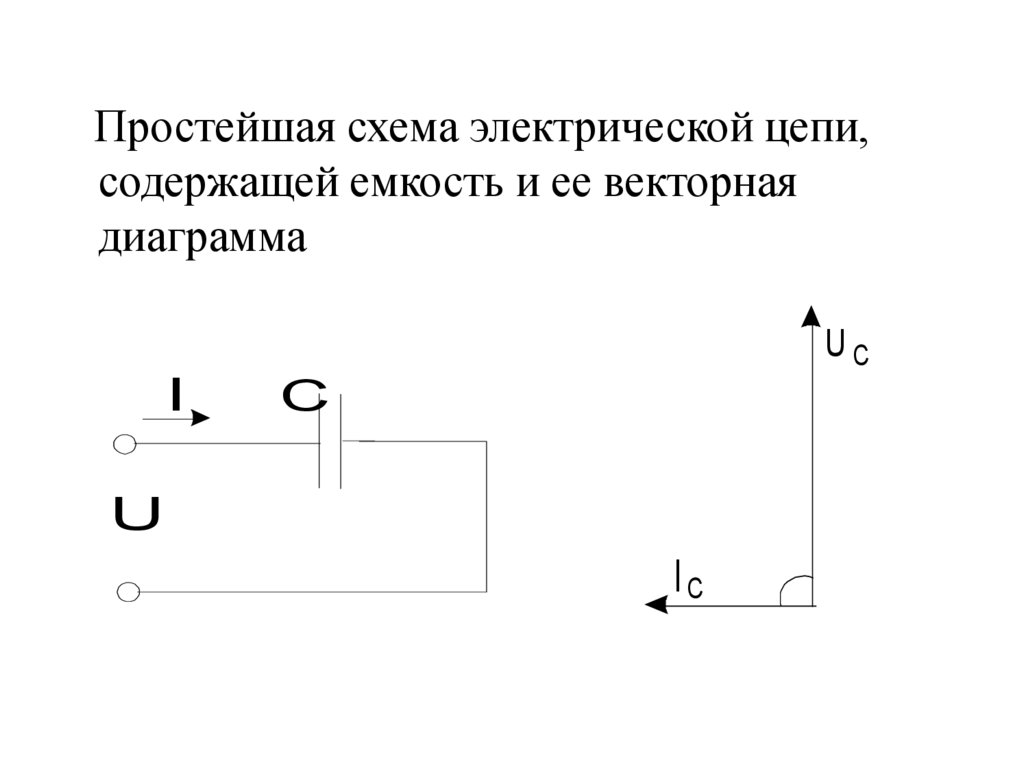
Простейшая схема электрической цепи,
содержащей емкость и ее векторная
диаграмма
I
UC
C
U
IC

6.

Закон Ома для цепи, содержащей емкость,
имеет вид:
UC
I
XC
XC – емкостное сопротивление, Ом
1
1
XC
C 2 fC
C – емкость конденсатора, Ф

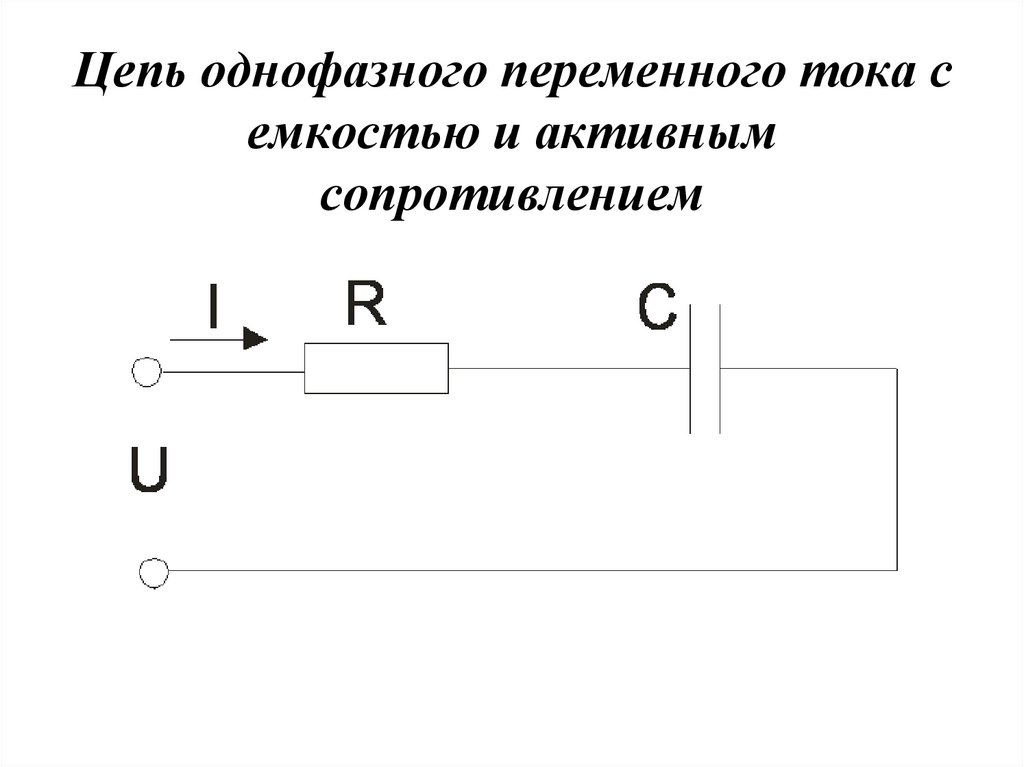
7. Цепь однофазного переменного тока с емкостью и активным сопротивлением

8.

• Ток, проходя по активному
сопротивлению, создает падение
напряжения UR = IR.
• Поскольку рассматриваемая цепь
обладает также и емкостным
сопротивлением XC = 1/ C, то ток I,
проходя через конденсатор, создает
напряжение UС = IХС, которое
называется емкостным падением
напряжения.

9.

Напряжение на конденсаторе
отстает по фазе от тока в нем на
угол 900.
Поэтому на векторной диаграмме
вектор UС будет под углом 900 в
сторону отставания (по часовой
стрелке).

10.

11.

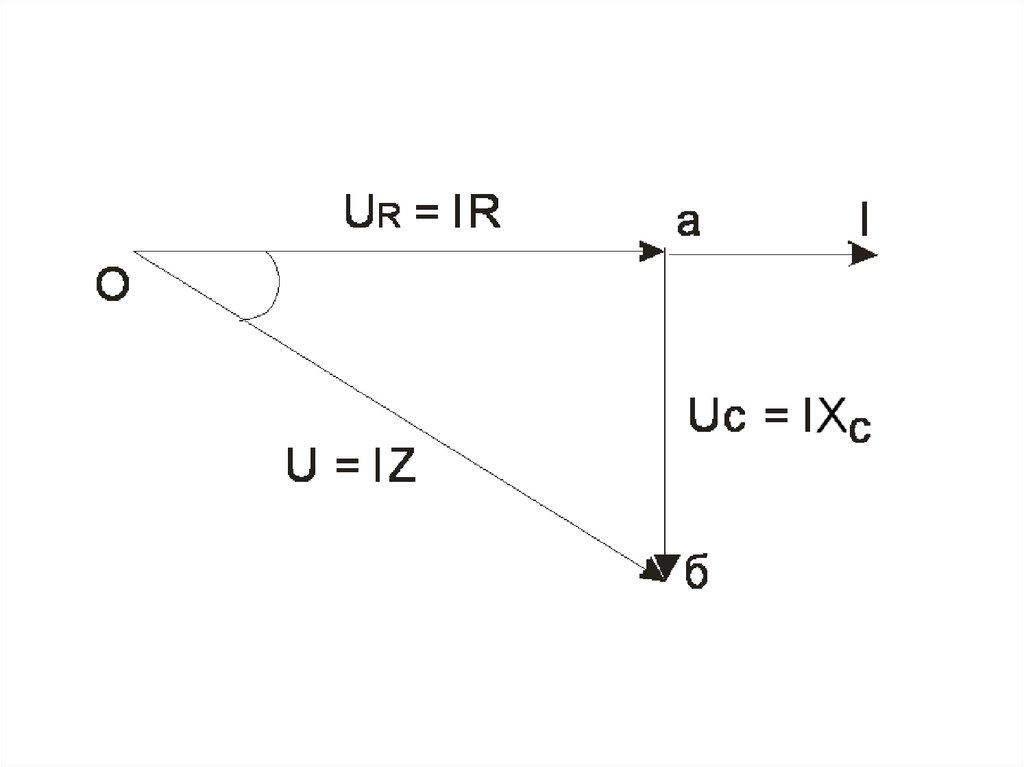
Вектор I опережает вектор U на
некоторый угол φ. Кроме того, вектор
U является гипотенузой
прямоугольного треугольника Оаб,
называемого треугольником
напряжений. Катет треугольника Оа
= UR, а катет аб = UС. То есть
U U R U C ( IR ) ( IX C )
2
2
2
I (R X C )
2
2
2
2
2

12.

Извлекая квадратный корень из обеих
частей выражения, находим, что
U I R XC
2
откуда
I
2
U
R X
2
2

13.

Знаменатель в данном выражении
обозначается Z и называется полным
сопротивлением цепи
Z R X C R (1 C )
2
2
2
2

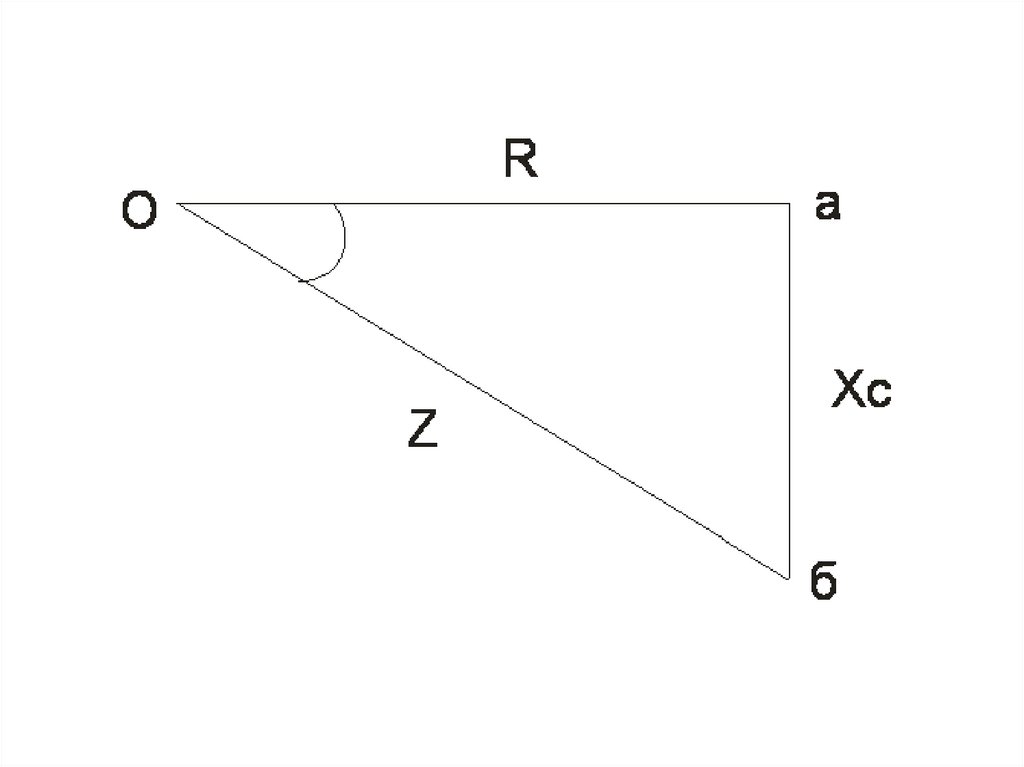
14.

Используя это равенство, можно
построить прямоугольный
треугольник с катетами R и ХС и
гипотенузой Z, называемый
треугольником сопротивлений цепи,
содержащей активное и емкостное
сопротивления

15.

16.

Из треугольника можно определить
косинус угла сдвига фаз φ между
напряжением, приложенным к цепи
и током в ней
R
cos
Z
R
1 2
R (
)
C
2

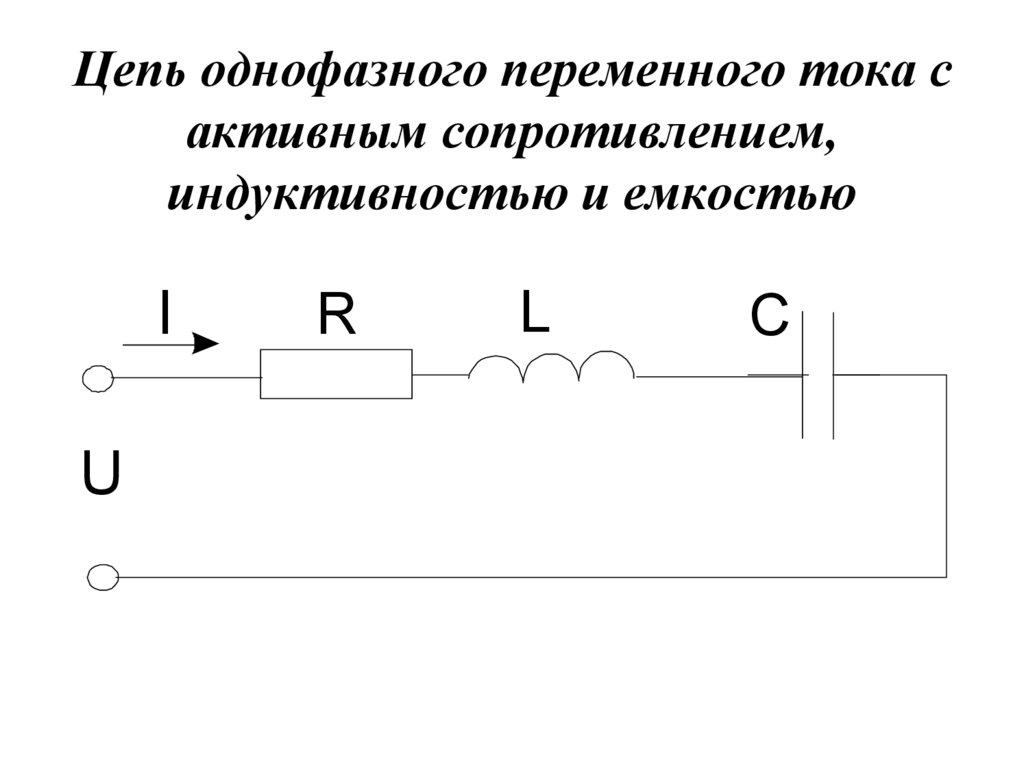
17. Цепь однофазного переменного тока с активным сопротивлением, индуктивностью и емкостью

I
U
R
L
C

18. Цепь однофазного переменного тока с активным сопротивлением, индуктивностью и емкостью

Здесь возможны три случая:
U L UC
U L UC
U L UC

19. Цепь однофазного переменного тока с активным сопротивлением, индуктивностью и емкостью

Рассмотрим случай 1.
Так как напряжение сети
U U R U L UC
то изобразим данные напряжения
векторами и сложим их по правилам
векторного сложения.

20.

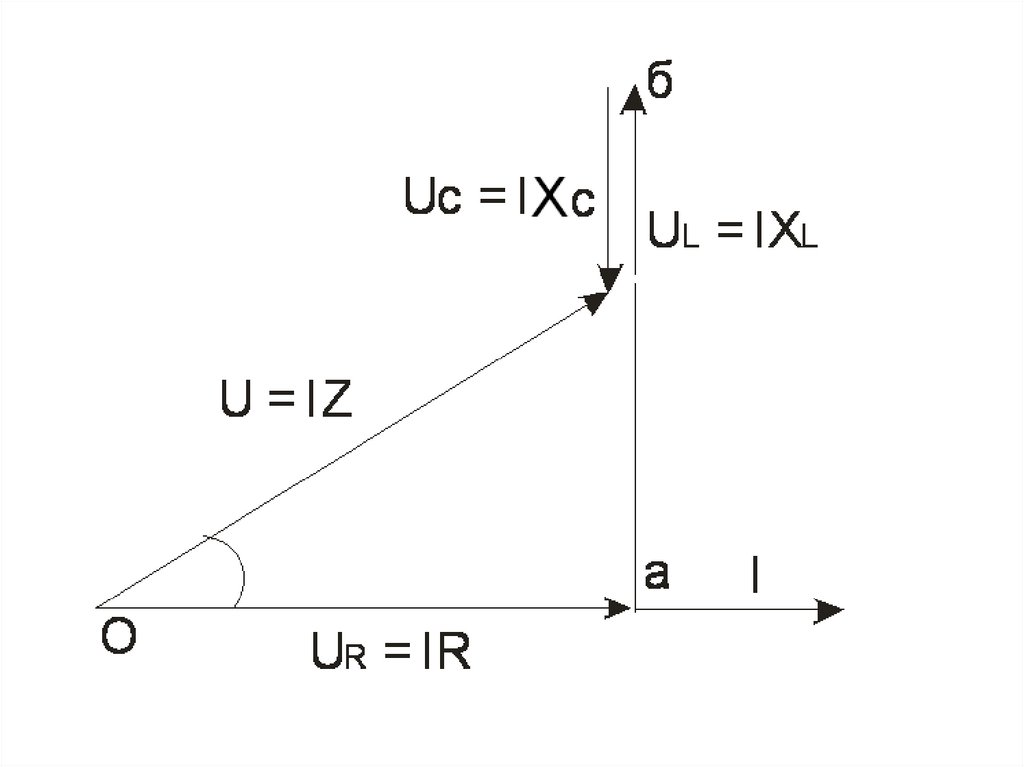
21.

• Прямоугольный треугольник Оаб
называется треугольником напряжения
для цепи, содержащей активное,
индуктивное и емкостное
сопротивления, соединенные
последовательно.
• Катет аб представляет собой разность
индуктивного и емкостного
напряжений и называется реактивным
напряжением для указанной цепи.

22.

Поэтому можно записать:
U U (U L U C )
2
2
R
1
2
I R ( L
C
2
2
2
1
U I R L
C
2
2

23.

U
I
1
R L
C
2
2
Данная формула представляет собой
выражение закона Ома для цепи
переменного тока, содержащей
активное, индуктивное и емкостное
сопротивления.

24.

Знаменатель в этом выражении
представляет собой полное
сопротивление Z для данной цепи
1
Z R L
C
2
2

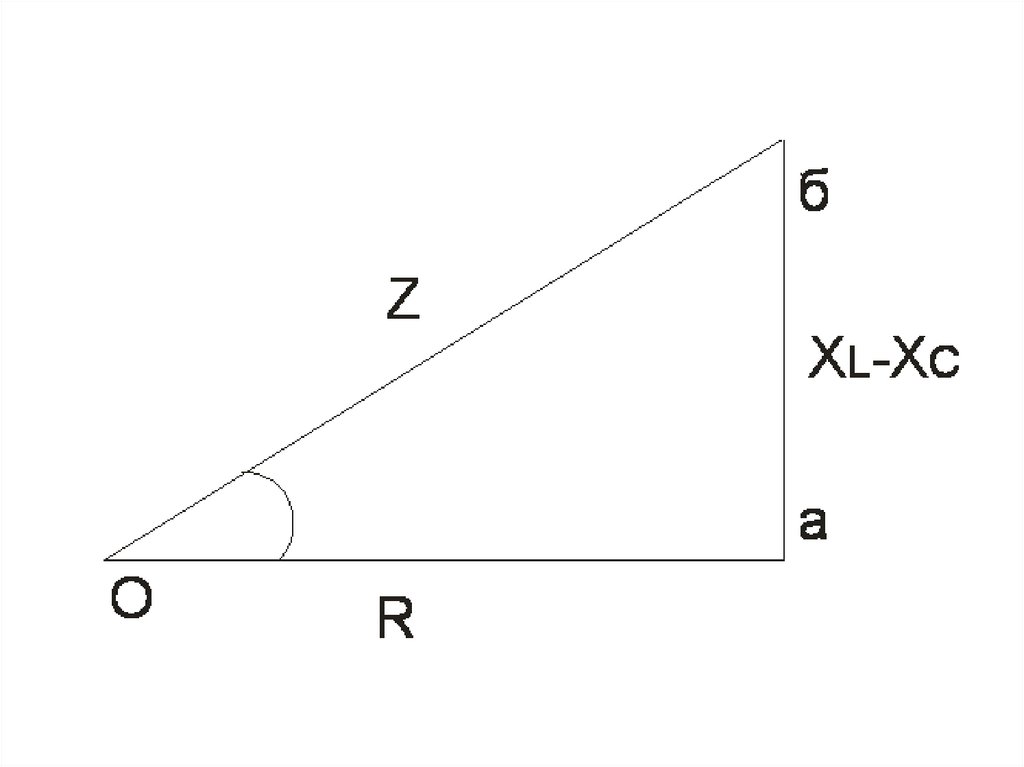
25.

Основываясь на данном равенстве,
можно построить прямоугольный
треугольник сопротивлений для
цепи, содержащей активное
сопротивление, индуктивность и
емкость

26.

27.

Из треугольника сопротивлений
можно определить косинус угла
сдвига фаз между током и
напряжением
R
cos
Z
R
1
R L
C
2
2

28.

Рассмотрим частный случай (3)
последовательного включения
активного, индуктивного и емкостного
сопротивлений, когда разность
индуктивного и емкостного
напряжений равна нулю,
или UL = UC.

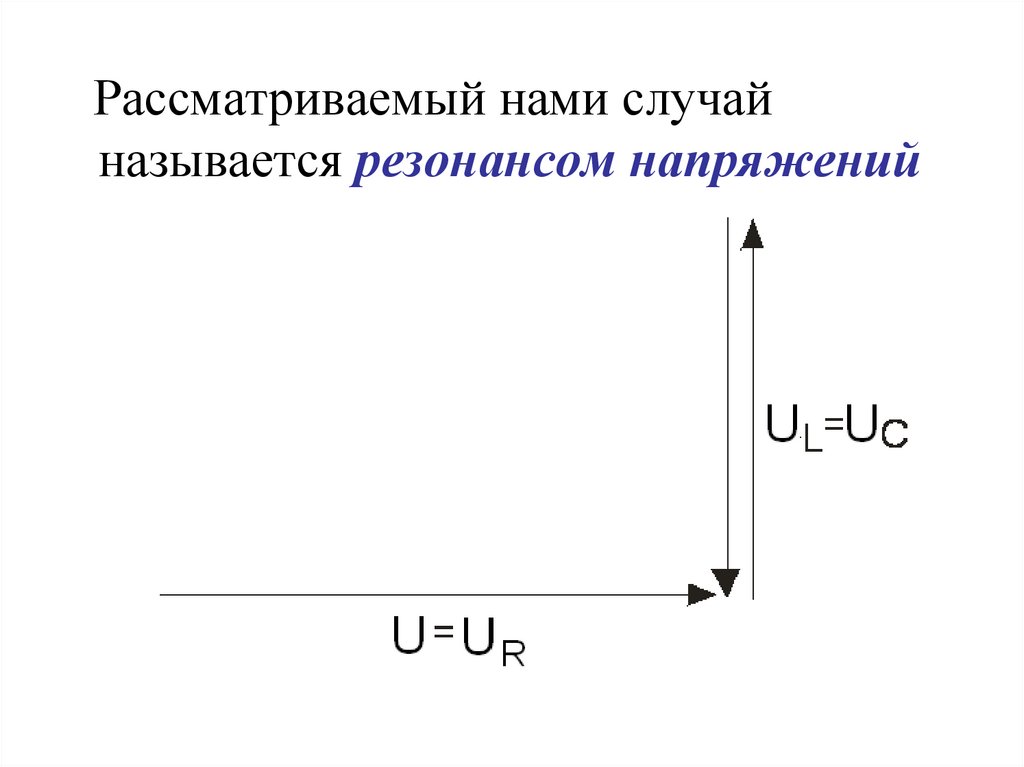
29.

Рассматриваемый нами случай
называется резонансом напряжений

30.

Косинус угла сдвига фаз при таком
режиме становится равным единице, а
угол сдвига фаз – нулю, то есть
R R
cos 1 0
Z R

31.

Режим резонанса напряжений в
электрической цепи нежелателен, так
как напряжения на зажимах
конденсатора и индуктивности могут
значительно превышать напряжение,
приложенное к цепи, и может
возникнуть аварийный режим (сгорят
участки цепи, имеющие малое
сопротивление).

32. Домашнее задание

• Евдокимов Ф.Е. Теоретические
основы электротехники.
Гл. 13,14; § 13.3, 13.5, 14.1-14.2 ; с.
244-248, 256-270.
• Немцов М.В., Немцова М.Л.
Электротехника и электроника.
Гл. 4, § 4.9-4.10, с. 104-111.