Похожие презентации:
Элементы теории множеств
1.
Дискретная математикав программировании
Часть IV
Костюк Ю.Л.
доктор технических наук, профессор
kost@inf.tsu.ru
2.
Элементы теории множествМножество
набор каких-либо объектов – элементов этого множества
Универсальное множество (универсум)
набор всех возможных объектов, их количество – n,
элементы в нём перенумерованы: 1, 2, 3, . . ., n
Другие множества
подмножества универсума
x A - элемент х принадлежит множеству А
y A - элемент y не принадлежит множеству А
B A - множество В является подмножеством множества А
|A|
- количество элементов в множестве А
Ø
- пустое множество
3.
Операции над множествамиПересечение множеств А и В:
C A B
Объединение множеств А и В: C A B
Дополнение множества А:
С=\А
Разность множеств А и В:
С = А \ В= А \ В
Симметрическая разность множеств А и В:
C A B ( A \ B) ( B \ A) ( A \ B) ( B \ A).
Пример:
А = {3, 7, 9}, B = {2, 3, 5, 6, 9}
C A B {3, 9}. C A B {2, 3, 5, 6, 7, 9}.
С = \ А = {1, 2, 4, 5, 6, 8, 10}, С = \ B = {1, 4, 7, 8, 10}
С = А \ В = {7}, С = B \ А = {2, 5, 6}
С = А В = {2, 5, 6, 7}
4.
Множество - битовый векторВ универсуме n элементов,
множество А: биты a1 a2 . . . an,
если ai = 1, то i–й объект принадлежит множеству А, если ai = 0, то нет.
множество B: биты b1 b2 . . . bn, множество C: биты c1 c2 . . . cn.
Пересечение множеств А и В :
для всех i = 1, 2, . . ., n, ci = ai Λ bi.
Объединение множеств А и В :
для всех i = 1, 2, . . ., n, ci = ai V bi.
Дополнение множества А: ci = ¬ai
Разность множеств А и В :
для всех i = 1, 2, . . ., n, ci = ai Λ ¬bi.
Симметрическая разность множеств А и В :
для всех i = 1, 2, . . ., n, ci = ai bi.
Проверка того, что B A : если A B B
то В принадлежит А.
5.
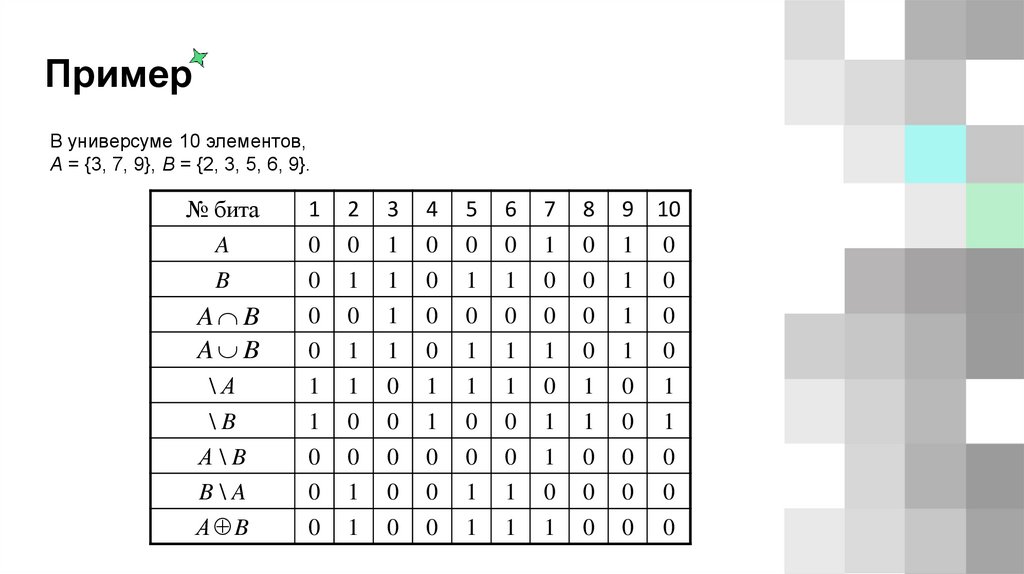
ПримерВ универсуме 10 элементов,
А = {3, 7, 9}, B = {2, 3, 5, 6, 9}.
№ бита
1
2
3
4
5
6
7
8
9 10
A
0
0
1
0
0
0
1
0
1
0
B
0
1
1
0
1
1
0
0
1
0
A B
A B
0
0
1
0
0
0
0
0
1
0
0
1
1
0
1
1
1
0
1
0
\А
1
1
0
1
1
1
0
1
0
1
\B
1
0
0
1
0
0
1
1
0
1
А\B
0
0
0
0
0
0
1
0
0
0
B\A
А B
0
1
0
0
1
1
0
0
0
0
0
1
0
0
1
1
1
0
0
0
6.
ПримерУниверсум – группа студентов
Множество А: кто знает немецкий язык,
Множество В: кто знает английский язык,
Множество С: кто знает французский язык.
A B C : кто знает все три языка,
A B C : кто знает хотя бы один из этих языков,
A B C : кто знает только один из этих языков.
7.
База данных – таблица из строки столбцов (реляционные БД)
Строка таблицы состоит из полей, каждое поле имеет
название, задаёт вид значений (числа, символы)
Вся таблица – множество строк (объектов)
Универсум – всевозможные строки
Пример: таблица успеваемости студентов
Фамилия
Имя
Отчество
История
Информатика
Иванов
Иван
Иванович
5
3
Петров
Пётр
Петрович
4
5
...
...
...
...
...
8.
Действия с таблицейДобавление строк
Удаление строк
Поиск строк по поисковому запросу
Поисковый запрос
логическое выражение над именами полей,
т.е. столбцов, с применением операций сравнения
Пример
история = 5 Λ информатика ≥ 3
Результат: те строки, для которых после подстановки
значений полей в запрос получится «истина»
9.
Библиотечная база данных –множество описаний книг
Описание книги – множество ключевых слов (терминов)
Всё множество терминов – универсум,
k – количество терминов
Описание книги – битовый вектор
Таблица соответствия: термин – номер бита
Всего возможно 2k различных битовых векторов,
т.е. различных описаний книг
10.
Библиотечная база данных –множество описаний книг
Поисковый запрос
логическое выражение над терминами
Результат поиска
книги, у которых «истина» после подстановки бит описания в запрос
Пример запроса
кулинарные рецепты Λ (супы V мясные блюда)
11.
Задания для самостоятельнойработы
В универсуме 6 элементов.
Заданы два множества: А = {3, 4, 6}, B = {2, 3, 5}
1 Записать в виде битового вектора A B
2 Записать в виде битового вектора A B
3 Записать в виде битового вектора A \ B
4 Записать в виде битового вектора B \ A
5 Записать в виде битового вектора A B
6 Записать в виде битового вектора \ A
12.
Задания для самостоятельнойработы
В библиотечной базе данных используются,
в частности, следующие термины:
1 – язык программирования; 2 – файлы; 3 – функции;
4 – Паскаль; 5 – Питон; 6 – С++; 7 – Оберон; 8 – Лисп.
Номер термина – это номер бита в описании книг.
Заданы два множества: А = {3, 4, 6}, B = {2, 3, 5}
Номер термина
Номер книги
1
2
3
4
5
6
7
8
1
1
1
1
1
0
0
0
0
2
1
0
0
0
1
0
0
0
3
1
1
1
0
0
1
0
0
4
1
1
1
0
0
0
1
0
5
1
0
1
0
0
0
0
1
через 1 пробел номера книг, соответствующих запросу:
7 Записать
язык программирования Λ функции Λ ¬ Оберон.
Записать через 1 пробел номера книг, соответствующих запросу:
8 файлы Λ функции Λ ¬ Питон Λ (Паскаль V С++).












 Математика
Математика








