Правила разработки элективного курса

1. Правила разработки элективного курса

2. Элективный курс по физике 9 класс Методы решения физических задач

3. Алгоритмы решения задач по механике

I. Содержание
1.1 Пояснительная записка
1.2 Тематическое планирование
II. Требования к элективному курсу
III. Литература

4. Требования к элективному курсу по физике

На каком содержательном
материале
Чем содержание курса будет
качественно отличаться от
базового курса…
Алгоритмы решения задач по механике
Мало времени уделяется для решения
задач, поэтому программа позволит
глубже рассмотреть физические
закономерности, научить разбираться в
них и применять их к анализу
физических явлений, к практическим
вопросам.
Дидактический материал В.И. Гутман,
В.Н. Мощанский «Алгоритмы решения
Какими учебными и
вспомогательными материалами задач по механике в средней школе»,
Г.Н. Степанова «Сборник задач по
обеспечен
физике»

5.

Какие виды
деятельности
возможны…
Возможны:
Собственная деятельность по
созданию положительной мотивации
учения
Восприятие новых знаний и умений
Познание закономерностей и
законов понимание причинноследственных связей
Практическая деятельность по
самостоятельному решению
возникающих проблем
Самоконтроль, самодиагностика
достижений

6.

Какие виды работ
могут выполнить
учащиеся
Написание контрольных работ
Создание презентации с алгоритмами решения
задач
Создание банка задач
Какова доля
самостоятельности
ученика
Учащиеся могут выбрать
Вид отчетных работ из предложенного перечня,
Литературу, по которой они будут готовить
собственные работы.
Каковы критерии
успешности
(конкретные
требования к
оформлению см.
дополнительно)
Ученик получает зачет (оценка не ниже «4») при
условии:
Выполнения не менее 3 обязательных работ,
представленных в установленный в предложенной
учителем форме с соблюдением стандартных
требований к их оформлению.
Дополнительные баллы выставляются (за любое из
названных дополнительных условий
:Инициативно качественно выполнение задание
помимо обязательных;
Использование Интернет-технологии
Инициативную публичную презентацию своей
работы в школе или за ее пределами (конкурс, смотр,

7.

Каким образом в процессе
работы будет фиксироваться
динамика интереса
Какова форма итоговой
отчетности
Анкетирование на первом и последнем
занятии.
Собеседование в процессе работы после
выполнения каждого вида обязательных
работ (т.е. не менее 3 раза за цикл
обучения)
Итоговый тренинг.
Итоговая конференция с сопутствующей
выставкой работ учащихся.

8. Цели курса

Создание условий для формирования и развития у обучающихся:
Умения решать задачи
Умения самостоятельно приобретать и применять знания
Развитие творческих способностей
В процессе обучения учащиеся приобретают следующие конкретные
умения:
Анализировать
Правильно выбрать алгоритм решения задач
Критически оценивать возможность предложенного варианта решения
задач и своих действий.
Правильно оформлять задачу.
Перечисленные умения формируются на основе следующих знаний:
Теоретического материала базовой программы
Математического аппарата (уравнения в векторном виде,
тригонометрические функции, работа со степенями и т.д.)
умения действовать по образцу (алгоритмическая грамотность);
общеучебных умений (правильно читать текст, находить ответ на вопрос,
составлять план, находить ключевую мысль, оформлять структуру
содержания в виде модели /выделять компоненты и связи/,
составлять таблицы, работать со схематической, графической и
символической наглядностью и др.};
Дополнительного материала предложенного учителем.
информационной грамотности;

9. В процессе изучения курса учащиеся знакомятся с видами задач:

В процессе изучения курса учащиеся знакомятся с видами
:
задач
Задачи можно классифицировать по различным
признакам:
По содержанию: абстрактные и конкретные, с
производственным и историческим содержанием,
занимательные.
По дидактической цели: тренировочные,
контрольные, творческие.
По способу задания условия: текстовые,
графические, задачи – рисунки, задачи-опыты.
По степени трудности: простые (содержат одно –
два действия), сложные, комбинированные.
По характеру и методу исследования:
количественные, качественные,
экспериментальные.

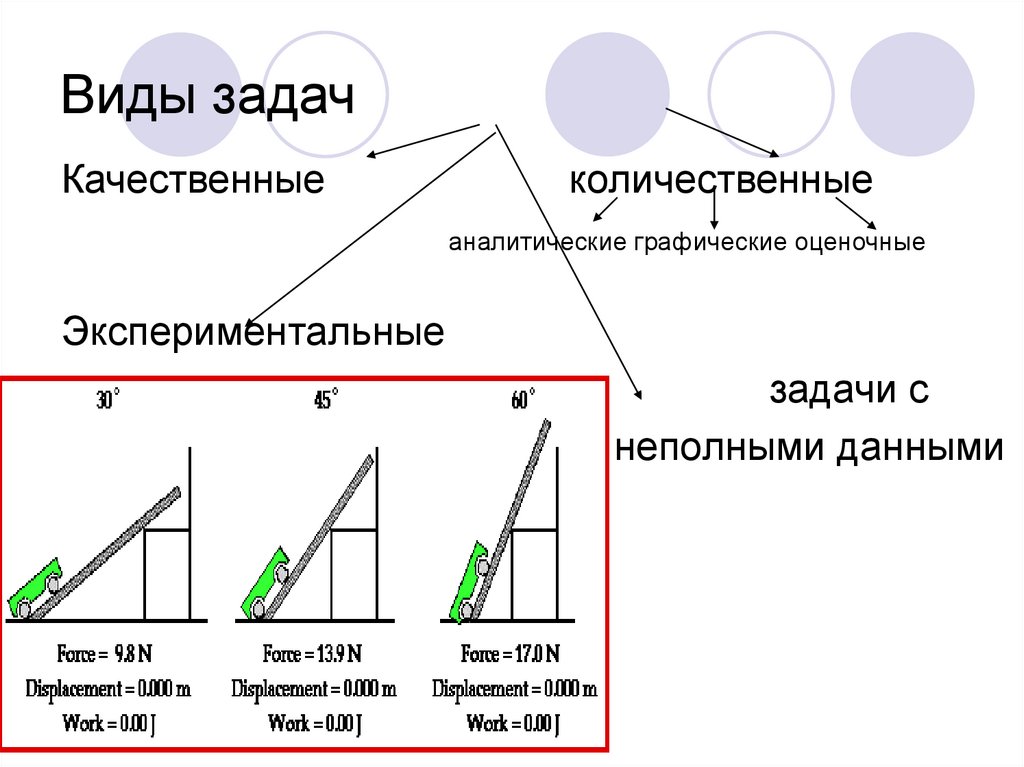
10. Виды задач

Качественные
количественные
аналитические графические оценочные
Экспериментальные
задачи с
неполными данными

11. Охарактеризуем некоторые виды задач

Качественные задачи
не требуют математических расчетов и по типу условия делятся на словесные, графические и
экспериментальные. Основная цель качественных задач — научить:
различать физические явления и процессы в природе и технике;
объяснять физические явления и процессы на основе имеющихся теоретических знаний.
Использование таких задач способствует развитию речи учащихся, формированию у них умения
ясно, логически и точно излагать мысли, оживляет изложение материала, активизирует
внимание учащихся.
Количественные задачи
для решения требуют проведения математических расчетов. По типу решения их принято
подразделять на:
аналитические (решаются посредством использования одного или нескольких необходимых
уравнений);
графические (решаются посредством построения графика); позволяют наглядно наиболее ярко и
доходчиво выражать функциональные зависимости между величинами, характеризующими
процессы, протекающие в окружающей нас природе и технике.
оценочные (для их решения необходимо сформулировать простую физическую модель
рассматриваемого явления, подобрать разумные значения необходимых физических величин и
получить примерный числовой результат, например: «Оценить, с какой скоростью может
бежать по Луне космонавт в легком, удобном скафандре»)',
экспериментальные – задачи, данные для решения которых получают из опыта при
демонстрации, или же при выполнении самостоятельного эксперимента. При решении этих
задач учащиеся проявляют особую активность и самостоятельность. Преимущество
экспериментальных задач перед текстовыми заключается в том, что первые не могут быть
решены формально, без достаточного осмысления физического процесса.
Задачи с неполными данными чаще всего встречаются в жизни, когда недостающие сведения
приходится добывать из таблиц, справочников, либо путем измерений. Решение задач этого
типа способствует формированию навыков самостоятельной работы учащихся со справочной
литературой.

12. Методика обучения учащихся решению физических задач.

При решении задач используют различные методы:
Аналитический, который заключается в
расчленении сложной задачи на ряд простых
(анализ), при этом решение начинается с
отыскания закономерности, которая дает
непосредственный ответ на вопрос задачи.
Окончательная расчетная форма получается путем
синтеза ряда частных закономерностей.
Синтетический, когда решение задачи начинается
не с искомой величины, а с величин, которые могут
быть найдены непосредственно из условия задачи.
Решение развертывается постепенно, пока в
последнюю формулу не войдет искомая величина.
При таком подходе решение задачи опять же надо
начинать с анализа явления.

13. Структура процесса решения задачи:

Ознакомление с условием задачи.
Составление плана решения задачи.
Осуществление решения.
Проверка правильности решения задачи

14.

Исходя из приведенного выше, можно выделить
следующие этапы формирования у учащихся
умения решать задачи по физике:
1.Анализ. Условие задачи представляет собой код. На первом
этапе происходит перекодирование информации — краткая
запись условия задачи, рисунки, чертежи.
2.Выявление структуры процесса решения задачи. Основное
внимание следует уделить овладению учащимися общими
операциями по решению физической задачи любого типа.
Перечислим указанные операции:
выбор рациональных способов решения задачи;
выполнение приближенных вычислений;
выполнение действий с именованными величинами;
преобразования единиц величин;
применение различных способов проверки;
анализ результатов.
Операции отрабатываются в процессе решения конкретных
задач.

15.

3.Усвоение общей структуры решения класса задач по
конкретной теме, на применение конкретных физических
законов. Усвоенные ранее операции выстраиваются в
стройную систему, которую можно рассматривать как
предписание алгоритмического типа для решения задач
по определенным темам.
4.Предписание алгоритмического типа для решения задач
определенного вида (качественные,
количественные, экспериментальные и др.) по
конкретным темам и на конкретные законы обобщаются в
общие предписания алгоритмического типа для решения
задач этою вида.
5.Происходит дальнейшее обобщение предписаний
алгоритмического типа, при этом вырабатывается общее
предписание алгоритмического типа для решения любой
физической задачи.

16. Учащимся можно предложить памятку по решению физических задач:

Учащимся можно предложить памятку по решению физических задач
:
1. Этап
Изучите условия, сделайте краткую запись данных при помощи принятых
обозначений. Изучить условие - значит постараться представить себе
явление или процесс, который описан в содержании задачи.
2. Этап
Подробно всесторонне рассмотрите физические явления и процессы, о
которых идет речь в задаче. Выявите и рассмотрите начальное и
конечное состояние процесса и параметры, их характеризующие. Это
поможет вам уточнить условие, поставить соответствующие индексы к
буквенным обозначениям.
3. Этап
Найти (извлечь из памяти) ту закономерность - закон, формулу, правило которая описывает данное явление или процесс.
этап
4. Сделайте проверку, соответствует ли число полученных уравнений числу
неизвестных; все ли величины, входящие в расчетную формулу,
определены. Проверьте соответствие размерности искомой величины по
расчетной формуле.
5. Этап
Вычислите значение искомой величины, дайте анализ полученною ответа.

17. Содержание программы элективного курса

1. Введение – 1 час
-Физические задачи и их роль в преподавании физики
-Виды физических задач
2. Об использовании алгоритмического подхода к решению физических
задач – 1 час
3. Алгоритм решения задач по кинематике материальной точки – 5 часа
4. Тренинг. Тест №1.
5. Алгоритм решения задач по динамике материальной точки – 5 часа
6. Тренинг. Тест № 2.
7. Алгоритм решения задач по статике – 5 часа
8. Тренинг. Тест № 3.
9. Алгоритм решения задач на закон сохранения импульса – 5 часа
10. Тренинг. Тест № 4.
11. Алгоритм решения задач на закон сохранения механической энергии –
5 часа
12. Тренинг. Тест №5.
13. Конференция - 2 часа

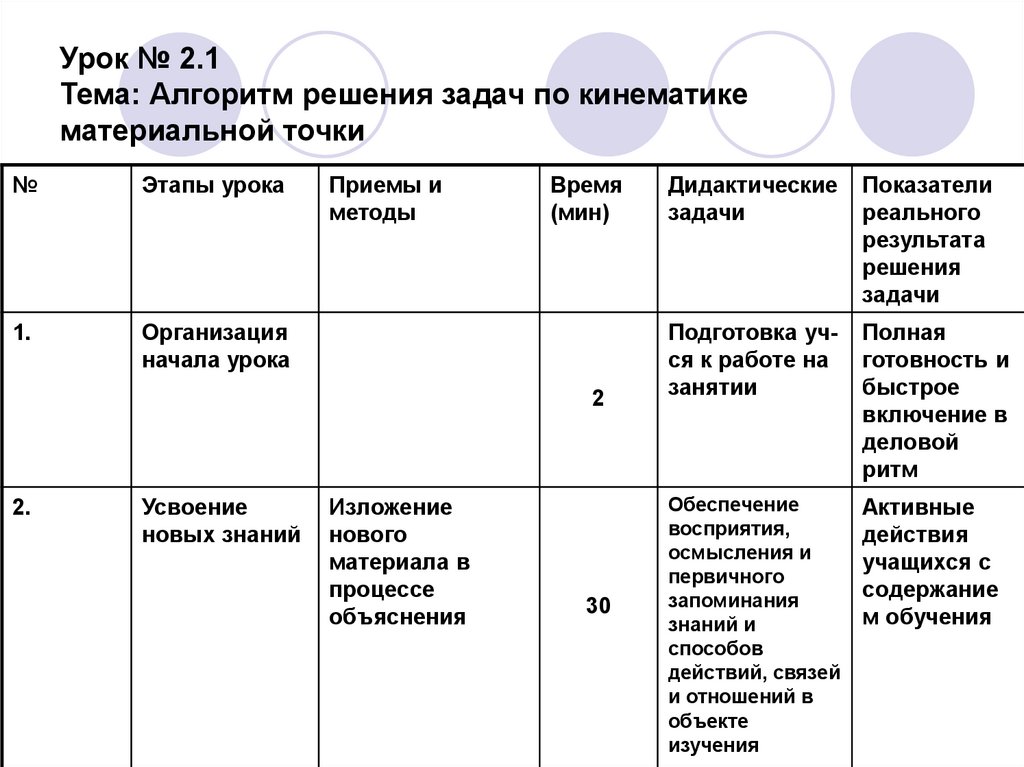
18. Урок № 2.1 Тема: Алгоритм решения задач по кинематике материальной точки

№
Этапы урока
1.
Организация
начала урока
Приемы и
методы
Время
(мин)
2
2.
Усвоение
новых знаний
Изложение
нового
материала в
процессе
объяснения
30
Дидактические
задачи
Показатели
реального
результата
решения
задачи
Подготовка учся к работе на
занятии
Полная
готовность и
быстрое
включение в
деловой
ритм
Обеспечение
восприятия,
осмысления и
первичного
запоминания
знаний и
способов
действий, связей
и отношений в
объекте
изучения
Активные
действия
учащихся с
содержание
м обучения

19.

3.
Подведение итогов
занятий
Краткое
повторение
нового
материала
8.
Дать анализ и
оценку
успешности
достижения
цели и
наметить
перспективу
последующей
работы
Получение
уч-ся
информации
о реальных
результатах
учения

20.

Для овладения методом решения кинематических
задач учащиеся должны усвоить следующие
вопросы: понятия — система отсчета,
скорость, ускорение; уравнения,
определяющие зависимость координат и
скорости от времени в равномерном и
равноускоренном движениях, закон сложения
скоростей Галилея, идею о том, что всякое
движение можно разложить на два (в общем
случае — на три) простых движения вдоль
осей координат; идею о том, что любое
тело, какую бы скорость оно ни имело, будет
двигаться под действием притяжения к
Земле с ускорением, равным g, направленным
вертикально вниз (при отсутствии
сопротивления среды).

21.

Задача 1. Два автомобиля движутся прямолинейно в одну
сторону с постоянными скоростями v1 и v2 (причем v1>v2),
и в некоторый момент времени расстояние между ними
равно s. Через сколько времени и в каком месте первый
автомобиль догонит второй?
Решение:
Используя общий план решения любой физической задачи,
после изучения и записи условия, выполнения чертежа
(рис. 1), выбираем систему отсчета, т. е. тело отсчета
(Земля), начало системы координат (точка А),
положительное направление оси (направление движения) и
момент времени, принимаемый за начальный (момент,
когда автомобили находились на расстоянии s).
Анализируем описанные в тексте физические процессы.

22.

Обе материальные точки движутся равномерно и прямолинейно,
следовательно, их движения описываются уравнениями
х1 = х01 + v1х t, х2 = х02 + v2х t,
Чтобы решить вопрос о последующем состоянии точек, надо знать их
начальные состояния, начальные условия, т. е. координаты и скорости
в момент времени, принимаемый за начальный. Начальная скорость
обычно обозначается v0. Так как автомобили движутся равномерно,
то их начальная скорость совпадает со скоростями в любые
последующие моменты и потому: х01 = 0,
v01х = v1; х02 = s, v02х = v2.
С учетом этого уравнения примут вид: х1 = v1t, х2 = s + v2 t.
4.
Эти уравнения справедливы для любого момента времени, для
любой точки траектории (здесь t — переменная величина, которая
может принимать любые значения). Следовательно, они
справедливы и для интересующего нас момента, когда первый
автомобиль догонит второй в точке С. Обозначим этот момент
времени . Тот факт, что один автомобиль догнал другой, означает, что в
момент t 1= t они находились в одной и той же точке пространства, т. е.
х1=x2 = хс. Тем самым мы выявили в тексте задачи дополнительные
условия, выразили их на математическом языке, и теперь можно
написать уравнения для данного момента времени, т. е.
для движения в точке С: хс = v1t,
хс = s + v2 t
Отсюда
t= s/ (v1 – v2), хс = v1s / (v1 – v2).
После решения данной задачи выделяются основные этапы, «шаги»
решения, затем решается другая задача по тем же этапам.

23.

Задача 2. Два автомобиля движутся навстречу друг
другу с постоянными скоростями v1 и v2. Первый
автомобиль проходит пункт А на промежуток
времени ∆t раньше, чем второй проходит пункт В.
Определить, когда и где произойдет их встреча,
если расстояние между А и В равно s.
Решение
1. Выберем систему отсчета (рис. 2). Систему
координат свяжем с Землей, начало отсчета выберем в точке А за положительное направление оси
Ох примем направление от А к В, за начальный
момент времени t = 0 примем момент, когда первый
автомобиль проходил точку А.
2. Из условия ясно, что оба автомобиля двигались
равномерно, следовательно, можно написать для
каждого кинематические уравнения равномерного
движения
х1 = х01 + v1х t1 , х2 = х02 + v2х t2.

24.

3.Для определения того, где будет
находиться материальная точка в
последующие моменты времени, надо знать
начальные условия (а если движение
равноускоренное, то и ускорение точки).
Определим начальные условия: х01 = 0,
v01х = v1 =const; х02 = s, v02х = -v2 = const.
С учетом этого уравнения приобретут вид:
х1 = v1t1,
х2 = s - v2 (t1 - t2)

25.

4.Эти уравнения справедливы для любого момента
времени, для любой точки траектории, следовательно, они
справедливы и для интересующего нас момента —
момента встречи. В условии задачи явно заданы четыре
величины (s, v1, v2, ∆ t ), но, кроме этого, в тексте
содержится дополнительное условие, состоящее в том, что
автомобили встретились в некоторый момент времени в
некоторой точке траектории. Эти дополнительные условия
надо выразить на математическом языке и ввести в
уравнения движения. Обозначим время, прошедшее до
момента встречи, через т, а координату точки встречи (точки
С) — xc. Слова условия о том, что автомобили
встретились, означают, что в момент t1 = координаты
автомобилей одинаковы, т. е. для точки С имеем:
t1 = , х1 = х2 = хс . Напишем уравнения движения для
момента , для точки С:
х1 = v1 ,
х2 = s - v2 ( t - ∆t).
Решение этой системы уравнений дает: = s + v2∆t/ (v1 + v2),
хс = [s + v2∆t / (v1 + v2)]*v1.

26. алгоритм решения кинематических задач:

Сравнение решения обеих задач позволяет выявить общность в
последовательности действий и сформулировать следующий
алгоритм решения кинематических задач:
выбрать систему отсчета (это предполагает выбор тела
отсчета, начала системы координат, положительного
направления осей, момента времени, принимаемого за начальный);
определить вид движения вдоль каждой из осей и написать
кинематические уравнения движения вдоль каждой оси — уравнения
для координаты и для скорости (если тел несколько, уравнения
пишутся для каждого тела);
определить начальные условия (координаты и проекции скорости в
начальный момент времени), а также проекции ускорения на оси и
подставить эти величины в уравнения движения;
определить дополнительные условия, т. е. координаты или
скорости для каких-либо моментов времени (для каких-либо точек
траектории), и написать кинематические уравнения движения для
выбранных моментов времени (т. е. подставить эти значения координат и скорости в уравнения движения);
полученную систему уравнений решить относительно искомых
величин.

27.

Формулируя этот алгоритм, надо объяснить
учащимся, что в задачах 1 и 2, на решение которых
опиралось его обоснование, материальные точки
двигались равномерно вдоль одной оси; однако в
дальнейшем будут изучаться другие виды
движения, описываемые другими кинематическими
уравнениями, и чтобы знать, какое уравнение
использовать, надо прежде всего установить, каков
вид движения материальной точки вдоль оси. При
этом иногда придется рассматривать движение
вдоль не одной, а двух осей, и надо будет
выяснять вид движения вдоль каждой оси.