Похожие презентации:
О курсе общей физики
1. О курсе общей физики
Сегодня: воскресенье, 29 января 2017 г.Гирякова Ю.Л.
О курсе общей физики
План работы:
4 Лекции
2 Практики
4 Лабораторные работы
Экзамен
29.01.2017
Допуск к экзамену:
Сдать 2 ИДЗ
Выполнить 2 лб
Сдать конспект
1
2.
Список литературы1. Т.И. Трофимова. Курс физики. –М.: Высшая
школа, 2007. – 658 с.
2. С.И. Кузнецов. Физика, часть 1. Механика и
молекулярная физика
29.01.2017
2
3.
Общие положенияФизика, которая развивалась в течение
трех
столетий
достигла
своей
кульминации во второй половине XIX в.
созданием электромагнитной теории
света, называется
классической физикой.
Рассматривает движение при v<<c (с-это
скорость света в вакууме). Размеры
пространства много больше длины волны
де Бройля.
29.01.2017
3
4.
На рубеже XIX и XX в.в. новыеэксперименты и новые идеи в физике
стали указывать на то, что некоторые
аспекты
классической
физики
неприменимы к
миру атома, а так же к объектам,
движущимся
с
очень
большой
скоростью. Следствием всего этого
явилась очередная великая революция
в физике. Родилась
современная физика.
29.01.2017
4
5. Общефизические положения
Объединительные идеи в физикеДо Ньютона механика делилась на земную и
небесную. Ньютон объединил обе механики
в одну, которая до сих пор называется
механикой Ньютона или классической
механикой. Уравнение движения небесных
и земных тел имеет одинаковый вид и
смысл.
29.01.2017
5
6.
Впоследствии объединительные идеисыграли выдающуюся роль в физике
и во всем естествознании. Были
объединены механические и
тепловые явления; электричество и
магнетизм (поля электрические и
магнитные - Максвелл);
электромагнетизм и оптика –
электромагнитные волны; оптические
и тепловые явления – квантовая
оптика,
29.01.2017
6
7.
гравитация и ускорение (силы инерции итяготения), частица и волна –
корпускулярные свойства волн и волновые
свойства частиц. С помощью теории
относительности Эйнштейна объединены
электрические и магнитные поля (новый
уровень объединения). Конечная цель
всех объединений – создание единой
теории всего и вся как бы «в одном
уравнении».
Самое выдающееся открытие – твердотельная
электроника (компьютеры) и лазеры - это коллективное
мнение ныне живущих лауреатов Нобелевской премии.
29.01.2017
7
8.
Физика изучает1. Физические объекты: атом, ядро, частицы,
молекулы, плазму, частицы и элементарные
частицы, твердое тело, фотоны, кварки и т.д.
Отсюда деление на: физика атомов и
молекул, физика ядра, физика
элементарных частиц, физика твердого
тела.
29.01.2017
8
9.
Физика изучает2. Физические процессы (как форму
движения материи) – отсюда названия
разделов: механика (механическое
движение, термодинамика (тепловое
движение), электродинамика
(электромагнитные явления) и т.д.
29.01.2017
9
10.
Физика наука экспериментальная.Это обозначает, что критерием истины
является эксперимент.
Объем физических знаний неограничен.
Это означает, что на Земле давно нет
такого человека, который бы знал в
физике ВСЁ.
Язык физики – математика.
29.01.2017
10
11. Роль моделей в физике
В механике, например, используют 3 модели материальная точка, абсолютно твердоетело (атт), модель сплошной среды.
Их роль:
1. Основная. 2. Вспомогательная. 3. Для
решения задач. 4. Для решения
фундаментальных проблем. 5. Для
формулирования новых гипотез и теорий.
29.01.2017
11
12. Кинематика движения материальной точки.
Кинематика раздел механики, в которомизучаются геометрические свойства движения
тел без учета их массы и действующих на них
сил. Изучаем кинематику поступательного и
вращательного движения.
29.01.2017
12
13.
Поступательное движение – это движение,при котором любая прямая, жестко связанная
с движущимся телом, остается параллельной
своему первоначальному положению.
Вращательное движение – это движение,
при котором все точки тела движутся по
окружностям, центры которых лежат на одной
и той же прямой, называемой осью
вращения.
29.01.2017
13
14.
• Тело, относительно которогорассматривается движение,
называют телом отсчета.
Система отсчета – совокупность
системы координат и часов,
связанных с телом отсчета.
29.01.2017
14
15.
В декартовой системе координат,используемой наиболее часто, положение
точки М в данный момент времени по
отношению к этой системе характеризуется
тремя координатами X, Y, Z или радиусом –
вектором , проведенным из начала системы
координат в данную точку (рис.1).
29.01.2017
15
16.
Mk
j
i
Рис. 1.
Частица массой М
Радиус-вектор
следит за частицей М
и поворачивается в
пространстве,
изменяя свой длину
по величине и
направлению
(ii)=1; (jj)=1; (kk)=1; (ij)=0; (ik)=0; (jk)=0
29.01.2017
16
17.
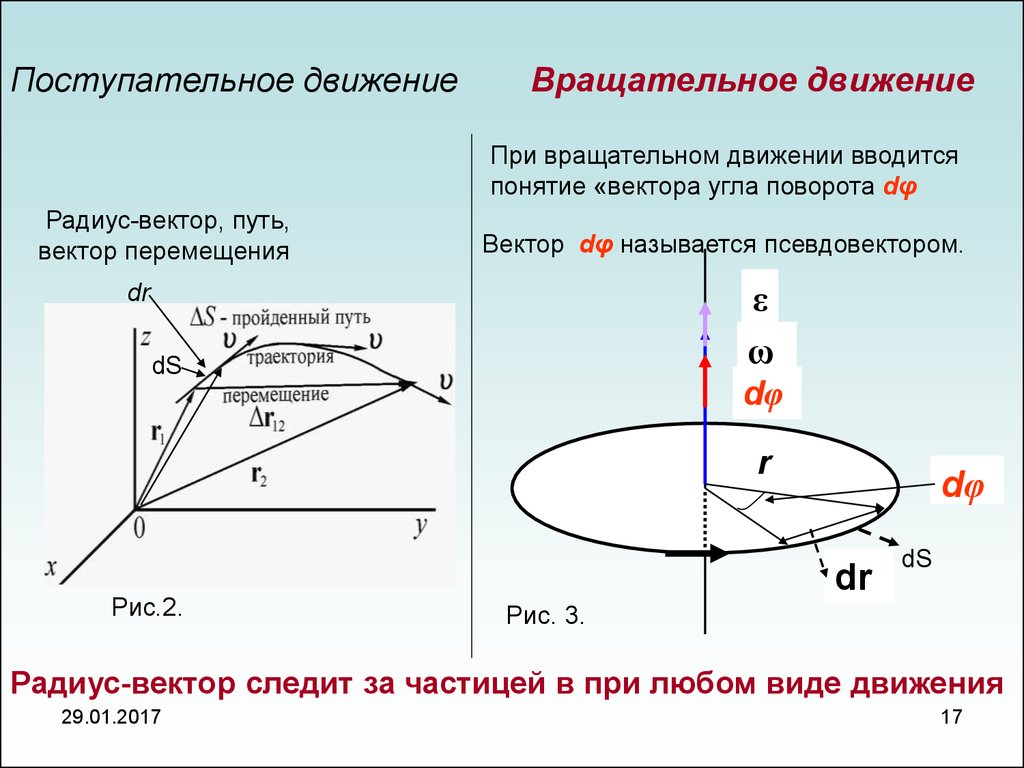
Поступательное движениеВращательное движение
При вращательном движении вводится
понятие «вектора угла поворота dφ
Радиус-вектор, путь,
вектор перемещения
Вектор dφ называется псевдовектором.
ε
ω
dr
dS
dφ
r
Рис.2.
dφ
dr
dS
Рис. 3.
Радиус-вектор следит за частицей в при любом виде движения
29.01.2017
17
18.
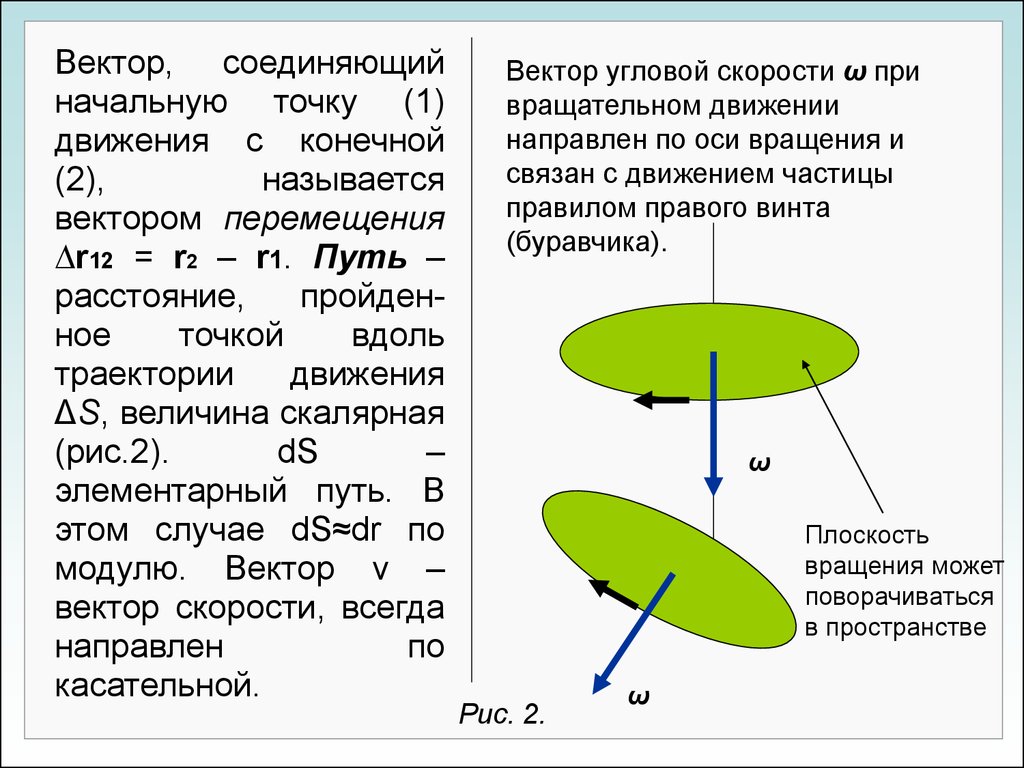
Вектор, соединяющийначальную точку (1)
движения с конечной
(2),
называется
вектором перемещения
r12 = r2 – r1. Путь –
расстояние,
пройденное
точкой
вдоль
траектории
движения
ΔS, величина скалярная
(рис.2).
dS
–
элементарный путь. В
этом случае dS≈dr по
модулю. Вектор v –
вектор скорости, всегда
направлен
по
касательной.
29.01.2017
Вектор угловой скорости ω при
вращательном движении
направлен по оси вращения и
связан с движением частицы
правилом правого винта
(буравчика).
ω
Плоскость
вращения может
поворачиваться
в пространстве
Рис. 2.
ω
18
19.
При движении материальной точки ее координатыс течением времени изменяются. В общем случае
ее движение определяется скалярными
уравнениями
X=X(t), Y=Y(t), Z=Z(t)
(1)
эквивалентными векторному уравнению
(2)
r r(t) x(t) i + y(t) j + z(t) k
где – x, y, z – проекции радиуса – вектора на оси
координат, а i , j , k – единичные векторы,
направленные по соответствующим осям.
Уравнения (1) и соответственно (2) называются
кинематическими уравнениями движения материальной
точки.
29.01.2017
19
20. Скорость при поступательном движении
При делении перемещения r на t получаем векторскорости:
r
v = lim
(определение скорости).
t 0 t
V=
dy t
dr
dx t
dz t
i
j
k
i v x jv y k vz
dt
dt
dt
dt
29.01.2017
20
21. Ускорение при поступательном движении
При делении вектора v на tполучаем вектор ускорения a:
v
a lim
t 0 t
2
2
2
V(t)
ΔV
V(t+Δt)
2
d r dv d x d y d z
a 2 i 2 j 2 k 2 i a x j a y k az
dt
dt
dt
dt
dt
Т.е. нужно два раза продифференцировать радиусвектор r или один раз вектор скорости v
29.01.2017
21
22. Скорость и ускорение при вращательном движении
По аналогии с линейной скоростью и ускорениемвводятся угловая скорость и угловое ускорение.
Величина угловой скорости точки равна углу dφ
поворота радиус-вектора точки в единицу времени
d рад
,
dt с
dr
ω
Вектор угловой скорости направлен по оси
вращения, по направлению вектора dφ.
dr= dφr
Векторы dr, dφ, r связаны как стороны треугольника
29.01.2017
22
23.
Величина =d d
2 (рад/с2) называется угловым
dt dt
2
ускорением и характеризует изменение угловой
скорости в единицу времени.
29.01.2017
23
24.
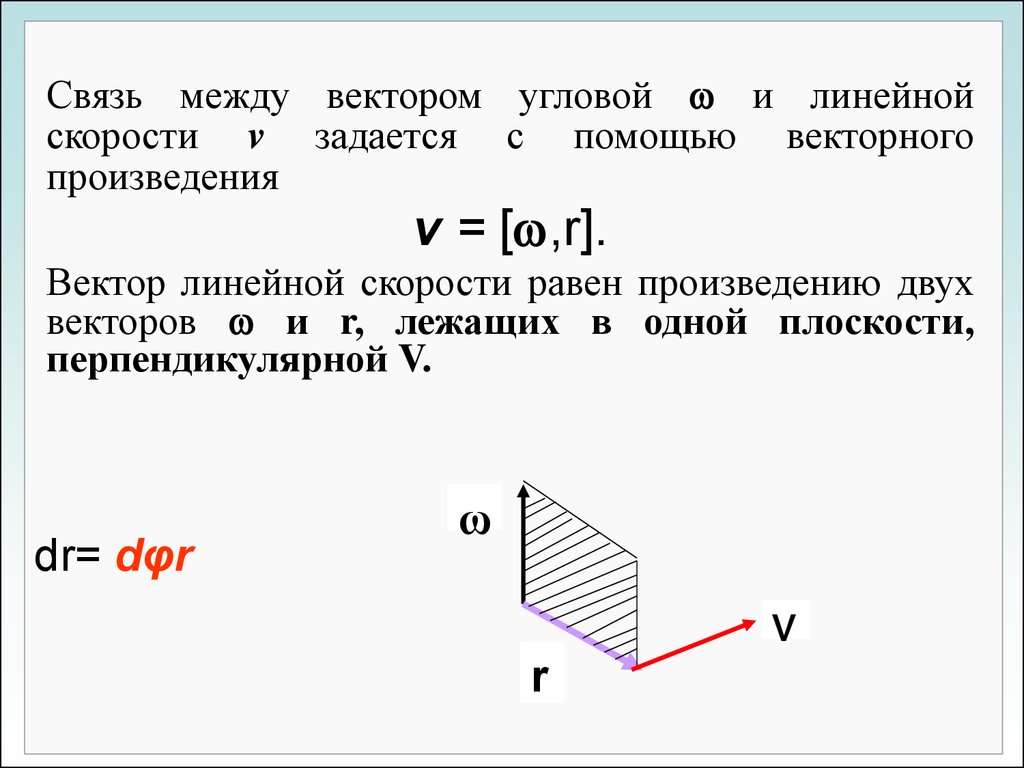
Связь между вектором угловой и линейнойскорости v задается с помощью векторного
произведения
v = [ ,r].
Вектор линейной скорости равен произведению двух
векторов и r, лежащих в одной плоскости,
перпендикулярной V.
dr= dφr
ω
V
r
29.01.2017
24
25.
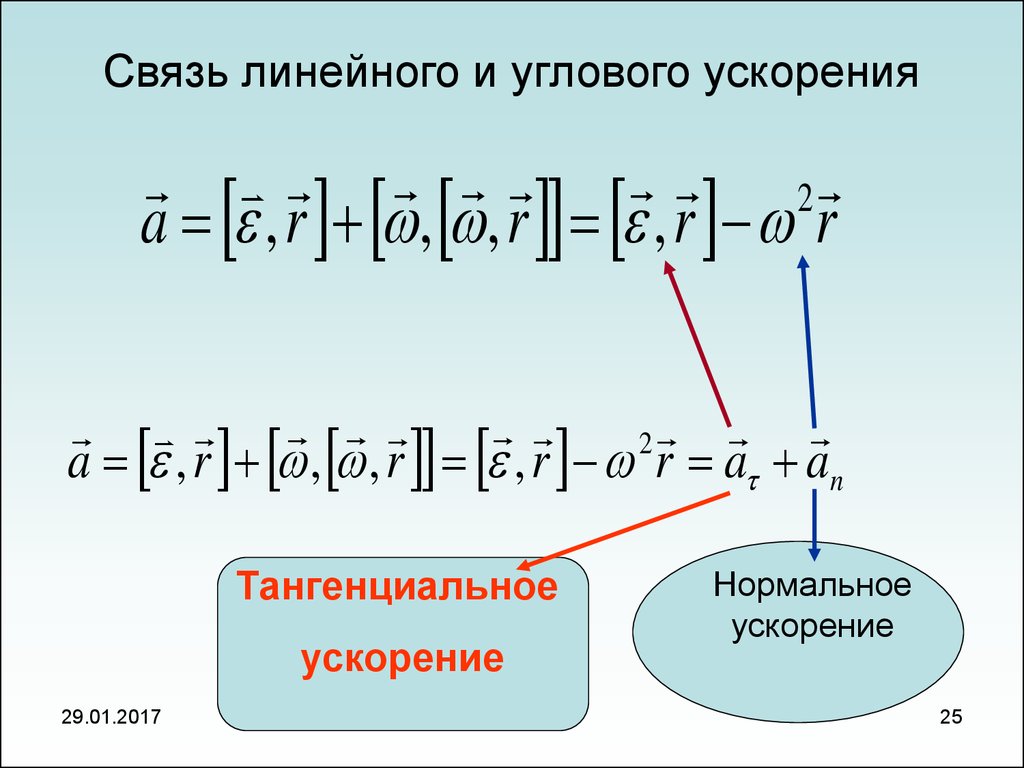
Связь линейного и углового ускорения2
a , r , , r , r r
2
a , r , , r , r r a an
Тангенциальное
ускорение
29.01.2017
Нормальное
ускорение
25
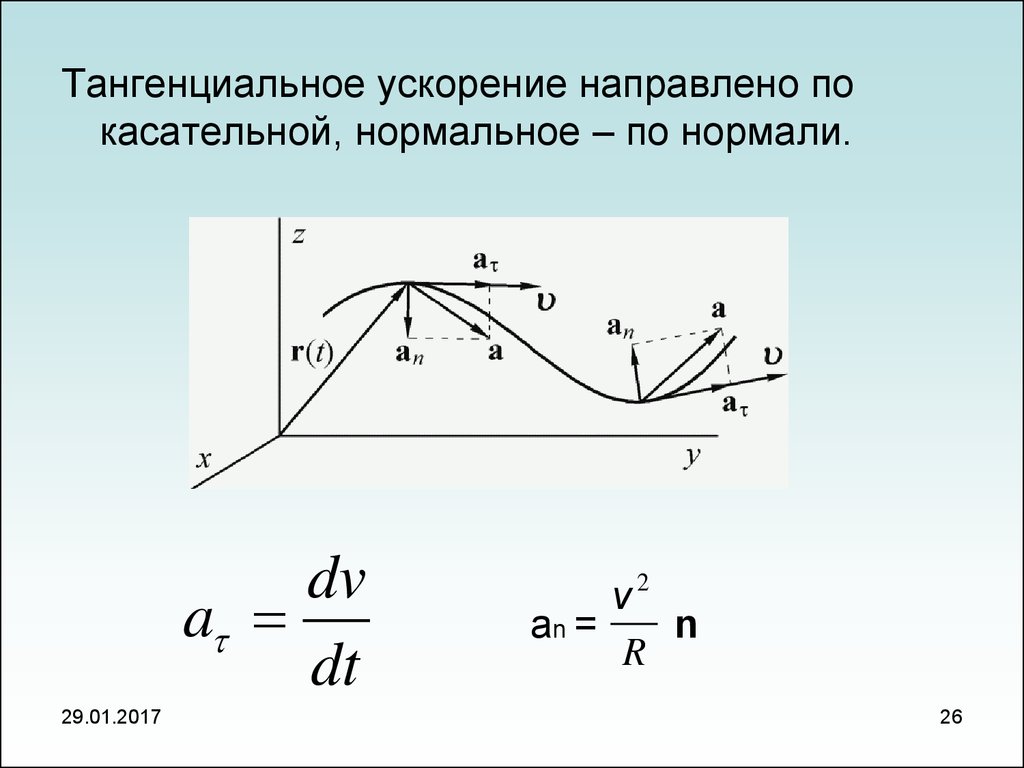
26.
Тангенциальное ускорение направлено покасательной, нормальное – по нормали.
a
dv
dt
aτ
dv
a
dt
29.01.2017
v2
an =
n
R
26
27.
Обратная задача кинематикиЕсли выражение dr =vdt или dS= Vdt
проинтегрировать по времени в пределах от t
до t+∆t, то найдем радиус-вектор или длину
пути пройденного точкой за время ∆t. Такая
процедура называется решением обратной
задачи кинематики, т.е. нахождение пути по
скорости и ускорению.
t2
t t
S
dt
.
t
29.01.2017
S (t )dt.
t1
27
28.
Сегодня: воскресенье, 29 января 2017 г.Тема: КЛАССИЧЕСКАЯ ДИНАМИКА.
ЗАКОНЫ НЬЮТОНА
Законы
классической
динамики
имеют
огромную область применения от описания
движения микроскопических частиц в модели
идеального газа до поведения гигантских тел
во
Вселенной.
осознание
технических
Открытие,
этих
законов
прогресс
применение
и
определяют
человечества
на
протяжении уже более трех веков.
29.01.2017
28
29.
Первый закон НьютонаСмысл первого закона состоит в том, что
если на тело не действуют внешние силы,
то существует система отсчета, в которой
оно покоится. Такая система отсчета
называется инерциальной.
29.01.2017
29
30.
В инерциальной системе отсчетавсякое свободное движение происходит с
постоянной по величине и направлению
скоростью.
29.01.2017
30
31. Второй закон Ньютона. Основные понятия
Второйзакон
Ньютона
количественно
определяет величину силы. Под силой в механике
понимают всякую причину, изменяющую
состояние движения тела.
Всякое тело оказывает сопротивление при
попытках привести его в движение или изменить
модуль или направление его скорости. Это
свойство тел называется инертностью.
Мера инертности тела называется массой.
29.01.2017
31
32.
Импульс или количество движения материальнойточки является вектор, равный произведению массы
точки на ее скорость:
p = mv.
29.01.2017
32
33.
Для системы из двух (и более) материальных точекимпульс – это векторная сумма
p = p1 + p2 = m1v1 + m2v2.
В инерциальной системе отсчета изменение
импульса p материальной точки со временем
представляется уравнением
p = dp/dt = d(mv)//dt = F(r,V).
Для
медленных
движений,
пропорционален скорости:
mv
29.01.2017
когда
импульс
= F(r,V),
33
34.
Величина F(r,V), равная скорости измененияимпульса во времени, называется вектором силы,
действующей на рассматриваемую материальную
точку.
Таким образом, в инерциальной системе
отсчета производная импульса материальной
точки по времени равна действующей на нее
силе. Это утверждение называется вторым
законом Ньютона, а соответствующие ему
уравнения
–
уравнениями
движения
материальной
точки.
29.01.2017
34
35.
Из первого закона следует важныйфизический принцип: существование
инерциальной системы отсчета!
Смысл первого закона состоит в том,
что если на тело не действуют внешние
силы, то существует система отсчета, в
которой оно покоится. Но если в одной
системе тело покоится, то существует
множество других систем отсчета, в
которых тело движется с постоянной
скоростью.
29.01.2017
35
36. 2 закон Ньютона в обобщенном виде
Записывается следующим образом:N
dp
Fi ( r , v )
dt
i 1
где справа векторная сумма всех
действующих на тело (частицу) сил. Или
dp d (mv ) N
Fi (r , v )
dt
dt
i 1
При этом масса зависит от скорости
m
29.01.2017
m0
v
1
c
2
2
36
37. Виды сил и движений
Сила F(r,V) зависит от скорости ирасстояния между
взаимодействующими телами
(полями).
Сила трения (сопротивления)
n
F kv
29.01.2017
37
38. Сила гравитационная
mmcFграв G 3 r
r
Сила упругости (закон Гука)
F kx
29.01.2017
38
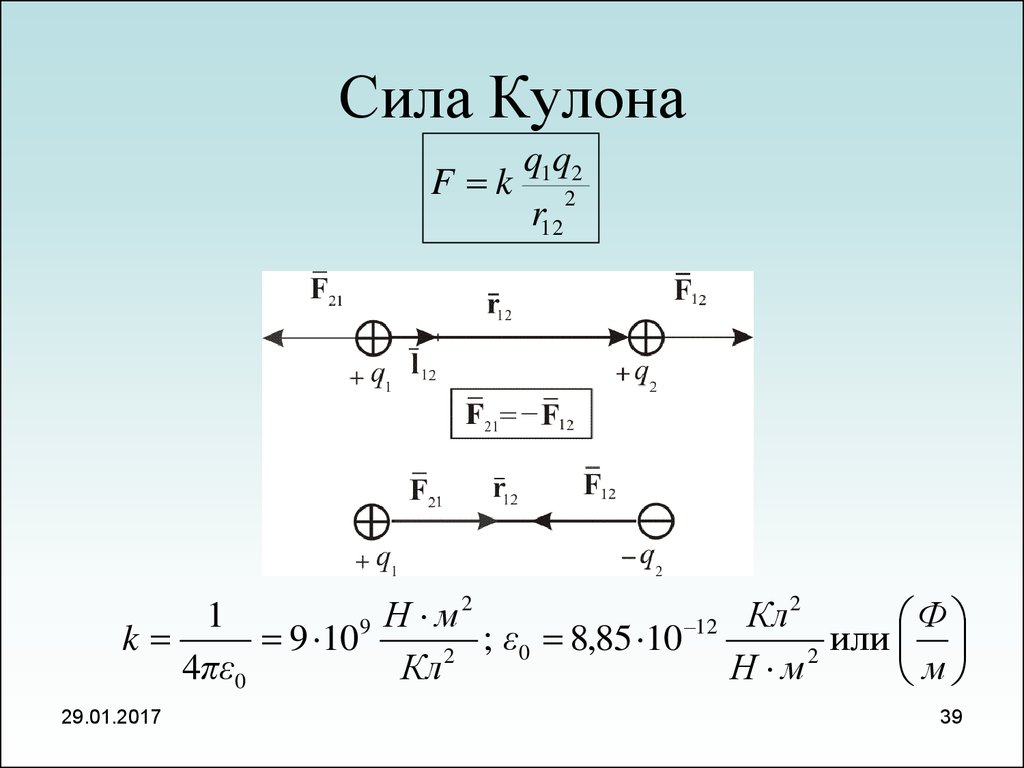
39. Сила Кулона
q1q2F k 2
r12
2
2
1
Н
м
Кл
Ф
9
12
k
9 10
; ε0 8,85 10
или
2
2
4πε0
Кл
Н м
м
29.01.2017
39
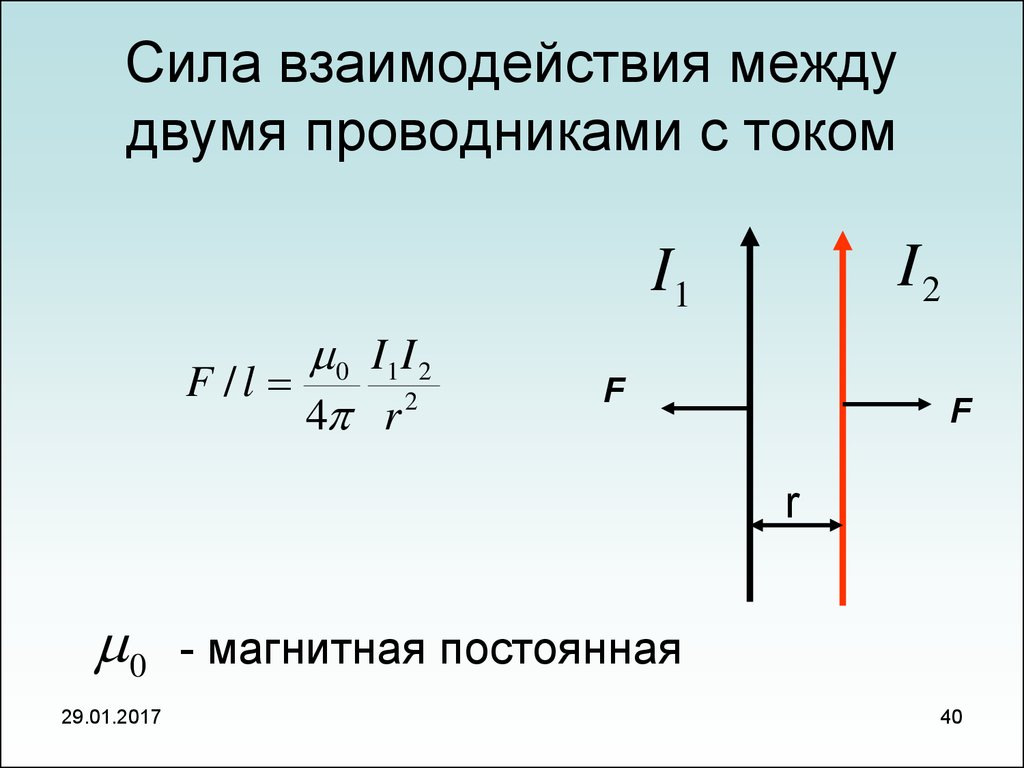
40. Сила взаимодействия между двумя проводниками с током
I2I1
0 I1 I 2
F /l
4 r 2
F
F
r
0
29.01.2017
- магнитная постоянная
40
41.
Поэтому уравнения движения могутиметь разнообразный вид и в
зависимости от этого получают разные
виды движения.
Например в гравитационном или
кулоновском поле уравнение имеет вид:
d r dp
mmc
m 2
G 3 r
dt
dt
r
2
29.01.2017
41
42.
При движении с малыми скоростями (классическаямеханика) v<<c и dm/dv = 0.
При движении со скоростями сравнимыми со
скоростью света dm/dv ≠0.
Замечание. Если положить, что энергия в замкнутой
(консервативной) системе сохраняется, то:
d N
Ei, j U i, j 0
dt i , j 1
i j
Из этого уравнения вытекает 2-ой закон Ньютона.
Этот пример показывает вариативность подходов к
решению физических проблем. Закон сохранения
энергии – следствие однородности времени.
29.01.2017
42
43.
Связь между силой ипотенциальной энергией.
Чтобы найти силу, действующую на частицу в
потенциальном поле необходимо
продифференцировать по координате формулу
для потенциальной энергии и приписать знак
«минус».
d
Fx (U )
dx
29.01.2017
d
Fy (U )
dy
d
Fz (U )
dz
43
44. Например, связь потенциальной энергии и силы тяжести
Потенциальная энергия частицы массой mвблизи поверхности Земли имеет вид U=mgz,
z – координата частицы
z
dU
d (mgz)
F
mg
dz
dz
U=mgz
F=mg
z
Координата направлена вверх по оси z, сила вниз – поэтому знак «минус»
29.01.2017
44
45. Как изменяется характер движения при изменении функции F(r,v)
Если сила постоянная, то имеем ускоренноедвижение, параметры которого определяем,
решая обратную задачу кинематики.
Ускорение a равно F/m или a=dV/dt.
Отсюда dV=(F/m)dt, m = const.
Интегрируя это уравнение, находим скорость,
при последующем интегрировании находим
координаты x,y,z, т.е. траекторию движения
(прямая, парабола и т.д).
29.01.2017
45
46.
Если сила пропорциональна смещению(например, сила упругости), то получаем
колебательное движение. Рассмотрим частный
случай одномерного движения, которое
происходит под действием квазиупругой силы F= kx, где х – изменение длины пружины (r=x).
Уравнение движения имеет следующий вид:
m x kx
С учетом сил трения Fтр = - r V, где
29.01.2017
x V
m x kx rx
46
47.
Это дифференциальное уравнение 2-гопорядка, однородное.
k
2
x x x 0 x 0
m
Его решение известно из курса средней
школы и имеет вид (это уравнение
колебательного движения):
x A cos( 0t )
А- амплитуда колебаний, ω0 - циклическая
29.01.2017
частота,
φ-начальная фаза.
47
48. ФАЗОВЫЙ ПОРТРЕТ
Итак смещение точки при колебательномдвижении имеет вид:
x A cos( 0t )
Найдем ее скорость
dx
v
0 A sin( 0t )
dt
29.01.2017
48
49.
Преобразуем уравнения в видеx
cos( 0t )
A
v
sin( 0t )
A 0
Возведем в квадрат и сложим
x 2
v 2
( ) (
) 1
A
A 0
29.01.2017
49
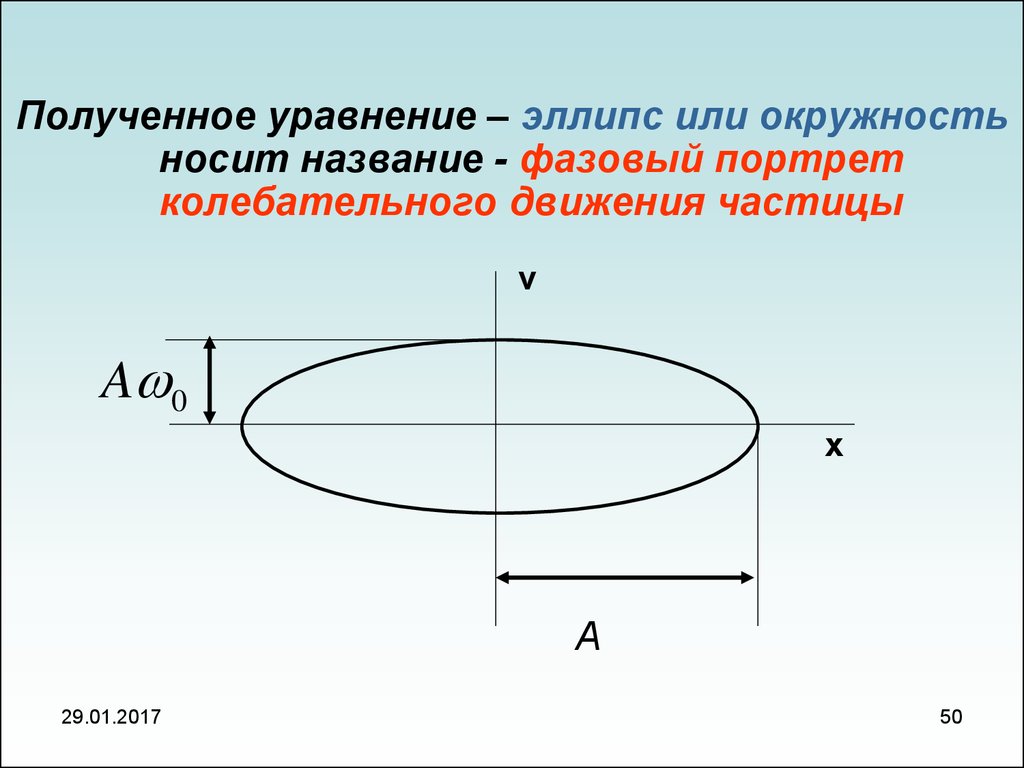
50.
Полученное уравнение – эллипс или окружностьносит название - фазовый портрет
колебательного движения частицы
v
A 0
x
A
29.01.2017
50
51.
Если уравнение для скорости умножить намассу частицы, то получим зависимость
импульса частицы р от координаты х. В этом
случае площадь эллипса равна энергии
колебательного движения за один период
S pdx Аm 0 A
29.01.2017
площадь эллипса равна
произведению его полуосей, умноженной на
51
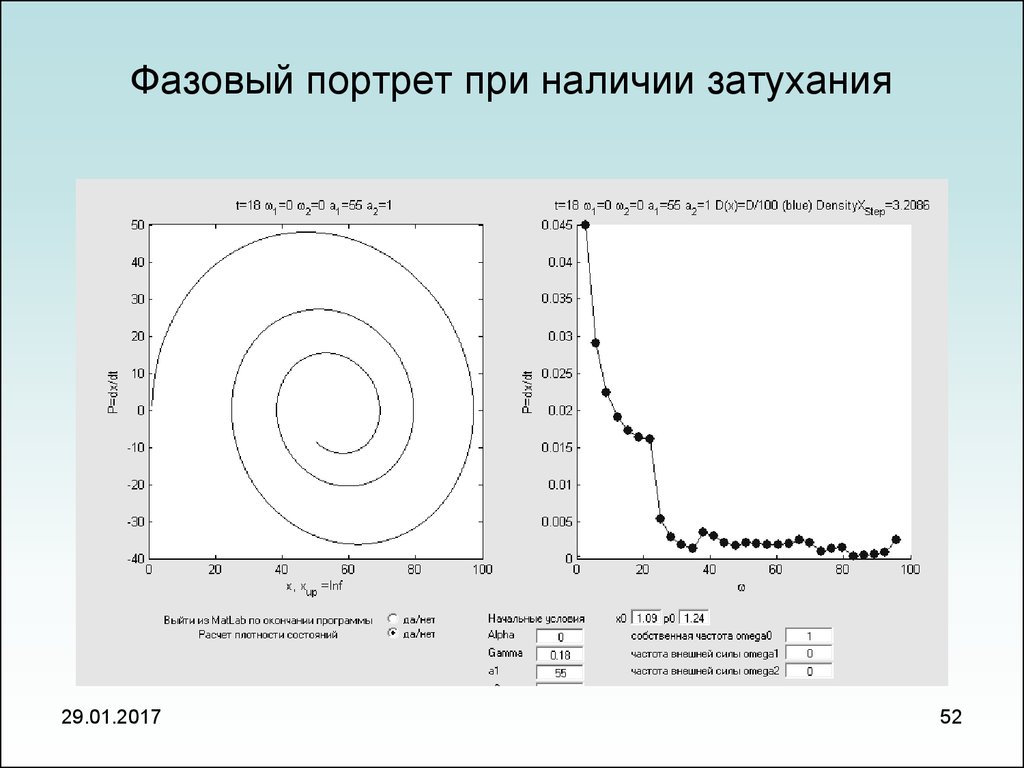
52. Фазовый портрет при наличии затухания
29.01.201752
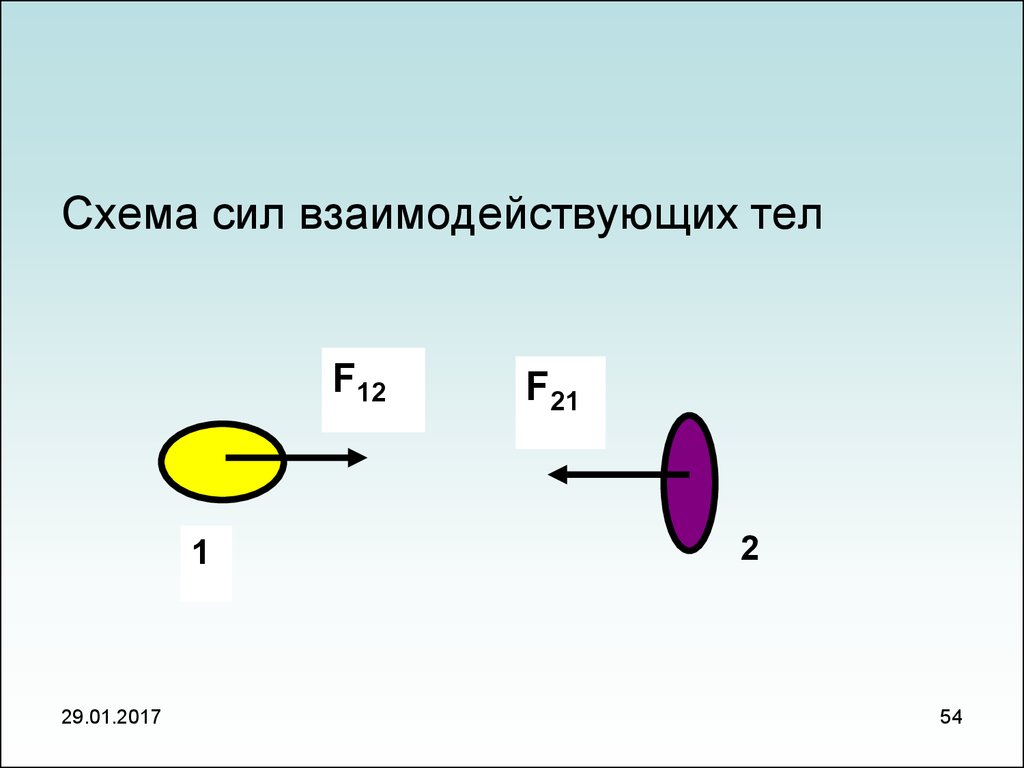
53. Третий закон Ньютона
Третий закон утверждает: если тело 1действует на тело 2 с силой F12, то в свою очередь
тело 1 обязательно действует на тело 2 с силой F21,
равной по величине и противоположной по знаку
силе F ; обе силы направлены вдоль одной
прямой. Третий закон отражает тот факт, что сила
есть результат взаимодействия двух различных
тел.
12
29.01.2017
53
54.
Схема сил взаимодействующих телF12
1
29.01.2017
F21
2
54
55. Закон сохранения импульса и энергии
Выполняется для замкнутой системы тел.Система считается замкнутой, если внешнее
воздействие мало по сравнению с
внутренними силами. Или внешнее
воздействие полностью отсутствует или
пренебрежимо мало.
Pi const
N
U Ek const
i 1
29.01.2017
55
56. 3.7. Закон сохранения импульса
Механическаясистема
называется
замкнутой (или изолированной), если на неё не
действуют внешние силы, т.е. она не
взаимодействует с внешними телами.
Строго говоря, каждая реальная система тел всегда
не замкнута, т.к. подвержена, как минимум воздействию
гравитационных сил. Однако если внутренние силы гораздо
больше внешних, то такую систему можно считать
замкнутой (например – Солнечная система).
Для замкнутой системы равнодействующий
вектор внешних сил тождественно равен нулю:
dp
F 0,
dt
(3.7.1)
57.
nотсюда
p mi υc const.
i 1
(3.7.2)
Это есть закон сохранения импульса: импульс
замкнутой системы не изменяется во времени.
Импульс системы тел может быть представлен в виде
произведения суммарной массы тел на скорость центра
инерции:
тогда
c
p m ,
m const.
(3.7.3)
c
При любых процессах, происходящих в
замкнутых системах, скорость центра инерции
сохраняется неизменной.
Закон сохранения импульса является одним из
основных законов природы. Он был получен как следствие
законов Ньютона, но он справедлив и для микрочастиц и
для релятивистских скоростей, когда
c

















































 Физика
Физика








