Михаил Юрьевич Лермонтов. Три пальмы (восточное сказание)

1.

Часть 3
физика
Михаил Юрьевич
Лермонтов
Три пальмы
(восточное сказание)
Движение тела, брошенного
под углом к горизонту.
Интегрированный урок физики и литературы
Учитель физики:
Яковлева Т. Ю.
Учитель литературы:Шаповалова Н.Э.
Школа № 285
Санкт - Петербург

2.

Лермонтов, М.Ю. Три пальмы рис. А.Н. Комарова.
- М.: Типография т-ва И. Д. Сытина, 1915. - 20 с

3.

И, стан худощавый к луке наклоня,
Араб горячил вороного коня.
И конь на дыбы подымался порой,
И прыгал, как барс, пораженный стрелой;

4.

Арабская лошадь
Арабская чистокровная порода, самая чистая и самая древняя, её считают
одной из самых красивых пород лошадей во всём мире. Изображения
лошадей в средневековом классическом искусстве доказывают, что на
Аравийском полуострове арабская порода лошадей жила за две-три
тысячи лет до Христа. Они приобрели огромную выдержку,
неприхотливость, способность к выживанию в неблагоприятных
климатических условиях, поскольку разводились и жили в пустынной
местности. В первую очередь арабская лошадь использовалась как
орудие войны, также как и другие лошади в то время в большинстве
цивилизаций. Благодаря сильной коннице бедуины атаковали вражеские
племена, захватывала их стада коз, овец, верблюдов, преумножая
богатство собственного племени. Подобные рейды были возможны только
при условии, если нападающий был способен быстро и неожиданно
напасть, и молниеносно скрыться от погони.

5.

В России арабские лошади появились в период правления Ивана
Грозного. Много лошадей этой породы завезли во второй половине
18 века. Самых лучших собрали в поместьях графа А.Г.ОрловаЧесменского.
Во всем мире и сейчас разводят чистокровных
арабских лошадей. Высота арабского коня 144 - 152 см. в холке.
Окрас белый, вороной или гнедой. Строение тела: "щучий" профиль;
красивая изящная голова; широкий лоб; маленькие уши; широкие
ноздри; большие выразительные ясные глаза; длинное, с
выраженной холкой сильное плечо; красиво изогнутая шея; глубокое
тело; широкая глубокая грудь; высоко посаженый хвост; короткая
ровная спина; длинные шелковистые хвост и грива; прочные копыта;
стройные, словно точеные, ноги. Уникальный профиль арабского
скакуна определяется строением его скелета, по некоторым
параметрам отличающегося от лошадей других пород. У арабов 5
поясничных позвонков (у остальных лошадей 6); 16 хвостовых
позвонков (у остальных лошадей 18); 17 ребер (у остальных
лошадей 18).

6.

Лошади чистокровной породы не превзойдены по резвости, их
нормой считается галоп со скоростью 1 км в минуту. На
коротких и средних дистанциях (до 2800 м) современные
чистокровные лошади развивают среднюю скорость около 60
км/ч, на длинных дистанциях (свыше 3000 м) они скачут со
скоростью 55 км/ч. Абсолютный рекорд скорости среди всех
пород домашней лошади принадлежит чистокровному
жеребцу Бич Рэкиту, который в Мехико на дистанции в
409,26 м (1/4 мили) развил скорость 69,69 км/ч. Участвовать в
скачках с чистокровными лошадьми запрещено лошадям
других пород, поскольку любая чистокровная лошадь на
порядок сильнее и резвее любой другой лошади.

7.

Скорость лошади зависит от способа шага. Так, например, галоп считается
традиционным шагом лошади, скорость которой при этом достигает 15-20 км в час.
По характеру движения и быстроте галоп подразделяется на манежный (при котором
скорость лошади составляет в среднем 300 метров в минуту), укороченный (400-700
м/мин) и резвый (более 1000 м/мин). Если же лошади предстоит пройти длинную
дистанцию, то она может развить скорость до 60 км в час. Стоит отметить, что
скорость чистокровной лошади, также как и прочие основные показатели, как
минимум, на один порядок выше, чем у животного любой другой породы.

8.

И, стан худощавый к луке наклоня,
Араб горячил вороного коня.
И конь на дыбы подымался порой,
И прыгал, как барс, пораженный стрелой;
И белой одежды красивые складки
По плечам фариса вились в беспорядке;
И, с криком и свистом несясь по песку,
Бросал и ловил он копье на-скаку.
Фарис (араб.) — всадник, наездник.
Фарь, фарис, вероятно, через ср.-греч. , "арабская
лошадь" из араб. faris "конь", “породистый скакун”.

9.

Метание копья
В настоящее время для проведения соревнований
используют полые металлические копья с веревочной
обмоткой у центра тяжести. Все копья для мужчин 800 г,
длина 260-270 см; для женщин соответственно 600 г и 220230 см, Разбег у метателей копья состоит из 14-17 беговых
шагов, 4-6 из которых приходятся на бросковые шаги.
Предварительная часть разбега у метателей копья
начинается с постепенным увеличением его скорости.
Максимальной скорости спортсмен достигает к началу
бросковых шагов. Спортсмены высокого класса в этой
части разбега развивают скорость 8 м/с. У сильнейших
метателей копья угол наклона туловища в исходном
положении для выполнения броска достигает 50°.
Сильнейшие копьеметатели мира выпускают копье с
начальной скоростью 32 ± 3 м/с под углом 35 ± 3°.

10.

Метание копья
Анализ
финального
движения
копьеметателя
показывает,
что
величина скорости вылета копья
формируется в основном за счет двух
звеньев
двигательного
аппарата
спортсмена:
движения
плечевого
сустава метающей руки относительно
опоры; движения кисти метающей
руки относительно плечевого сустава.
Скорости движения плечевого сустава
и кисти метающей руки суммируются,
что создает величину начальной
скорости вылета копья. Величина
скорости движения плечевого сустава
находится в прямой зависимости от
скорости
разбега
спортсмена,
Матти Ярвинен (Финляндия) выполняет набранной в предварительной части и
попытку в метании копья. Олимпийские сохраненной в бросковых шагах.
игры 1932 года.

11.

Метание копья
Копье получает начальную скорость вылета, и ему
задаются:
определенный угол вылета, который
29° до 36°;
колеблется от
высота траектории, с наивысшей точкой — 14 - 17 м;
время полета — 3,5 - 4,5 с;
начальная скорость копья — 30 - 32 м/с (при
результатах свыше 80 м).

12.

Метание копья
Известные метатели копья имеют совершенно разное
телосложение
и
физические
данные,
например,
рекордсмен мира Уве Хон обладал ростом 199 см и весом
114 кг, в то время, как другой рекордсмен, Сеппо Рети, 190
см и 89-120 кг. Нынешний рекордсмен мира, Ян Железный,
из Чехии, 185 см и 79-85 кг.
В 1984 году, восточногерманский копьеметатель Уве Хон
(Uwe Hohn) выполнил рекордный бросок на 104,80 м.
Такие дальние броски привели к необходимости изменить
снаряд, поскольку метание копья могло быть вообще
запрещено к проведению на стадионах по причине
небезопасности. В результате, центр тяжести у копья был
смещён вперёд, что привело к более раннему опусканию
носа снаряда, и сократило дальность броска примерно на
10 %. Схожий редизайн претерпел и женский вариант
копья (600 г против 800 г у мужчин) в 1999 году.

13.

Рекорды по метанию копья
Мировой рекорд у мужчин равен 98,48 м (1996 г.) и
принадлежит Яну Железны из Чехии. Рекорд у женщин
составляет 72.28 м (2008 г.) и был установлен Барбарой
Шпотаковой из Чехии. Олимпийский рекорд у мужчин
90,57 м (2008 г.) установил Андреас Торкильдсен из
Норвегии. Рекорды мира на копье старого образца: Уве
Хон ― 104,80 м и Петра Фёльке-Мейер 80,00 м. Мировой
рекорд Сеппо Рети в 1991 г. ― 96, 96 м.
Российская метательница копья
Мария Абакумова
установила мировой рекорд на Чемпионате мира по легкой
атлетике в 2011 году в Южной Корее. Абакумова показала
результат в 71,99 метров, установив не только новый
рекорд России, но и чемпионатов мира, а также показав
лучший результат сезона в мире.

14.

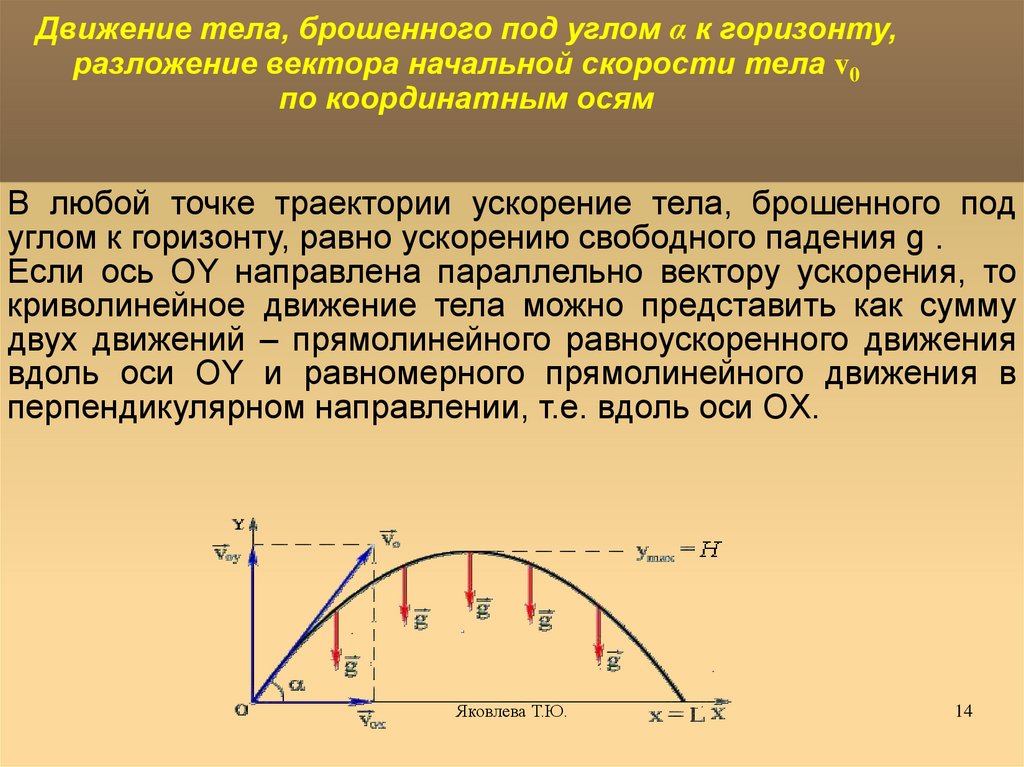
Движение тела, брошенного под углом α к горизонту,
разложение вектора начальной скорости тела v0
по координатным осям
В любой точке траектории ускорение тела, брошенного под
углом к горизонту, равно ускорению свободного падения g .
Если ось OY направлена параллельно вектору ускорения, то
криволинейное движение тела можно представить как сумму
двух движений – прямолинейного равноускоренного движения
вдоль оси OY и равномерного прямолинейного движения в
перпендикулярном направлении, т.е. вдоль оси OX.
Яковлева Т.Ю.
14

15.

Движение тела, брошенного под углом α
к горизонту, с начальной скоростью V0
Vx = V0 cosα
X = X0 + V0 cosα t
Vy = V0 sinα - gt
Y = Y0 +V0 sinα t gt2/2
V2 = Vx2 + Vy2
tgβ = Vy / Vx
Яковлева Т.Ю.
15

16.

“И, с криком и свистом несясь по песку,
Бросал и ловил он копье на-скаку.»
Задача
Копье брошено с начальной скоростью V = 32 м/с под углом
α = 35° к горизонту.
Найти:
1) Время полета t;
2) Дальность полета L;
3) Максимальную высоту подъёма Нмах;
4) Скорость V в момент, когда копье достигает Нмах;
5) Скорость при приземлении V.
sin35º = 0,573; cos35º = 0,819;
sin70º = 0,94 .
Яковлева Т.Ю.
16

17.

Задача на движение тела, брошенного
под углом α к горизонту
1) Определить полное время полета t тела можно из двух
уравнений:
при падении тела на землю через время t
Y = Y0 + V0 sinα t — gt2/2 = 0
или
в верхней точке траектории через время t/2
Vy = V0 sinα — gt/2 = 0.
Полное время полета
t = 2V0 sinα /g=2·32·0,573/9,8=3,74 (с).
Яковлева Т.Ю.
17

18.

Задача на движение тела, брошенного
под углом α к горизонту
2) Дальность полета L = X - X0 = V0 cosα t
Подставим значение времени полета t.
Тогда
L = V02 2sinα cosα /g = V02 sin2α /g =
= 322·0,94 /9,8 = 98,2 (м).
Максимальная дальность полета Lmax достигается
при угле α = 45о (sin2α = 1)
Lmax = V02 /g
Яковлева Т.Ю.
18

19.

Задача на движение тела, брошенного
под углом α к горизонту
3) Максимальная высота подъёма Нмах
соответствует моменту времени t /2,
где
t = 2V0 sinα /g
Нмаx = Y - Y0 = V0 sinα t /2 - gt2 /8 =
= V02 sin2α /2g =
= 322·0,5732 /(2·9,8) = 17,15 (м).
Яковлева Т.Ю.
19

20.

Задача на движение тела, брошенного
под углом α к горизонту
4) В момент времени t /2, когда копье
достигает максимальной высоты Нмах ,
проекция скорости на вертикальную ось OY
Vy = 0.
Скорость тела V
V = (Vx2 + Vy2)1/2 = Vx
V = Vx = V0 cosα = 32·0,819 = 26,2 (м/с).
Яковлева Т.Ю.
20

21.

Задача на движение тела, брошенного
под углом α к горизонту
5) Скорость при приземлении в момент времени t = 2V0 sinα /g
V = (Vx2 + Vy2)1/2,
где Vx = V0 cosα
Vy = V0 sinα - gt = - V0 sinα.
V = (V02cos2α + V02sin2α)1/2= V0 = 32 (м/с),
Угол между направлением скорости и горизонтом
определим по формуле
tgβ = Vy / Vx = (- V0 sinα) /( V0 cosα) = - tgα,
β = arctg (Vy / Vx) = - α.
По величине конечная скорость равна начальной (V = V0
),
по направлению они отличаются (α = - β).
Яковлева Т.Ю.
21

22.

Задача
“И, с криком и свистом несясь по песку,
Бросал и ловил он копье на-скаку.»
На коротких дистанциях чистокровные лошади
развивают среднюю скорость около 60 км/ч.
Наездник из стихотворения М.Ю. Лермонтова «Три
пальмы» бросал и ловил копье на-скаку.
Предположим, что копье бросалось под углом 45
градусов к горизонту. Определите начальную
скорость копья, время его полета и расстояние,
которое должна преодолеть лошадь, чтобы
наездник сумел поймать копье.
Яковлева Т.Ю.
22

23.

Задача на движение тела, брошенного
под углом α к горизонту
1) Vлошади = Vx,
Начальная скорость тела
V0 = Vлошади/cosα = 16,66/0,7 = 23,8 м/с.
2) Определить время полета t тела: Vy = V0 sinα — gt/2 = 0.
t = 2V0 sinα /g
3) Дальность полета L = Vлошади t = V0 cosα t = V02 sin2α
/g
При угле α = 45о
2 / 9,8 = 57,8 м.
Lmax = V02 /g =Яковлева
23,8Т.Ю.
23

24.

Контрольные вопросы
1. Дайте определение материальной точки. Для чего введено
понятие «материальная точка»? В каких случаях твёрдое тело
можно заменить материальной точкой?
2. Для чего вводится система отсчёта?
3. Дайте определение криволинейного движения.
4. Как направлена мгновенная скорость при криволинейном
движении?
5. Как записывается уравнение скорости в проекциях на
координатную ось?
6. Как производят сложение скоростей?
7. Как записывается уравнение движения?
8. Чему равно и куда направлено ускорение тела, брошенного
Яковлева Т.Ю.
24
под углом к горизонту?

25.

Домашнее задание
1. Рассмотреть движение тела, брошенного под углом α с наклонной
плоскости. Между горизонтом и наклонной плоскостью угол β. Систему
координат поставить на наклонную плоскость (ось ОХ параллельна
наклонной плоскости, ось ОY — перпендикулярна ей).
X = X0 + V0 cosα t + g sinβ t2/2
Y = Y0 +V0 sinα t - g cosβ t2/2
Vx = V0 cosα + g sinβ t
Vy = V0 sinα - g cosβ t
V2 = Vx2 + Vy2
2. Выучить наизусть стихотворение М.Ю.Лермонтова «Три пальмы».
Яковлева Т.Ю.
25

26.

Спасибо за внимание!
Яковлева Т.Ю.
26