Решение задач движение тела, брошенного под углом к горизонту

1.

Решение задач
Движение тела, брошенного под
углом к горизонту

2.

Повторение

3.

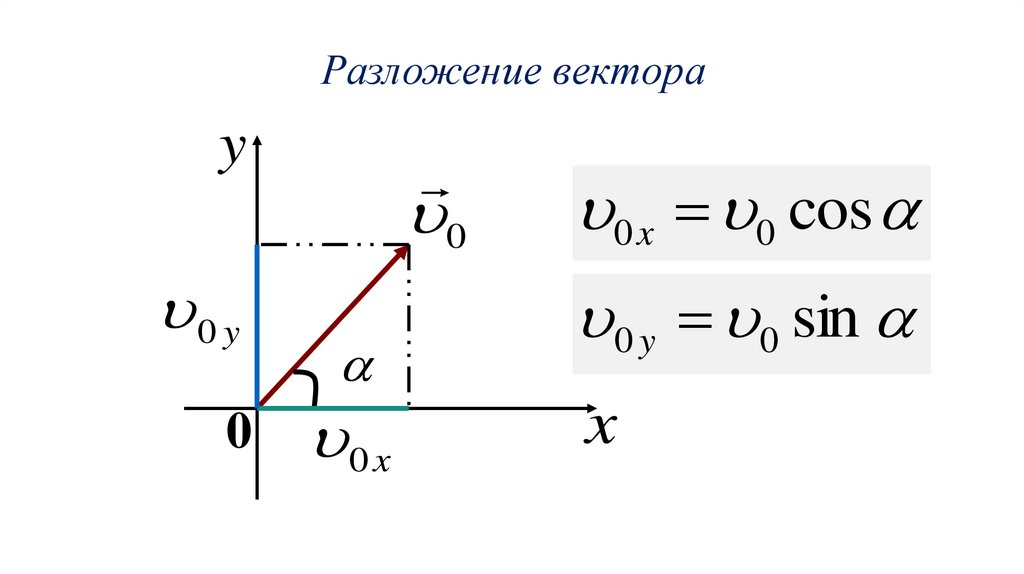
Разложение вектора
y
0 y
0
0
0 x
0 x 0 cos
0 y 0 sin
x

4.

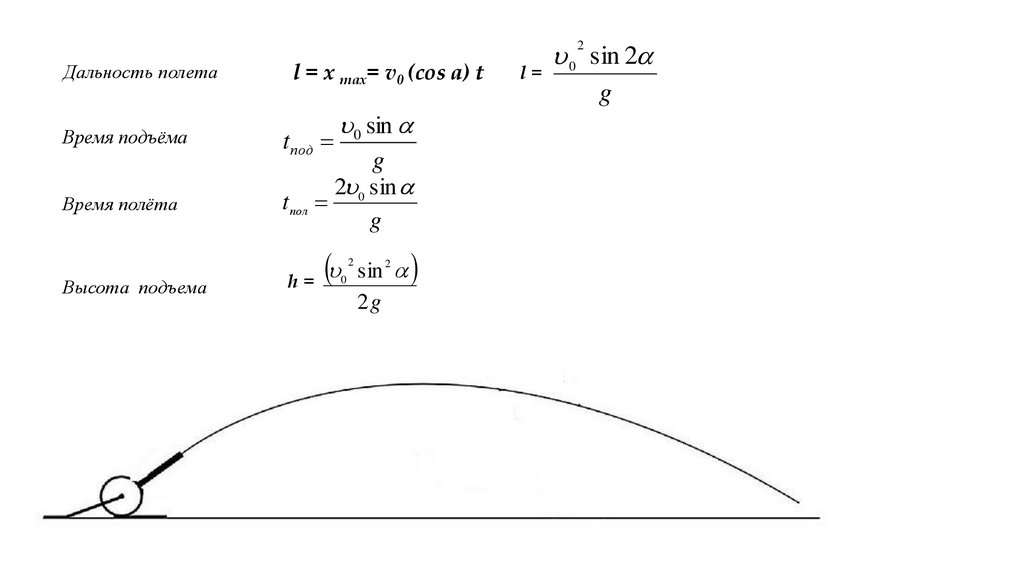
0 sin 2
2
Дальность полета
Время подъёма
Время полёта
Высота подъема
l = х max= v0 (cos a) t
t под
0 sin
g
2 0 sin
tпол
g
h=
2
0
sin 2
2g
l=
g

5.

Задача 1
Тело брошено горизонтально с высоты 4 м со скоростью 30 м/с. Определите мгновенные проекции вектора
скорости на оси ОХ и ОУ.
Решение
Для решения задачи вспомним, что проекция вектора это скалярная величина (число), равная
длине геометрической проекции вектора.
Опускаем из конца вектора перпендикуляры на оси и вычисляем:
Получаем:

6.

Задача 2
Тело брошено под углом 30° к горизонту со скоростью 20 м/с. Вычислите проекции скорости на оси ОХ и OY.
Решение
Для решения задачи вспомним, что проекция вектора это скалярная величина
(число), равная длине геометрической проекции вектора.
Опускаем из конца вектора перпендикуляры на оси и вычисляем:
Ответ: 10 м/с

7.

Задача 3
Тело брошено под углом 45° к горизонту со скоростью 40 м/с. Определите проекции вектора скорости на оси ОХ и OY.
Решение
Для решения задачи вспомним, что проекция вектора это скалярная
величина (число), равная длине геометрической проекции вектора.
Опускаем из конца вектора перпендикуляры на оси и вычисляем:
Получаем:
Ответ:Vx =28,2 м/с Vy = 28,2 м/с

8.

Задача 4.
Два тела брошены вертикально вверх из одной точки одно вслед за другим с интервалом времени, равным Δt,
с одинаковыми скоростями V0. Через какое время t после бросания первого тела они встретятся?
Решение задачи
Из анализа условия задачи, ясно, что первое тело поднимется на
максимальную высоту и на спуске встретится со вторым телом.
Запишем законы движения тел:
h1=V0t−gt2/2
h2=V0(t−Δt)−g(t−Δt)2/2.
В момент встречи h1=h2, откуда сразу получаем
t=V0/g+Δt/2

9.

Задача 5
Из точки А свободно падает тело. Одновременно из точки В под углом α к горизонту бросают другое тело так,
чтобы оба тела столкнулись в воздухе. Показать, что угол α не зависит от начальной скорости V0 тела,
брошенного из точки В, и определить этот угол, если H/S=√ 3. Сопротивлением воздуха пренебречь.
Решение задачи
Оба тела могут встретиться на линии ОА (см. рис.) в точке С. Разложим
скорость V0 тела, брошенного из точки В, на горизонтальную и вертикальную
составляющие:
V0x=V0 cosα;
V0y=V0 sinα.
Пусть от начала движения до момента встречи пройдет время t=S/V0x=S/V0cosα.
За это время тело из точки А опуститься на величину H−h=gt2/2,
а тело из точки В поднимется на высоту h=V0yt−gt2/2=V0sinα t−gt2/2.
Решая последние два уравнения совместно, находим H=V0sinαt.
Подставляя сюда ранее найденное время, получим tgα=H/S=√3
т.е. угол бросания не зависит от начальной скорости.
Ответ: α=600

10.

Задача 6.
С башни брошено тело в горизонтальном направлении со скоростью 40 м/с. Какова скорость тела через 3 с
после начала движения? Какой угол образует с плоскостью горизонта вектор скорости тела в этот момент?
Решение задачи
Тело одновременно участвует в двух движениях: равномерно в
горизонтальном направлении со скоростью V0 и в свободном падении
со скоростью:
Vy=gt.
Тогда полная скорость тела есть
V=√V02+g2t2 =50 м/с.
Направление вектора скорости определяется углом α. Из рисунка видим, что:
cosα=V0/V=V0 / √V02+g2t2 = 0.8
Ответ: α=370

11.

Задача 7.
Мяч бросают с крыши, находящейся на высоте 20 м от поверхности земли. Его начальная скорость равна 25 м/с
и направлена:
А. горизонтально;
Б. вверх под углом 30° к горизонту;
В. вниз под углом 30° к горизонту. Чему равна дальность полета по горизонтали?
Решение задачи
А.
Б.
при падении у = 0, t1 = 36с, t ≥ 0, следовательно:
В.
у = 0, t1 = 1,1с, но t ≥ 0, следовательно, t2 = -3,5с t = 1,1c

12.

Задача 8
Из старинной пушки, ствол которой установлен под углом 45° к горизонту, выпущено ядро со скоростью 141 м/с.
а. распишите проекции скорости на горизонтальное и вертикальное направление.
б. вычислите, через сколько времени тело упадет на землю.
в. рассчитайте дальность полета снаряда.
Решение задачи
а
б
в
когда тело упадет на землю, его скорость vy' будет равна – vy:

13.

Задача 9
Снаряд вылетел из дальнобойной пушки с начальной скоростью 1000 м/с под углом 30° к горизонту. Сколько
времени снаряд будет находиться в воздухе? На каком расстоянии от пушки он упадет на землю? Пушка и точка
падения снаряда находятся на одной горизонтали. Какую скорость будет иметь снаряд в момент падения на землю?
Решение
в момент падения vy'= - vy

14.

Задача 10
Снаряд вылетает из орудия с начальной скоростью 490 м/с под углом 300 к горизонту. Определить высоту,
дальность и время полета снаряда, не учитывая его вращение и сопротивление воздуха.
Решение
Проекции скорости на оси Х и Y:
в момент падения vy'= - vy, тогда:

15.

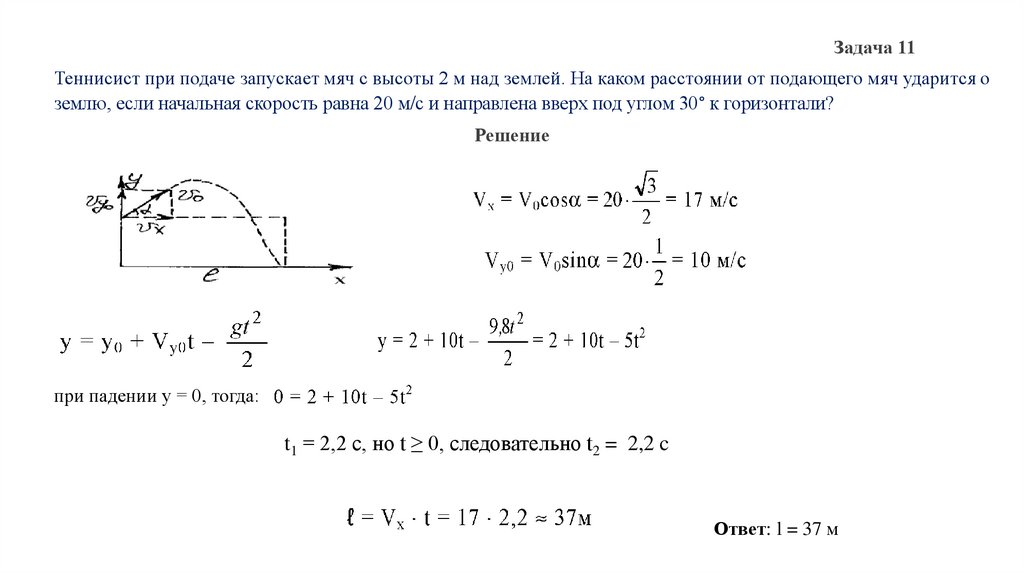
Задача 11
Теннисист при подаче запускает мяч с высоты 2 м над землей. На каком расстоянии от подающего мяч ударится о
землю, если начальная скорость равна 20 м/с и направлена вверх под углом 30° к горизонтали?
Решение
при падении у = 0, тогда:
t1 = 2,2 c, но t ≥ 0, следовательно t2 = 2,2 c
Ответ: l = 37 м

16.

Задача 12
Миномет установлен под углом α=60° к горизонту на крыше здания, высота которого h=40 м. Начальная скорость
v0 мины равна 50 м/с. Требуется: 1) написать кинематические уравнения движения и уравнения траектории и
начертить эту траекторию с соблюдением масштаба; 2) определить время τ полета мины, максимальную высоту
H ее подъема, горизонтальную дальность s полета, скорость v в момент падения мины на землю.
Сопротивлением воздуха пренебречь.
Решение