Игровая стратегия

1.

ЭКСПРЕСС-ПОДГОТОВКА
Часть IV
КЕГЭ-2023
19-20-21
игровая стратегия, одна куча

2.

Задания 19-21
• Описать игровую стратегию для заданий с
кучками равносильно построению
ориентированного двудольного графа, где
состояния куч (вершины) разбиты на две
группы.
К 1-й группе отнесем вершины, из которых
можно попасть в «выигрышные» поля и поля
2-й группы, а из вершин 2-й группы все ходы
должны вести в вершины 1-группы.
Такой способ решения называется методом
«раскраски».

3.

Опишем решение стандартной задачи на одну кучу «ручным» способом.
Вершины, в которые можно попасть из заданной за один ход будем считать смежными.
Ходы игроков будем называть тактами (1 такт – 1-й ход Пети, 2 такт – 1-й ход Вани, 3
такт – 2-й ход Пети, 4 такт – 2-й ход Вани и т.д.)
На каждом такте мы будем определять цвет раскраски для «новые» вершин, причем
для нечётных тактов красить будем в «нечётные» цвета, а для чётных в «чётные» цвета.
До начала игры выполним Такт 0.
Шаг 0. Определим множество вершин A0=[43,44,…126,…] – это вершины, попадая в
которые игрок выигрывает. Будем считать, что эти вершины мы окрасили в «чётный
цвет» с номером 0.

4.

Опишем решение стандартной задачи на одну кучу «ручным» способом.
Такт 1. Определим множество вершин A1, таких, что у них есть смежные в A0. Нетрудно понять, что
A1= [15,16,…42]. Будем считать, что эти вершины мы окрасили в «нечётный цвет» с номером 1. Для
вершин из A1 у Пети существует «выигрышная стратегия» (ВС) позволяющая выиграть за один ход.
Такт 2. Определим множество вершин A2, таких, что из ВСЕ их смежные в A1. Нетрудно понять, что
такая вершина одна и A2= [14]. Будем считать, что эту вершину мы окрасили в «чётный цвет» с
номером 2. Для вершин из A2 «выигрышная стратегия» существует для Вани и позволяет ему
выиграть за один ход при любом ходе Пети.
Такт 3. Определим множество вершин A3, таких, что из них есть смежные в A2. Нетрудно понять,
что A3= [10,13] (10+4=14; 13+1=14). Будем считать, что эти вершины мы окрасили в «нечётный
цвет» с номером 3. Для вершин из A3 у Пети нет возможности выиграть первым ходом, но
существует «выигрышная стратегия» (ВС) позволяющая выиграть 2-м ходом.
Такт 4. Определим множество вершин A4, таких, что из ВСЕ их смежные в A1или A3. Нетрудно
понять, что таких вершин две и A2= [9,12]. Будем считать, что эту вершину мы окрасили в «чётный
цвет» с номером 4. Для вершин из A4 «выигрышная стратегия» существует для Вани и позволяет
ему выиграть первым или вторым ходом.
Этот процесс можно продолжать, но для ответов на задания множеств A1, A2, A3, A4 достаточно.

5.

Шаг 1. Получение смежных вершин и начальное заполнение списка «раскраски»
[0;124] –> None; [125;163] -> 0 [163;3*125-1] -> -1 (-1 - это поле «проигрыша»)
Добавляем часть Основного блок с обработкой
нечётных тактов
A1
С помощью ‘copy-paste’
добавляем обработку чётных
тактов

6.

Задание 19. Ответ: минимальное значение из A2 = 14
Задание 20. Ответ: минимальные значение из A3 = 10, 13
Задание 21. Ответ: минимальное значение из A4 = 9
Построим программное решение, причем для каждого S из отрезка [1;42] определим
игрока имеющего «выигрышную стратегию» и номер хода (такта) гарантирующий
победу.

7.

Создание программного решения
Шаг 1. Создание списка для записи цветов вершин:
Шаг 2. Процедура получения смежных вершин:
Шаг 3. Цикл по тактам от 1 до N (игра не может продолжаться более N-1 хода):
Для каждого такта определяем:
список для «новых» вершин (Ai)
Организуем перебор всех вершин без раскраски :
Если такт нечётный,
то пытаемся раскрасить в «нечётный» цвет
Если такт чётный,
то проверяем на раскраску в «чётный» цвет
печатаем номер такта и список «новых» вершин
Если список пустой, то завершаем работу
.
Вершину красим в «нечётный» цвет, если хотя бы ОДНА из смежных вершин
окрашена в «чётный» цвет.
Вершину красим в «чётный» цвет, если ВСЕ смежные вершины окрашены в
«нечётный» цвета.

8.

Текст программы с комментариями и пояснениями

9.

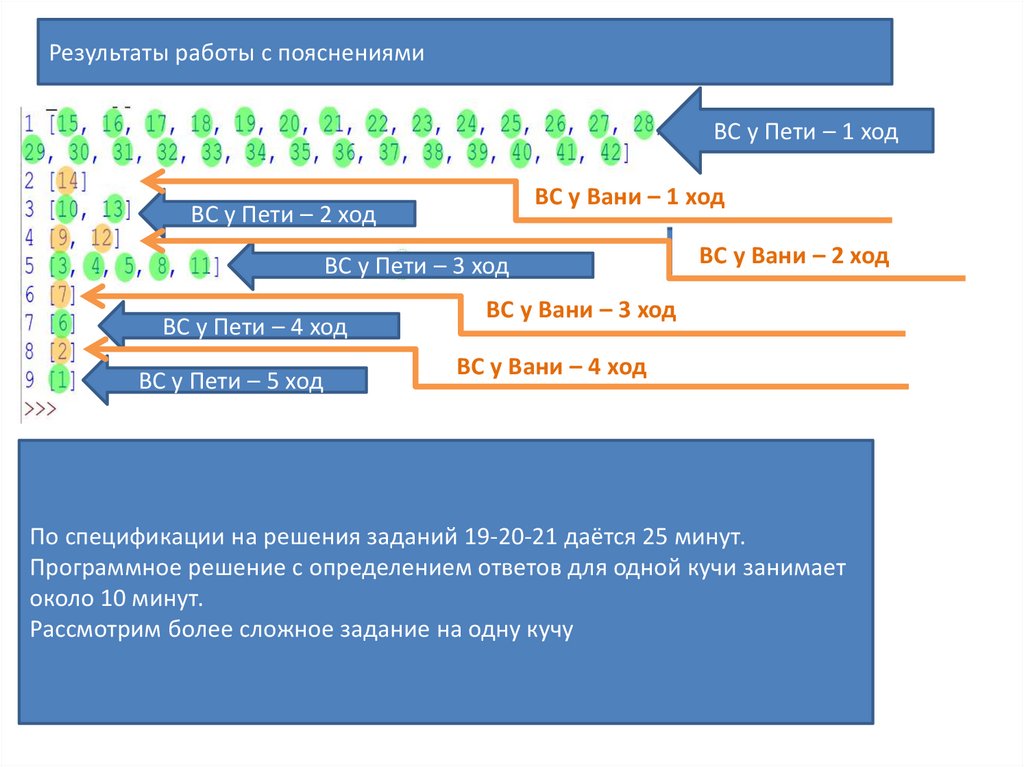
Результаты работы с пояснениями
ВС у Пети – 1 ход
ВС у Вани – 1 ход
ВС у Пети – 2 ход
ВС у Пети – 3 ход
ВС у Пети – 4 ход
ВС у Пети – 5 ход
ВС у Вани – 2 ход
ВС у Вани – 3 ход
ВС у Вани – 4 ход
По спецификации на решения заданий 19-20-21 даётся 25 минут.
Программное решение с определением ответов для одной кучи занимает
около 10 минут.
Рассмотрим более сложное задание на одну кучу

10.

Шаг 1. Получение смежных вершин и начальное заполнение списка «раскраски»
[0;124] –> None; [125;163] -> 0 [163;3*125-1] -> -1 (-1 - это поле «проигрыша»)
Добавляем часть Основного блок с обработкой
нечётных тактов
A1
С помощью ‘copy-paste’
добавляем обработку чётных
тактов

11.

Текст программы и результат

12.

Вопросы и фрагменты результатов
S=122 (122+2=124)
Ответы:
19 = 122
20 = 31 118
21 = 113
Зона выигрыша сложением
Петя должен попасть сюда

13.

Задача с необычным условием
Шаг 1. Получение смежных вершин и начальное заполнение списка «раскраски»
[0;99] –> None; [42] -> 0 (уже из 80 за 4 такта в 42 не попасть)
Добавляем Основной блок (стандартный)

14.

Вопросы и фрагменты результатов
Петя должен попасть в «строку 1»
Минимальное 35-7=28
Значения берем из «строки 3»
31,37
Значения берем из «строки 4»
50
Ответы:
19 = 28
20 = 31 37
21 = 50

15.

Задача с условием «последний ход проигрывает»
Шаг 1. Получение смежных вершин и начальное заполнение списка «раскраски»
[0;99] –> None; [100:199] -> -1 (красим в «нечётный», т.к. последний проигрывает)
Добавляем Основной блок
Просмотр тактов начинаем с 0 !!!

16.

Вопросы и фрагменты результатов. «Строка 0» – позиции из которых Ваня
выиграет, не совершив ни одного хода
Петя должен попасть в «строку 0» за счёт сложения
Минимальное 94+4=98
Значения берем из «строки 4»
86,87
Значения берем из «строки 3»
46 91
Ответы:
19 = 94
20 = 86 87
21 = 46 91

17.

Анализ.
• Предлагаемый способ – это по сути «обход
в ширину». Путем настройки нескольких
параметров можно решать очень широкий
класс задач. В большинстве случаев затраты
на решении не более 10 минут (по
спецификации на задания 19-20-21
отведено 25 минут
• Способ продолжает «общую линию»
решения заданий КЕГЭ 2023 года