Похожие презентации:
Частотные свойства цепей синусоидального тока. Резонанс напряжений
1. Дисциплина: Теоретические основы электротехники
2.
23. Лекция №11
Тема: Частотныесвойства цепей
синусоидального
тока. Резонанс
напряжений
4. Учебные вопросы
1. Понятие о резонансе впоследовательном колебательном
контуре.
2. Свойства цепи при резонансе
напряжений.
3. Частотные характеристики
последовательного колебательного
контура.
4. Избирательные свойства
последовательного колебательного
контура.
5. Литература
1. Бессонов Л.А.Теоретические основы
электротехники.
Электрические цепи:
учебник для бакалавров. –
М. : Издательство Юрайт,
2012, с. 106-114.
6. Режимы работы последовательной RLC-цепи
Векторные диаграммы напряжений и токовАктивно-индуктивный
Активно-ёмкостной
Активный
(резонанс напряжений)
7. Свойства активно-индуктивного режима последовательной RLC-цепи
Свойства активноиндуктивного режимапоследовательной RLC-цепи
xL xC
1
L
c
U L xL I U C xC I
0
- напряжение опережает ток
источника;
- цепь имеет индуктивный
характер;
8. Свойства активно-ёмкостного режима последовательной RLC-цепи
xL xCU L xL I U C xC I
1
L
c
0
- напряжение отстает от тока
источника;
- цепь имеет емкостной
характер;
9. Свойства режима резонанса напряжений последовательной RLC-цепи
xL xCU L xL I U C xC I
1
L
c
0
- напряжение на индуктивном и емкостном
элементах полностью компенсируют друг друга,
т.к. , а напряжение на резистивном элементе
становится равным напряжению источника и
совпадает по фазе с током;
- сопротивление цепи имеет чисто резистивный
характер;
10.
1. Резонанс в последовательномколебательном контуре
В радиотехнике актуальной является задача
выделения полезного сигнала и снижение уровня
помех.
Избирательные цепи или линейные узкополосные
частотные фильтры это электрические цепи,
которые из всей суммы колебаний различных
частот пропускают на выход только колебания с
относительно узкой полосой частот.
Такое свойство электрической цепи называется
избирательностью (селективностью).
Простейшими избирательными цепями является
последовательные и параллельные
колебательные контуры. Избирательность
колебательных контуров основана на явлении
резонанса.
11.
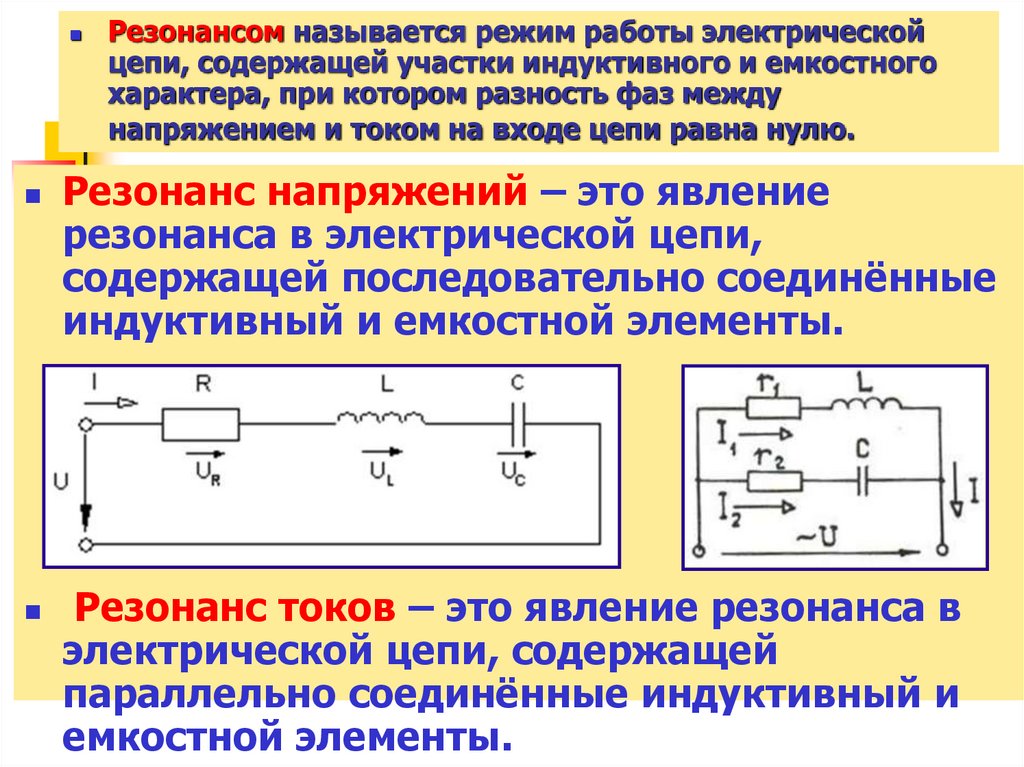
Резонансом называется режим работы электрическойцепи, содержащей участки индуктивного и емкостного
характера, при котором разность фаз между
напряжением и током на входе цепи равна нулю.
Резонанс напряжений – это явление
резонанса в электрической цепи,
содержащей последовательно соединённые
индуктивный и емкостной элементы.
Резонанс токов – это явление резонанса в
электрической цепи, содержащей
параллельно соединённые индуктивный и
емкостной элементы.
12. 1.1 Условия возбуждения резонанса напряжений
Полное комплексноесопротивление
колебательного
контура
Z
равно
сумме
трех
сопротивлений:
1
Z Ze j Z cos jZ sin
Z Z R Z L Z C R j ( x L xC ) R j 0 L
0 C
Из определения резонанса
следует, что при мнимая
часть комплексного
сопротивления равна нулю:
u i 0
Im[ Z ] Z sin xL xC 0 L
Основным условием возбуждения резонанса
напряжений в цепи гармонического тока является
равенство индуктивного и емкостного
сопротивления цепи:
1
0
0 c
x0 L x0C
13. 1.2 Характеристики резонанса напряжений
1. Резонансная частота:0 L
1
0С
0
1
LC
Резонансная частота определяется только
параметрами цепи, поэтому она часто называется
собственной частотой цепи.
2. При резонансе модуль реактивного сопротивления
индуктивности равен модулю реактивного
сопротивления емкости. Эти величины получили
название характеристического волнового
сопротивления ρ:
1
L
0 L
0 c
C
14. 3. Добротность колебательного контура Q – безразмерная величина, которая является отношением характеристического сопротивления
кактивному сопротивлению контура:
Q
R
Величина обычно составляет сотни Омов (100-300 Ом), а R –
единицы Омов. Поэтому добротность Q, как правило, составляет
величину в несколько десятков и сотен (50-300).
Добротность контура увеличивается с уменьшением
резистивного сопротивления контура и с увеличением
характеристического сопротивления.
4. Затухание контура - величина, обратная
добротности
1
R
d
Q
15. 1.3 Способы возбуждения резонанса
1 способ. При неизменных параметрах цепи(L = const, C = const) необходимо изменять
угловую частоту напряжения источника
питания (ω = var), приближая ее к собственной
частоте цепи:
0
2 способ. При неизменной угловой частоте напряжения
источника питания ( ω= const) необходимо изменять
собственную угловую частоту цепи, изменяя ее
параметры (L = var, C = var) и обеспечивая
приближение собственной частоты контура к частоте
напряжения источника питания:
0
16.
C=
const
при:
ω = const
L = const
при:
ω = const
L
=
const
при:
C = const
16
17.
2. Свойства цепи прирезонансе напряжений
1. Полное сопротивление цепи в резонансном
режиме имеет чисто резистивный характер,
равно сопротивлению резистивного элемента и
является минимальным:
Z R j ( x L xC )
Z Z R 2 ( x L xC ) 2
x0 L x0C
x 0 x 0L x 0C 0
Z0
R02 x02 R0 Z min
18.
+jjXL
-jXC
Z=R
+1
R
Треугольник
сопротивлений для
условия резонанса
18
19.
Свойства цепи прирезонансе напряжений
2. Ток в цепи при резонансе напряжений
является максимальным и по характеру
чисто активным, т.е. не имеет сдвига по
фазе по отношению к напряжению:
U
I0
Z0
U
U
U
I max
R0 Z min
R02 ( x0 L x0C ) 2
x0 L x0C
x0
0 u i arctg
arctg
0
R0
R0
20.
Свойства цепи прирезонансе напряжений
3. Коэффициент мощности цепи равен
единице, полная мощность равна
активной. Это означает, что ток в цепи
при резонансе совершает максимальную
полезную работу.
0 0
cos 0 1
P0 S0 cos 0 UI0 cos 0 UI0 S0
S0 P02 Q02 P02 (Q0 L Q0C )2 ( I 02 R)2 [( I 02 x0 L ) ( I 02 x0C )]2 I 02 R P0
21.
Свойства цепи прирезонансе напряжений
4. В цепи имеют место обратимые преобразования энергии
электрического и магнитного полей, причем интенсивность
этих преобразований одинакова: энергия электрического
поля конденсатора и энергия магнитного поля катушки
преобразуются одна в другую с одинаковой скоростью .
Q0 L I x Q0C I x 0
2
0 0L
2
0 0C
Q0 Q0 L Q0C 0
Q0C 0, Q0 L 0
Все колебания энергии (обратимые ее
преобразования) имеют место только в пределах
внешней цепи, возврата энергии к источнику нет.
22.
Свойства цепи прирезонансе напряжений
5. Энергия, потребляемая контуром от источника,
равна энергии, теряемой в активном
сопротивлении контура R. Колебательный
процесс в контуре без потерь должен иметь
незатухающий характер.
T
T
T
0
0
0
W П uidt 2U 0 cos( 0t ) 2I 0 cos( 0t ) dt 2RI 02 cos 2 ( 0t )dt RI 02T
23.
Свойства цепи прирезонансе напряжений
6. Действующие значения напряжений на реактивных
элементах равны между собой:
U
U 1
U 0 L U 0C I 0 x0 L I 0 x0C 0 L
R
R 0 c
U L
U LC U L
U U Q
R LC R C
R C
R
U 0 L U 0C 1 L
Q
U
U
R C R
Добротность контура показывает во сколько раз
напряжения на реактивных элементах контура
при резонансе превышает значение
приложенного к контуру напряжения.
24. Физический смысл добротности контура
WзапLI 02
L
WП
RI 02T
RT
1
2
T
f0
0
Wзап 0 L
1
Q
WП
2 R 2 R 2
Q 2
Wзап
WП
Добротность колебательного контура
характеризует свойство колебательного контура
запасать энергию в реактивных элементах, она
равна отношению энергии, запасаемой в
контуре, к энергии потребляемой контуром за
период колебаний, умноженному на 2π.
25. 3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ПОСЛЕДОВАТЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА
Зависимости от частоты параметров контура:x( ) xL ( ) xC ( )
Фазо-частотная
характеристика
1
L
x( )
c
( ) arctg
arctg
R
R
Амплитудно-частотные характеристики – это зависимости
действующих или амплитудных значений тока и
напряжения от частоты:
I ( )
U L ( )
U C ( )
26. Амплитудно-частотные характеристики
UI ( )
Z ( )
U
1 2
R ( L )
c
2
U L
U L ( ) I ( ) xL ( )
1 2
R ( L )
c
2
U C ( ) I ( ) xc ( )
U
1 2
c R ( L )
c
2
U
R2
1 2
(
1
)
2 2
2
L
LC
U
R 2 2c 2 ( 2 LC 1) 2
27.
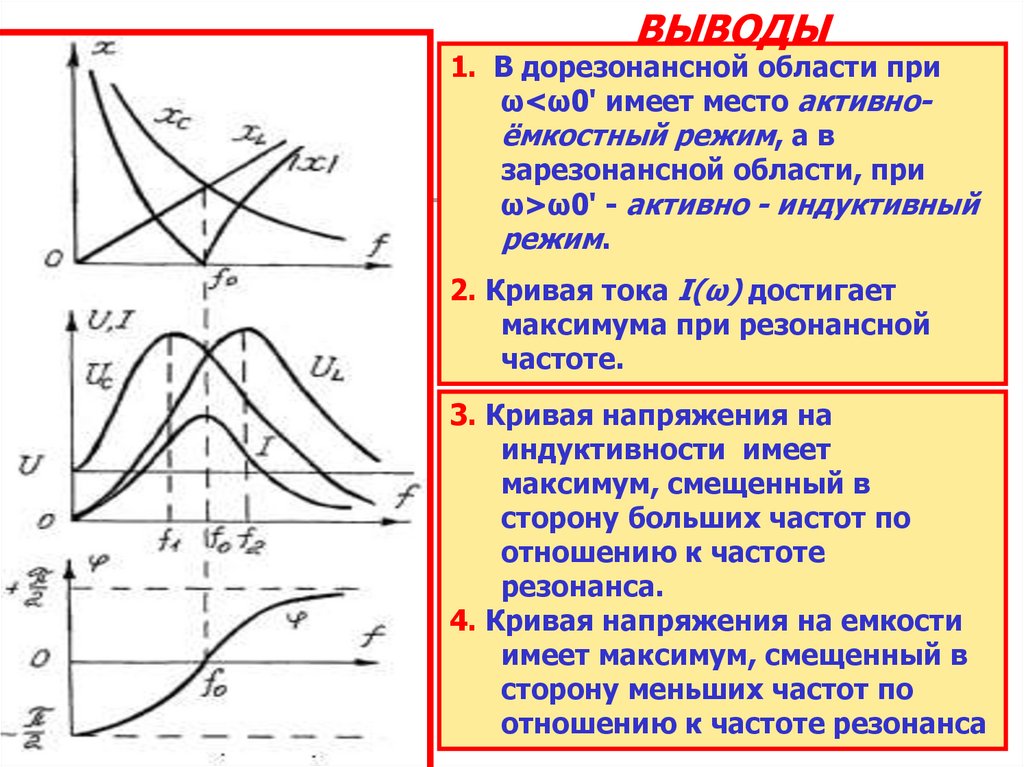
ВЫВОДЫ1. В дорезонансной области при
ω<ω0' имеет место активноёмкостный режим, а в
зарезонансной области, при
ω>ω0' - активно - индуктивный
режим.
2. Кривая тока I(ω) достигает
максимума при резонансной
частоте.
3. Кривая напряжения на
индуктивности имеет
максимум, смещенный в
сторону больших частот по
отношению к частоте
резонанса.
4. Кривая напряжения на емкости
имеет максимум, смещенный в
сторону меньших частот по
отношению к частоте резонанса
28. 4. Избирательные свойства последовательного колебательного контура. 4.1 Расстройки колебательных контуров
Абсолютная расстройка – разность между частотой колебаний,подводимых к контуру от источника, и резонансной частотой
контура
0
Относительная расстройка – отношение абсолютной расстройки к
резонансной частоте.
Обобщенная расстройка –
0
0
Q( )
0
Обобщенная расстройка для случая
малых расстроек -
2Q
0
29. 4.2 Нормированная амплитудно-частотная характеристика
4.2 Нормированная амплитудночастотная характеристикаI
U R
R
f( )
2
2
2
2
I0
0
R x U
R x ( )
xL xC 2
0 1 2
1
1 2
1 0
Z R x R 1 (
) R 1 2 ( L ) R 1 2 ( L
)
R
R
c
R 0
0 c
2
2
02 L2 0 2
R 1 2 ( )
R 0
0 L
0 2
Z R 1 Q ( ) R 1 2
0
2
Q
R
0
x
Q( )
0
R
30. Нормированная амплитудно-частотная характеристика наглядно показывает избирательные свойства контура
II0
1
0 2
1 Q ( )
0
2
I
I0
1
1 2
1
2
1 ( 2Q
)
0
Вывод: чем больше добротность Q, тем уже АЧХ
контура, и тем лучше избирательные свойства
цепи
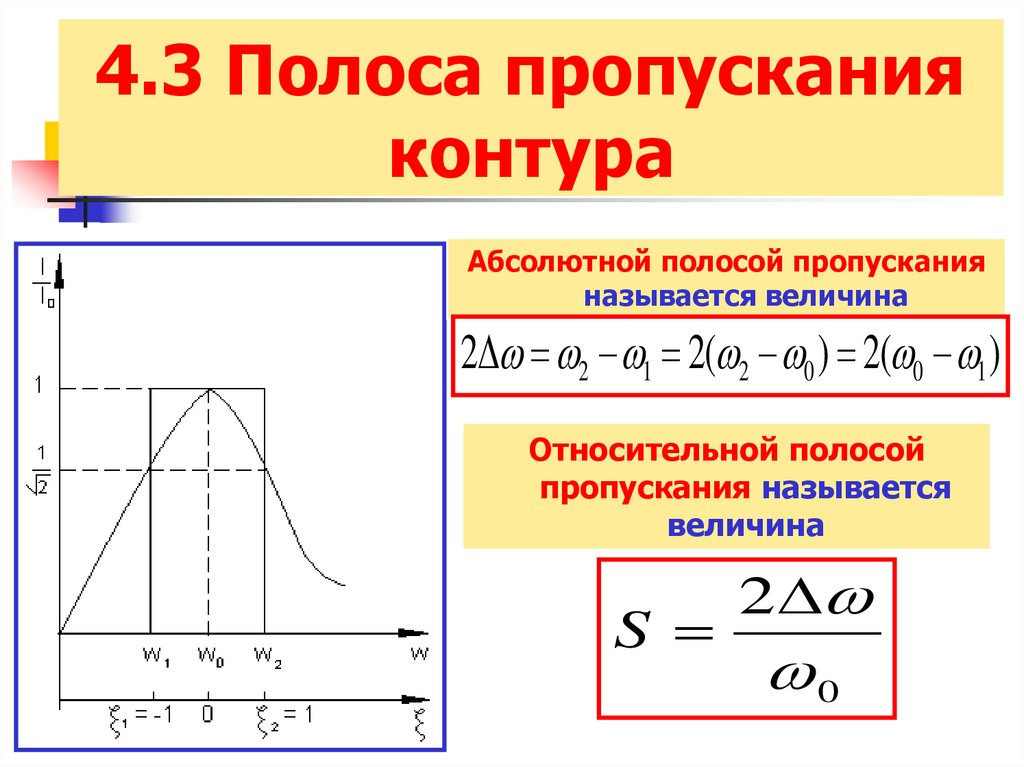
31. 4.3 Полоса пропускания контура
Абсолютной полосой пропусканияназывается величина
2 2 1 2( 2 0 ) 2( 0 1 )
Относительной полосой
пропускания называется
величина
S
2
0
32. Граничная частота – это та частота, при которой средняя мощность, поглощаемая последовательным контуром, вдвое меньше средней
мощности,поглощаемой при резонансе:
P
I 2R
1
2
P0
I0 R
2
I
1
1
2
I0
2
1
0
1, 2 1 ( )Q
0
Полоса пропускания
последовательного
колебательного контура – это
диапазон частот, в пределах
которого значения АЧХ
составляют не менее , чем
ее максимального значения на
резонансной частоте
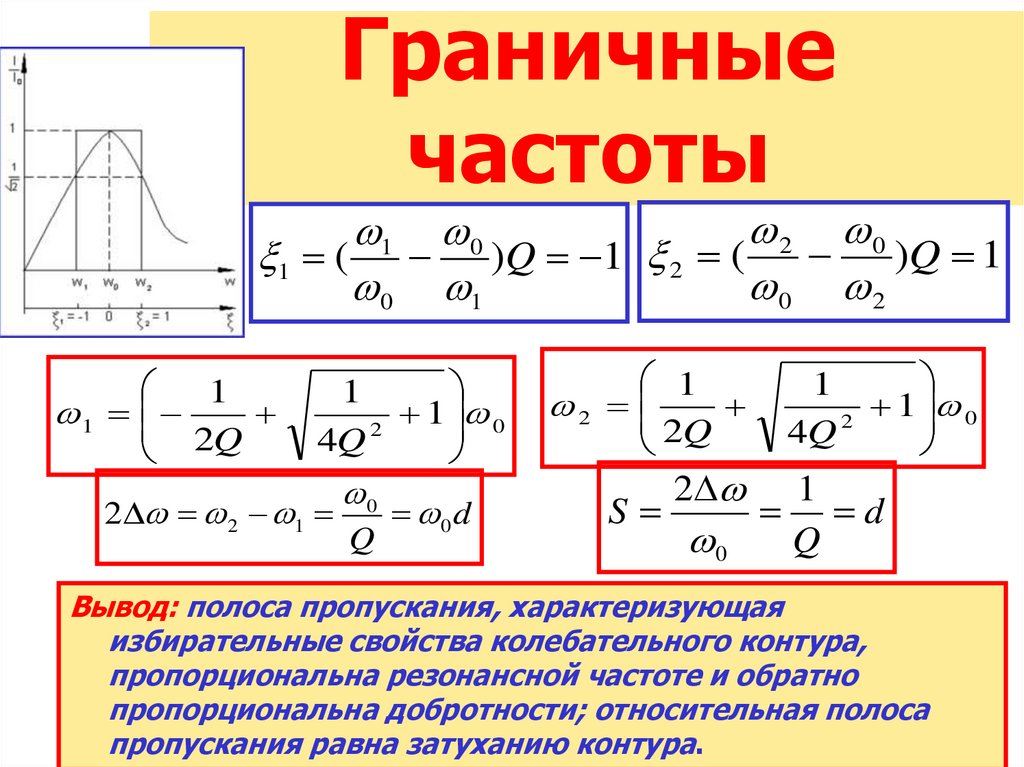
33. Граничные частоты
2 01 0
1 ( )Q 1 2 ( )Q 1
0 2
0 1
1
1
2Q
1
1 0
2
4Q
2 2 1
0
Q
0 d
1
2
2Q
S
2
0
1
1 0
2
4Q
1
d
Q
Вывод: полоса пропускания, характеризующая
избирательные свойства колебательного контура,
пропорциональна резонансной частоте и обратно
пропорциональна добротности; относительная полоса
пропускания равна затуханию контура.
34.
Добротность контура Qхарактеризует «избирательные»
свойства резонансного контура, в
частности, его полосу пропускания:
34
35.
IIр
Q2 > Q1
Q1
0,707Iр
Q2
ω
2∆ω2
ωp
2∆ω1
35































 Физика
Физика








