Геометрический смысл производной

2.

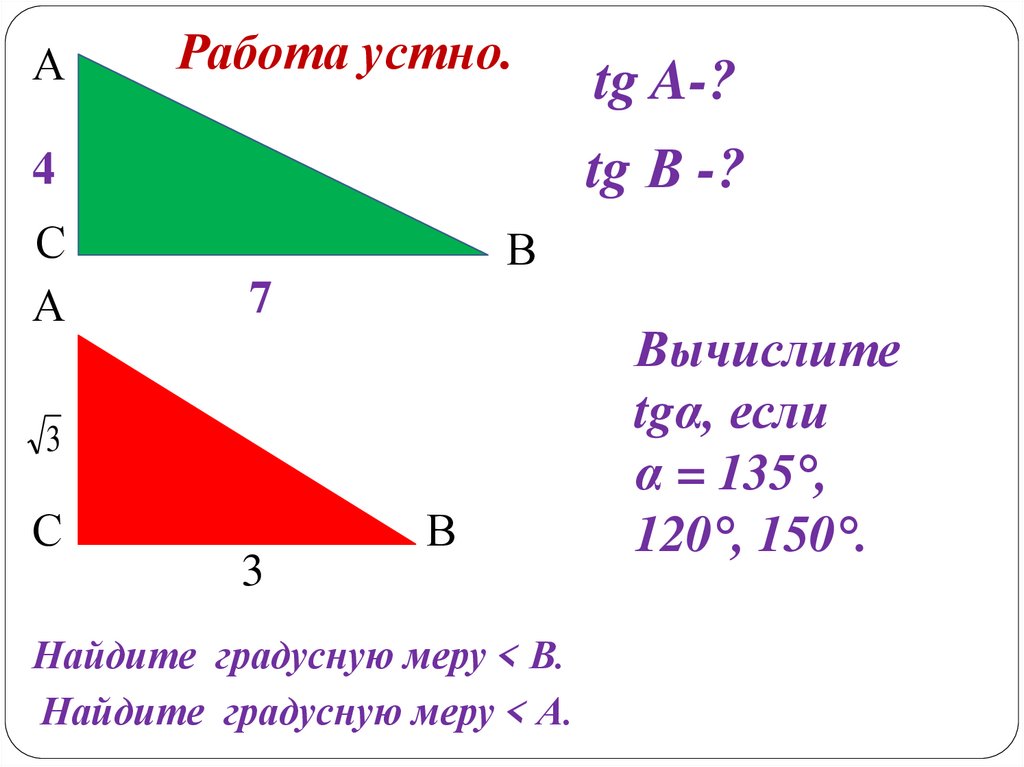
А
Работа устно.
tg В -?
4
С
А
В
7
3
С
tg A-?
3
В
Найдите градусную меру < В.
Найдите градусную меру < А.
Вычислите
tgα, если
α = 135°,
120°, 150°.

Острый или тупой угол образует
касательная к графику функции в точке
х₀ с положительной полуосью Ох?
y 2 x , x0 1
2
y ( x 5) , x0 3
3
2
y x x , x0 1
2
Чему равен тангенс угла наклона
касательной к графику функции y = x² + 2
в точке х₀ = -1?

4.

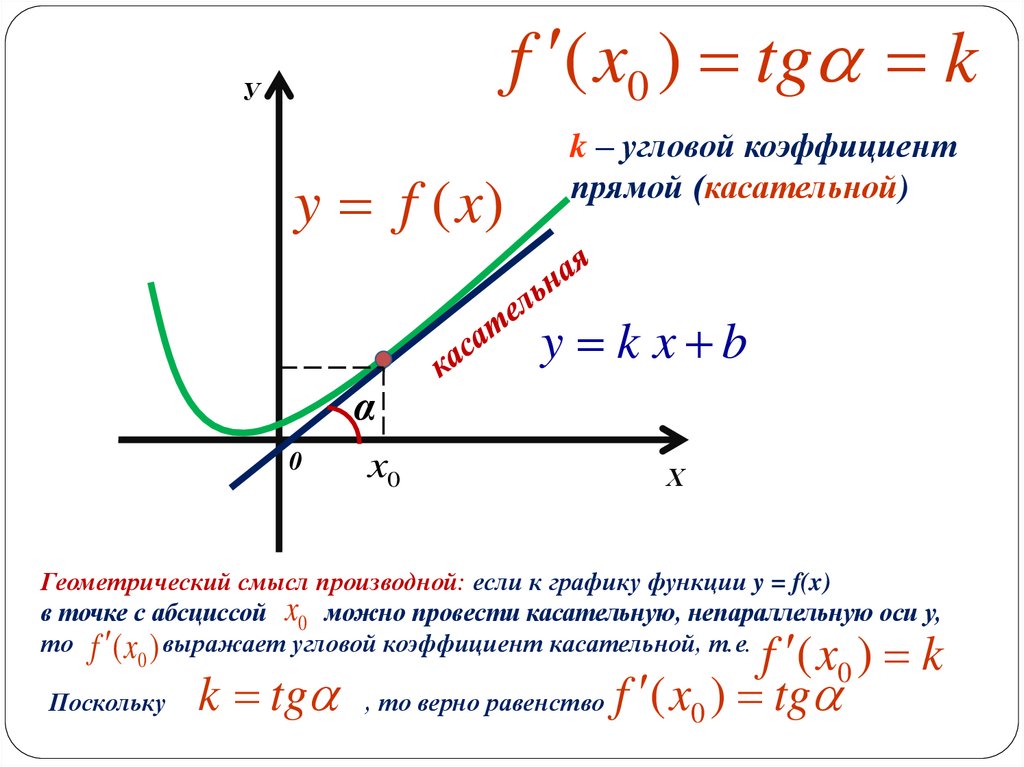
f ( x0 ) tg k
У
y f (x)
k – угловой коэффициент
прямой (касательной)
y k x b
α
0
x0
Х
Геометрический смысл производной: если к графику функции y = f(x)
в точке с абсциссой x0 можно провести касательную, непараллельную оси у,
то f ( x ) выражает угловой коэффициент касательной, т.е.
f ( x0 ) k
Поскольку k tg , то верно равенство f ( x0 ) tg
0

5.

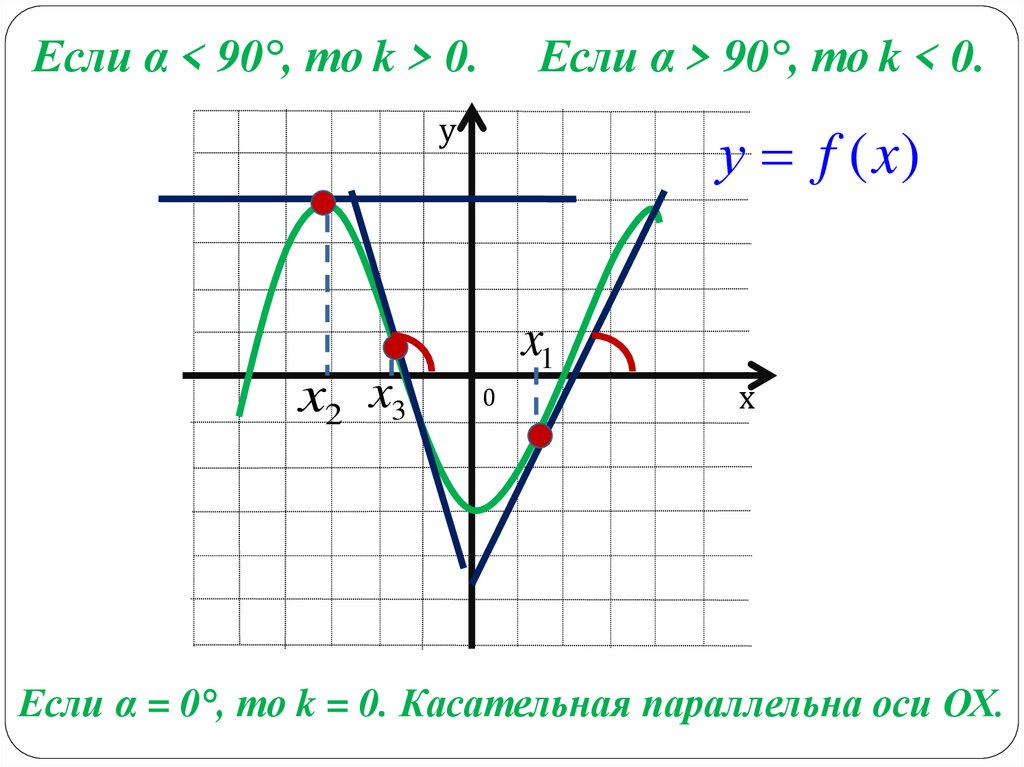
Если α < 90°, то k > 0.
Если α > 90°, то k < 0.
у
x2 x3
у f (x)
x1
0
х
Если α = 0°, то k = 0. Касательная параллельна оси ОХ.

6.

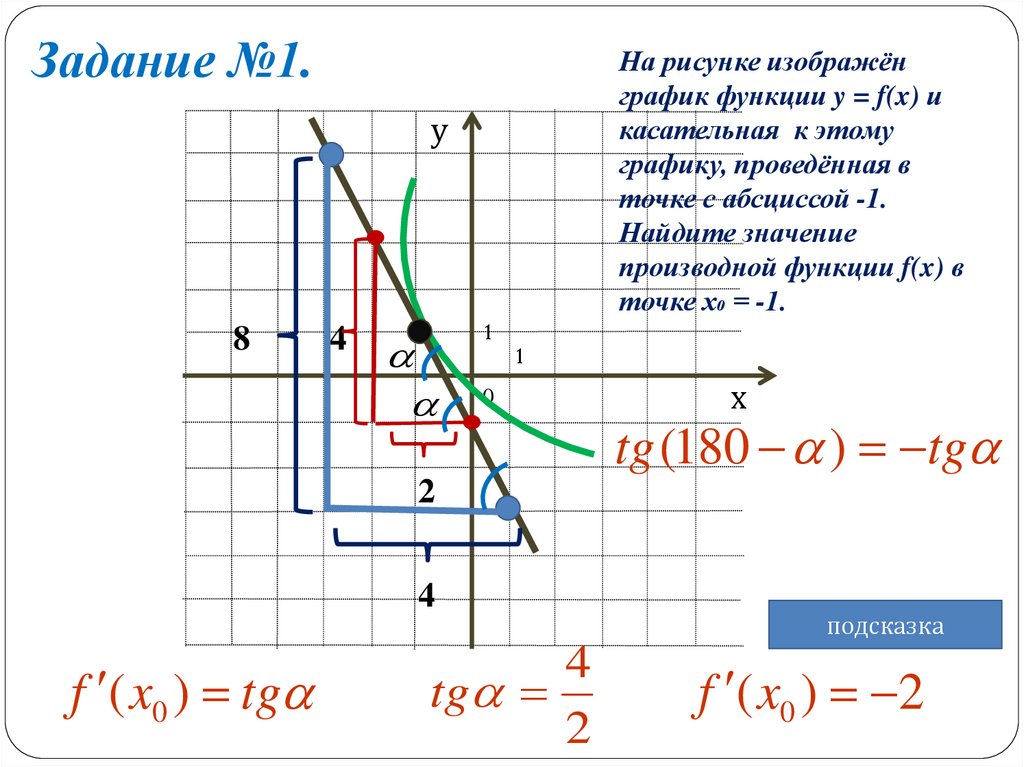
Задание №1.
На рисунке изображён
график функции y = f(x) и
касательная к этому
графику, проведённая в
точке с абсциссой -1.
Найдите значение
производной функции f(x) в
точке х₀ = -1.
у
8
4
1
1
0
х
tg (180 ) tg
2
4
f ( x0 ) tg
4
tg
2
подсказка
f ( x0 ) 2

7.

Задание №2.
6
Ответ:
8
В8 0
,
7
5

8.

Задание №3.
Ответ:
В8
-
3

9.

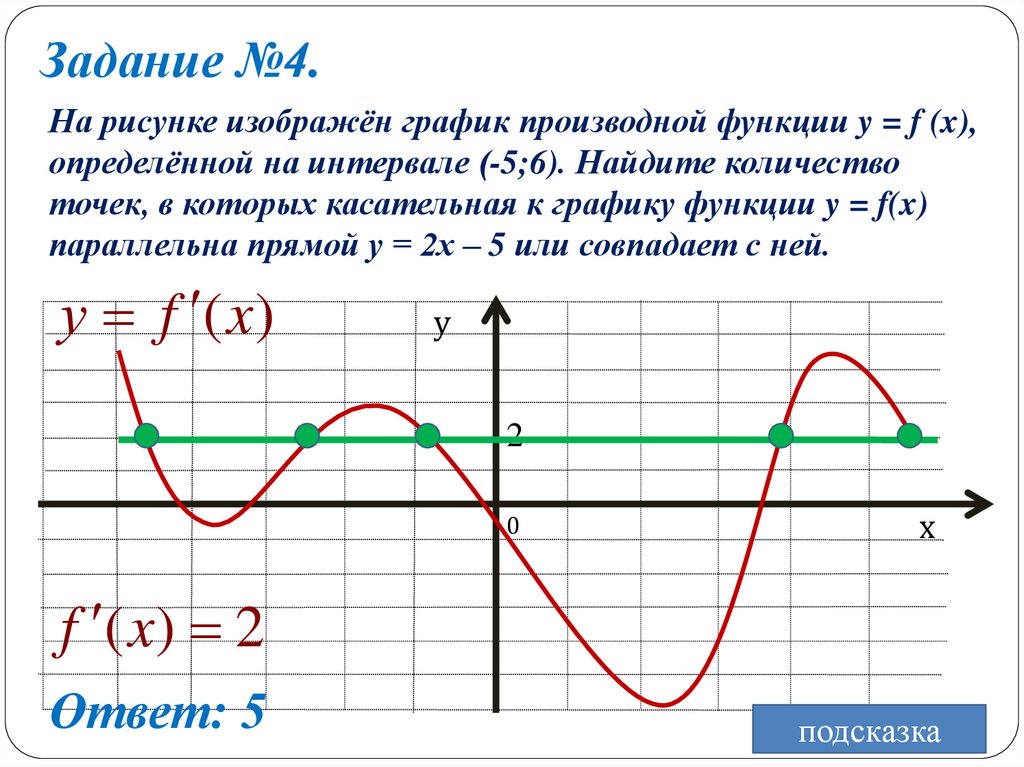
Задание №4.
На рисунке изображён график производной функции y = f (x),
определённой на интервале (-5;6). Найдите количество
точек, в которых касательная к графику функции y = f(x)
параллельна прямой у = 2х – 5 или совпадает с ней.
у f (x)
у
2
0
х
f ( x) 2
Ответ: 5
подсказка

Геометрический смысл производной

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.