Похожие презентации:
Лінії другого порядку. Гіпербола. Парабола
1.
Тема: Лінії другого порядку. Гіпербола.Парабола.
2.
1. Гіпербола.Гіперболою називається множина всіх точок площини,
модуль різниці відстаней яких від двох заданих точок
цієї площини, які називаються фокусами, є величина
стала і менша відстані між фокусами.
3.
Позначимо через F1 і F2 фокуси гіперболи, відстань міжними – 2с, а модуль різниці відстаней від довільної
точки гіперболи до фокусів – 2а. За означенням а ˂ с.
Щоб вивести рівняння гіперболи виберемо на площині
прямокутну систему координат так, щоб вісь Ох
проходила через фокуси, а початок координат поділив
відрізок F1F2 навпіл.
4.
Точка М(х, у) площини лежить на гіперболі тоді і тількитоді, коли ||МF1| – |MF2||=2а, або
( x c)2 y 2 ( x c)2 y 2 2а
5.
Після проведення таких же перетворень, як прививеденні рівняння еліпса, отримаємо канонічне
рівняння гіперболи
2
де
2
x
y
2 1
2
a
b
(1)
b2 = c2 – a2
(2)
6.
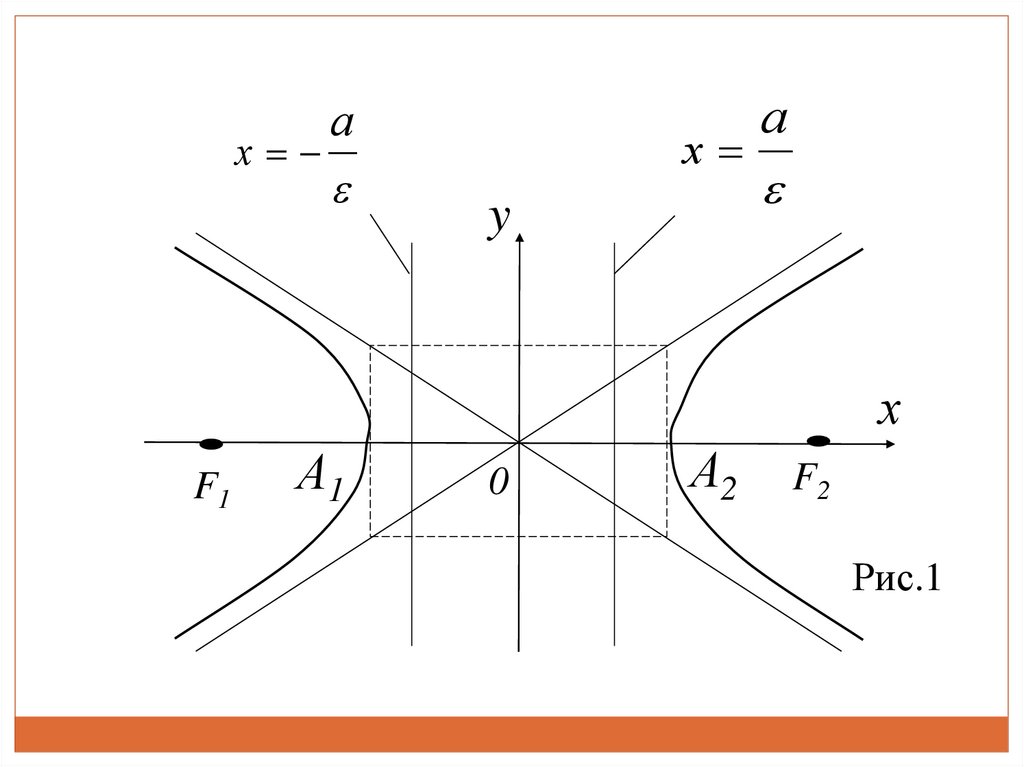
xa
x
y
a
х
F1
А1
0
А2
F2
Рис.1
7.
Встановимо деякі властивості і дослідимо формугіперболи.
1.
Гіпербола
розташована
симетрично
відносно
координатних осей і початку координат. Осі симетрії
називаються осями гіперболи, а точка перетину осей –
її центром.
8.
2. Знайдемо точки перетину гіперболи з осямикоординат. Із (1): коли у = 0 то х = ± а, тобто маємо дві
точки перетину з віссю Ох: А1(–а, 0); А2(а, 0);
коли х = 0 то у2 = – b2, отже перетину з віссю Оу
гіпербола немає.
Але точки B1(0, – b); B2(0, b) також розглядаються.
Точки А1(– а, 0); А2(а, 0) – вершини гіперболи.
9.
Відрізок А1А2, який сполучає вершини гіперболи,довжина якого дорівнює 2а, називається дійсною віссю
гіперболи, відрізок В1В2, довжина якого 2b, який не має
спільних точок з гіперболою, називається уявною
віссю. Числа а та b називаються відповідно дійсною і
уявною піввіссю.
10.
Відрізок F1F2 довжиною 2с – фокальна вісь гіперболи,с – фокальна піввісь. Фокуси F1 і F2 розташовані на
тій же прямій, що і дійсна вісь.
Прямокутник із сторонами 2а і 2b називається
основним прямокутником гіперболи.
11.
3. Пряма називається асимптотою кривої, якщовідстань від змінної точки М(х, у) кривої до цієї прямої
прямує до нуля, якщо точка, рухаючись по кривій,
віддаляється у нескінченність.
12.
Для гіперболи, заданої рівнянням (1), асимптотами єпрямі, які проходять через початок координат і
співпадають з діагоналями основного прямокутника.
Гіпербола складається з двох віток і має дві асимптоти:
b
y x,
a
b
y x
a
(3)
13.
При побудові гіперболи (1) доцільно спочаткупобудувати основний прямокутник, провести прямі, що
проходять
через
протилежні
вершини
прямокутника – асимптоти гіперболи
і
вершини А1(–а, 0); А2(а, 0) гіперболи (рис. 1).
цього
визначити
14.
Гіпербола з рівними півосями а = b називаєтьсярівносторонньою, її канонічне рівняння має вигляд
x2 y2 a2
(4)
Основним прямокутником рівносторонньої гіперболи є
квадрат зі стороною 2а, а її асимптотами – бісектриси
координатних кутів.
15.
Рівняння2
2
y
x
1
b2 a2
(5)
також визначає гіперболу. При цьому вершини цієї
гіперболи лежать в точках B1(0, – b); B2(0, b)на осі Оу, а
її асимптоти збігаються з асимптотами гіперболи (1)
рис. 2.
16.
yF2
B2
A1
о
B1
F1
A2
x
17.
Якщо у гіперболах2
2
x
y
2 1,
2
a
b
2
2
x
y
2 2 1
a
b
числа а та b одні і ті ж самі, то гіперболи називаються
спряженими.
18.
4. Ексцентриситет гіперболи визначається яквідношення половини фокальної відстані до довжини її
дійсної півосі:
c
a
(6)
Оскільки с > а, то 1 . З формул (2) та (6) маємо:
c
a
a b
b
1 2
a
a
2
2
2
19.
Отже, ексцентриситет характеризує форму гіперболи:чим більший ексцентриситет, тим більше відношення
b
a , тобто тим більше основний прямокутник
розтягується в напрямі осі Оу, а гіпербола відхиляється
від осі Ох. Чим ближче ексцентриситет до одиниці, тим
більше основний прямокутник розтягується в напрямі
осі Ох, а гіпербола наближається до неї.
20.
5. Директрисами гіперболи називаються дві прямі,перпендикулярні до дійсної осі гіперболи і
розташовані симетрично відносно центра на віддалі
від нього.
a
21.
Якщо гіпербола задана канонічним рівнянням, то їїдиректрисами будуть прямі
a
x
x
a
(7)
22.
6. Фокальною хордою гіперболи називається хорда,що проходить через фокус перпендикулярно до дійсної
осі.
2р – довжина цієї хорди, число р – фокальна півхорда.
2
b
p
a
(8)
23.
Якщо центр гіперболи знаходиться у точці С(х0, у0),то рівняння гіперболи має такий вигляд:
x x 0 2
a
2
y y 0 2
b
2
1
(9)
24.
2. Парабола.Параболою називається множина всіх точок площини,
кожна з яких рівновіддалена від даної точки, яка
називається фокусом, і від даної прямої, яка
називається директрисою (за умови, що директриса не
проходить через фокус).
25.
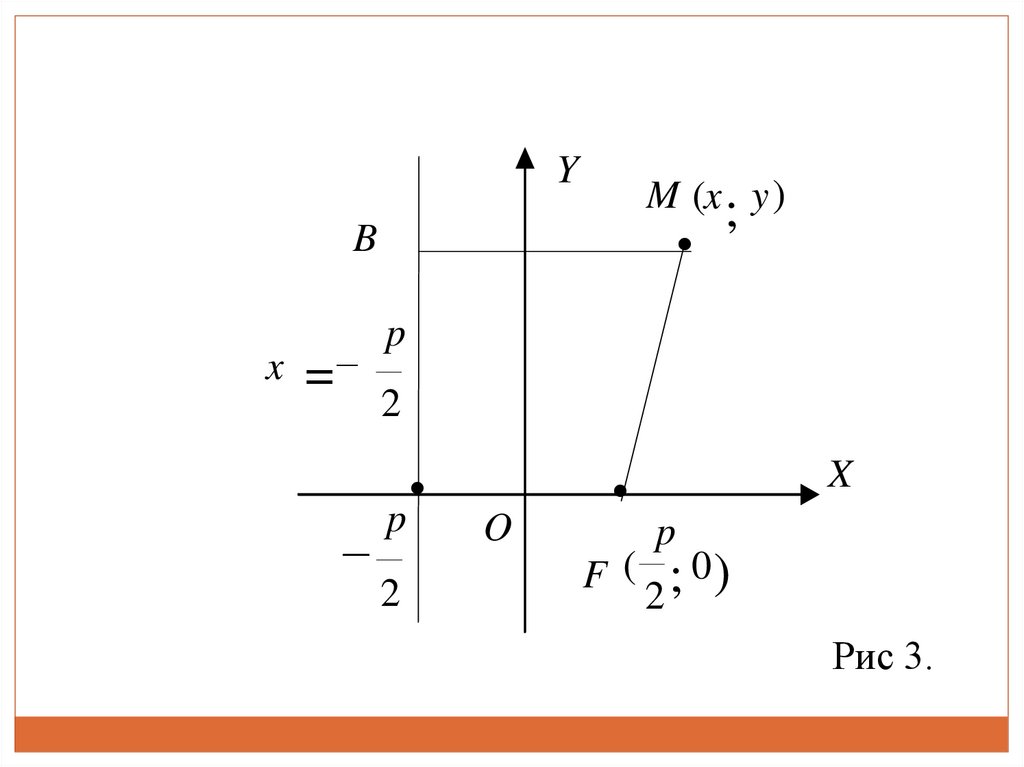
Виведемо рівняння параболи. Нехай на площині заданіфокус F і директриса, причому відстань від фокуса
до директриси дорівнює p. Виберемо систему
координат так, щоб вісь Ох проходила через фокус F,
перпендикулярно до директриси, а початок координат
ділив навпіл відстань між фокусом і директрисою
(рис. 3).
26.
YM (x ; y )
B
x =−
−
p
2
p
2
O
F (
X
p
0)
;
2
Рис 3.
27.
Тоді фокус має координати F p ;0 , а рівняння2
p
директриси має вигляд x
2
Нехай М(х, у) − довільна точка площини, а відрізки MB
і MF − відстані від точки М(х, у) до директриси і
фокуса відповідно, координати точки В p ; y
2
28.
Точка M буде належати параболі тоді і тільки тоді,коли MB = MF або
2
p
p
2
x y x
2
2
(10)
Це і є рівняння параболи, записане за її означенням.
29.
Щоб спростити його, піднесемо обидві частинирівності (10) до квадрата:
2
2
p
p
2
2
x px
y x px
,
4
4
2
тобто
y 2 px
2
(11)
Рівняння (11) називається канонічним рівнянням
параболи.
30.
Встановимо деякі властивості і дослідимо формупараболи.
Парабола має одну вісь симетрії і не має центра
симетрії. Вісь симетрії для рівняння (11) співпадає з
віссю Ох.
Значення x = 0, y = 0 задовольняють рівняння (11),
тобто парабола проходить через початок координат
(рис.4)
31.
32.
y 2 px2
(рис.4)
координати фокуса
p
F ,0
2
рівняння директриси
p
x
2
33.
Точкаперетину
параболи
з
її
віссю
симетрії
називається вершиною параболи; число, яке дорівнює
відстані від фокуса до директриси – параметром
параболи. Параметр p характеризує ширину області,
яку обмежує парабола.
34.
Фокальною хордою параболи називається хорда, щопроходить через фокус F, перпендикулярно до осі
симетрії. Довжина фокальної хорди дорівнює 2р.
Ексцентриситет параболи за означенням покладають
рівним 1.
35.
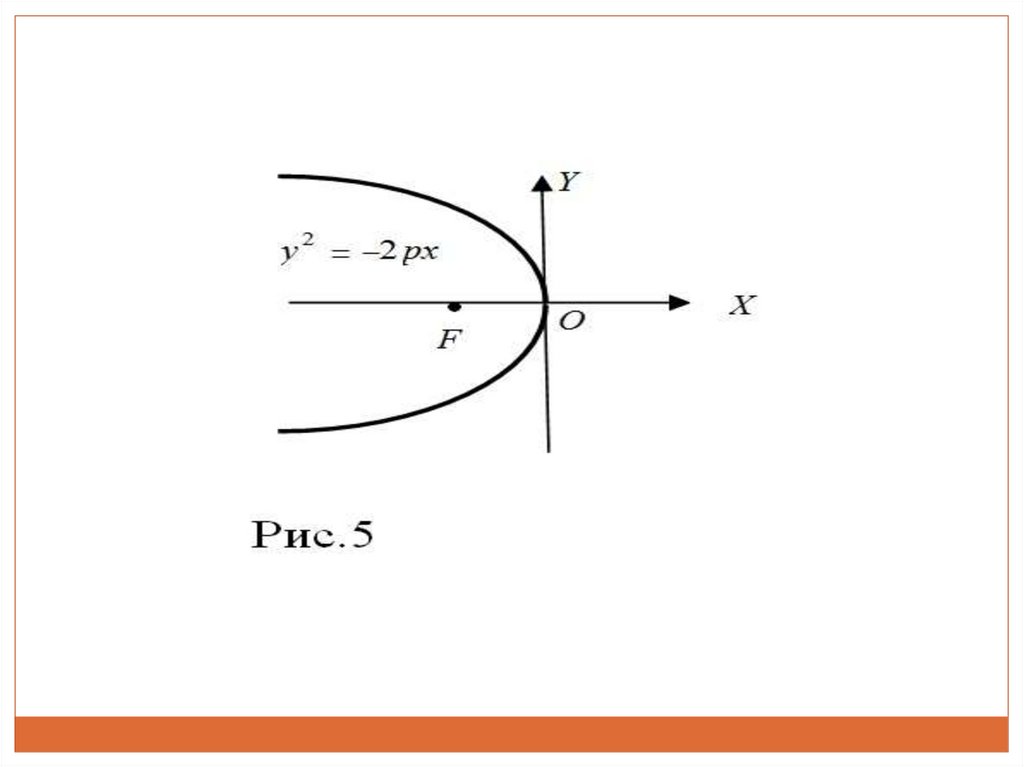
y 2 px, p 02
(рис.5)
координати фокуса
p
F ,0
2
рівняння директриси
p
x
2
36.
37.
х 2 pу2
(рис.6)
визначає параболу, але з віссю симетрії, що співпадає
з віссю Оу
координати фокуса
p
F 0,
2
рівняння директриси
p
y
2
38.
39.
х 2 pу, p 02
(рис.7)
координати фокуса
p
F 0;
2
рівняння директриси
p
y
2
40.
YO
X
F
2
= − 2 ру
Рис.7
x
41.
Якщо вершина параболи знаходиться у точці С(х0, у0),то її рівняння має такий вигляд:
х х0 2 p у у0
2
у у0 2 p х х0
2
42.
3. Побудова ліній другого порядку за їх рівняннями.Методом виділення повного квадрата рівняння другого
степеня Ax2 + Cy2 + 2Dx + 2Ey+F=0 зводиться до
канонічного рівняння кривої другого порядку, при
цьому, якщо:
1. АС > 0, маємо рівняння еліпса
(А = С − рівняння кола)
2. АС < 0, маємо рівняння гіперболи
3. АС = 0, маємо рівняння параболи.







































 Математика
Математика








