Похожие презентации:
Пряма на площині (лекція 6)
1. § 3. ПРЯМА НА ПЛОЩИНІ
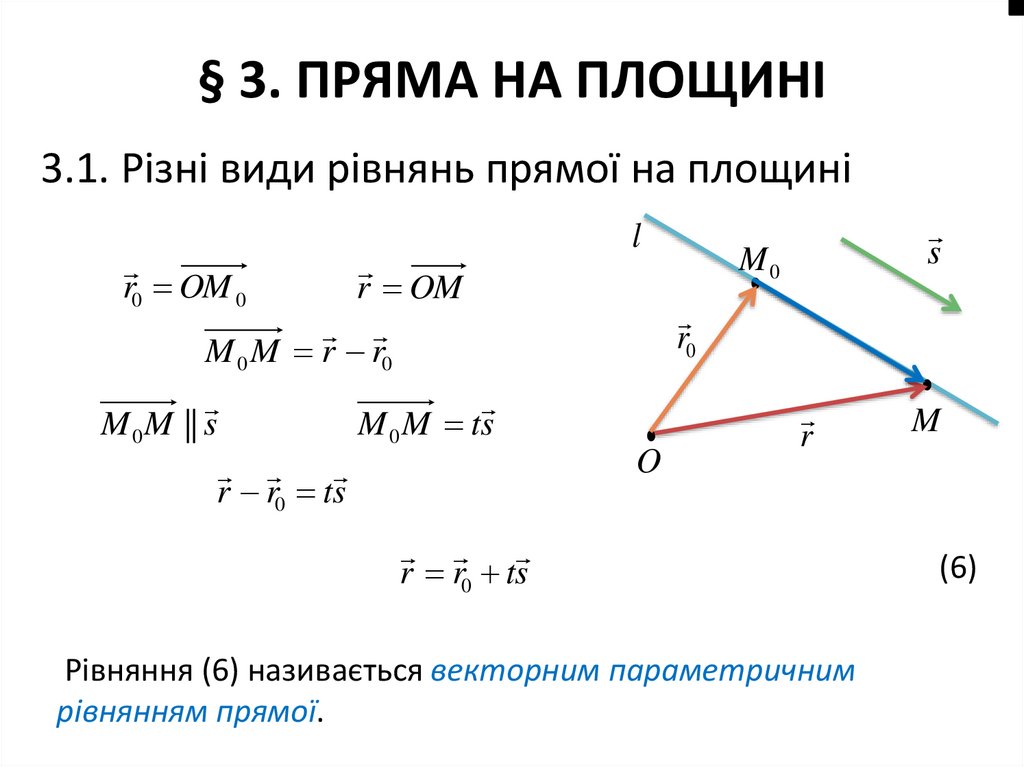
3.1. Різні види рівнянь прямої на площиніr0 OM 0
r OM
M 0 M r r0
M 0 M || s
M 0 M ts
r r0 ts
l
s
M0
r0
O
r
r r0 ts
Рівняння (6) називається векторним параметричним
рівнянням прямої.
M
(6)
2.
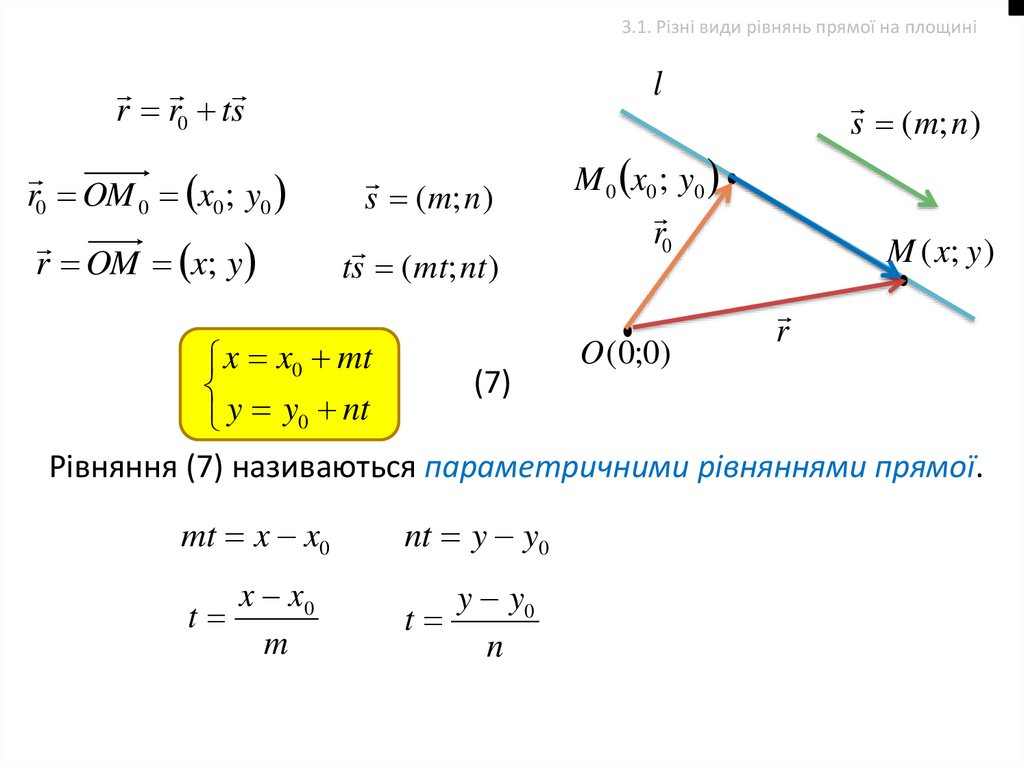
3.1. Різні види рівнянь прямої на площиніl
r r0 ts
r0 OM 0 x0 ; y0
r OM x; y
s ( m; n )
ts ( mt; nt )
s ( m; n )
M 0 x0 ; y0
r0
M ( x; y )
r
O ( 0;0)
x x0 mt
(7)
y y0 nt
Рівняння (7) називаються параметричними рівняннями прямої.
mt x x0
nt y y0
x x0
t
m
y y0
t
n
3.
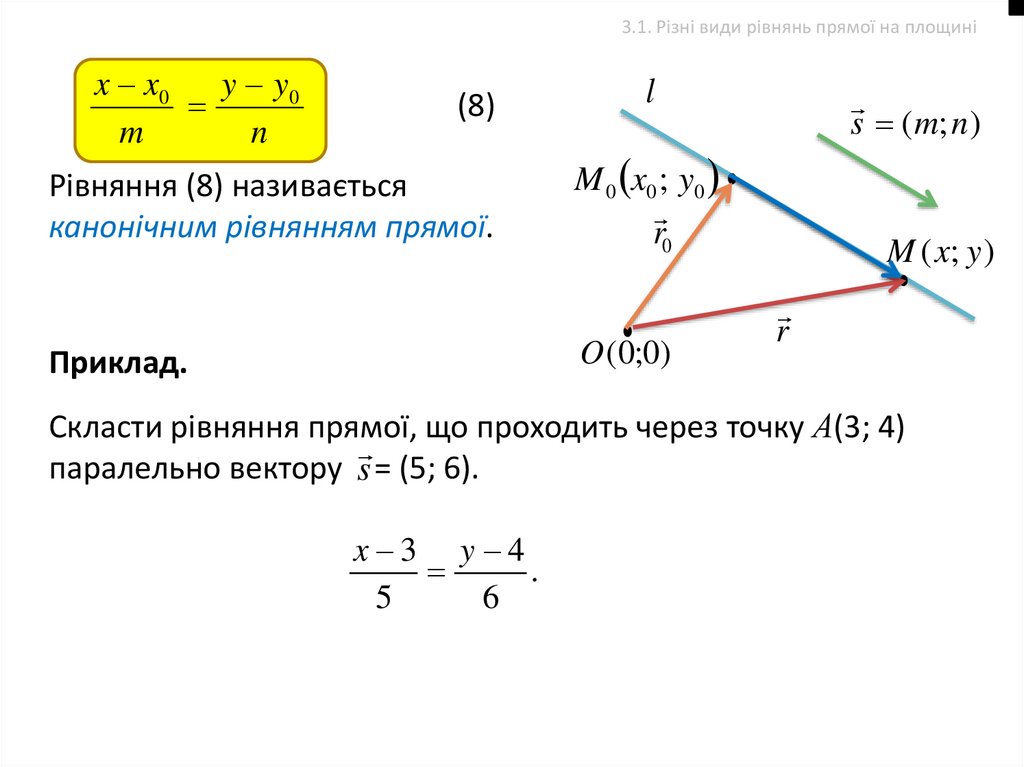
3.1. Різні види рівнянь прямої на площиніx x0
y y0
m
n
(8)
Рівняння (8) називається
канонічним рівнянням прямої.
l
M 0 x0 ; y0
r0
O ( 0;0)
Приклад.
s ( m; n )
M ( x; y )
r
Скласти рівняння прямої, що проходить через точку А(3; 4)
паралельно вектору s = (5; 6).
x 3 y 4
.
5
6
4.
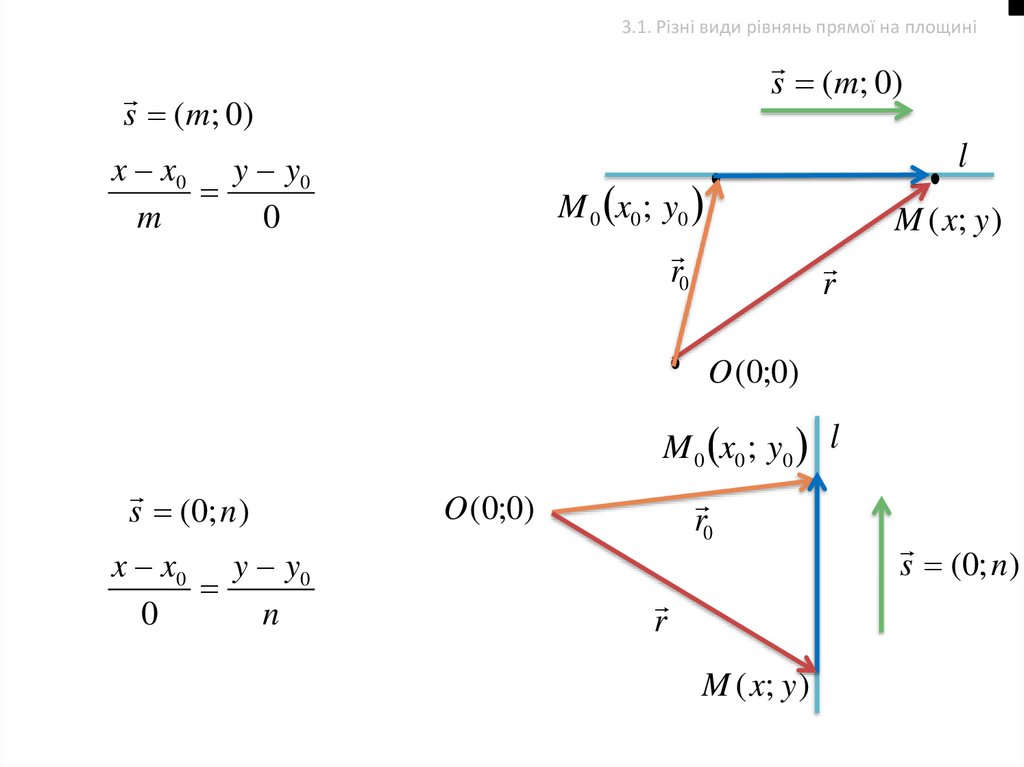
3.1. Різні види рівнянь прямої на площиніs (m; 0)
s (m; 0)
x x0 y y0
m
0
l
M 0 x0 ; y0
r0
M ( x; y )
r
O ( 0;0)
s (0; n )
x x0 y y0
0
n
O ( 0;0)
M 0 x0 ; y0 l
r0
r
M ( x; y )
s (0; n )
5.
3.1. Різні види рівнянь прямої на площиніx x0 y y0
m
n
y y0 x x0
n
m
n
y y 0 x x0
m
y y0 k x x0
m 0
k
y
y0
(8)
M0
b
m
0
s ( m; n )
x0
(9)
n
tg
m
Рівняння (9) називається рівнянням прямої, яка проходить
через задану точку і має заданий кутовий коефіцієнт.
n
x
6.
3.1. Різні види рівнянь прямої на площиніy
y y0 k x x0
(9)
y kx b
(10)
Рівняння (10) називається
рівнянням прямої
з кутовим коефіцієнтом.
b
0
x
y
y kx
(11)
Рівняння (11) називається
рівнянням прямої
пропорційності.
0
x
7.
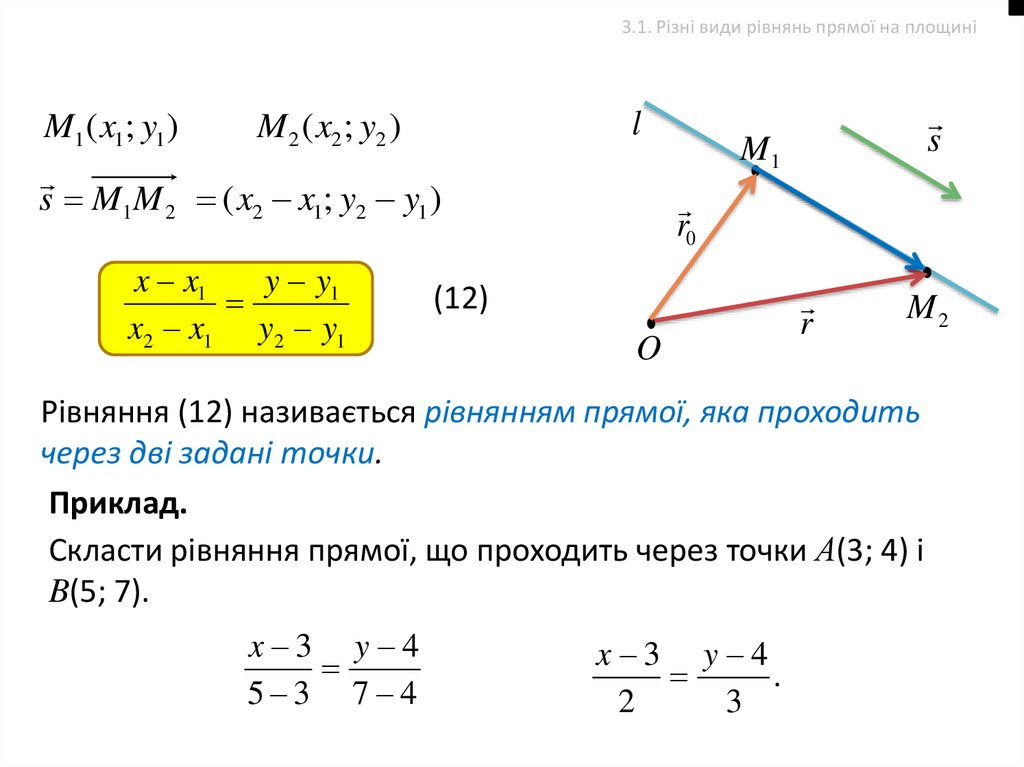
3.1. Різні види рівнянь прямої на площиніM1 ( x1; y1 )
M 2 ( x2 ; y2 )
s M1M 2 ( x2 x1; y2 y1 )
x x1
y y1
x2 x1 y2 y1
l
s
M1
r0
(12)
O
r
M2
Рівняння (12) називається рівнянням прямої, яка проходить
через дві задані точки.
Приклад.
Скласти рівняння прямої, що проходить через точки А(3; 4) і
B(5; 7).
x 3 y 4
5 3 7 4
x 3 y 4
.
2
3
8.
3.1. Різні види рівнянь прямої на площиніA(a;0)
x a y 0
0 a b 0
x y
1
a b
B (0; b)
x a y
a
b
x
a y
a a b
(13)
B (0; b)
b
A(a;0)
a
Рівняння (13) називається рівнянням прямої у відрізках на осях.
Приклад.
Скласти рівняння прямої, що проходить через точки А(3; 0) і
B(0; 4).
x y
1.
3 4
9.
3.1. Різні види рівнянь прямої на площиніl n
M ( x; y ) l
M1 ( x1; y1 ) l
n ( A, B )
y
n
M ( x; y )
M1M ( x x1; y y1 )
M1M n
M1 M n 0
A( x x1 ) B( y y1 ) 0
l
x
0
M1 ( x1; y1 )
(14)
Рівняння (14) називається рівнянням прямої, яка проходить
через задану точку перпендикулярно до заданого вектора.
Вектор n ( A, B ) називається нормальним вектором прямої.
10.
3.2. Загальне рівняння прямої та йогодослідження
A( x x1 ) B( y y1 ) 0
Ax By C 0
(15)
Рівняння (15) називається загальним рівнянням прямої.
Α=0
n (0; B )
l || Ox
B=0
n ( A;0)
l || Oy
11.
3.3. Кут між двома прямими. Умови паралельностіі перпендикулярності двох прямих
x x1 y y1
m1
n1
s1 (m1; n1 )
l1 :
l2 :
s2 (m2 ; n2 )
l1 ,l2 s1 , s2
m1m2 n1n2
s1 s2
cos
s1 s2
m12 n12 m22 n22
l1 || l2
m1 n1
m2 n2
x x2 y y 2
m2
n2
l1 l2
0
2
(18)
m1m2 n1n2 0
12.
3.3. Кут між двома прямими. Умови паралельності і перпендикулярності двох прямихA1x B1 y C1 0
n1 ( A1; B1 )
l1 :
A2 x B2 y C2 0
n2 ( A2 ; B2 )
l2 :
0
2
l1 ,l2 n1 , n2
n1 n2
cos
n1 n2
l1 || l2
A1 B1
A2 B2
A1 A2 B1B2
A B A B
(21)
l1 l2
A1 A2 B1B2 0
2
1
2
1
2
2
2
2
13.
3.3. Кут між двома прямими. Умови паралельності і перпендикулярності двох прямихl1 :
A1x B1 y C1 0
A1 x B1 y C1
A12 B12
l2 :
A2 x B2 y C2 0
A2 x B2 y C2
A22 B22
– бісектриси кутів між прямими.
14.
3.3. Кут між двома прямими. Умови паралельності і перпендикулярності двох прямихl1 :
y k1x b1
l2 :
y k2 x b2
k2 tg 2
k1 tg 1
l1 ,l2
k2 k1
tg
1 k1k2
tg 2 tg 1
tg tg( 1 2 )
1 tg 1 tg 2
l1 || l2
k1 k2
l1 l2
0
2
2
k2
(24)
1
2
k1
15.
3.4. Відстань від точки до прямоїl:
Ax By C 0
a b
прb a .
b
16.
3.4. Відстань від точки до прямоїl:
Ax By C 0
n M 1M 0
d прn M1M 0
n
d
M 0 ( x0 ; y0 )
n
d
l
Ax0 By 0 C
A2 B 2
Ax0 By 0 C
A2 B 2
M1 ( x1; y1 )
0
0
M 0 x0 ; y0
M 0 x0 ; y0
O 0; 0
O 0; 0
17. § 4. ПЛОЩИНА В ПРОСТОРІ
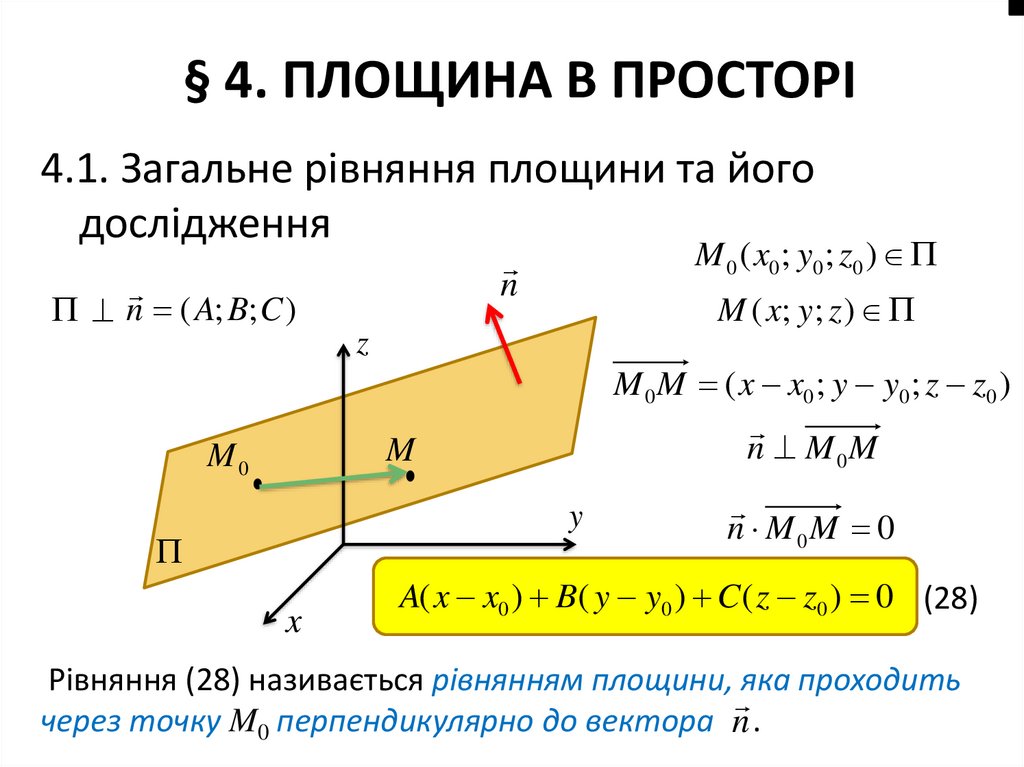
4.1. Загальне рівняння площини та йогодослідження
M 0 ( x0 ; y0 ; z0 )
n
n ( A; B; C )
M ( x; y ; z )
z
M 0 M ( x x0 ; y y0 ; z z0 )
n M 0M
M
M0
y
x
n M 0M 0
A( x x0 ) B( y y0 ) C ( z z0 ) 0 (28)
Рівняння (28) називається рівнянням площини, яка проходить
через точку M0 перпендикулярно до вектора n .
18.
4.1. Загальне рівняння площини та його дослідженняA( x x0 ) B( y y0 ) C ( z z0 ) 0
n ( A; B; C )
Ax By Cz D 0
(29)
Рівняння (29) називається загальним рівнянням площини.
Α=0
B=0
С=0
Α=B=0
Α=C=0
B=C=0
n (0; B; C )
n ( A;0; C )
n ( A; B;0)
n (0; 0; C )
n (0; B;0)
n ( A;0; 0)
|| Ox
|| Oy
|| Oz
|| Oxy
|| Oxz
|| Oyz
19.
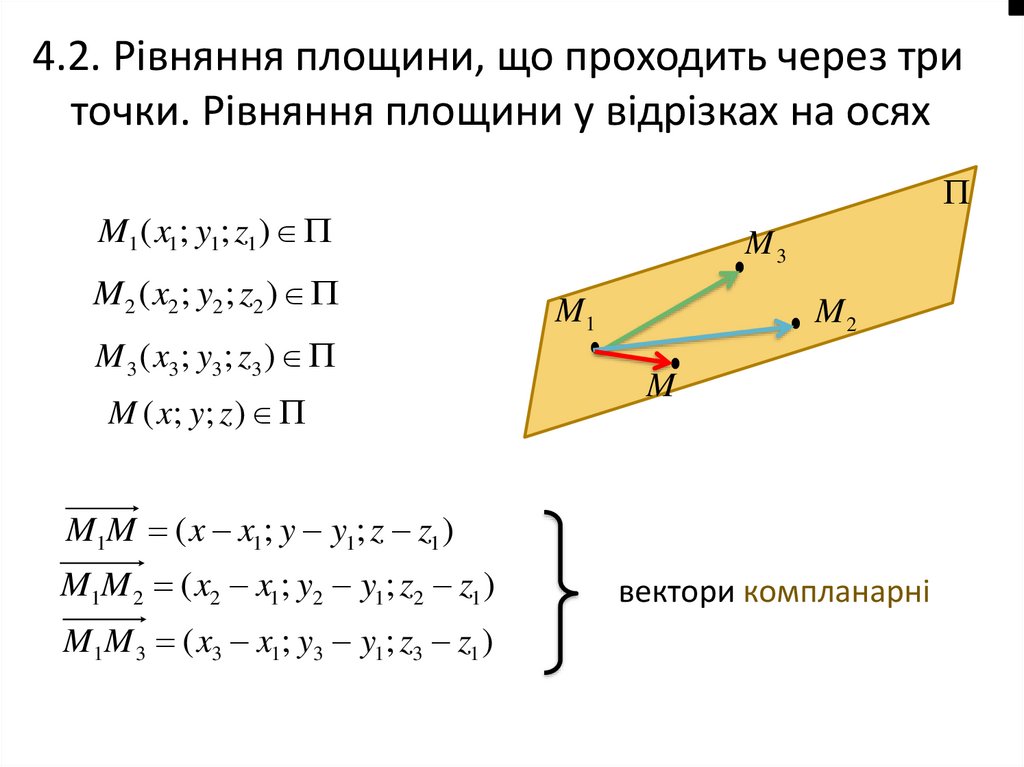
4.2. Рівняння площини, що проходить через триточки. Рівняння площини у відрізках на осях
M1 ( x1; y1; z1 )
M 2 ( x2 ; y2 ; z2 )
M 3 ( x3 ; y3 ; z3 )
M ( x; y ; z )
M3
M1
M2
M
M1M ( x x1; y y1; z z1 )
M1M 2 ( x2 x1; y2 y1; z2 z1 )
M1M 3 ( x3 x1; y3 y1; z3 z1 )
вектори компланарні
20.
4.2. Рівняння площини, що проходить через три точки. Рівняння площини у відрізках на осяхax
ab c bx
cx
ay
by
cy
az
bz
cz
M 1M M 1M 2 M 1M 3 0
x x1
x2 x1
x3 x1
вектори компланарні
y y1
y2 y1
y3 y1
z z1
z2 z1 0
z3 z1
(33)
Рівняння (33) називається рівнянням площини, що проходить
через три точки.
M1 ( x1; y1; z1 )
M 2 ( x2 ; y2 ; z2 )
M 3 ( x3 ; y3 ; z3 )
21.
4.2. Рівняння площини, що проходить через три точки. Рівняння площини у відрізках на осяхM1 ( x1; y1; z1 )
M 2 ( x2 ; y2 ; z2 )
M 3 ( x3 ; y3 ; z3 )
A(a;0;0)
B (0; b;0)
C (0;0; c )
x a y 0 z 0
0 a b 0 0 0 0
0 a 0 0 c 0
xbc yac zab abc 0
x y z
1
a b c
(34)
Рівняння (34) називається рівнянням площини у відрізках на осях.
22.
4.3. Кут між двома площинами. Умови паралельності і перпендикулярності двох площин2 : A2 x B2 y C2 z D2 0
n2 ( A2 ; B2 ; C2 )
1 : A1x B1 y C1z D1 0
n1 ( A1; B1; C1 )
0
2
n1 , n2
n1 n2
cos
n1 n2
1 || 2
A1 B1 C1
A2 B2 C2
A1 A2 B1B2 C1C2
A B C A B C
2
1
2
1
2
1
2
2
2
2
2
2
(35)
1 2 A1 A2 B1B2 C1C2 0
23.
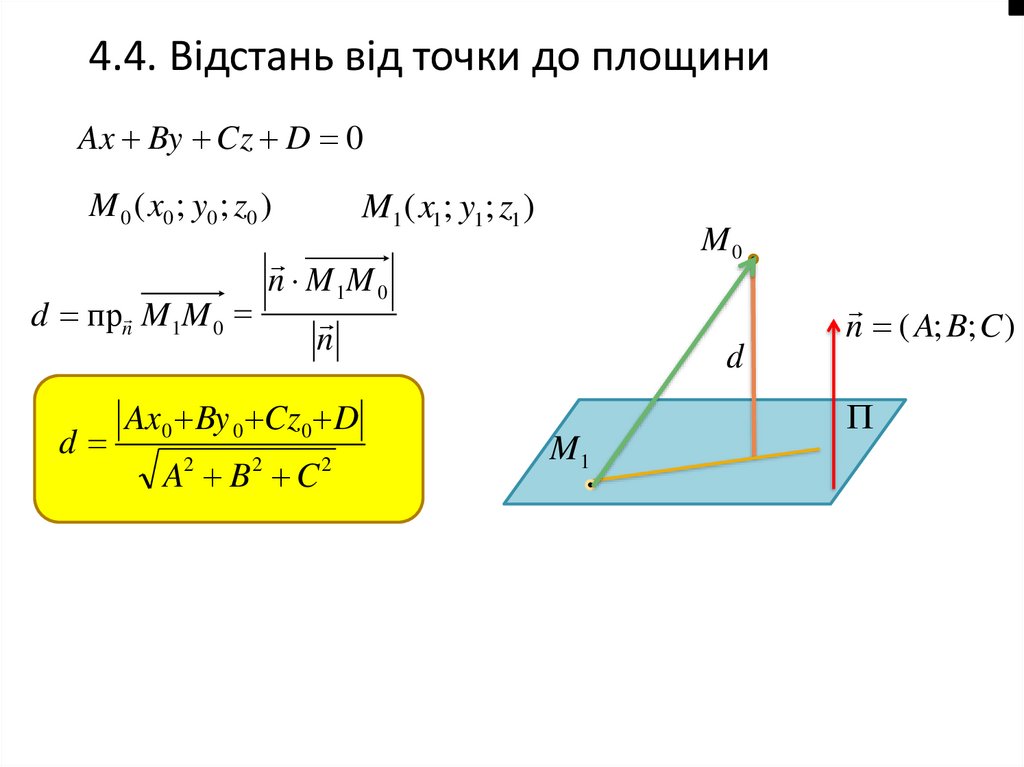
4.4. Відстань від точки до площиниAx By Cz D 0
M 0 ( x0 ; y0 ; z0 )
M1 ( x1; y1; z1 )
M0
n M 1M 0
d прn M1M 0
n
d
Ax 0 By 0 Cz0 D
A B C
2
2
2
d
M1
n ( A; B; C )
24. § 5. ПРЯМА ЛІНІЯ В ПРОСТОРІ
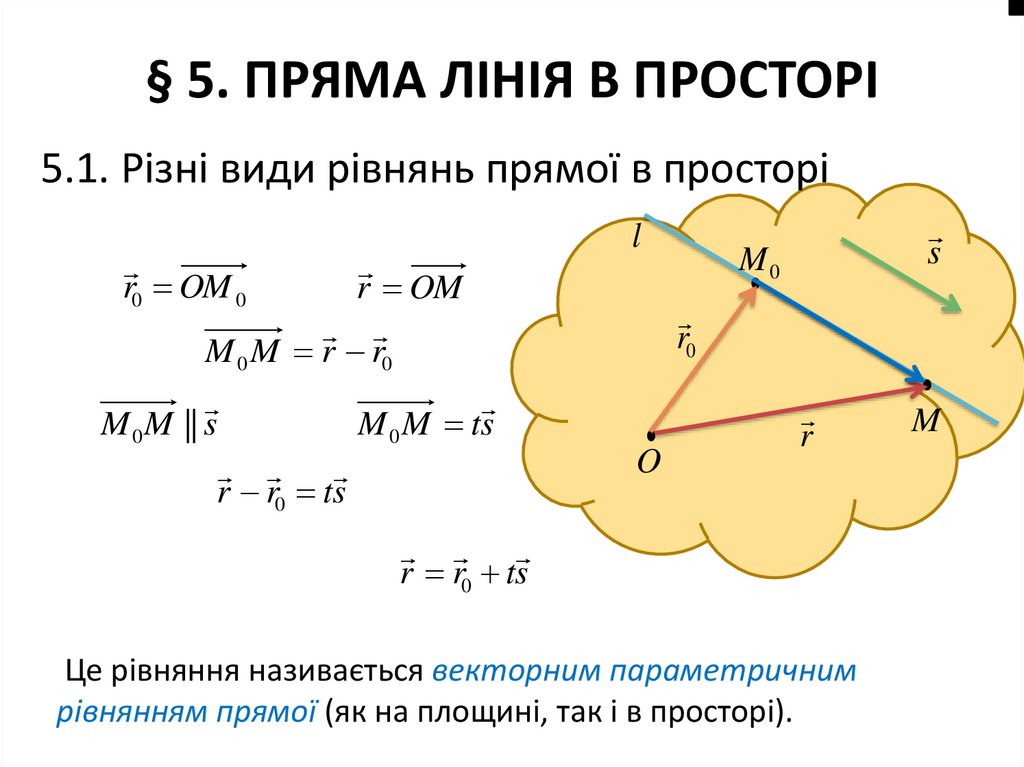
5.1. Різні види рівнянь прямої в просторіr0 OM 0
r OM
M 0 M r r0
M 0 M || s
M 0 M ts
r r0 ts
l
s
M0
r0
O
r
r r0 ts
Це рівняння називається векторним параметричним
рівнянням прямої (як на площині, так і в просторі).
M
25.
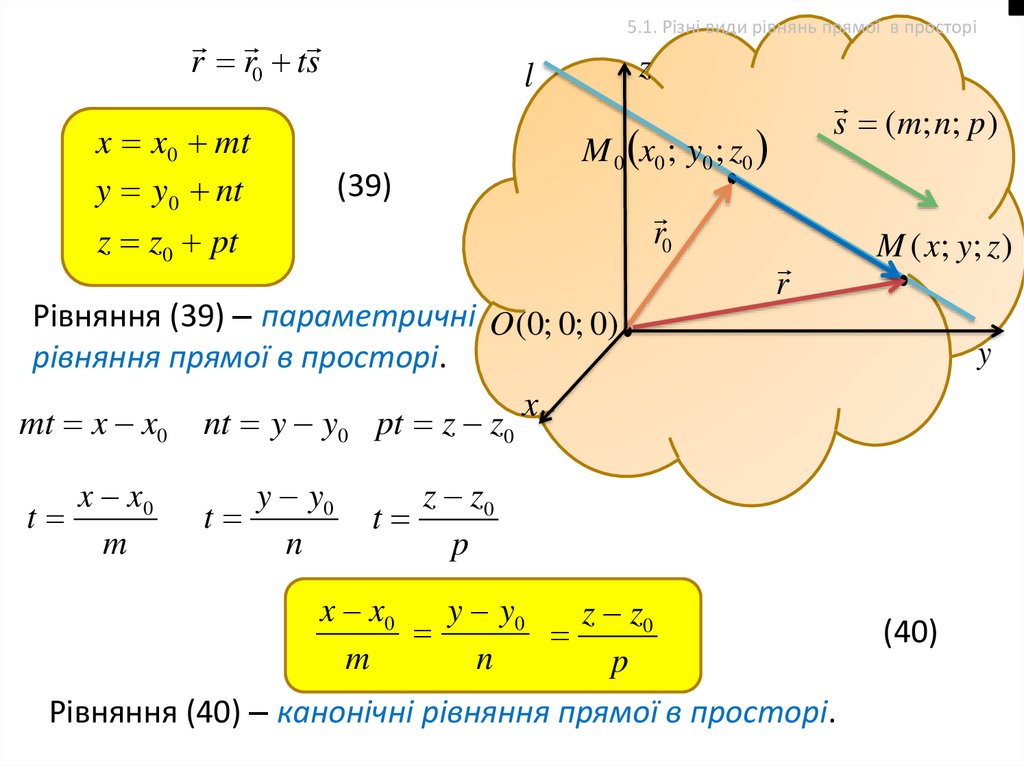
5.1. Різні види рівнянь прямої в просторіr r0 ts
x x0 mt
y y0 nt
z
l
M 0 x0 ; y0 ; z0
(39)
r0
z z0 pt
Рівняння (39) – параметричні O (0; 0; 0)
рівняння прямої в просторі.
x
mt x x0 nt y y0 pt z z0
t
x x0
m
t
y y0
n
t
s ( m; n; p )
r
M ( x; y ; z )
y
z z0
p
x x0
y y0
z z0
m
n
p
Рівняння (40) – канонічні рівняння прямої в просторі.
(40)
26.
5.1. Різні види рівнянь прямої в просторіm=0
n=0
p=0
m=n=0
m=p=0
n=p=0
s (0; n; p )
s ( m;0; p )
s ( m; n;0)
s (0;0; p )
s (0; n;0)
s (m;0;0)
s Ox
s Oy
s Oz
s || Oz
s || Oy
s || Ox
l Ox
l Oy
l Oz
l || Oz
l || Oy
l || Ox
Приклад.
Скласти рівняння прямої,
що проходить через точку А(3; 4; –2)
паралельно вектору s = (5; –6; 7).
x 3 y 4 z 2
.
5
6
7
27.
5.1. Різні види рівнянь прямої в просторіM1 ( x1; y1; z1 )
M 2 ( x2 ; y2 ; z2 )
s M1M 2 ( x2 x1; y2 y1; z2 z1 )
x x1
y y1
z z1
x2 x1 y2 y1 z2 z1
(41)
Рівняння (41) – рівняння прямої в просторі, яка проходить через
дві задані точки.
Приклад.
Скласти рівняння прямої, що проходить через точки А(3; 4; 1) і
B(5; 7; 0).
x 3 y 4 z 1
5 3 7 4 0 1
x 3 y 4 z 1
.
2
3
1
28.
5.1. Різні види рівнянь прямої в просторі1 : A1x B1 y C1z D1 0
(42)
2 : A2 x B2 y C2 z D2 0
Рівняння (42) називаються
загальними рівняннями прямої
в просторі.
n1 ( A1; B1; C1 )
n2 ( A2 ; B2 ; C2 )
s n1
s n1 n2
s n2
M 0 ( x0 ; y0 ; z0 )
x x0
1
M0
s
n1
2
n2
l
B1 y C1z D1 A1 x0 ;
B1 C1
0
B
y
C
z
D
A
x
.
B2 C2
2
2
2 0
2
x x0
y y0
z z0
m
n
p
y y0
z z0
29.
5.2. Кут між двома прямими. Умови паралельностіі перпендикулярності прямих
l1 :
x x1 y y1 z z1
m1
n1
p1
s1 (m1; n1; p1 )
l1 ,l2 s1 , s2
l2 :
x x2 y y 2 z z 2
m2
n2
p2
s2 (m2 ; n2 ; p2 )
0
2
m1m2 n1n2 p1 p2
s1 s2
cos
s1 s2
m12 n12 p12 m22 n22 p22
l1 || l2
m1 n1 p1
(45)
m2 n2 p2
l1 l2
(44)
m1m2 n1n2 p1 p2 0 (46)
30.
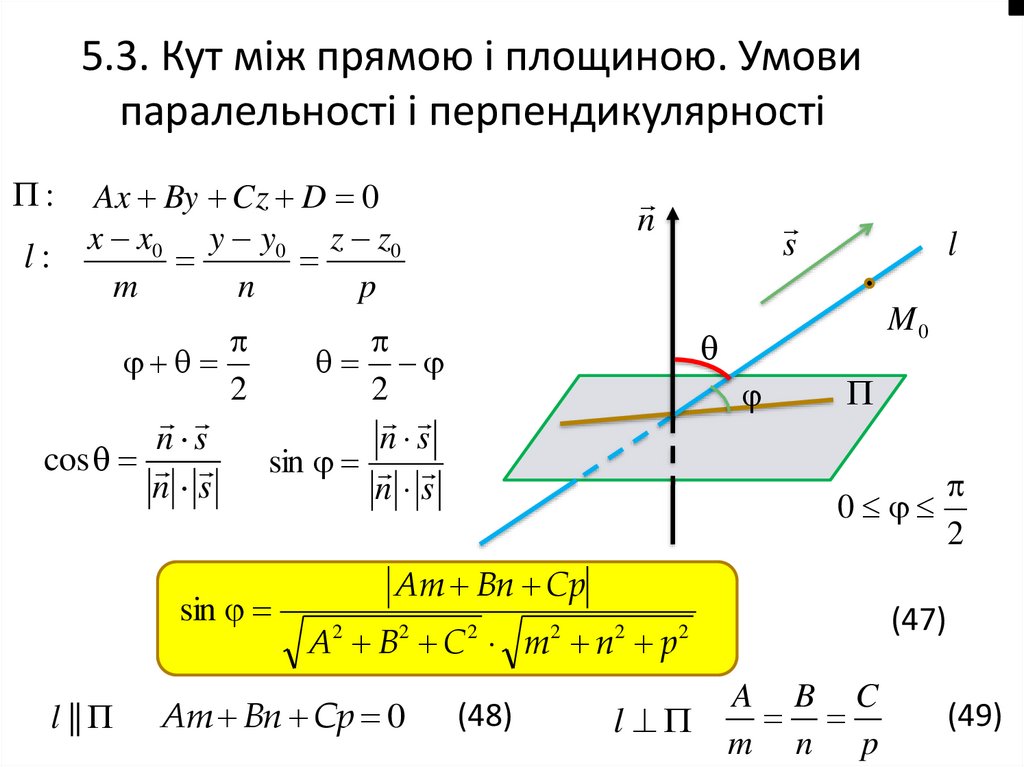
5.3. Кут між прямою і площиною. Умовипаралельності і перпендикулярності
:
l:
Ax By Cz D 0
x x0 y y0 z z0
m
n
p
n
s
2
2
n s
n s
cos
sin
n s
n s
sin
l ||
l
M0
0
2
Am Bn Cp
A B C m n p
2
2
Am Bn Cp 0
2
(48)
2
2
(47)
2
l
A B C
m n p
(49)
31.
5.4. Відстань від точки до прямоїl:
s
x x1 y y1 z z1
m
n
p
s ( m; n; p )
M1
l
M1 ( x1; y1; z1 )
d
h
M 0 ( x0 ; y0 ; z0 )
M0
M
M
s
Sпарал
0
1
d h
.
s
s
d
x1 x0
m
y1 y0
x1 x0
n
m
2
z1 z0
y1 y0
p
n
2
m n p
2
2
2
z1 z0
p
2
.
32.
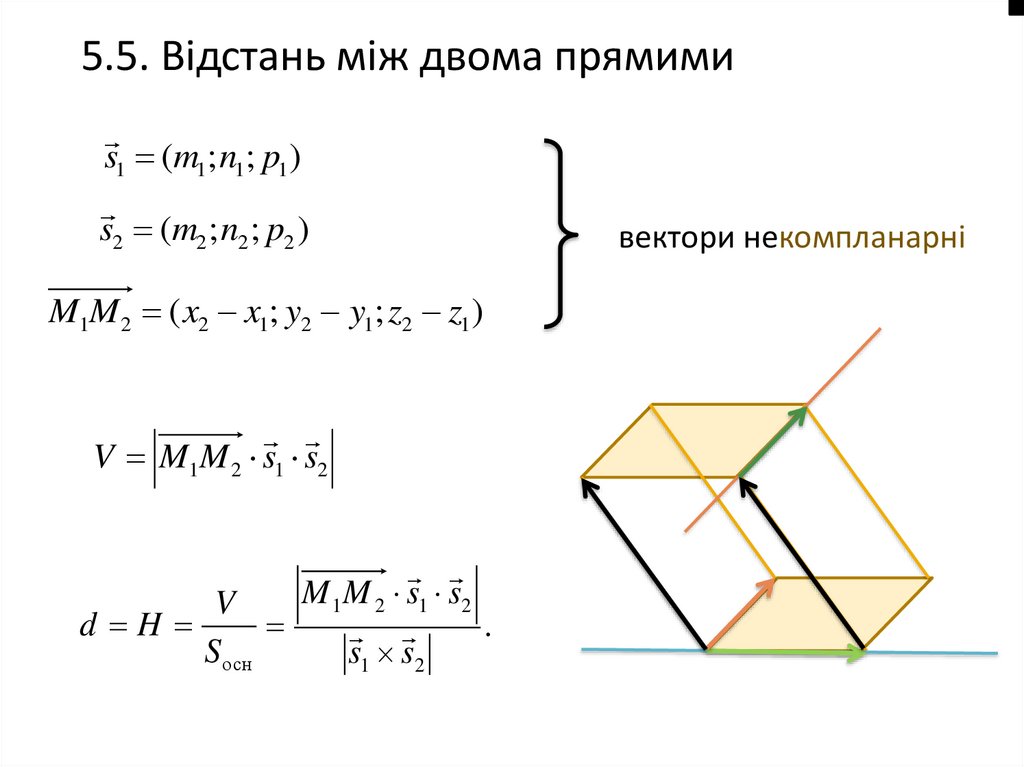
5.5. Відстань між двома прямимиs1 (m1; n1; p1 )
s2 (m2 ; n2 ; p2 )
M1M 2 ( x2 x1; y2 y1; z2 z1 )
V M1M 2 s1 s2
M
M
s
1
2
1 s2
V
d H
.
Sосн
s1 s2
вектори некомпланарні
33.
s1 (m1; n1; p1 )s2 (m2 ; n2 ; p2 )
вектори компланарні
M1M 2 ( x2 x1; y2 y1; z2 z1 )
V M1M 2 s1 s2 0
x1 x2
m1
m2
y 1 y 2
n1
n2
z1 z 2
p1 0.
p2
прямі перетинаються
(у просторі)
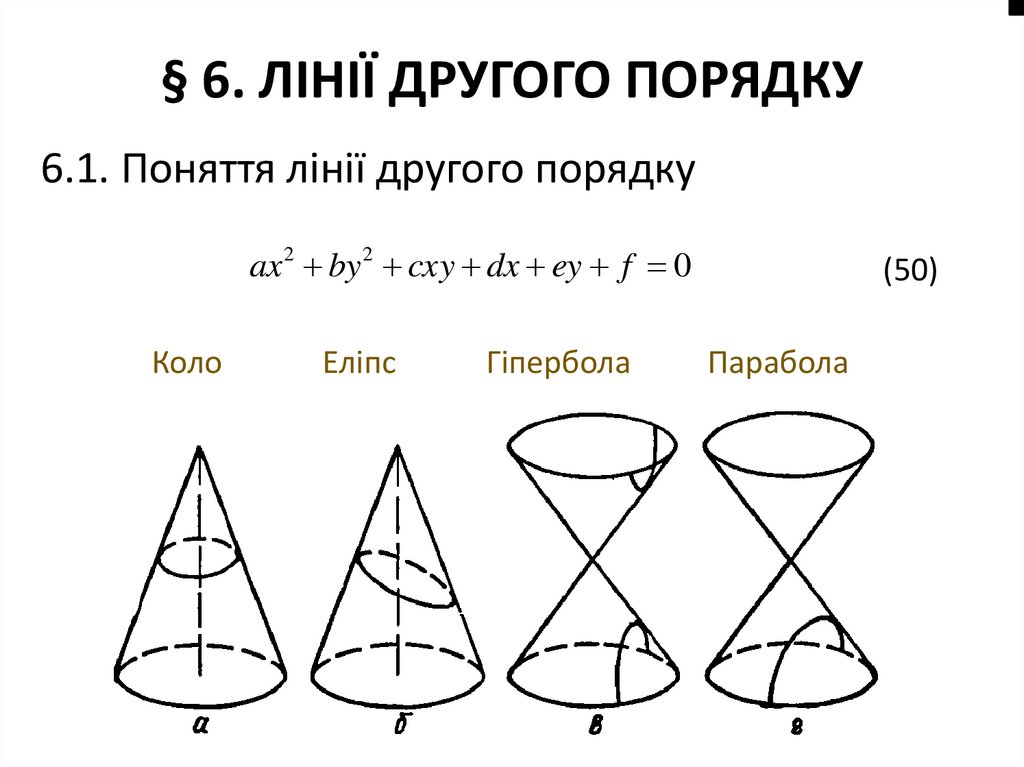
34. § 6. ЛІНІЇ ДРУГОГО ПОРЯДКУ
6.1. Поняття лінії другого порядкуax 2 by 2 cxy dx ey f 0
Коло
Еліпс
Гіпербола
(50)
Парабола
35.
6.2. КолоКолом називають множину точок площини, відстані яких від
заданої точки площини (центра кола) дорівнюють сталому
числу (радіусу).
y
M x; y
O1 a; b M x; y
O1M R
O1
b
x a 2 y b 2 R
x a 2 y b 2 R 2
(52)
x2 y 2 R2
(53)
O
a
Рівняння (53) називається канонічним рівнянням кола.
x
36.
6.2. Колоx a 2 y b 2 R 2
x 2 2 xa a 2 y 2 2 yb b2 R 2
x 2 y 2 Ax By C 0
(54)
Рівняння (54) називається загальним рівнянням кола.
1°. Коефіцієнти при х2 і у2 рівні між собою.
2°. У рівнянні відсутній член з добутком ху.
37.
6.3. ЕліпсЕліпсом називають множину всіх точок площини, сума
відстаней яких від двох даних точок цієї площини (фокусів) є
величина стала і більша від відстані між фокусами.
F1F2 2c
2a 2c
F1M MF2 2a
y
M ( x; y )
( x c )2 ( y 0) 2 ( x c) 2 ( y 0)2 2a
( x c ) 2 y 2 ( x c ) 2 y 2 2a
x
F1 ( c; 0)
( x c ) 2 y 2 2a ( x c ) 2 y 2
( x c) y 2a ( x c) y
2
2
2
2
2
2
O
F2 (c; 0)
38.
39.
( x c) y 2a ( x c) y2
2
2
2
2
6.3. Еліпс
2
( x c ) 2 y 2 4a 2 4a ( x c ) 2 y 2 ( x c ) 2 y 2
x 2 2cx c 2 y 2 4a 2 4a ( x c)2 y 2 x 2 2cx c 2 y 2
2cx 4a 2 4a ( x c)2 y 2 2cx
a ( x c ) 2 y 2 a 2 cx
a 2 ( x c)2 y 2 a 4 2a 2cx c2 x 2
a 2 x 2 2a 2cx a 2c2 a 2 y 2 a 4 2a 2cx c 2 x 2
a 2 x 2 a 2c 2 a 2 y 2 a 4 c 2 x 2
a 2 x 2 c 2 x 2 a 2 y 2 a 4 a 2c 2
40.
6.3. Еліпсa 2 x 2 c 2 x 2 a 2 y 2 a 4 a 2c 2
x 2 a 2 c2 a 2 y 2 a 2 a 2 c 2
a 2 c2 0
b2 a 2 c 2
(56)
x 2b 2 a 2 y 2 a 2b 2
x2 y2
2 1
2
a
b
(57)
Рівняння (57) називається канонічним рівнянням еліпса.
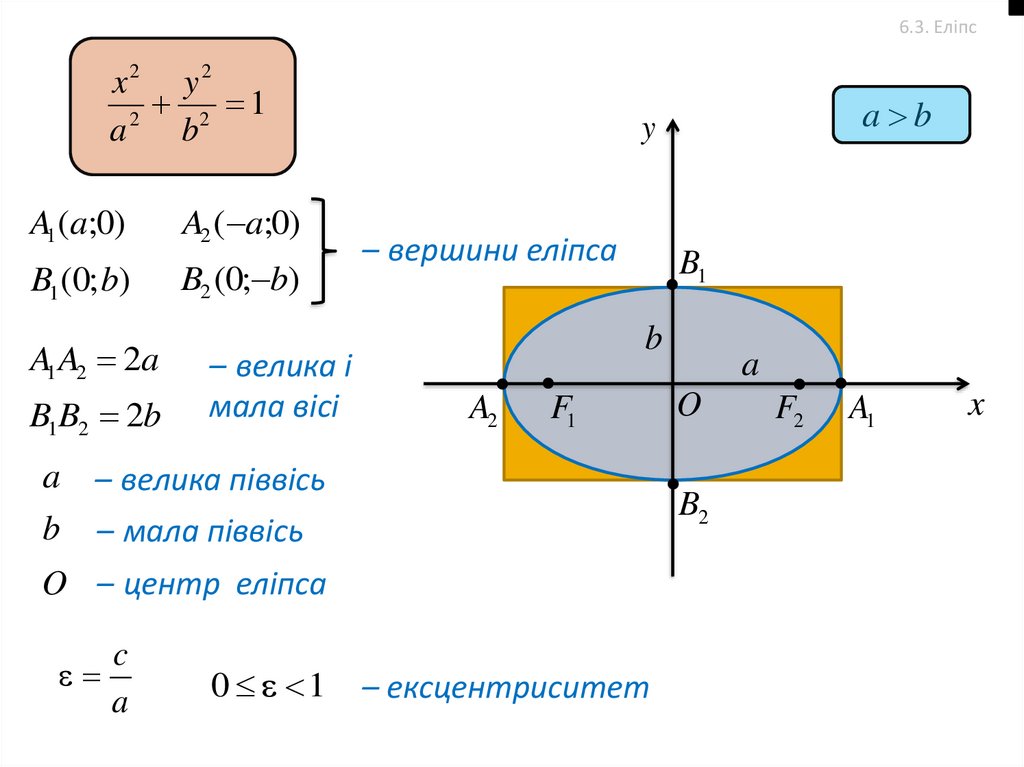
41.
6.3. Еліпсx2 y2
2 1
2
a
b
A1 (a;0)
A2 ( a;0)
B1 (0; b)
B2 (0; b)
A1 A2 2a
B1B2 2b
– велика і
мала вісі
– вершини еліпса
B1
b
A2
F1
a – велика піввісь
b – мала піввісь
O – центр еліпса
c
a
0 1
a b
y
a
O
B2
– ексцентриситет
F2
A1
x
42.
6.3. Еліпсx2 y2
2 1
2
a
b
a b
a b
y
b2 a 2 c 2
x2 y2 a2
0
c 0
b
a
O
a b
c
a
1
0 1
– ексцентриситет
x
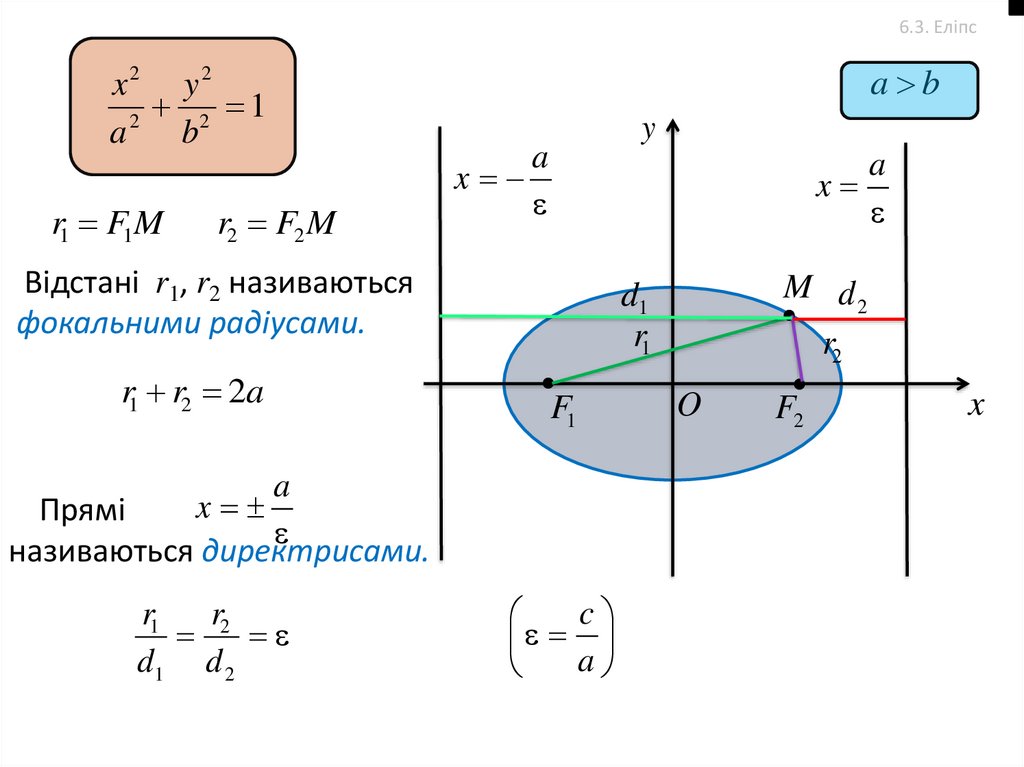
43.
6.3. Еліпсx2 y2
2 1
2
a
b
r1 F1M
r2 F2 M
a b
y
a
x
x
Відстані r1, r2 називаються
фокальними радіусами.
r1 r2 2a
a
x
Прямі
називаються директрисами.
r1
r2
d1 d 2
M d2
r2
d1
r1
F1
c
a
a
O
F2
x
44.
26.3. Еліпс
2
x
y
2 1
2
a
b
a b
a b
F2
F1
F1F2 2c
r1
r2
d1 d 2
F2
r1 r2 2a
F1, F2 Ox
r1 r2 2b
F1, F2 Oy
F1, 2 ( c; 0)
A1 A2 2a
c
1
a
a 2 b2 c 2
a
x
– велика вісь –
x x0 2 y y0 2 1
a2
b2
F1
F1, 2 (0; c )
B1B2 2b
c
1
b
b2 a 2 c 2
b
y
45.
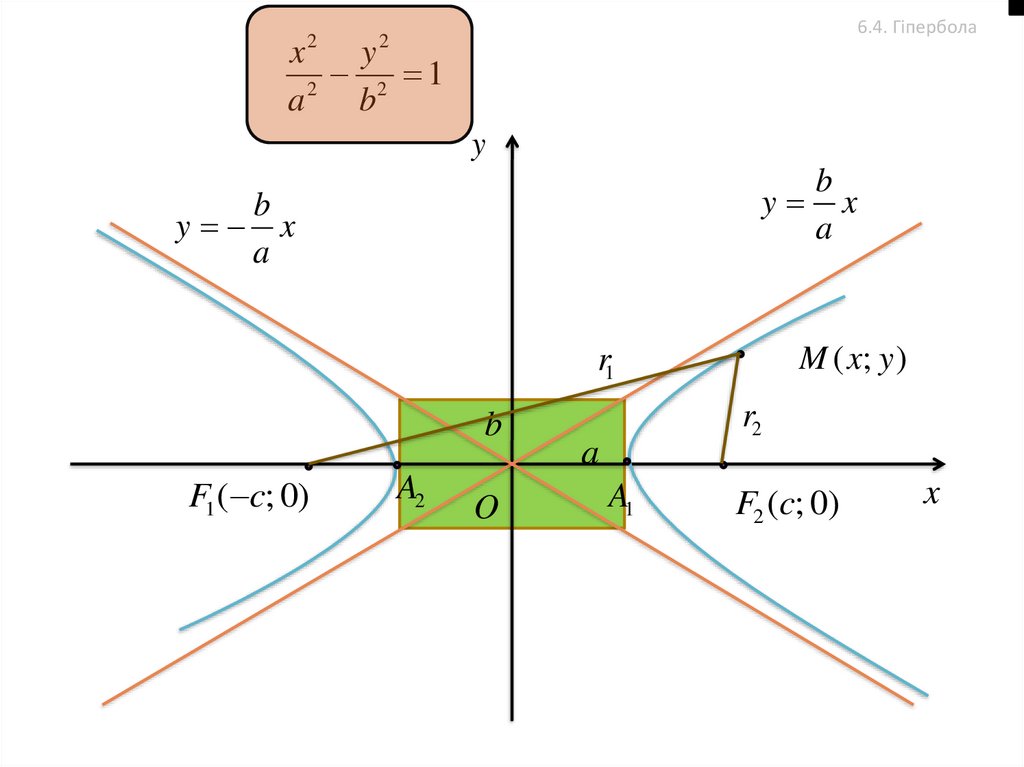
6.4. ГіперболаГіперболою називається множина всіх точок площини, модуль
різниці відстаней яких від двох даних точок цієї площини
(фокусів) є величина стала і менша відстані між фокусами.
F1F2 2c
y
F1M MF2 2a
2a 2c
M ( x; y )
( x c ) 2 ( y 0)2 ( x c )2 ( y 0)2 2a
x2 y2
2 1
2
a
b
x
(61)
F1 ( c; 0)
O
F2 (c; 0)
Рівняння (61) називається канонічним рівнянням гіперболи.
b2 c 2 a 2
a 2 b2 c 2
46.
26.4. Гіпербола
2
x
y
2 1
2
a
b
y
y
b
y x
a
b
x
a
M ( x; y )
r1
b
F1 ( c; 0)
A2
O
r2
a
A1
F2 (c; 0)
x
47.
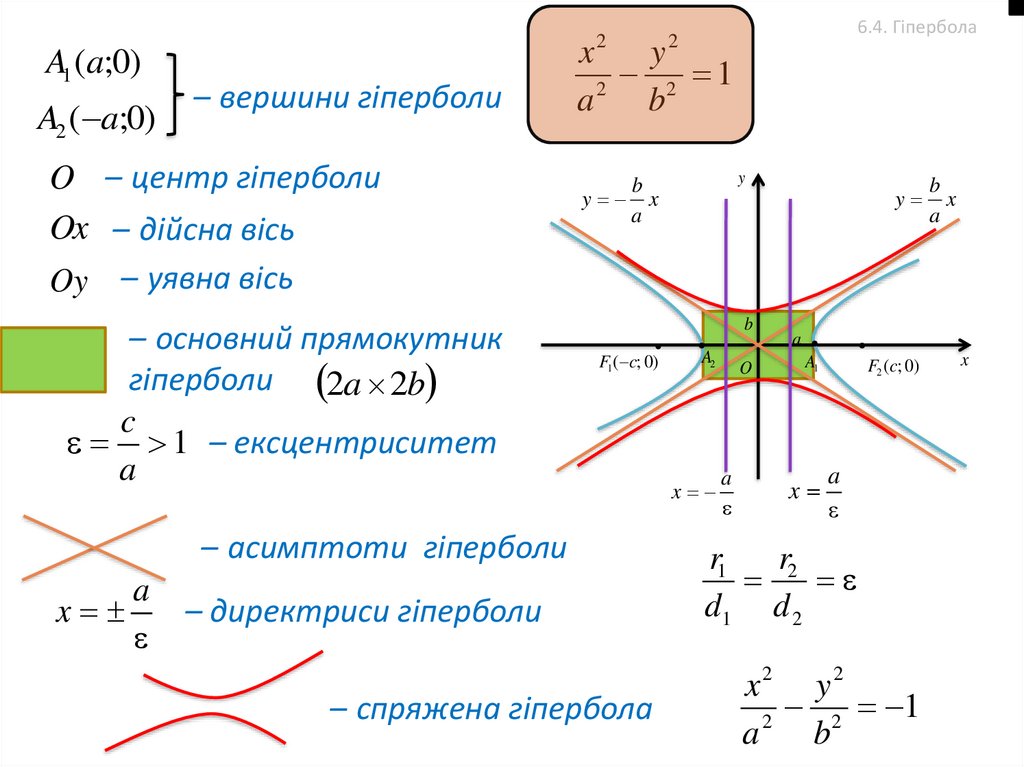
A1 (a;0)A2 ( a;0)
2
– вершини гіперболи
O – центр гіперболи
Ox – дійсна вісь
Oy – уявна вісь
– основний прямокутник
гіперболи 2a 2b
c
1 – ексцентриситет
a
x
y
2 1
2
a
b
y
b
y x
a
b
F1 ( c; 0)
– асимптоти гіперболи
a
x
6.4. Гіпербола
2
– директриси гіперболи
– спряжена гіпербола
A2
x
O
a
y
b
x
a
a
A1
x
F2 (c; 0)
a
r1
r2
d1 d 2
x2 y2
2 1
2
a
b
x
48.
6.5. ПараболаПараболою називається множина всіх точок площини, кожна
з яких знаходиться на однаковій відстані від даної точки
(фокуса) і від прямої даної (директриси).
B
MF BM
y
M ( x; y )
2
p
p
2
x y 0 x
2
2
2
2
p
p
x 2 px
y 2 x 2 px
4
4
y 2 2 px
(68)
x
p
2
O
p
F ; 0
2
Рівняння (68) називається канонічним рівнянням параболи.
49.
6.5. Параболаy 2 2 px
B
y
M ( x; y )
O – вершина параболи
p – параметр
x
p
– директриса
2
r
1 – ексцентриситет
d
p
r d x
2
r MF
d MB
x
p
2
O
p
F ; 0
2
50.
y 2 2 pxy 2 px
p
x
2
2
p
x
2
y y0 2 2 p x x0
p
r d x
2
6.5. Парабола
y 2 2 px
p
x
2
x 2 2 py
x x0 2 p y y0
2
x 2 2 py
p
y
2
p
r d y
2
p
y
2
51. § 7. ПОВЕРХНІ ДРУГОГО ПОРЯДКУ
7.1. Поняття поверхні другого порядкуax 2 by 2 cz 2 dxy exz fyz gx hy kz l 0
7.2. Циліндричні поверхні
Циліндричною поверхнею
називають поверхню σ,
утворену множиною прямих
(твірних), які перетинають
задану лінію L (напрямну) і
паралельні заданій прямій l
(74)
52.
7.3. Поверхні обертанняПоверхню, утворену обертанням заданої плоскої
кривої l навколо заданої прямої (осі обертання), яка
лежить в площині кривої l, називають поверхнею
обертання.
53.
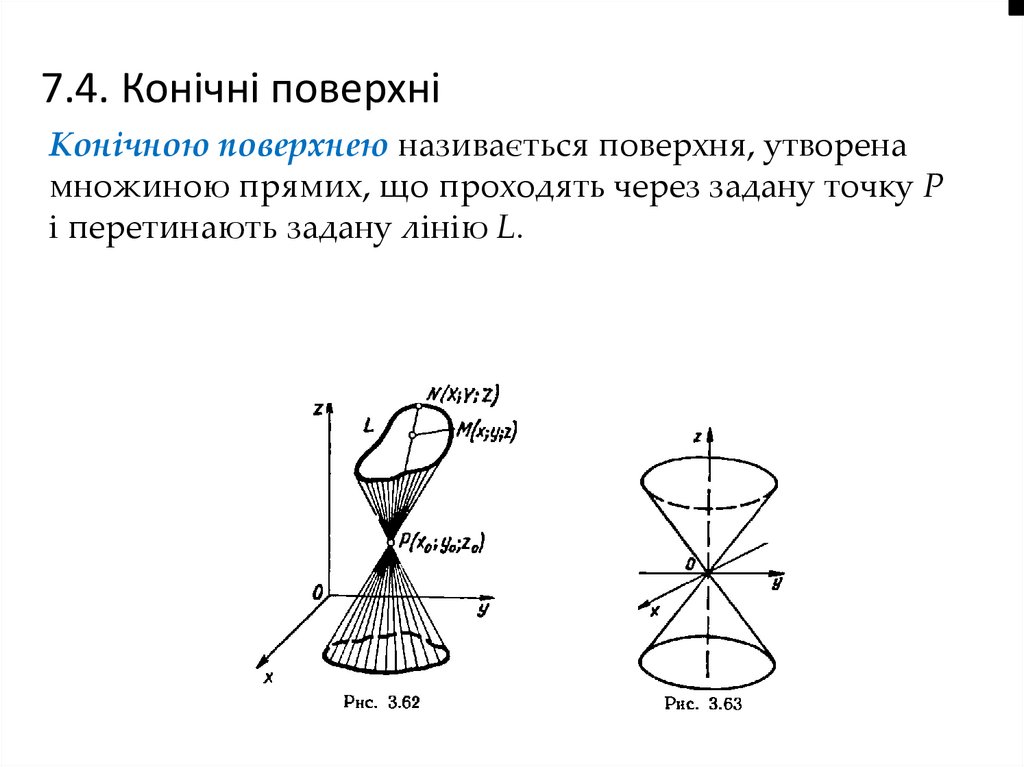
7.4. Конічні поверхніКонічною поверхнею називається поверхня, утворена
множиною прямих, що проходять через задану точку Р
і перетинають задану лінію L.
54.
7.5. СфераСферою називають множину всіх точок простору,
рівновіддалених від заданої точки, яка називається
центром.
x a 2 y b 2 z c 2 R2
(79)
55.
7.6. ЕліпсоїдЕліпсоїдом називається поверхня, яка в деякій
прямокутній системі координат визначається рівнянням
x2 y 2 z2
2 2 1
2
a
b
c
(81)
56.
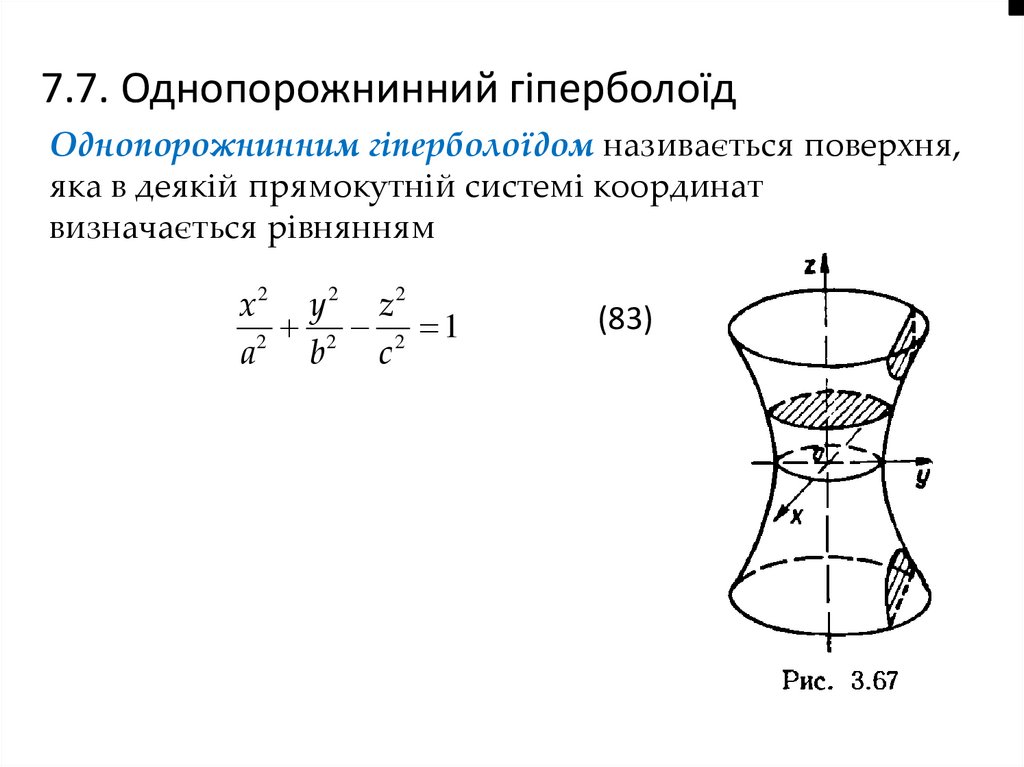
7.7. Однопорожнинний гіперболоїдОднопорожнинним гіперболоїдом називається поверхня,
яка в деякій прямокутній системі координат
визначається рівнянням
x2 y 2 z2
2 2 1
2
a
b
c
(83)
57.
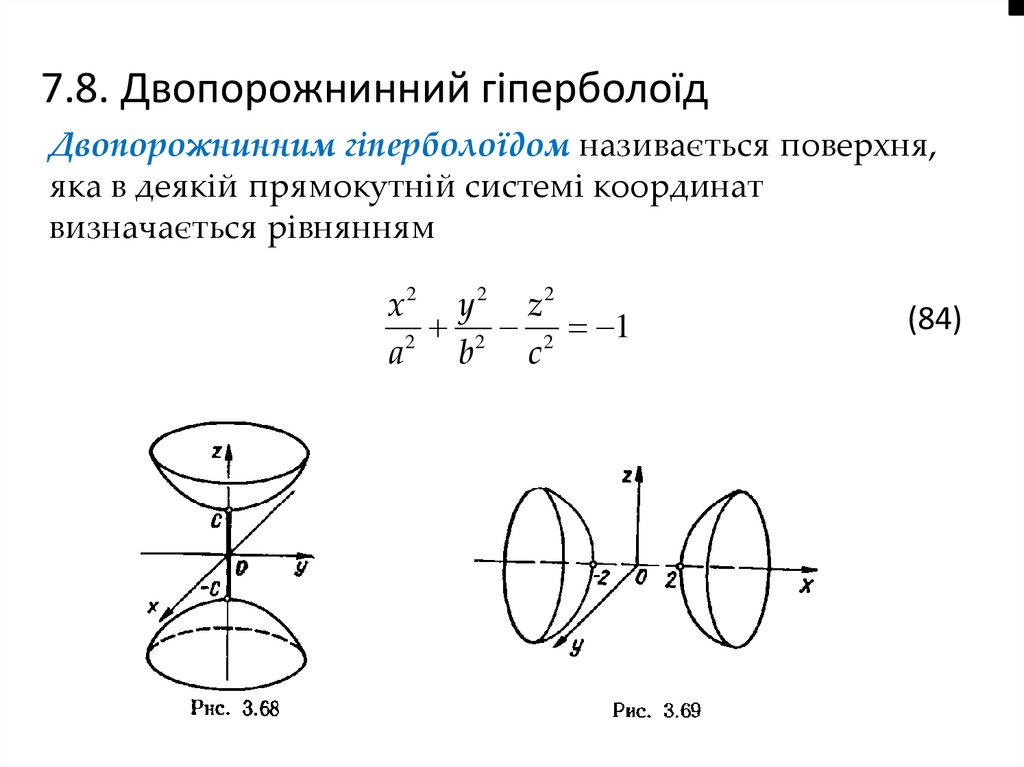
7.8. Двопорожнинний гіперболоїдДвопорожнинним гіперболоїдом називається поверхня,
яка в деякій прямокутній системі координат
визначається рівнянням
x2 y 2 z2
2 2 1
2
a
b
c
(84)
58.
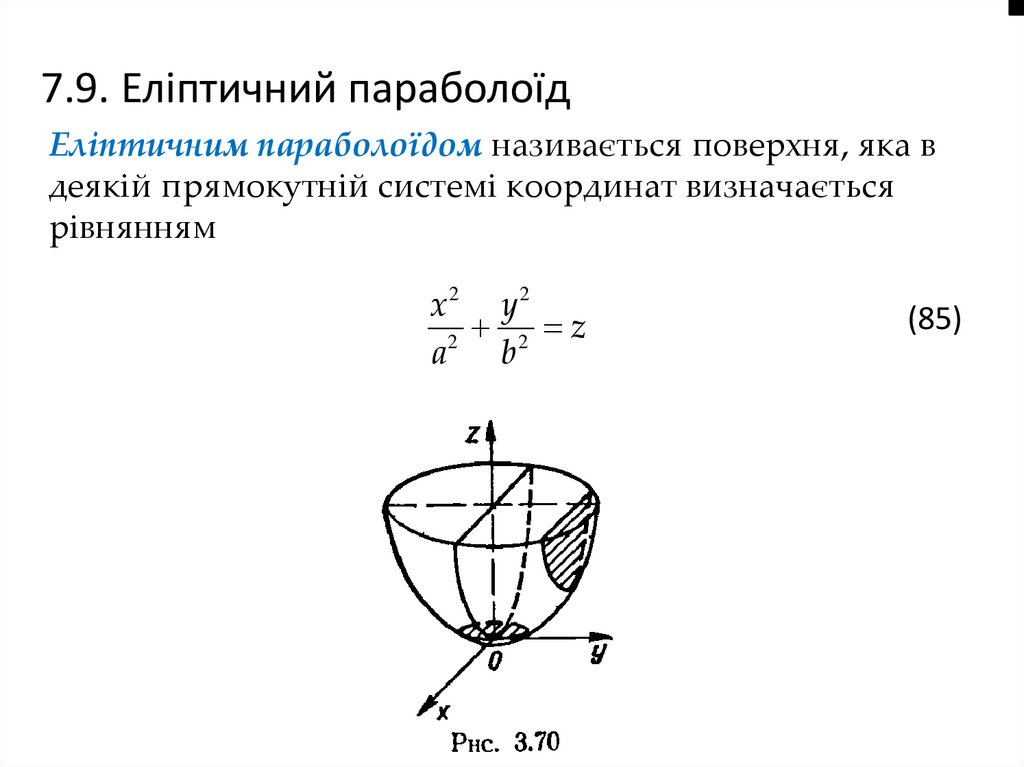
7.9. Еліптичний параболоїдЕліптичним параболоїдом називається поверхня, яка в
деякій прямокутній системі координат визначається
рівнянням
x2 y 2
2 z
2
a
b
(85)
59.
7.10. Гіперболічний параболоїдГіперболічним параболоїдом називається поверхня, яка в
деякій прямокутній системі координат визначається
рівнянням
x2 y 2
2 z
2
a
b
(86)

























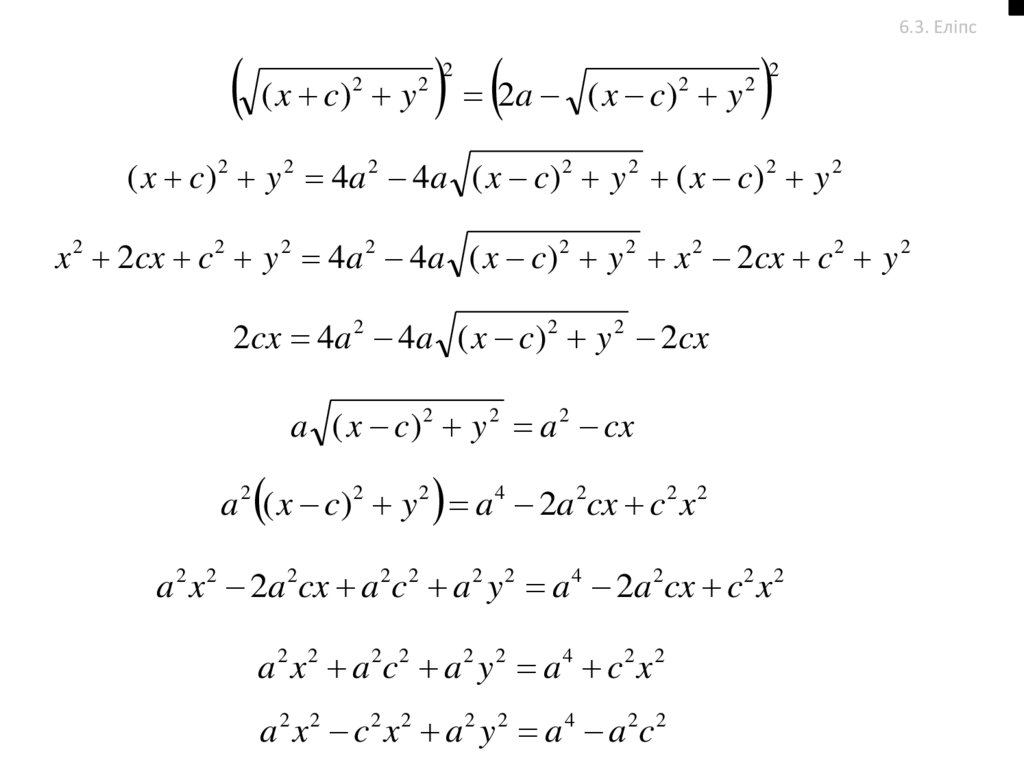












 Математика
Математика








