Методы формирования и преобразования сигналов

1.

Инженерный факультет
Кафедра инфокоммуникационных технологий и систем связи
Учебная дисциплина
«Общая теория связи»
Доцент кафедры (инфокоммуникационных технологий
и систем связи)
Ефимова Екатерина Витальевна

2.

ТЕМА № 3
Методы формирования и преобразования сигналов.
Модуляция и детектирование
Лекция № 3.1
Методы формирования и преобразования сигналов
УЧЕБНЫЕ ВОПРОСЫ:
1. Формирование и детектирование сигналов при передаче непрерывных
сообщений.
2. Формирование и детектирование сигналов при передаче дискретных
сообщений.
2

3. Литература

а) основная литература:
1. Зверев А.П. Общая теория связи. Часть 1. Химки 2014.- 196с.
б) дополнительная литература:
2.Прокис Дж. Цифровая связь: Пер. с англ. / Под ред. Д.Д. Кловского. – М.: Радио и связь, 2000. – 800 с.
3.Бернард Скляр. Цифровая связь. Теоретические основы и практическое применение: Пер. с англ. – М.:
Издательский дом «Вильямс», 2003. – 1104 с.
4.Сухоруков А.С. Теория электрической связи: Конспект лекций. Часть 1. – М.:МТУСИ, ЦЕНТР ДО, 2002. – 65 с.
5.Сухоруков А.С. Теория цифровой связи: Учебное пособие. Часть 2. – М.:МТУСИ, 2008. – 53 с.
3

4. 1 учебный вопрос ФОРМИРОВАНИЕ И ДЕТЕКТИРОВАНИЕ СИГНАЛОВ ПРИ ПЕРЕДАЧЕ НЕПРЕРЫВНЫХ СООБЩЕНИЙ.

4

5.

ОПРЕДЕЛЕНИЕ МОДУЛЯЦИИ
Модуляция (лат. modulatio — размеренность, ритмичность) — процесс изменения
одного или нескольких параметров высокочастотного несущего колебания по закону
низкочастотного информационного сигнала (сообщения)
Условное графическое
обозначение
модулятора
При модуляции на вход модулятора подаются сигналы:
u(t) — модулирующий, данный сигнал является
информационным и низкочастотным (его частоту
обозначают W или F);
S(t) — модулируемый (несущий), данный сигнал
является неинформационным
и высокочастотным (его частота обозначается w0 или f0);
Sм(t) — модулированный сигнал, данный сигнал
является информационным и высокочастотным.
Передаваемая
информация
заложена
в
управляющем
(модулирующем) сигнале, а роль переносчика информации
выполняет несущий (модулируемый) сигнал. Модуляция
представляет собой процесс «посадки» информационного
колебания на заведомо известную несущую с целью получения
нового, модулированного сигнала.

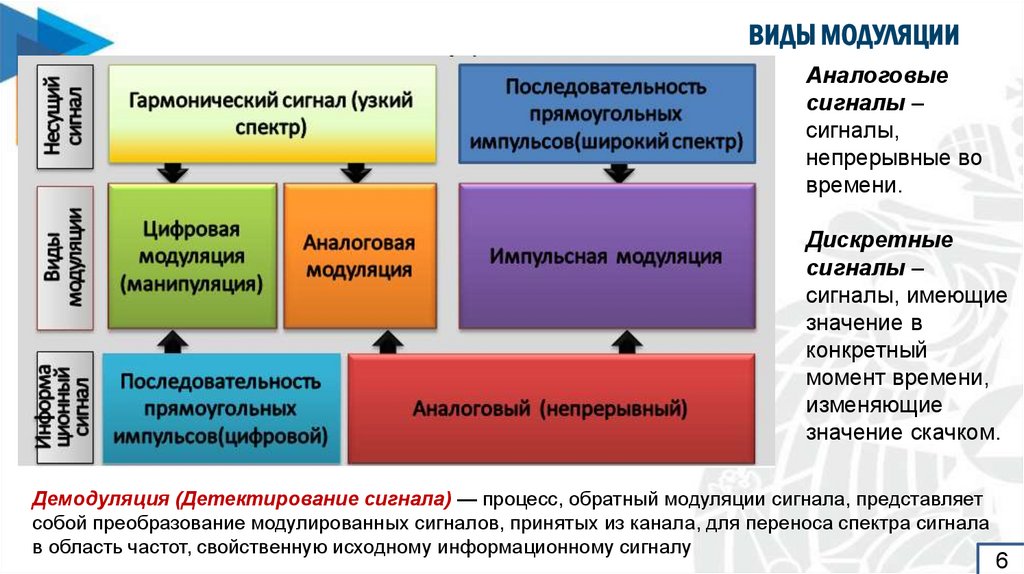
6. ВИДЫ МОДУЛЯЦИИ

Аналоговые
сигналы –
сигналы,
непрерывные во
времени.
Дискретные
сигналы –
сигналы, имеющие
значение в
конкретный
момент времени,
изменяющие
значение скачком.
Демодуляция (Детектирование сигнала) — процесс, обратный модуляции сигнала, представляет
собой преобразование модулированных сигналов, принятых из канала, для переноса спектра сигнала
в область частот, свойственную исходному информационному сигналу
6

7. АНАЛОГОВАЯ МОДУЛЯЦИЯ

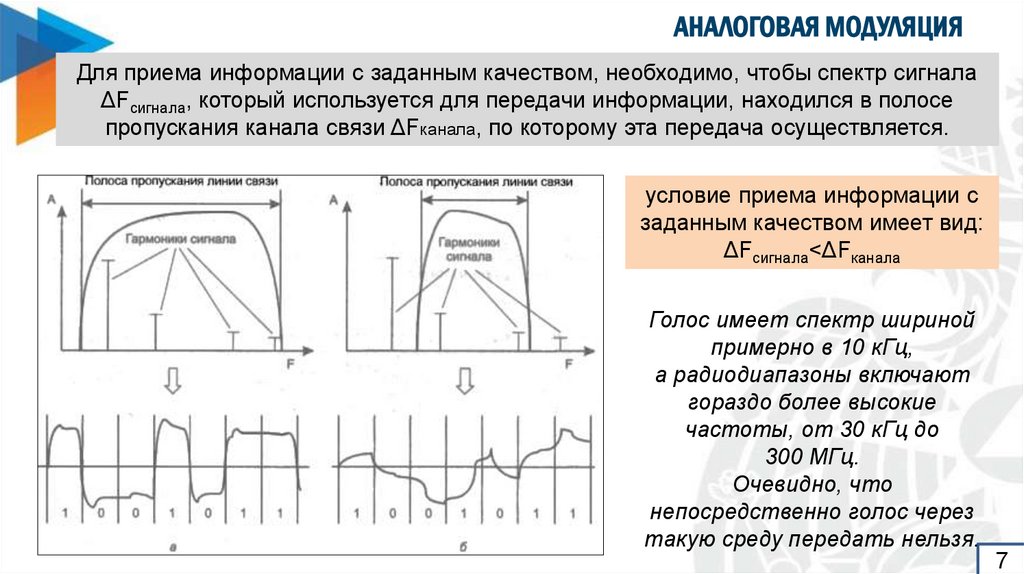
Для приема информации с заданным качеством, необходимо, чтобы спектр сигнала
ΔFсигнала, который используется для передачи информации, находился в полосе
пропускания канала связи ΔFканала, по которому эта передача осуществляется.
условие приема информации с
заданным качеством имеет вид:
ΔFсигнала<ΔFканала
Голос имеет спектр шириной
примерно в 10 кГц,
а радиодиапазоны включают
гораздо более высокие
частоты, от 30 кГц до
300 МГц.
Очевидно, что
непосредственно голос через
такую среду передать нельзя.
7

8. ПОЛОСА ПРОПУСКАНИЯ ЛИНИЙ СВЯЗИ РАЗЛИЧНЫХ ТИПОВ И НАИБОЛЕЕ ЧАСТО ИСПОЛЬЗУЕМЫЕ В ТЕХНИКЕ СВЯЗИ ЧАСТОТНЫЕ ДИАПАЗОНЫ

8

9. АНАЛОГОВАЯ МОДУЛЯЦИЯ

Тот параметр, который в результате модуляции изменяется в соответствии с
изменением информационного сигнала, называется информационным
параметром.
9

10. АМПЛИТУДНАЯ МОДУЛЯЦИЯ

Амплитудная модуляция (amplitude modulation (AM) — процесс
изменения амплитуды несущего сигнала, как правило высокочастотного
синусоидального колебания, в соответствии с мгновенными значениями
информационного аналогового сигнала.
Математическая модель амплитудно-модулированного (АМ)
сигнала при гармоническом модулирующем сигнале
При воздействии модулирующего сигнала
u(t)=Umu sinωt (1)
на несущее колебание
S(t)=Um sin(ω0t+φ) (2)
происходит изменение амплитуды несущего сигнала по закону:
Uам(t)=Um+аам Umu sinωt (3)
где аам — коэффициент пропорциональности амплитудной модуляции.
Подставив (3) в математическую модель (2) получим:
Sам(t)=(Um+аам Umu sinωt) sin(ω0t+φ) (4)
или
Sам(t)=Um(1+аам (Umu/Um) sinω t) sin(ω0t+φ) (5)
аам (Umu/Um) = mам называется коэффициентом амплитудной модуляции.
10

11. АМПЛИТУДНАЯ МОДУЛЯЦИЯ

С учетом mам математическая модель АМ сигнала при гармоническом
модулирующем сигнале будет иметь вид:
Sам(t)=Um(1+mам sinω t) sin(ω0t+φ).
Рассмотрим спектр АМ сигнала для гармонического модулирующего сигнала.
Для этого раскроем скобки математической модели модулированного
сигнала, т. е. представим его в виде суммы гармонических составляющих
Sам(t)=Um(1+mам sinω t) sin(ω0t+φ)=
=Um sin(ω0t+φ)+mамUm/2 sin((ω0 — ω) t+j) — mамUm/2 sin((ω0 +ω)t+j).
в спектре АМ сигнала присутствует три составляющих: составляющая несущего
сигнала и две полосы частот справа и слева от нее, каждая из которых имеет
ширину спектра информационного сигнала.
11

12. АМПЛИТУДНАЯ МОДУЛЯЦИЯ

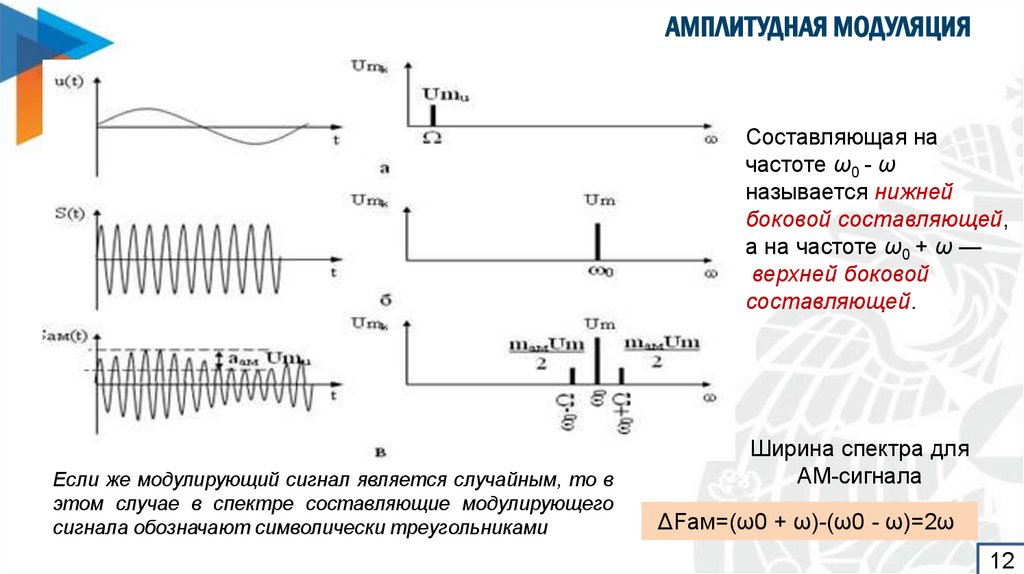
Составляющая на
частоте ω0 - ω
называется нижней
боковой составляющей,
а на частоте ω0 + ω —
верхней боковой
составляющей.
Если же модулирующий сигнал является случайным, то в
этом случае в спектре составляющие модулирующего
сигнала обозначают символически треугольниками
Ширина спектра для
АМ-сигнала
ΔFам=(ω0 + ω)-(ω0 - ω)=2ω
12

13. АМПЛИТУДНАЯ МОДУЛЯЦИЯ

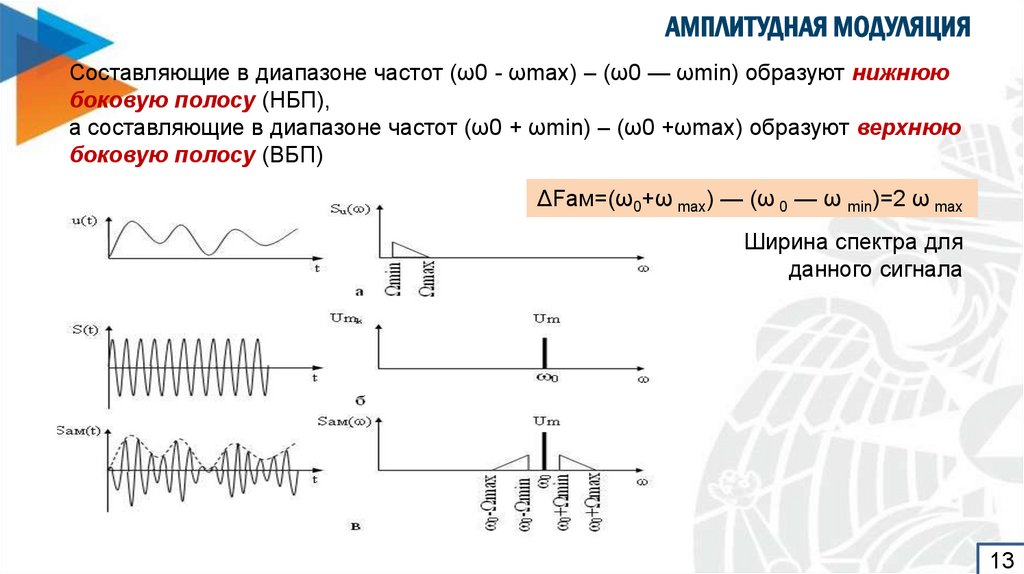
Составляющие в диапазоне частот (ω0 - ωmax) – (ω0 — ωmin) образуют нижнюю
боковую полосу (НБП),
а составляющие в диапазоне частот (ω0 + ωmin) – (ω0 +ωmax) образуют верхнюю
боковую полосу (ВБП)
ΔFам=(ω0+ω max) — (ω 0 — ω min)=2 ω max
Ширина спектра для
данного сигнала
13

14. АМПЛИТУДНАЯ МОДУЛЯЦИЯ

при mам=0 модуляция отсутствует, сигнал
представляет собой немодулированную
несущую, соответственно и спектр этого
сигнала имеет только составляющую
несущего сигнала
0< mам <1
При
индексе
модуляции
mам=1
происходит глубокая модуляция, в
спектре АМ сигнала амплитуды боковых
составляющих
равны
половине
амплитуды составляющей несущего
сигнала
При mам >1 происходит перемодуляция,
что приводит к искажению огибающей
АМ-сигнала. В спектре такого сигнала
амплитуды
боковых
составляющих
превышают
половину
амплитуды
составляющей несущего сигнала
14

15. ДОСТОИНСТВА И НЕДОСТАТКИ АМ

Основные достоинства амплитудной модуляции:
Основные недостатки амплитудной модуляции:
15

16. ПРИМЕНЕНИЕ АМ

16

17. БАЛАНСКАЯ МОДУЛЯЦИЯ

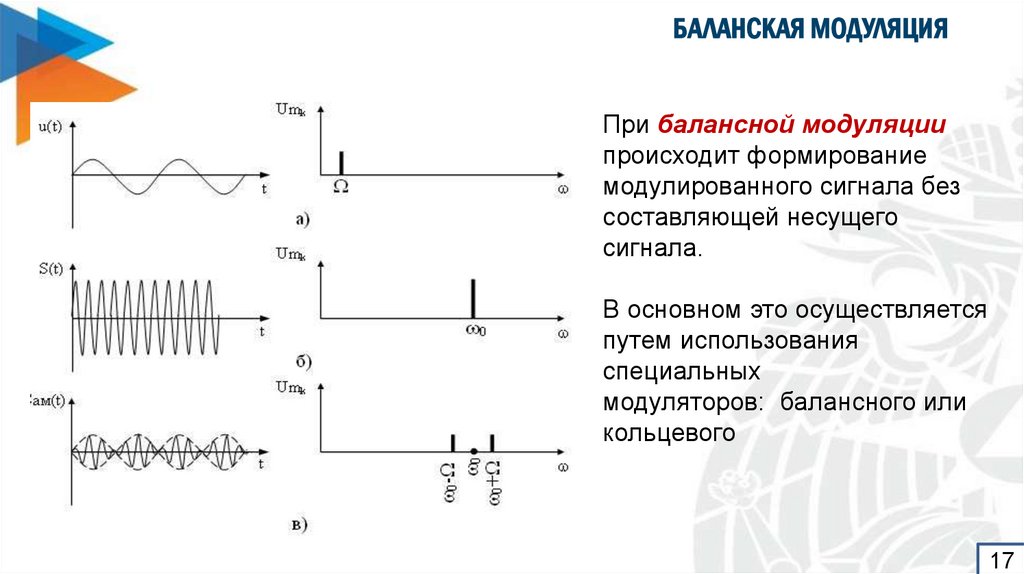
При балансной модуляции
происходит формирование
модулированного сигнала без
составляющей несущего
сигнала.
В основном это осуществляется
путем использования
специальных
модуляторов: балансного или
кольцевого
17

18. ОДНОПОЛОСНАЯ МОДУЛЯЦИЯ

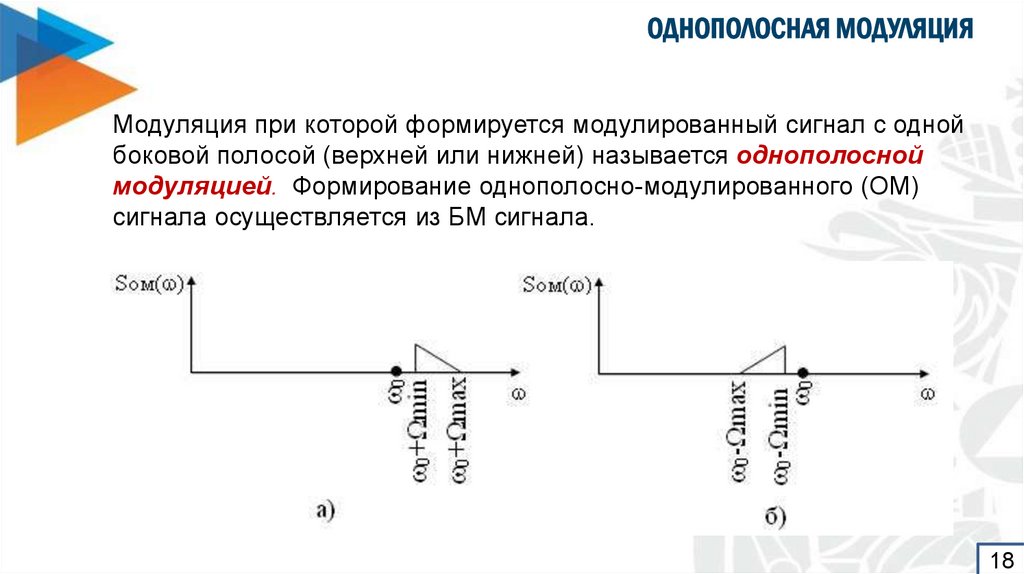
Модуляция при которой формируется модулированный сигнал с одной
боковой полосой (верхней или нижней) называется однополосной
модуляцией. Формирование однополосно-модулированного (ОМ)
сигнала осуществляется из БМ сигнала.
18

19. ЧАСТОТНАЯ МОДУЛЯЦИЯ

Частотная аналоговая модуляция (frequency modulation (FM) — процесс
изменения частоты несущего сигнала, как правило высокочастотного синусоидального
колебания, в соответствии с мгновенными значениями информационного аналогового
сигнала (как правило амплитуды).
Рассмотрим математическую модель частотно-модулированного (ЧМ) сигнала
при гармоническом модулирующем сигнале.
При воздействии модулирующего сигнала (гармоническое колебание) вида u(t) = Umu sinω t
на несущее колебание
S(t) = Um sin(ω0t+φ)
происходит изменение частоты несущего сигнала по закону: wчм(t) = ω0+ачм Umu sinω (9)
где ачм — коэффициент пропорциональности частотной модуляции.
Поскольку значение sin ωt может изменяться в диапазоне от -1 до 1, то наибольшее
отклонение частоты ЧМ сигнала от частоты несущего сигнала составляет Dwm = ачм Umu.
Величина Dwm называется девиацией частоты. Следовательно, девиация частоты
показывает наибольшее отклонение частоты модулированного сигнала от частоты
несущего сигнала.
19

20. ЧАСТОТНАЯ МОДУЛЯЦИЯ

Начальная фаза несущего сигнала определяется по формуле:
Отношение
Мчм = Dwm /ω
называется индексом частотной модуляции.
Математическая модель ЧМ сигнала при гармоническом
модулирующем сигнале будет иметь вид:
Sчм(t)=Um sin(ω 0t — Мчм cos ω t+ φ).
20

21. ЧАСТОТНАЯ МОДУЛЯЦИЯ

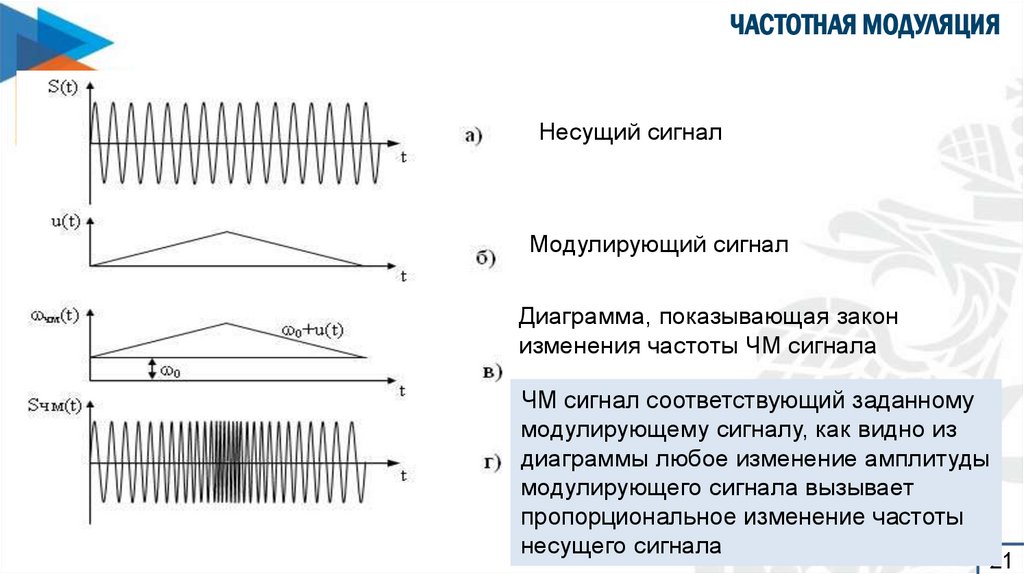
Несущий сигнал
Модулирующий сигнал
Диаграмма, показывающая закон
изменения частоты ЧМ сигнала
ЧМ сигнал соответствующий заданному
модулирующему сигналу, как видно из
диаграммы любое изменение амплитуды
модулирующего сигнала вызывает
пропорциональное изменение частоты
несущего сигнала
21

22. ЧАСТОТНАЯ МОДУЛЯЦИЯ

Для построения спектра ЧМ-сигнала необходимо разложить его
математическую модель на гармонические составляющие.
В результате разложения получим
Sчм(t)= Um J0(Mчм) sin(ω0t+φ) —
—Um J1(Mчм) {cos[(ω 0 — ω )t+j]+ cos[(ω 0+ ω)t+ φ]} —
— Um J2(Mчм) {sin[(ω 0 — 2 ω)t+j]+ sin[(ω 0+2 ω)t+ φ]}+
+ Um J3(Mчм) {cos[(ω 0 — 3 ω)t+j]+ cos[(ω 0+3 ω)t+ φ]} —
— Um J4(Mчм) {sin[(ω 0 — 4 ω)t+j]+ sin[(ω 0+4 ω)t+ φ]} —… ,
где Jk(Mчм) — коэффициенты пропорциональности, которые
определяются по функциям Бесселя и зависят от индекса частотной
модуляции.
22

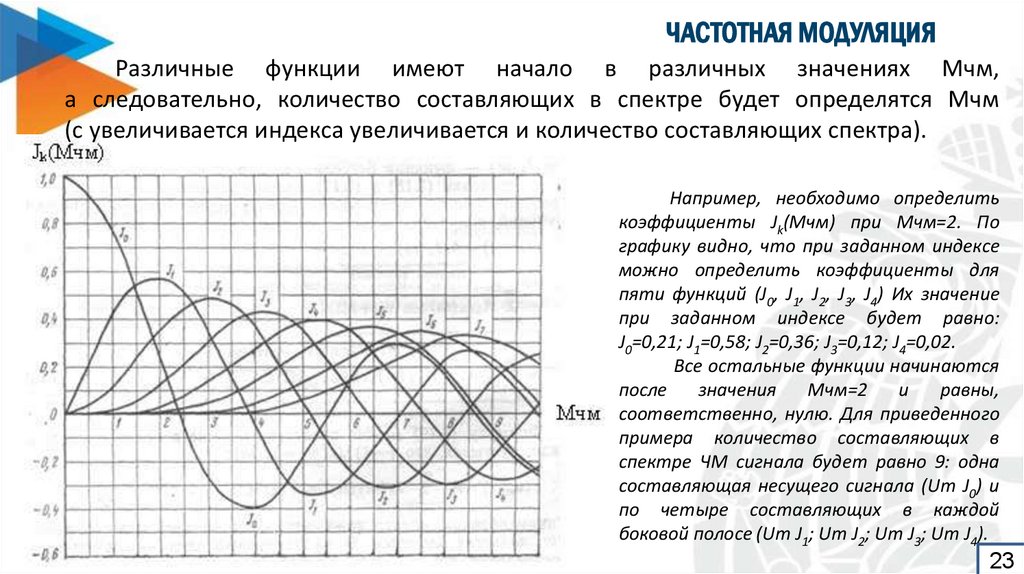
23. ЧАСТОТНАЯ МОДУЛЯЦИЯ

Различные функции имеют начало в различных значениях Мчм,
а следовательно, количество составляющих в спектре будет определятся Мчм
(с увеличивается индекса увеличивается и количество составляющих спектра).
Например, необходимо определить
коэффициенты Jk(Мчм) при Мчм=2. По
графику видно, что при заданном индексе
можно определить коэффициенты для
пяти функций (J0, J1, J2, J3, J4) Их значение
при заданном индексе будет равно:
J0=0,21; J1=0,58; J2=0,36; J3=0,12; J4=0,02.
Все остальные функции начинаются
после
значения
Мчм=2
и
равны,
соответственно, нулю. Для приведенного
примера количество составляющих в
спектре ЧМ сигнала будет равно 9: одна
составляющая несущего сигнала (Um J0) и
по четыре составляющих в каждой
боковой полосе (Um J1; Um J2; Um J3; Um J4).
23

24. ЧАСТОТНАЯ МОДУЛЯЦИЯ

Можно добиться отсутствия составляющей несущего сигнала или сделать ее
амплитуду значительно меньше амплитуд информационных составляющих без
дополнительных технических усложнений модулятора.
Для этого необходимо подобрать такой индекс модуляции Мчм, при котором
J0(Мчм) будет равно нулю (в месте пересечения функции J0 с осью Мчм), например,
Мчм=2,4.
Поскольку увеличение составляющих приводит к увеличению ширины спектра
ЧМ сигнала, то значит, ширина спектра зависит от Мчм.
При Мчм ≤0,5 ширина спектра ЧМ сигнала соответствует ширине спектра АМ
сигнала и в этом случае частотная модуляция является узкополосной, при
увеличении Мчм ширина спектра увеличивается, и модуляция в этом случае
является широкополосной.
Для ЧМ сигнала ширина спектра определяется
Dωчм=2(1+Мчмω).
24

25. ЧАСТОТНАЯ МОДУЛЯЦИЯ

Основные достоинства частотной модуляции:
Основной недостаток частотной модуляции:
25

26. ПРИМЕНЕНИЕ ЧАСТОТНОЙ МОДУЛЯЦИИ

26

27. СПЕКТРЫ СИГНАЛОВ

Спектры ЧМ сигнала при
гармоническом
модулирующем сигнале
и при различных индексах
Мчм:
а) при Мчм=0,5,
б) при Мчм=1,
в) при Мчм=5.
27

28. 2 учебный вопрос ФОРМИРОВАНИЕ И ДЕТЕКТИРОВАНИЕ СИГНАЛОВ ПРИ ПЕРЕДАЧЕ ДИСКРЕТНЫХ СООБЩЕНИЙ

28

29. ЦИФРОВАЯ МОДУЛЯЦИЯ

Манипуляция (цифровая модуляция) — в теории передачи дискретных
сообщений процесс преобразования последовательности кодовых
символов в последовательность элементов сигнала (частный случай
модуляции — при дискретных уровнях модулирующего сигнала).
•Спектр амплитуд сигнала - сумма амплитуд гармонических колебаний,
определяющих этот сигнал.
•Составляющие спектра называются гармониками с частотами кратными
частоте сигнала.
•Спектр периодического сигнала дискретен по частоте и бесконечен.
Кратность обращения гармоник в ноль равна скважности периодического
сигнала.
•Скважность сигнала – отношение периода сигнала к длительности импульса.
•Спектр непериодического сигнала является непрерывным и бесконечным.
При этом говорят о спектральной плотности , которая показывает распределение
амплитуд по спектру.
29

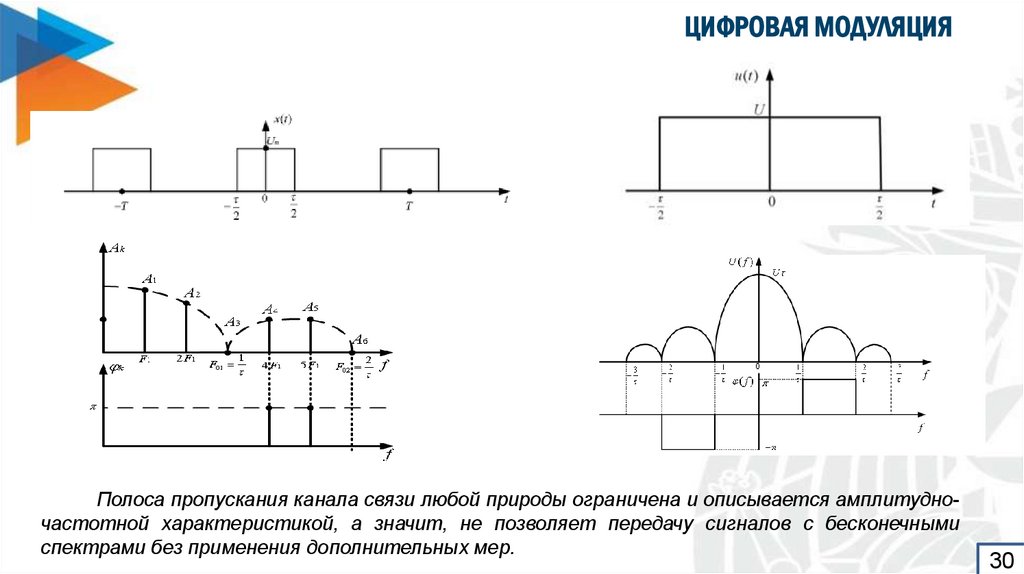
30. ЦИФРОВАЯ МОДУЛЯЦИЯ

Полоса пропускания канала связи любой природы ограничена и описывается амплитудночастотной характеристикой, а значит, не позволяет передачу сигналов с бесконечными
спектрами без применения дополнительных мер.
30

31. ЦИФРОВАЯ МОДУЛЯЦИЯ

Цифровая модуляция – это процесс изменения одного или нескольких
параметров несущего гармонического колебания по закону информационного
цифрового сигнала
Амплитудная манипуляция
Частотная манипуляция
Фазовая манипуляция
31

32. АМПЛИТУДНАЯ МАНИПУЛЯЦИЯ

Амплитудная манипуляция (Amplitude Switch Keying (ASK)
подразумевает скачкообразное изменение амплитуды несущего колебания
по закону информационного цифрового сигнала.
При амплитудной модуляции для логической единицы выбирается один
уровень амплитуды синусоиды несущей частоты, а для логического нуля —
другой.
Недостаток амплитудной манипуляции – низкая помехоустойчивость.
По этой причине ASK редко используется в чистом виде на практике, но
часто применяется в сочетании с другим видом модуляции — фазовой
модуляцией.
32

33. ЧАСТОТНАЯ МАНИПУЛЯЦИЯ

При частотной манипуляции (Frequency Switch Keying - FSK) значения
нуля и единицы исходных данных передаются синусоидами с различной
частотой — f1 и f2.
Достоинство: этот способ модуляции не требует сложных схем и обычно
применяется в низкоскоростных модемах, работающих на скоростях 300 и
1200 бит/с. При использовании только двух частот за один такт передается
один бит информации, поэтому такой способ называется двоичной
частотной манипуляцией (Binary FSK, BFSK).
Может также использоваться четыре различных частоты для кодирования
двух битов информации в одном такте, такой способ носит название
четырехуровневой частотной манипуляции (four-level FSK). Применяется
также название многоуровневая частотная манипуляция (Multilevel FSK,
MFSK).
33

34. ФАЗОВАЯ МАНИПУЛЯЦИЯ

При фазовой манипуляции (Phase Shift Keying - РSК ) значения нуля и
единицы исходных данных передаются синусоидами с различной фазой —
φ1 и φ2.
Недостаток – более сложная реализация,
достоинство – экономия частотного ресурса и обеспечение более
помехозащищенного информационного обмена.
В простейшем случае несущая может иметь два значения фазы - 0 и 180°.
34