Задача лінійного програмування та методи її розв’язування

1. Тема 2 Задача лінійного програмування та методи її розв’язування

2. 2.1. Постановка задач: загальна задача оптимального лінійного програмування та форми її запису

Загальна лінійна (всі змінні – х в першому степені)
математична модель економічних процесів і явищ – так
звана загальна задача лінійного програмування
подається у вигляді:
F c1 x1 c2 x2 ... cn xn max(min) (1)
a11 x1 a12 x2 .... a1n xn , , b1
a21 x1 a22 x2 .... a2 n xn , , b2
...................................................
a x a x .... a x , , b
m
mn n
m1 1 m 2 2
x1 0, x2 0,...., xn 0
(2)
(3)

3.

де с1,2….n – коефіцієнти цільової функції;
х1,2….n – змінні;
а1,2….m – коефіцієнти при змінних;
b1,2….m – вільні члени (ресурси, запаси).

4.

(!)
Потрібно знайти значення
змінних x1, x2, …, xn, які
задовольняють умови (2) і (3), тоді
як цільова функція набувала би
екстремального (максимального чи
мінімального) значення.

5.

Задачу (1) – (3) доцільно звести до канонічної форми,
тобто до такого вигляду, коли в системі обмежень (2):
всі bi (i = 1, 2, …, m) невід’ємні;
всі обмеження є рівностями.
1. Якщо якесь bi від’ємне, то, помноживши i-те
обмеження на (–1), дістанемо у правій частині
відповідної рівності додатне значення.
2. Коли i-те обмеження має вигляд нерівності
ai1 x1 ai 2 x2 .... ain xn bi ,
то останню завжди можна звести до рівності, увівши
додаткову змінну xn + 1: ai1 x1 ai 2 x2 .... ain xn xn 1 bi .
Аналогічно обмеження виду ak1 x1 ak 2 x2 .... akn xn bk
зводимо до рівності, віднімаючи від лівої частини
додаткову змінну хn + 2, тобто ak1 x1 ak 2 x2 .... akn xn xn 2 bk .

6. ПРИКЛАД

Записати в канонічній формі таку задачу лінійного
F 2 x1 3 x2 4 x3 max
програмування:
за умов x1 2 x2 3x3 10
x1 2 x2 3 x3 180
5 x x 2 x 100
3
1 2
.
x1 0, x2 0, x3 0
Розв’язування. Помножимо другу нерівність на (–1)
і введемо відповідно допоміжні змінні х4 і х5 для
другого та третього обмеження:
x1 2 x2 3x3 10
x1 2 x2 3x3 x4 180
5 x x 2 x x 100
3
5
1 2
x1 0, x2 0, x3 0, x4 0, x5 0.
Неважко переконатися, що допоміжні змінні, у цьому разі х4 і х5, є
невід’ємними, причому їх уведення не змінює цільової функції.

7.  Отже, будь-яку задачу лінійного програмування можна записати в такій канонічній формі:

Отже, будь-яку задачу лінійного
програмування можна записати в
такій канонічній формі:
F c1 x1 c2 x2
за умов
cn xn max (4)
a11 x1 a12 x2 a1n xn b1
a x a x a x b
21 1 22 2
2n n
2
.............................................
am1 x1 am 2 x2 amn xn bm
x1 0, x2 0,
, xn 0
(5)
(6)

8.

Задачу (4) – (6) можна розв’язувати на
мінімум, якщо цільову функцію
помножити на (–1), тобто:
max F min( F ) min( c1 x1 c2 x2
cn xn )

9. Основні поняття

Допустимий розв’язок або допустимий
план задачі – відображає вектор X ( x1 , x2 ,..., xn )
, координати якого задовольняють систему
обмежень (2) і (3).
a11 x1 a12 x2 .... a1n xn , , b1
a21 x1 a22 x2 .... a2 n xn , , b2
...................................................
a x a x .... a x , , b
m
mn n
m1 1 m 2 2
x1 0, x2 0,...., xn 0
(2)
(3)

10.

Сукупність допустимих розв’язків (планів) задачі
утворює область допустимих розв’язків задачі.
Опорним планом задачі лінійного програмування
називається допустимий план, який задовольняє не
менш ніж п лінійно незалежних обмежень системи
(2) у вигляді строгих рівностей разом з обмеженням
(3) щодо знака.
Опорний план називається невиродженим, якщо він
містить точно m додатних компонент. У противному разі
опорний план є виродженим.
Оптимальним розв’язком (планом) називається
той допустимий розв’язок, при якому лінійна
функція (1) набуває максимального (мінімального)
значення.

11. Запис задачі лінійного програмування

Задачу лінійного програмування (4-6)
зручно записувати за допомогою знака
суми « »:
n
max F c j x j
j 1
n
за умов a x
j 1
ij
j
bi
(i 1, 2,
, m);
x j 0 ( j 1, 2,
, n).
Запис задачі лінійного програмування у
векторно-матричному вигляді: max F CX
ext
АХ = B, Х ≥ 0
a11 , a12 ,
a , a22 ,
A aij 21
am1 , am 2
, a1n
, a2 n
, amn
b1
x1
b2
x
2
X
B
xn
bn

12. 2.2. Побудова економіко-математичних моделей задач лінійного програмування

2.2. Побудова економікоматематичних моделей задач
лінійного програмування
1 крок - З точки зору економіки, а не математики,
відповідаємо на такі питання:
Що є шуканими величинами задачі?
Якою є мета розв’язку? Який параметр задачі є
критерієм ефективності (оптимальності) розв’язку? У
якому напрямі повинно змінюватись значення цього
параметра для досягнення найкращих результатів?
Які умови у відношенні шуканих величин і ресурсів
задачі повинні бути виконані? Ці умови встановлюють,
як повинні співвідноситись один з одним різні
параметри задачі.

13.

2 крок – запис попередніх відповідей у математичній
формі. При цьому:
Шукані величини є змінними задачі, які, як правило,
позначають малими латинськими літерами з індексами.
Наприклад, однотипні змінні зручно подавати у вигляді
Мета розв’язку записується у вигляді цільової функції.
Яку позначають, наприклад
. Математична формула
цільової функції відображає спосіб розрахунку значень
параметра – критерію ефективності задачі.
Умови, які накладаються на змінні і ресурси задачі,
записують у вигляді системи рівностей або нерівностей,
тобто обмежень. Ліві і праві частини обмежень
відображають спосіб одержання (розрахунок або числові
значення з умови задачі) значень тих параметрів задачі, на
які були накладені відповідні обмеження.
В процесі запису математичної моделі необхідно
вказувати одиниці виміру змінних задачі, цільової функції і
всіх обмежень.

14. Приклади побудови лінійних математичних моделей

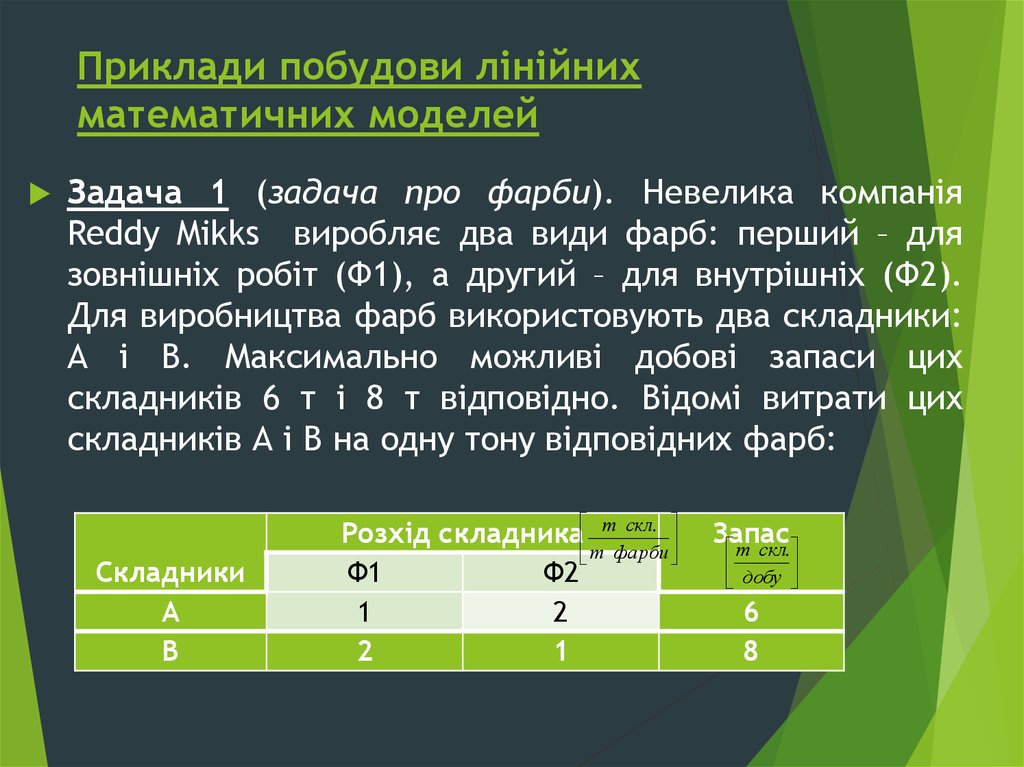
Задача 1 (задача про фарби). Невелика компанія
Reddy Mikks виробляє два види фарб: перший – для
зовнішніх робіт (Ф1), а другий – для внутрішніх (Ф2).
Для виробництва фарб використовують два складники:
А і В. Максимально можливі добові запаси цих
складників 6 т і 8 т відповідно. Відомі витрати цих
складників А і В на одну тону відповідних фарб:
Складники
А
В
Розхід складника т скл.
т фарби
Ф1
Ф2
1
2
2
1
Запас
т скл.
добу
6
8

15.

Після вивчення ринку збуту відділ маркетингу
компанії встановив, що добовий попит на фарбу
другого виду ніколи не перевищує попиту на фарбу
першого виду більше, ніж на 1 тону, а також
поставив умову, щоб добове виробництво фарби
другого виду не перевищувало 2 тон (у зв’язку з
відсутністю відповідного попиту). Оптові ціни
однієї тони фарби рівні 3 тис. грн. для Ф1, та 2
тис. грн. для Ф2. Компанія хотіла б визначити,
яким чином можна збільшити добовий дохід.
Необхідно:
Побудувати математичну модель задачі.
Встановити, яку кількість фарби кожного виду
необхідно виробляти, щоб дохід від реалізації
продукції був максимальним.

16. Побудова математичної моделі задачі

Шукані величини – добові об’єми виробництва
кожного виду фарби:
т Ф1
– фарби першого виду (Ф1) добу
Ф2
– фарби другого виду (Ф2) тдобу
Цільова функція – необхідно досягти максимуму
прибутку від реалізації продукції, отже, критерій
ефективності – параметр добового доходу, який
повинен прямувати до максимуму.
Оскільки оптові ціни на 1 тону фарб складають 2 і 3
тис. грн. відповідно, то:
дохід від продажу Ф1 рівний
дохід від продажу Ф2 рівний
3x1
2x1
тис.грн.
добу
тис.грн.
добу

17.

Тому цільова функція записується у вигляді суми
доходу від продажу Ф1 та Ф2:
F 3 x1 2 x2 max
тис. грн. т фарби тис. грн.
т фарби добу добу
Обмеження. Можливі об’єми виробництва фарб та
обмежуються такими умовами:
кількість складників А і В, що витрачаються за добу
на виробництво Ф1 та Ф2 не може перевищувати їх
добового запасу, тобто:
Розхід кожного складника Максимально можливий запас
на
виробництво
обох
видів
фарб
кожного складника
За умовою:
1 x1 2 x2 6 т скл. А( В) т фарби т скл. А( В)
2 x2 1 x2 8 т фарби
добу
добу

18.

обмеження по добовому об’єму виробництва Ф1 в
порівнянні з об’ємом виробництва Ф2:
Перевищення об ' єму
т фарби
виробництва
Ф
1
над
1
добу
об ' ємом виробництва Ф 2
т фарби
добу
т фарби
добу
За умовою:
обмеження по добовому виробництву фарби другого
виду:
т фарби
x2 x1 1
Попит
За умовою:
x2 2
на Ф 2 2
т фарби
добу
добу
т фарби
добу

19.

невід’ємність об’ємів виробництва:
x1 0
x2 0
Отже, математична модель задачі має вигляд:
F 3 x1 2 x2 max
x1 2 x2 6
2x x 8
1 2
x1 x2 1
x2 2

20.

Задача 2. Фірма спеціалізується на виробництві
офісних меблів, зокрема вона випускає два види
збірних книжкових полиць – А та В. Полиці обох видів
виготовляють на верстатах 1 та 2. Тривалість обробки
деталей однієї полиці кожної моделі подано в таблиці:
Верстат
1
2
Тривалість обробки
полиці моделі, хв.
А
30
12
В
15
26
Ресурс робочого часу
верстатів, год. на тиждень
40
36
Прибуток фірми від реалізації однієї полиці моделі А
дорівнює 50 у. о., а моделі В – 30 у. о. Вивчення ринку
збуту показало, що тижневий попит на книжкові полиці
моделі А ніколи не перевищує попиту на модель В
більш як на 30 одиниць, а продаж полиць моделі В не
перевищує 80 одиниць на тиждень.

21.

Необхідно:
Побудувати математичну модель
задачі.
Визначити обсяги виробництва
книжкових полиць цих двох моделей,
що максимізують прибуток фірми.

22. Побудова математичної моделі задачі

Шукані величини: х1 – кількість полиць моделі А,
виготовлених фірмою за тиждень, а х2 – кількість
полиць моделі В.
Цільова функція – максимум прибутку фірми від
реалізації продукції. Математично вона подається так:
F 50 x1 30 x2 max
Обмеження. Обмеження задачі враховують
тривалість роботи верстатів 1 та 2 для
виготовлення продукції та попит на полиці різних
моделей.

23.

Обмеження на тривалість роботи верстатів 1 та 2
мають вид:
для верстата 1:
30х1 + 15х2 ≤ 2400 (хв);
для верстата 2:
12х1 + 26х2 ≤ 2160 (хв).
Обмеження на попит записуються так:
х1 – х2 ≤ 30 та х2 ≤ 80.
Отже, економіко-математична модель задачі має
вигляд:
F 50 x1 30 x2 max
30 x1 15 x2 2400
12 x 26 x 2160
1
2
x1 x2 30
x2 80
x1 0
x2 0

24.

Задача 3. На ринок доставляється картопля з
трьох фермерських господарств по ціні
відповідно 80, 75, та 65 коп. за 1 кг. На
завантаження 1 т картоплі у фермерських
господарствах відповідно витрачається по 1,
6, 5 хвилин. Замовлено 12 т картоплі і для
своєчасної доставки необхідно, щоб на її
завантаження витрачалось не більше сорока
хвилин. Визначити з яких фермерських
господарств і в якій кількості необхідно
доставити картоплю, щоб загальна вартість
закупівлі
була
мінімальною,
якщо
господарства можуть виділити для продажу
відповідно 10, 8 та 6т картоплі.

25. Побудова математичної моделі

Позначимо x1– кількість картоплі, що буде закуплено у
першому господарстві (т); x2 , x3 – кількість картоплі
закупленої відповідно у другого та третього
господарства (т).
Зафіксуємо потрібну кількість поставок картоплі:
x1 x2 x3 12 ,
наступне обмеження описує витрати часу на
завантаження потрібної кількості продукції: x1 6 x2 5 x3 40,
враховуємо загальні обмеження по можливості поставок
продукції у кожному господарстві: x1 10, x2 8, x3 6.
Вартість закупленої продукції визначається, як сума
добутків ціни на кількість: F 80 x1 75 x2 65 x3 .

26.

Таким чином математична модель задачі має
вигляд:
F 80 x1 75 x2 65 x3
x1 x2 x3 12,
x 6 x 5 x 40,
2
3
1
x1 10,
x 8,
2
x3 6.
xi 0, i 1, 2,3

27. 2.3. Розв’язування задачі лінійного програмування симплекс-методом – самостійне вивчення

28. 2.4. Графічний метод розв’язування задачі лінійного програмування

Графічний метод є доволі простим і наочним
для розв’язування ЗЛП з двома змінними.
Він базується на геометричному
представленні допустимих розв’язків і
цільової функції.
Множина обмежень довільної ЗЛП є
множиною розв’язків деякої системи
лінійних рівнянь і нерівностей.
Спільною властивістю таких множин є
властивість опуклості.

29.

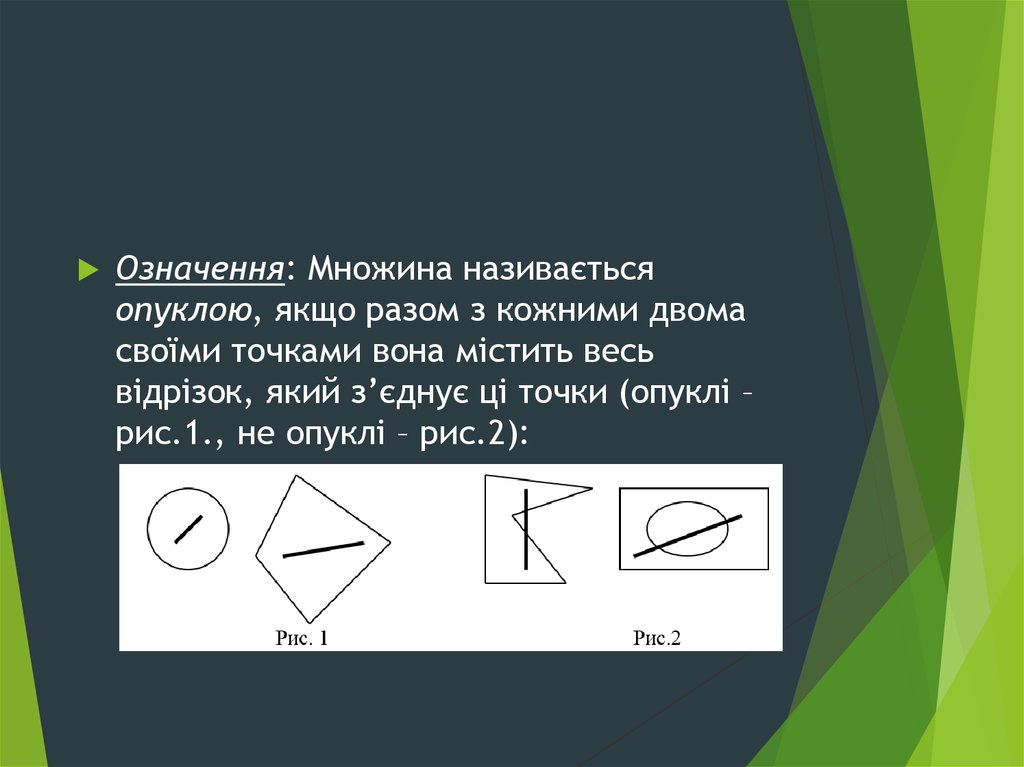
Означення: Множина називається
опуклою, якщо разом з кожними двома
своїми точками вона містить весь
відрізок, який з’єднує ці точки (опуклі –
рис.1., не опуклі – рис.2):

30. Нехай необхідно розв’язати ЗЛП з двома змінними:

F c1 x1 c2 x2 max(min)
за обмежень: a x a x b , x 0, x 0,
i1 1
i2 2
i
1
2
i 1,...m
a11 x1 a12 x2 b1 ,
Кожна нерівність a21 x1 a22 x2 b2 , цієї системи
..........................
am1 x1 am 2 x2 bm .
геометрично визначає в декартовій системі
координат х1Оx2 півплощину з граничною прямою
ai1 x1 ai 2 x2 bi (i = 1, 2, ...,т).
Умови невід’ємності визначають півплощини
відповідно з граничними прямими x1 0, x2 0
(тобто I-шу координатну чверть).

31.

Якщо система сумісна, то півплощини,
як опуклі множини, перетинаючись,
утворюють спільну частину, що є
опуклою множиною і називається
множиною обмежень М або областю
допустимих розв’язків

32. Припустимо, що множина обмежень є непорожньою множиною.

! ЗЛП полягає в тому, щоб серед усіх точок
множини М знайти таку, координати якої
надають max(min) значення цільовій функції
F c1 x1 c2 x2
Функція F при фіксованому значенні F ( X ) C
визначає на площині пряму c1 x1 c2 x2 C ( LC )
Змінюючи значення C ми одержимо сім’ю
паралельних прямих, які називають лініями
рівня. При цьому, для розв’язування достатньо
побудувати одну із них, довільно вибравши
значення C.
зручно брати С= НСК (c1 , c2 )

33.

Напрям зростання значення цільової функції
задачі задає вектор
N gradC
F
F
i
j c1i c2 j (c1 ; c2 )
x1
x2
який є перпендикулярним до кожної з ліній
рівня.
! Напрям вектора N співпадає з напрямом
зростання цільової функції, а напрям спадання
цільової функції є напрямом, протилежним до
напряму вектора N .

34. Суть графічного методу полягає в наступному:

! за напрямом (або проти напряму) вектора N в
області допустимих розв’язків M здійснити
пошук оптимальної точки X ( x1 ; x2 )
Оптимальною вважається та точка, через яку
проходить лінія рівня Fmax ( Fmin ) , яка відповідає
найбільшому (найменшому) значенню функції F.
Оптимальний розв’язок завжди знаходиться
на межі області допустимих розвязків,
наприклад, в останній вершині многокутника
допустимих розвязків, через яку проходить
цільова пряма або на всій його стороні.

35.

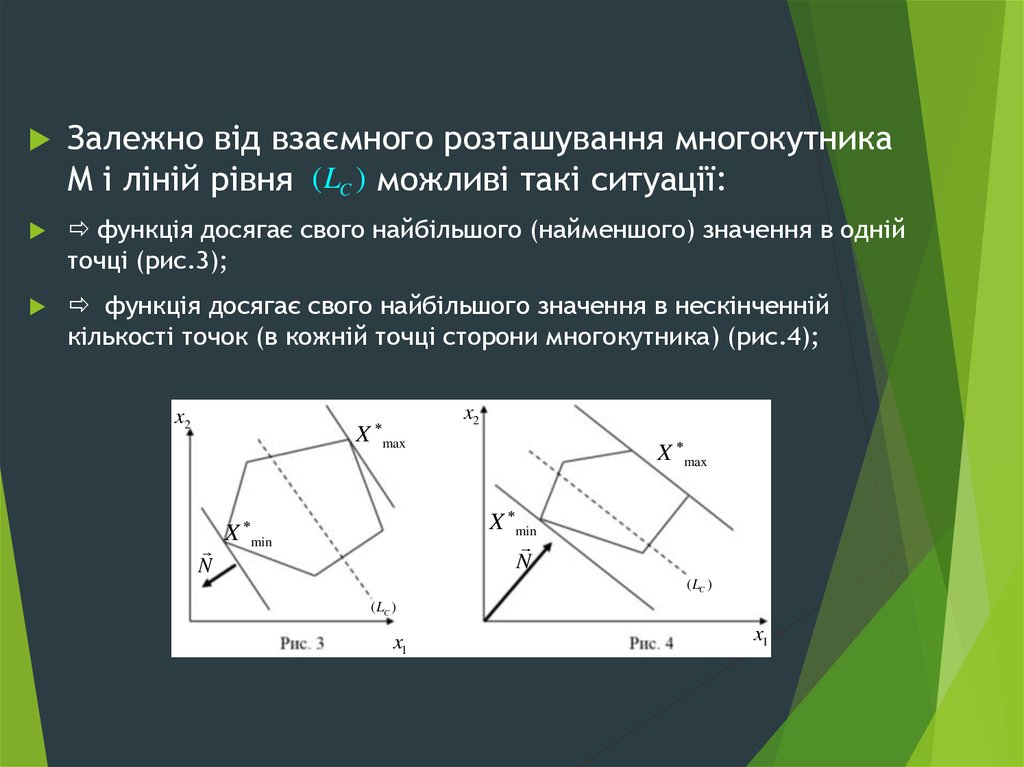
Залежно від взаємного розташування многокутника
М і ліній рівня ( LC ) можливі такі ситуації:
функція досягає свого найбільшого (найменшого) значення в одній
точці (рис.3);
функція досягає свого найбільшого значення в нескінченній
кількості точок (в кожній точці сторони многокутника) (рис.4);
x2
X
x2
X max
max
X min
X min
N
N
( LC )
( LC )
x1
x1

36.

Якщо ж множина М необмежена, то можливі
такі ситуації:
функція F обмежена зверху, але необмежена знизу на
множині M (у цьому випадку ЗЛП на знаходження найбільшого
значення має розв’язок, а на знаходження найменшого – ні)
(рис.5);
функція F обмежена знизу, але необмежена зверху на
множині M (у цьому випадку ЗЛП на знаходження найменшого
значення має розв’язок, а на знаходження найбільшого – ні)
(рис.6).
x2
x2
Fmin
Fmin
X min
X max
N
N
( LC )
( LC )
x1
x1

37. Властивості розв’язків задачі лінійного програмування формулюються у вигляді чотирьох теорем.

Властивість 1. (Теорема 1.) Множина всіх планів
задачі лінійного програмування опукла.
Властивість 2. (Теорема 2.) Якщо задача
лінійного програмування має оптимальний план, то
екстремального значення цільова функція набуває
в одній із вершин многогранника розв’язків. Якщо
цільова функція набуває екстремального значення
більш як в одній вершині цього многогранника, то
вона досягає його і в будь-який точці, що є
лінійною комбінацією таких вершин.

38.

Властивість 3. (Теорема 3.) Якщо відомо, що
система векторів A1 , A2 ,..., Ak (k n) у розкладі
A1 x1 A2 x2 ... An xn A0
A1 x1 A2 x2 ... Ak xk A0
, X 0 лінійно незалежна і така, що
, де всі x j 0 , то точка X ( x1 , x2 ,..., xk , 0,..., 0)
є кутовою точкою багатогранника розв’язків.
Властивість 4. (Теорема 4.) Якщо X ( x1 , x2 ,..., xn )
– кутова точка багатогранника розв’язків, то
вектори в розкладі A1 x1 A2 x2 ... An xn A0 , X 0,
що відповідають додатнім x j є лінійно
незалежними.

39. З наведених властивостей випливає:

Якщо функціонал задачі лінійного програмування
обмежений на багатограннику розв’язків, то:
існує така кутова точка багатогранника розв’язків,
в якій лінійний функціонал досягає свого
оптимального значення;
кожний опорний план відповідає кутовій точці
багатогранника розв’язків. Тому, для розв’язання
задачі лінійного програмування необхідно
досліджувати лише кутові точки багатогранника
(опорні плани), не включаючи до розгляду внутрішні
точки множини допустимих планів.

40. Приклад 1.

Розглянемо графічний метод розв’язування
задачі про фарби, математична модель якої
має вигляд (див. п. 1.3):
F 3 x1 2 x2 max
x1 2 x2 6
2x x 8
x1 0
1 2
x1 x2 1 x2 0
x2 2
Послідовність дій:
Будуємо прямі обмежень.
Спочатку замінюємо знаки нерівностей на знаки точних
рівностей.
x
y
Для побудови прямих зручно скористатись рівнянням a b 1 –
прямої у відрізках на координатних осях.
y
b
Далі нумеруємо, а потім і будуємо прямі .
a
0
x

41.

Прямі обмежень нашої задачі:
x1 x2
(1)
6 3 1
x1 x2 1 (2)
4 8
x1 x2
1 (3)
1 1
x2 2
4
Визначаємо і заштриховуємо півплощини,
які визначаються нерівностями.
Для цього в кожну нерівність підставляємо координати
контрольної точки, наприклад, точки (0;0) і перевіряємо, чи є
правильною одержана числова нерівність. Якщо нерівність вірна,
то заштриховуємо півплощину, яка містить точку (0;0) , якщо ж
нерівність невірна, то заштрихувати півплощину, яка не містить
контрольну точку.
В результаті маємо:
(1) (0;0) 0 6
(2) (0;0) 0 8
(3) (0;0) 0 1
(4) (0;0) 0 2

42.

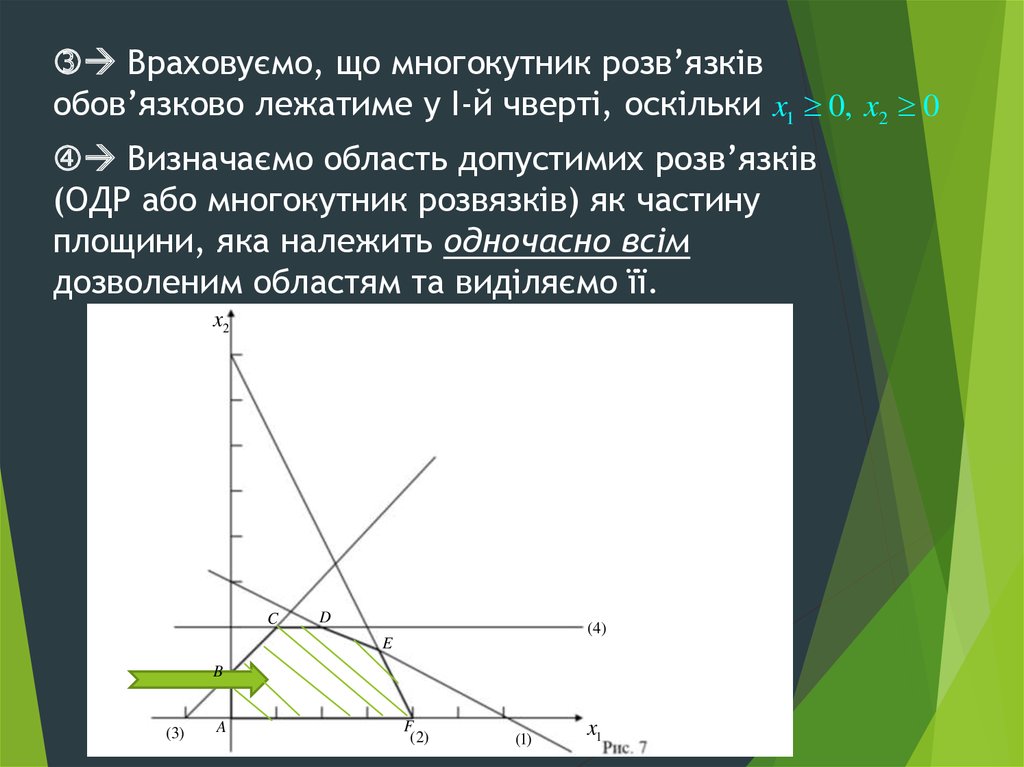
Враховуємо, що многокутник розв’язків
обов’язково лежатиме у I-й чверті, оскільки x1 0, x2 0
Визначаємо область допустимих розв’язків
(ОДР або многокутник розвязків) як частину
площини, яка належить одночасно всім
дозволеним областям та виділяємо її.
x2
C
D
(4)
E
B
(3)
A
F
(2)
(1)
x1

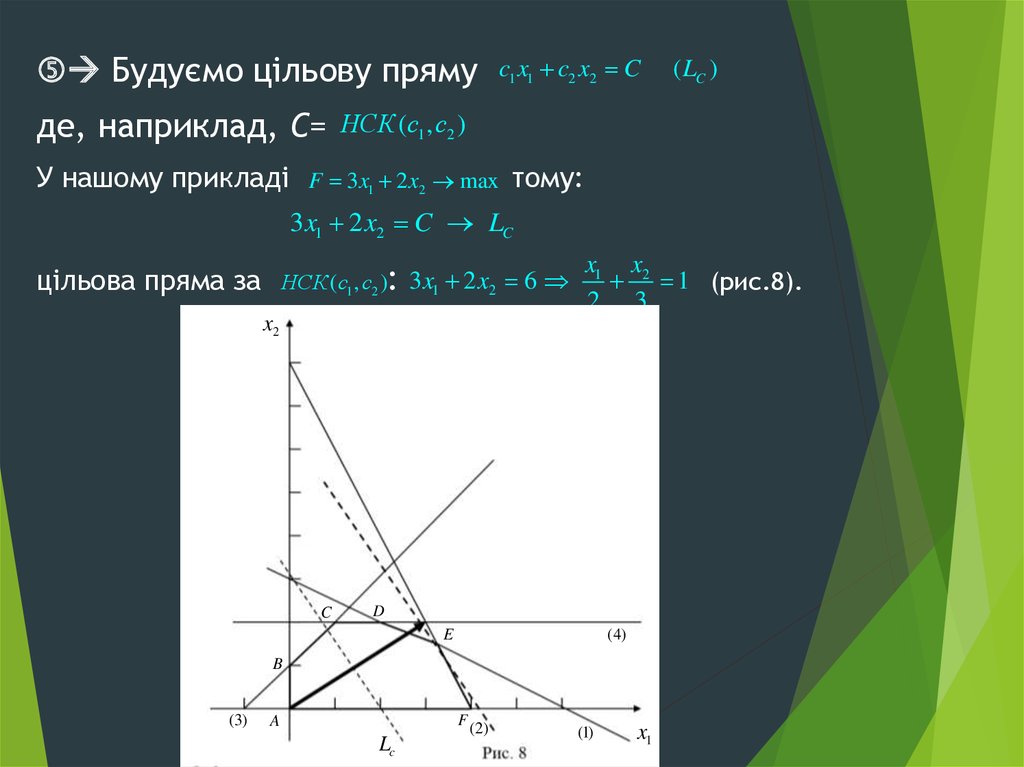
43.

Будуємо цільову пряму
де, наприклад, С=
У нашому прикладі
c1 x1 c2 x2 C
( LC )
НСК (c1 , c2 )
F 3 x1 2 x2 max
тому:
3 x1 2 x2 C LC
НСК (c1 , c2 ): 3 x1 2 x2 6
цільова пряма за
x1 x2
1 (рис.8).
2 3
x2
C
D
(4)
E
B
(3)
A
Lc
F (2)
(1)
x1

44.

Будуємо вектор-градієнт: N gradC c1i c2 j (c1 ; c2 )
з початком в точці
(0;0)
У нашому прикладі N 3i 2 j
N 3i 2 j
Шукаємо максимум цільової функції, переміщаючи
пряму LC у напрямі вектора N , при пошуку мінімуму –
у напрямі, протилежному до напряму вектора N .
Остання по ходу руху вершина многокутника буде
відповідно точкою максимуму або мінімуму.
Якщо точки не існує, то йде мова про необмеженість планів ЗЛП.

45.

У нашому прикладі точка Е буде останньою вершиною
багатокутника допустимих розв’язків ABCDEF через яку проходить
цільова пряма LC 3x1 2 x2 6 рухаючись у напрямі вектора N .
Отже, це точка максимуму цільової функції.
Визначаємо координати точки, в якій функція
досягає свого оптимуму X ( x1 ; x2 ) .
Для цього розв’язуємо систему рівнянь прямих, на перетині яких
знаходиться дана точка.
У нашому прикладі точка Е знаходиться на перетині прямих
(1) та (2):
x1 2 x2 6
10
4
x1 , x2
3
3
2 x1 x2 8
Знайти максимальне та (або) мінімальне значення
цільової функції:
Fmax ( Fmin ) c1 x1 c2 x2

46.

У нашому прикладі максимальне значення цільової функції:
Fmax F ( x1 ; x2 ) 3
10
4 38
2
3
3 3
тис. грн.
добу
Висновок: Найкращим режимом роботи фабрики є добове
виробництво фарби для зовнішніх робіт (Ф1) в об’ємі 10 т і
4
3
фарби для внутрішніх робіт (Ф2) в об’ємі 3 т.
При цьому дохід від продажу становитиме 38 тисяч гривень за добу.
3