Похожие презентации:
Післяоптимізаційний аналіз задач лінійного програмування
1. ЛЕКЦІЯ 7 - ПІСЛЯОПТИМІЗАЦІЙНИЙ АНАЛІЗ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ
ЛЕКЦІЯ 7 ПІСЛЯОПТИМІЗАЦІЙНИЙАНАЛІЗ ЗАДАЧ
ЛІНІЙНОГО
ПРОГРАМУВАННЯ
2. План
7.1 Аналіз коефіцієнтів лінійних моделей:аналіз коефіцієнтів цільової функції.
7.2 Аналіз діапазону зміни компонент
вектора обмежень.
7.3 Практичне використання двоїстих
оцінок у аналізі економічної задачі
(самостійна робота).
3.
max F c1 x1 c 2 x 2 ... c n x na11 x1 a12 x 2 ... a1n x n b1 ;
a x a x ... a x b ;
21 1
22 2
2n n
2
.......................................
a m1 x1 a m 2 x 2 ... a mn x n bm .
x j 0, j 1, n,
7.1
7.2
7.3
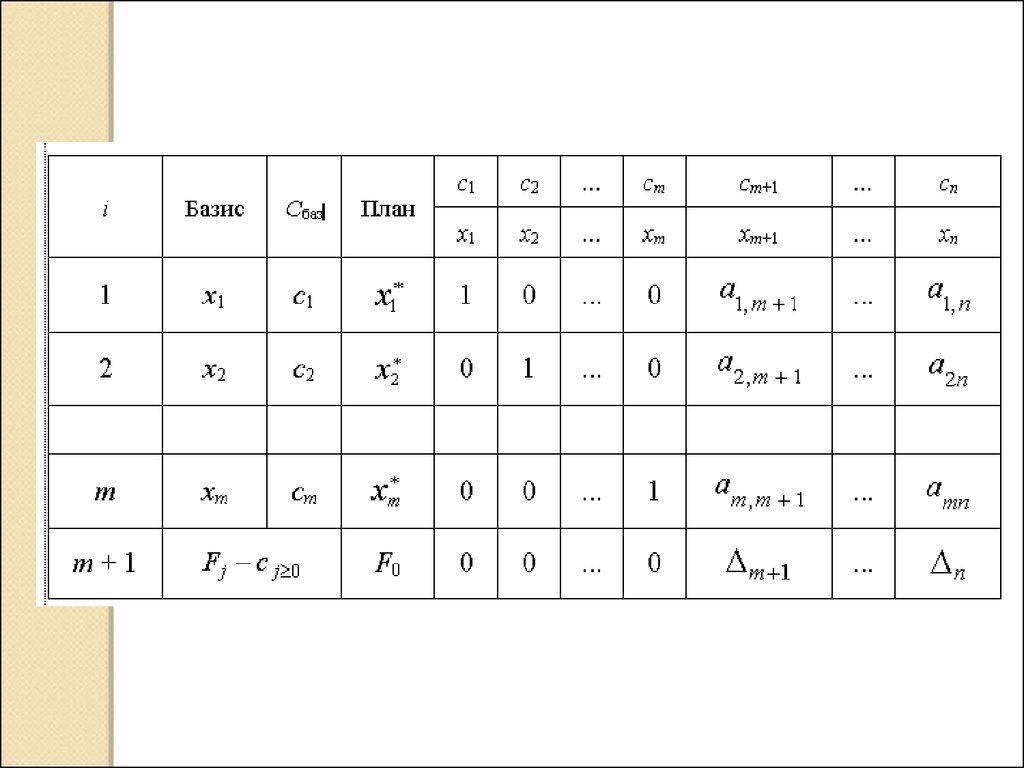
4.
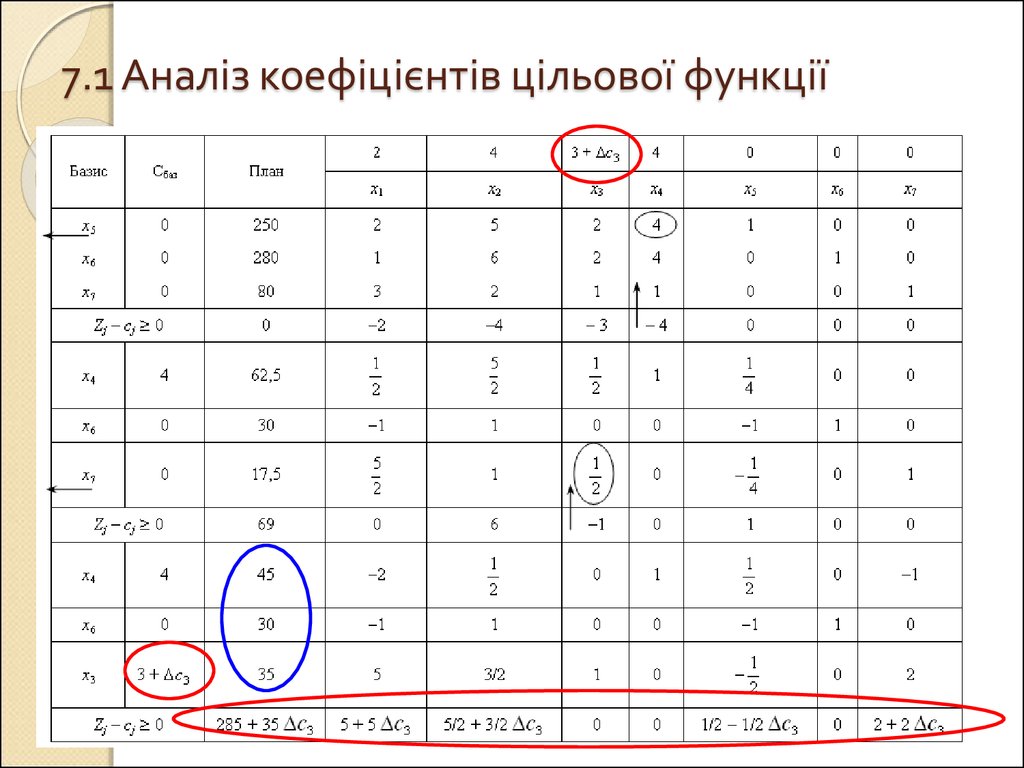
5. 7.1 Аналіз коефіцієнтів цільової функції
6.
Для базисних змінних(F1–c1) = 4 (–2) + 0 (–1) +(3 + c3) 5 – 2
= 5 + 5 c3;
(F2–c2) = 4 1/2 + 0 1 + (3 + c3) 3/2 – 4
= 5/2 + 3/2 c3;
(F5–c5) = 4 1/2 + 0 (–1)+ (3 + c3) · (–
1/2 )– 0 = 1/2 – 1/2 c3;
(F7–c7) = 4 (–1) + 0 0 + (3 + c3) · 2 – 0
= 2 + 2 c3
7. Zj – cj 0
Zj – cj 05 5 C 3 0;
5 / 2 3 / 2 C 0;
3
1
/
2
1
/
2
C
0
;
3
2 2 C 3 0 ;
C 3
C
3
C
3
C 3
1 C 3 1
2 C3 4
1;
5 / 3 ;
1;
1;
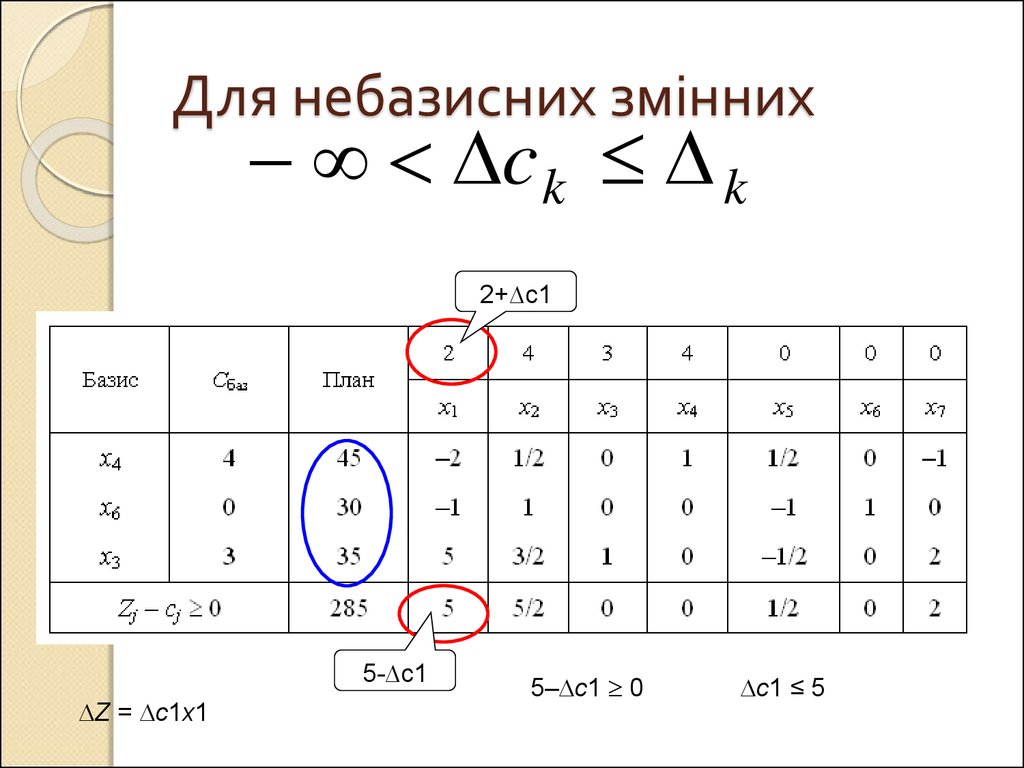
8. Для небазисних змінних
c k k2+∆с1
5-∆с1
Z = c1х1
5– c1 0
c1 ≤ 5
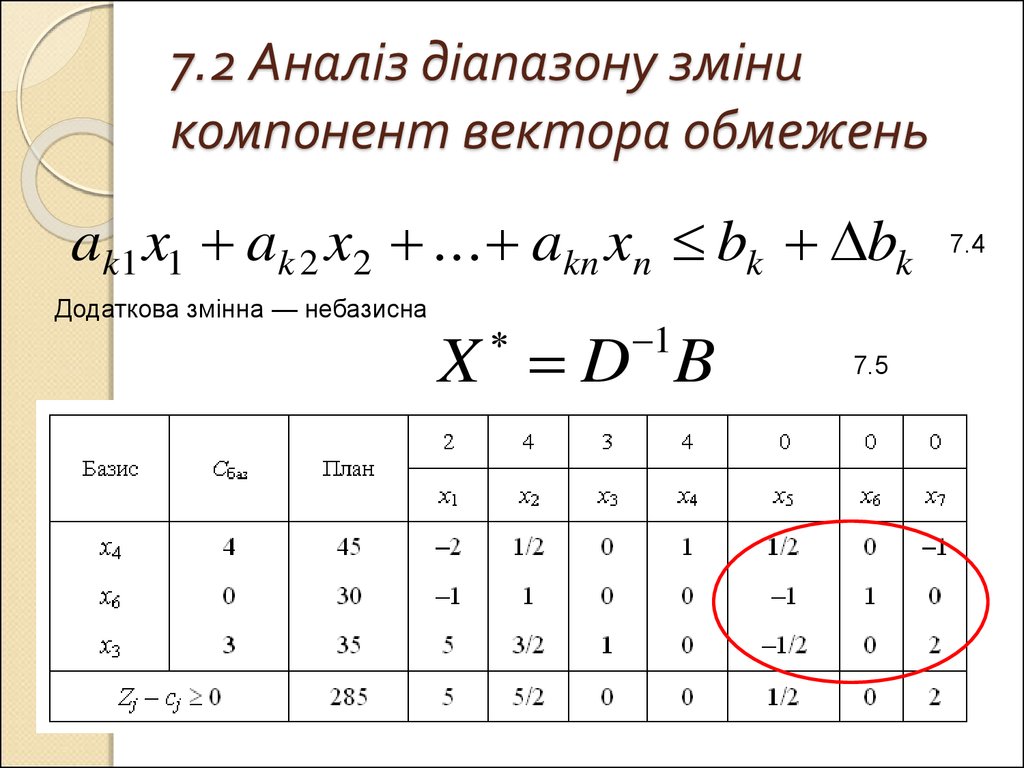
9. 7.2 Аналіз діапазону зміни компонент вектора обмежень
ak1 x1 ak 2 x2 ... akn xn bk bkДодаткова змінна — небазисна
1
X D B
7.5
7.4
10.
B B bk ek7.6
X D B D B bk D ek
1
1
1
X bk d k
7.7
a1,n k , a2,n k ,...,am,n k
X X bk d k
i
x ai , n k bk (i 1, m).
11.
12.
ix ai , n k bk 0 i 1, m.
7.8
xi
xi
max
bk min
a i ,n k 0 a
a i ,n k 0 a
i
,
n
k
i,n k
xi
bk bk max
a i ,n k 0 a
i,n k
7.9
xi
bk bk min
.
a i ,n k 0 a
i,n k
13.
nakj x j bk bk
j 1
n
akj x j (bk bk )
j 1
bk bk bk
14. Додаткова змінна — базисна
X D 1 B D 1 B bk D 1ekX bk d k
xi ai , n k bk 0 i 1, m.
7.8
7.7
x 0;
x 0;
.................
*
x
b
0
;
n
k
k
................
x * 0.
m
*
1
*
2
15.
n kx
bk
bk x
*
n k
7.10
,
7.11
xi
xi
max
bk min
a
0
a i ,n k 0 a
i ,n k
i,n k
ai , n k
7.9
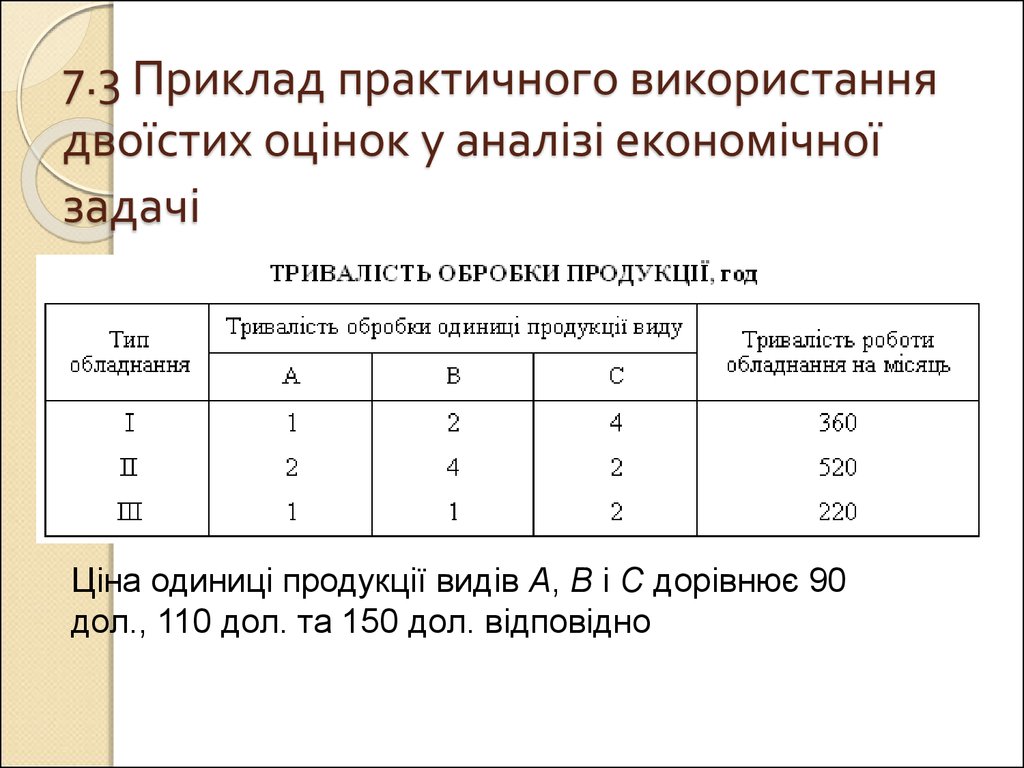
16. 7.3 Приклад практичного використання двоїстих оцінок у аналізі економічної задачі
Ціна одиниці продукції видів А, В і С дорівнює 90дол., 110 дол. та 150 дол. відповідно
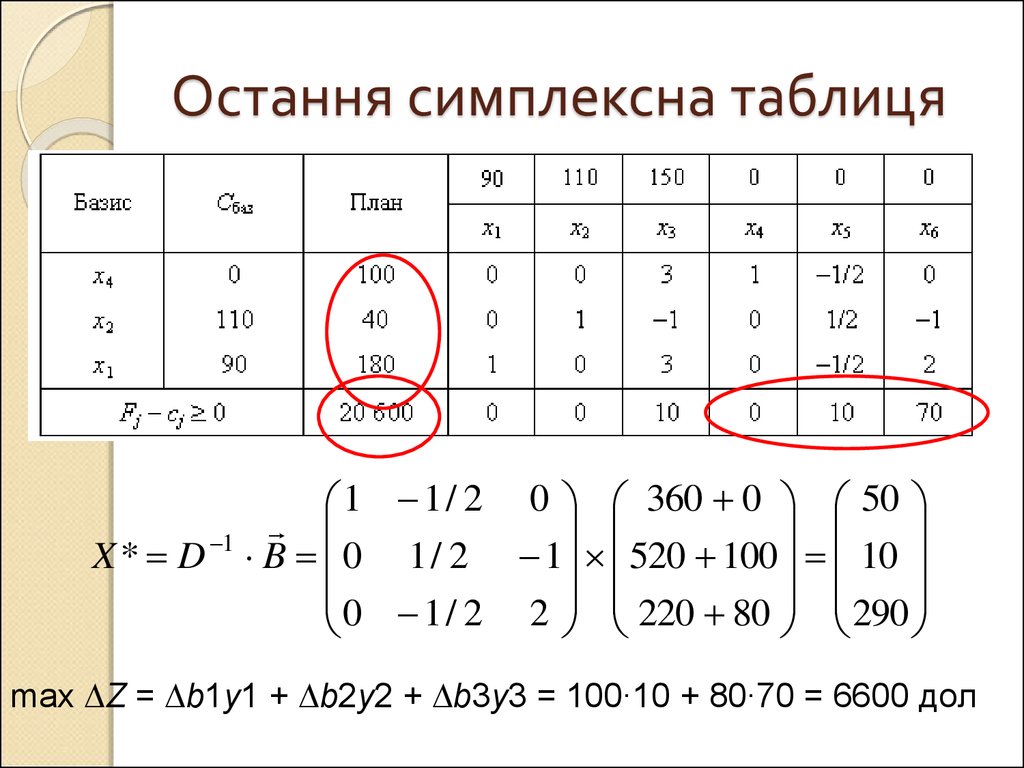
17. Остання симплексна таблиця
1 1 / 2 0 360 0 501
X * D B 0 1 / 2 1 520 100 10
0 1 / 2 2 220 80 290
max Z = b1y1 + b2y2 + b3y3 = 100∙10 + 80∙70 = 6600 дол
18.
110-25∆с2=-25
10+25
10-12,5
70+25


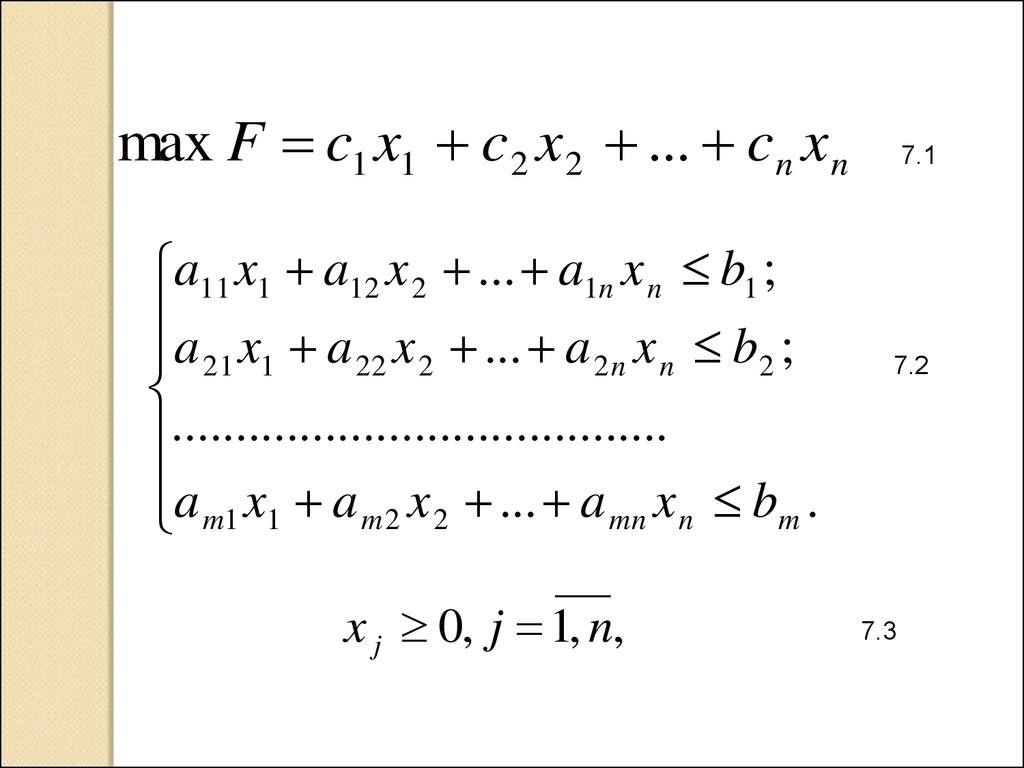

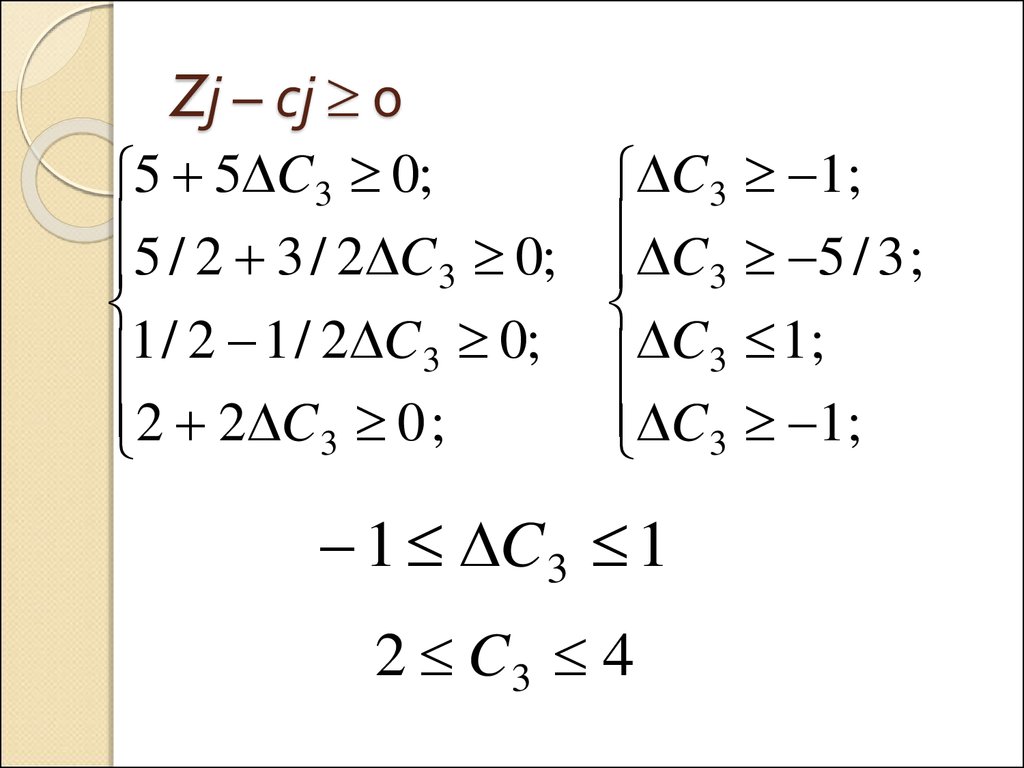



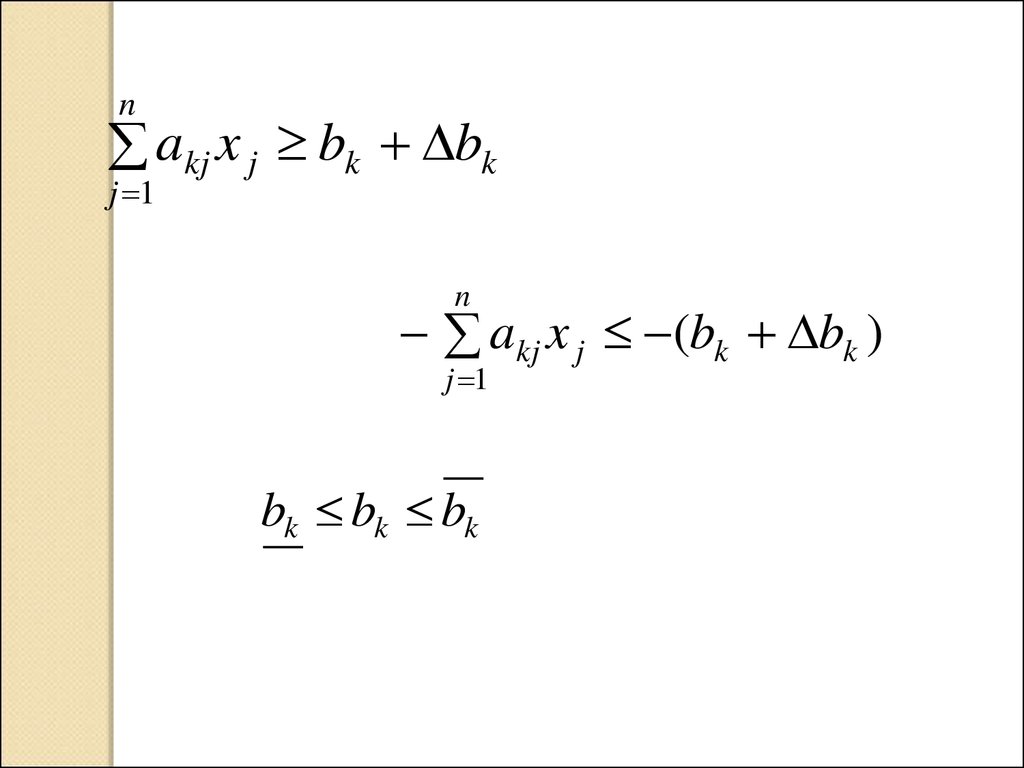



 Математика
Математика








