Функция у = cosx, ее свойства и график

1.  

2.

II Построение графика функции y = cosx с
применением тригонометрического круга
p - шесть клеток
p
2p
5p 3
2
3
6
II
Ось
p
y
p
I
p
6
косинусов
III
-1
-5p
6 -2p
3
-p
2
1
0
IY p
-p 6
3
0
1
-p
2
-p
p
-p
6
-5p -2p
3
6
-p
3
III
IY
0
-1
p x
2
p
p
6
3
I
2p
3
5p
6
II

3.

y
1
x
0
-1

4.

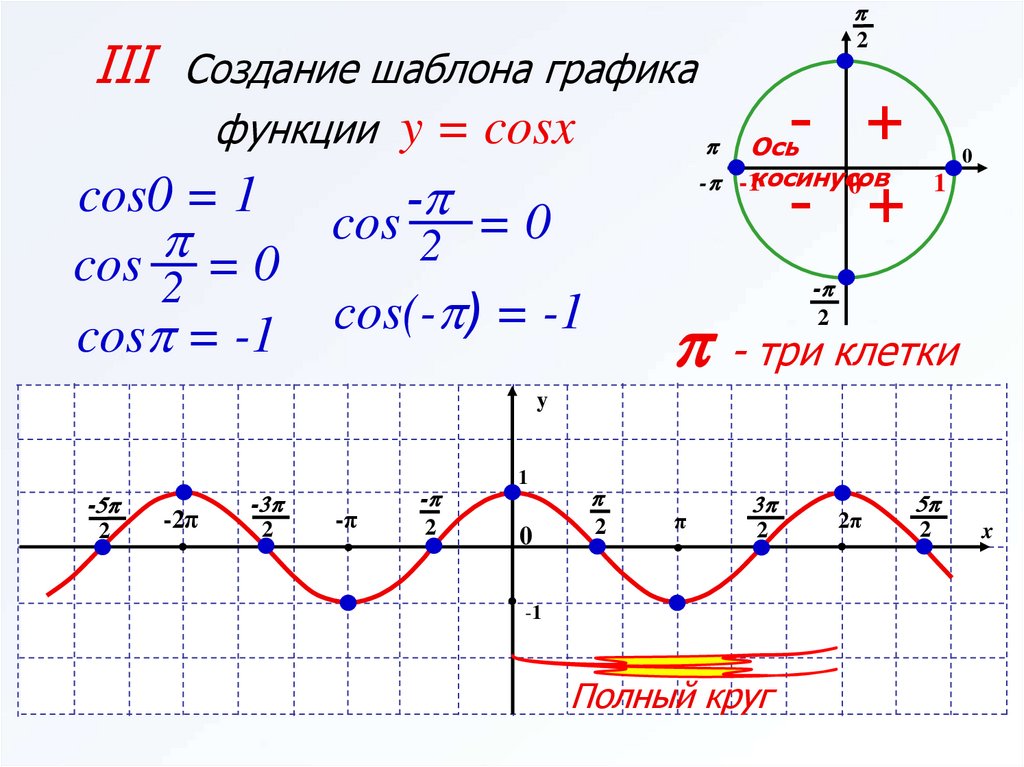
p
III Создание шаблона графика
функции y = cosx
cos0 = 1
p
cos 2 = 0
cosp = -1
2
- +
- +
Ось
-p -1косинусов
0
p
-p
cos 2 = 0
0
1
-p
2
сos(-p) = -1
p - три клетки
y
-5p
2
-2π
-3p
2
-π
-p
2
1
0
p
2
π
3p
2
-1
Полный круг
2π
5p
2
x

5.

y
1
x
0
-1

6. Основные свойства функции y=cosx

1. D ( у) R
2 . E ( у ) 1;1
3 . П ер и о д и ч ес к а я с п ер и о д о м 2 π : co s( x 2 π ) co s x
4 .Ч е т н а я : c o s( x ) c o s x
π
5. Н ули ф ун кц и и : cos х 0 п ри х π n ,n Z
2
π
π
6 . Промежутки знакопосто янства : cos x 0 на 2 π n ; 2 π n , n Z ;
2
2
3π
π
cos x 0 на 2 π n ; 2 π n , n Z
2
2
7 . Н а и б о л ь ш е е зн а ч е н и е у 1 п р и х 2 π n , n Z
Н а и м е н ь ш е е зн а ч е н и е у 1 п р и х π 2 π n , n Z
8 . Возраст ает на p 2p n ; 2p 2p n , n Z .
У бы вает на 2p n ; p 2p n , n Z

7. Построение графика функции y=cosx

у
у cos x
1
3
3π
2
–p
π
2
0
–1
π
π
ππ
6
4
32
p
3π
2
х
2p

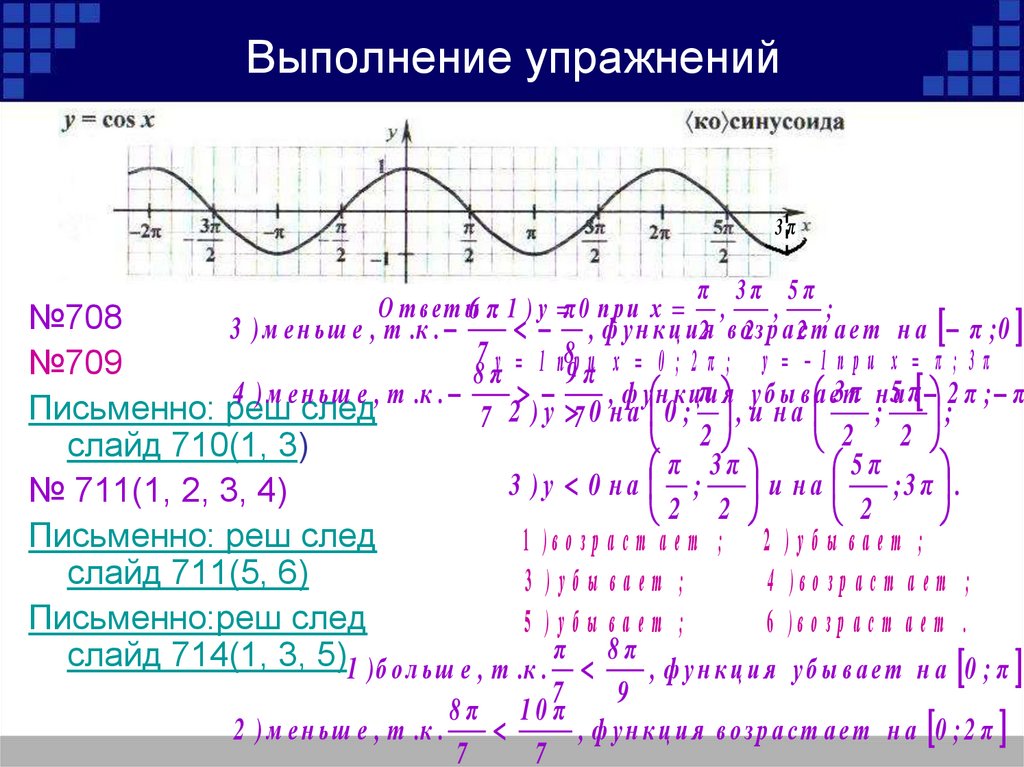
8. Домашнее задание п40, №712(1), №713(1)

9. Выполнение упражнений

3π
π 3π 5π
,
,
;
3 ) м е н ь ш е , т .к .
, ф у н к ц и2я в о2 зр а 2с т а е т н а π ; 0
7 у 1 п8р и х 0 ; 2 π ; у 1 п р и х π ; 3 π
8π
9π
О т в е т ы6 π: 1 ) у π 0 п р и х
№708
№709
4 ) м е н ь ш е , т .к .
, ф у н к цπи я у б ы в а е3тπ н 5а π 2 π ; π
Письменно: реш
след
;
;
7 2 ) у 7 0 н а 0 ; , и н а
2
2 2
слайд 710(1, 3)
π 3π
5π
3
)
у
0
н
а
;
и
н
а
;
3
π
.
№ 711(1, 2, 3, 4)
2 2
2
Письменно: реш след
1 )в о з р а с т а е т ; 2 ) у б ы в а е т ;
слайд 711(5, 6)
3 )убы вает ;
4 )в о з р а с т а е т ;
Письменно:реш след
5 )убы вает ;
6 )в о з р а с т а е т .
слайд 714(1, 3, 5)1 ) б о л ь ш е , т .к . π 8 π , ф у н к ц и я у б ы в а е т н а 0 ; π
7
9
8 π 10 π
2 ) м е н ь ш е , т .к .
, ф у н к ц и я в о зр а с т а е т н а 0 ; 2 π
7
7

10. Решение

710(1, 3)
3π π
1 ) π ; и ; π ;
2 2
3π
3 ) π ; и 0 ; π .
2
711(5, 6)
5 ) c o s 1 c o s 3 , т .к . 1 3 , y c o s x у б ы в а е т н а 0 ; π
6 ) c o s 4 c o s 5 , т .к . 4 5 , y c o s x в о з р а с т а е т н а π ; 2 π

11.

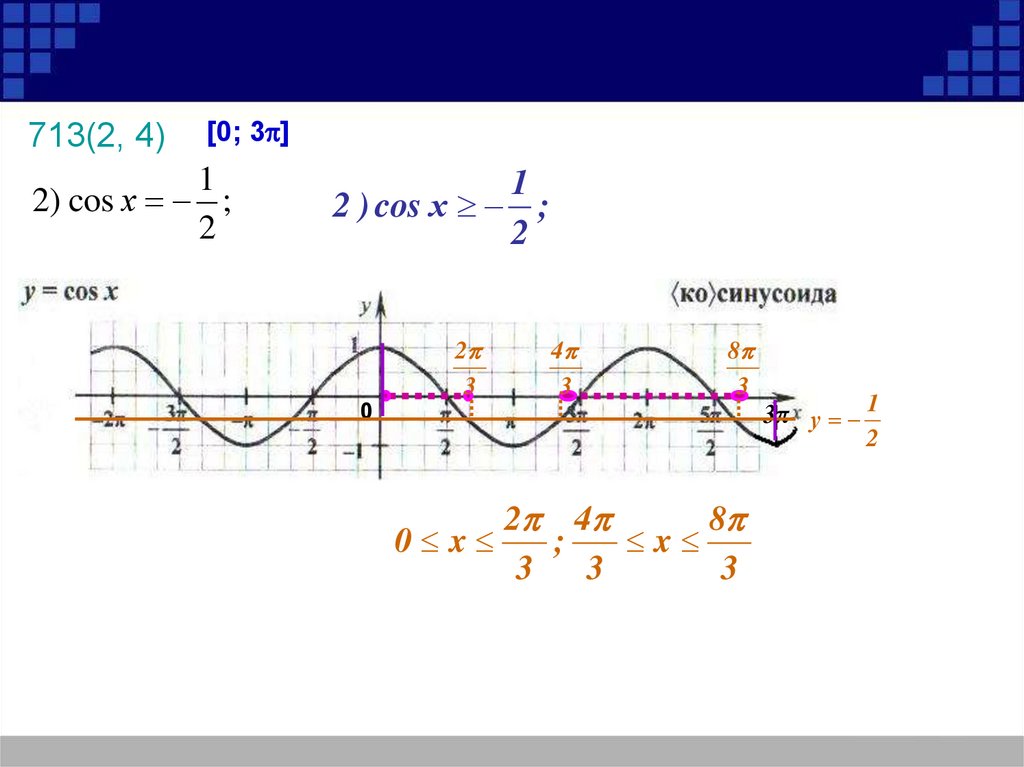
713(2, 4)
[0; 3p]
1
2) cos х ;
2
1
2 ) cos х ;
2
2p
3
4p
3
8p
3
0
3π у 1
2
0 x
2p 4p
8p
;
x
3
3
3

12. Решение

714(1, 3, 5)
π
3π
π π
1 ) sin cos cos
,
5
10
2 5
π
3π
π 3π
π
cos cos
, т .к .
и y cos x убывает на 0 ;
5
10
5 10
2
π
π
значит , cos sin .
π
π
5
5
О твет : cos sin .
5
5
5π
π
π 5π
π
3 ) sin
cos
cos cos ,
8
8
2 8
8
3p
p
3p p
cos
cos , т .к .
и y cos x убывает на 0; p
8
8
8
8
3p
5p
значит , cos
sin
.
3p
5p
8
8
Ответ : cos
sin
.
8
8

13. Решение

714(1, 3, 5)
5π
2π
π
π 5π
5 ) sin
cos
cos ,
cos
14
14
7
2 14
π
π
π π
π
cos cos , т .к . и y cos x убывает на 0 ;
6
7
6 7
2
π
5π
значит , cos sin
.
π
5π
6
14
О твет : cos sin
.
6
14

14. Домашнее задание №713(1),714(2,4,6)