Похожие презентации:
Полнота в логике высказываний
1.
Полнота в логикевысказываний
Лектор: Завьялов Олег Геннадьевич
кандидат физико-математических наук, доцент
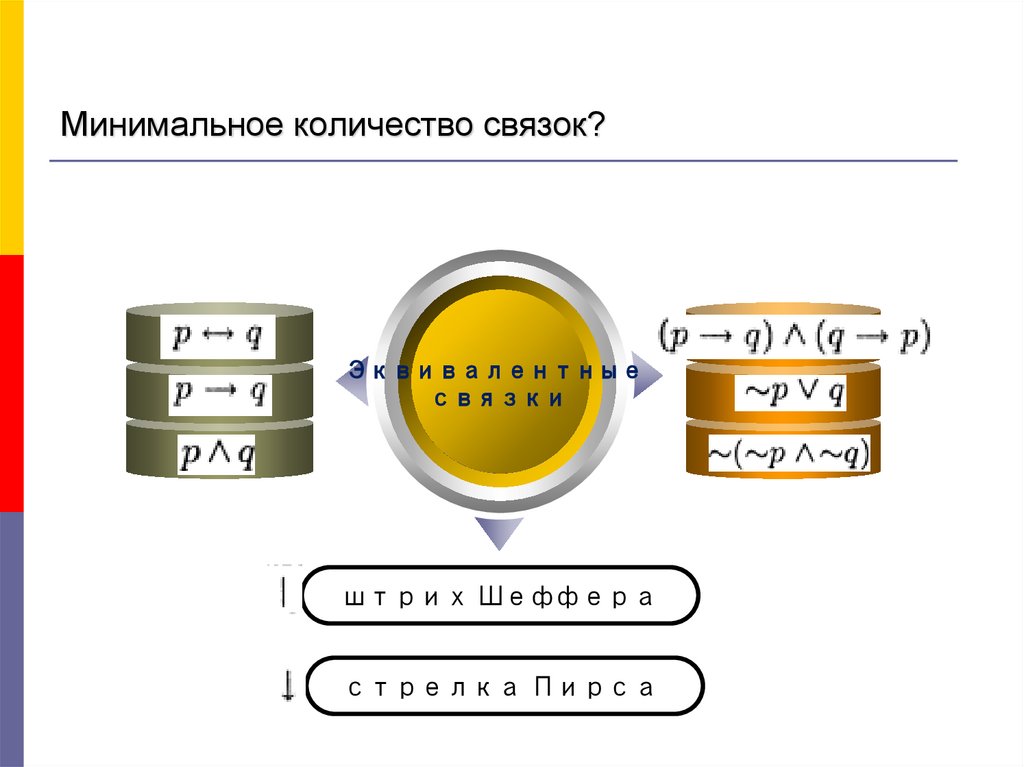
2. Минимальное количество связок?
TextЭквивалентные
связки
штрих Шеффера
стрелка Пирса
3.
Таблица истинности для связокШтрих Шеффера
1
2
3
4
1
1
0
0
1
0
1
0
Стрелка Пирса
0
1
1
1
1
2
3
4
1
1
0
0
1
0
1
0
0
0
0
1
4. Эквивалентные связки
Связка-не и
-не или
5.
Имеется таблица истинности1
2
3
4
1
1
0
0
1
0
1
0
Высказывание
задает таблицу истинности выше.
1
1
0
1
6.
Имеется таблица истинности для 3-х переменных1
2
3
4
5
6
7
8
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
Каждый случай задается своей конъюнкцией переменных.
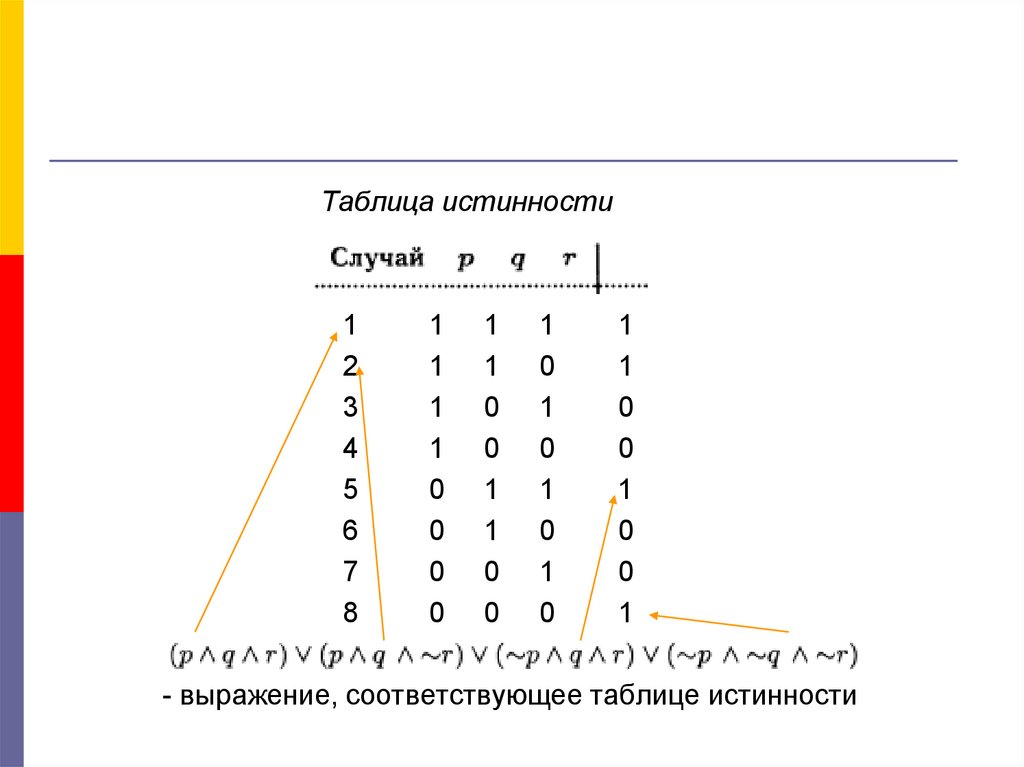
7.
Таблица истинности1
2
3
4
5
6
7
8
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
0
1
- выражение, соответствующее таблице истинности
8.
Таблица истинности1
2
3
4
5
6
7
8
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
1
1
0
0
1
0
0
- дизъюнктивная нормальная форма.
9. ДНФ
Пусть- простые высказывания.
Выражение
,
в котором
называется элементарной конъюнкцией.
Выражение, представляющее собой дизъюнкцию элементарных
конъюнкций, называется дизъюнктивной нормальной
формой (ДНФ).
Если m1, m2, m3, … , mn - элементарные конъюнкции,
тогда m1 v m2 v m3 v … v mn есть дизъюнктивная нормальная
форма.
10. СДНФ
Совершенная дизъюнктивная нормальная форма (СДНФ) – эточастный случай ДНФ, который удовлетворяет 3-м условиям:
в ней нет одинаковых слагаемых (элементарных конъюнкций);
в каждом слагаемом нет повторяющихся переменных;
каждое слагаемое содержит все переменные, от которых зависит
булева функция (каждая переменная может входить в слагаемое
либо в прямой, либо в инверсной форме).
Значение СДНФ состоит в том, что
для каждой конкретной функции её СДНФ единственна и однозначна;
СДНФ имеет однозначное соответствие с таблицей истинности функции.
Каждое слагаемое СДНФ соответствует одной строке в таблице истинности,
где функция =1. Число слагаемых в СДНФ равно числу единичных значений,
которые принимает булева функция в своей области определения;
СДНФ элементарно получается из таблицы истинноcти функции;
СДНФ удобна в качестве базового выражения для минимизации функции, в
ней особенно просто находятся слагаемые, пригодные для упрощения.
11.
Таблица истинности1
1 1 1
2
1 1 0
3
1 0 1
4
1 0 0
5
0 1 1
6
0 1 0
7
0 0 1
8
0 0 0
Каждое выражение ложно в строке, где оно расположено, и
истинно в любой другой строке.
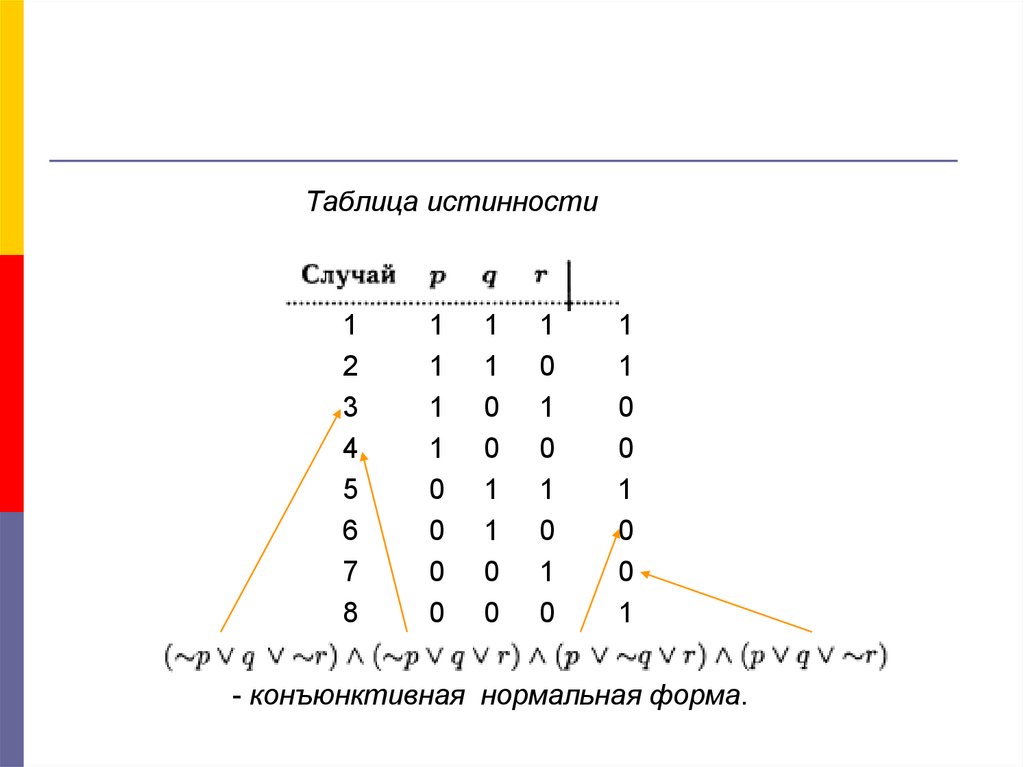
12.
Таблица истинности1
2
3
4
5
6
7
8
1
1
1
1
0
0
0
0
1
1
0
0
1
1
0
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
0
1
- конъюнктивная нормальная форма.
13. КНФ
Пусть- простые высказывания.
Выражение
,
в котором
называется элементарной дизъюнкцией.
Выражение, представляющее собой конъюнкцию элементарных
дизъюнкций, называется конъюнктивной нормальной
формой (КНФ).
Если m1 , m2 , m3, … , mn - элементарные дизъюнкции,
тогда m1 m2 m3 … mn есть конъюнктивная нормальная
форма.
14. СКНФ
Совершенная конъюнктивная нормальная форма (СКНФ) – эточастный случай КНФ, который удовлетворяет 3-м условиям:
в ней нет одинаковых множителей (элементарных дизъюнкций);
в каждом множителе нет повторяющихся переменных;
каждое множитель содержит все переменные, от которых зависит
булева функция (каждая переменная может входить в множитель
либо в прямой, либо в инверсной форме).
15. Сравнение ДНФ и КНФ
В ДНФ перечисляются все случаи (=наборы),которые надо «включить», то есть в которых
функция принимает значение 1.
В КНФ перечисляются все случаи (=наборы),
которые надо «исключить», то есть в которых
функция принимает значение 0.












 Математика
Математика








