Похожие презентации:
Алгебра высказываний
1.
Алгебра высказываний2.
Из высказываний путем соединения ихразличными способами (с помощью связок
«не», «и», «или», «следует», «равносильно»)
можно составлять новые, более сложные
высказывания.
При этом главное внимание уделяется
истинностно-функциональным комбинациям, в
которых истинность или ложность новых
высказываний определяется истинностью или
ложностью составляющих их высказываний.
3.
Определение. Отрицанием высказыванияназывается высказывание
(читается «не
»),
которое истинно в том и только том случае, если
высказывание ложно.
Таблица истинностных значений операции
отрицания
1 0
0 1
4.
Определение.Конъюнкцией
называется высказывание
высказываний
(читается «
»),
которое истинно в том и только том случае, если оба
высказывания
истинны.
Дизъюнкцией
высказывание
ложно в том
высказывания
высказываний
называется
(читается «
и только
ложны.
том
»), которое
случае,
если
оба
5.
Импликациейвысказывание
высказываний
называется
(читается «
»), которое
ложно в том и только том случае, если высказывание
истинно, а высказывание
ложно.
Эквивалентностью высказываний
высказывание
(читается «
называется
»),
которое истинно в том и только том случае, если
высказывания
и
имеют одинаковое истинностное
значение.
6.
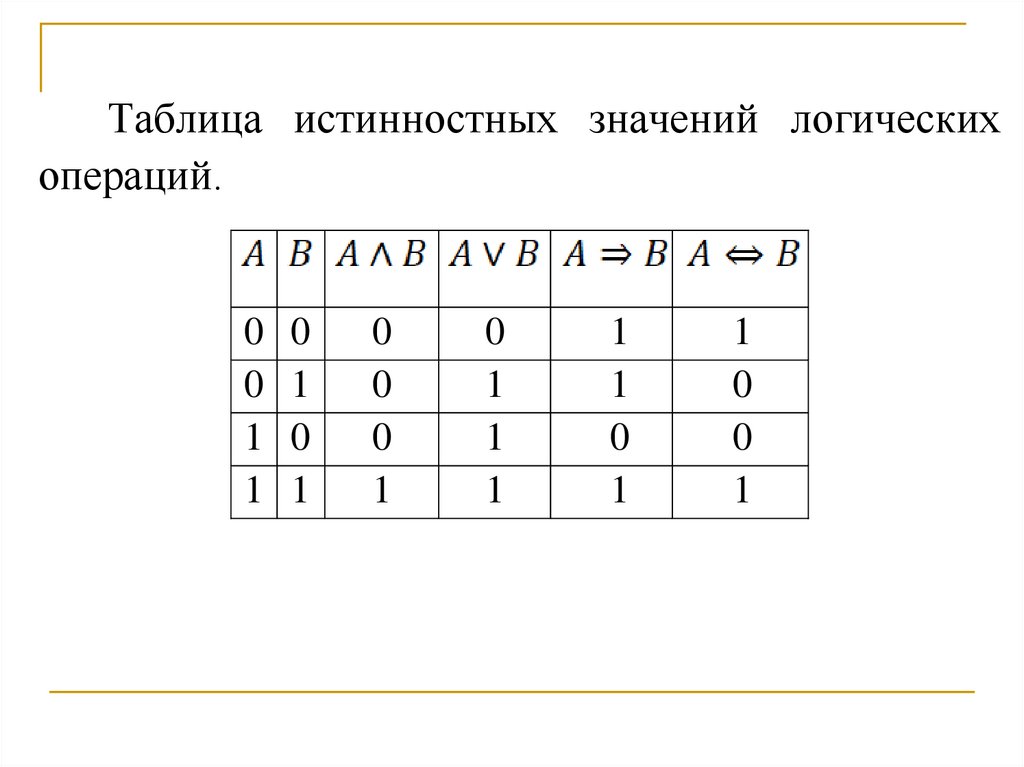
Таблица истинностных значений логическихопераций.
0
0
1
1
0
1
0
1
0
0
0
1
0
1
1
1
1
1
0
1
1
0
0
1
7.
Определение.Алгеброй
высказываний
называется множество всех высказываний P с
логическими операциями , , , , .
8.
Формулы алгебрывысказываний
9.
Свойстваалгебры
высказываний
P
описываются с помощью формул, которые
строятся из переменных символов с помощью
знаков логических операций. Такие формулы
приято называть также пропозициональными
формулами
Cимволы логических операций , , , , ,
которые называются пропозициональными
связками.
Переменные символы X,Y,Z,…, которые
используются для обозначения высказываний,
называются пропозициональными переменными.
10.
Определение.Формулы
алгебры
высказываний индуктивно определяются по
правилам:
1) каждая пропозициональная переменная
является формулой,
2) если , – формулы, то формулами
являются также выражения
( ), , , , .
Множество
всех
формул
высказываний обозначим FАВ .
алгебры
11.
Для упрощения записи формул скобки вних по возможности опускаются с учетом
следующего
приоритета
выполнения
логических операций: ¬,˄,˅ и остальные.
Так, формула
сокращенно записывается в виде
12.
Если в формулу входят переменныеX 1 ,..., X n , то записывают ( X 1 ,..., X n ) .
Из индуктивного определения формул
следует, что если в формулу вместо
переменных X1,..., X n подставить произвольные
конкретные высказывания A1 ,..., An , то получится
некоторое сложное высказывание ( A1,..., An ) .
Истинностное значение
высказывания
( ( A1 ,..., An ))
определяется истинностными
значениями
исходных
высказываний
( A1 ),..., ( An ) согласно таблицам истинностных
значений логических операций , , , , .
13.
Формула определяет функцию nF ,
переменных
которая
каждому
упорядоченному набору ( ( X 1 ),..., ( X n )) n
элементов
множества
{0,1}
ставит
в
соответствие элемент ( ( X 1 ,..., X n )) этого же
множества.
Функция F называется истинностной
функцией
формулы
и
графически
представляется истинностной таблицей.
Такая таблица содержит 2n строк и имеет
2n
2 возможных
одно
из
распределений
значений 0 и 1 в последнем столбце.
14.
Пример.Формула ( X Y X Y )
имеет следующую истинностную таблицу:
X
0
0
1
1
Y
0
1
0
1
X
1
1
0
0
Y X Y X Y X Y X Y
1
1
1
1
0
0
0
1
1
0
1
0
0
0
1
0
15.
Пример.формулы
Составим
1
5
таблицу
2
4
истинности
для
3
P Q Q P
P
0
0
1
1
Q
0
1
0
1
1
2
3
4
5
1
1
0
1
1
0
1
0
1
1
0
0
1
1
0
1
1
1
1
1
Таблица показывает, что, какого бы истинностного
значения высказывания ни подставлялись в данную
формулу вместо пропозициональных переменных P и
Q, формула всегда превращается в истинное
высказывание. Значит, формула – тавтология.
16.
Определение. Формула называется:тавтологией
(или
тождественно
истинной формулой) и обозначается | ,
если
ее
истинностная
функция
тождественно равна 1;
противоречием
(или
тождественно
ложной формулой), если ее истинностная
функция тождественно равна 0;
выполнимой, если ее истинностная функция
не равна тождественно 0;
опровержимой, если ее истинностная
функция не равна тождественно 1.
17.
Тавтологии являются общими схемамипостроения истинных высказываний и в этом
смысле выражают некоторые логические законы.
Примеры таких законов являются:
| X X – закон исключенного третьего,
| X X – закон двойного отрицания,
| ( X X ) – закон противоречия,
| ( X Y ) ( Y X ) – закон контрапозиции.
18.
Новыетавтологии
можно
получить
помощью следующего правила.
Правило подстановки:
если
1 ,..., n
| ( X 1 ,..., X n ) ,
тавтологией
( 1 ,..., n ) .
то для любых формул
является
формула
с
19.
Логическаяравносильность формул
20.
Определение. Формулы , называютсялогически
равносильными
(или
просто
равносильными), если | .
Для обозначения логически эквивалентных
формул используется символическая запись
, или просто .
Такие выражения называются логическими
равенствами или просто равенствами формул.
21.
Лемма 1. Справедливы следующие равенстваформул:
1) X (Y Z ) ( X Y ) Z , X (Y Z ) ( X Y ) Z
– свойства ассоциативности дизъюнкции и
конъюнкции;
2) X Y Y X , X Y Y X – свойства
коммутативности дизъюнкции и конъюнкции;
X X X
3) X X X ,
– свойства
идемпотентности дизъюнкции и конъюнкции;
4) X (Y Z ) ( X Y ) ( X Z ) ,
X (Y Z ) ( X Y ) ( X Z )
–
законы
дистрибутивности конъюнкции относительно
дизъюнкции
и
дизъюнкции
относительно
конъюнкции;
22.
( X Y ) X Y5) ( X Y ) X Y ,
–
законы де Моргана;
6) ( X Y ) X X , ( X Y ) X X – законы
поглощения;
7) X X – закон двойного отрицания;
X Y ( X Y )
8) X Y X Y ,
–
взаимосвязь импликации с дизъюнкцией и
конъюнкцией;
9) X Y ( X Y ) (Y X ) ,
X Y ( X Y ) ( X Y )
–
взаимосвязь
эквивалентности
с
импликацией,
дизъюнкцией и конъюнкцией.
23.
Лемма (Правило замены). Если формулы ,равносильны, то для любой формулы (X ) ,
содержащей
переменную
X,
выполняется
равенство: ( ) = ( ) .
Это правило означает, что при замене в любой
формуле ( ) некоторой ее подформулы
на равносильную ей формулу получается
формула ( ) , равносильная исходной
формуле .
Такие переходы называются равносильными
преобразованиями формул.
24.
Пример.Формула ( X Y ) Z
с помощью
равенств 5),7),8) из леммы 1 равносильно
преобразовывается следующим образом:
( X Y ) Z ( X Y ) Z
( ( X Y )) Z ( X Y ) Z .
25.
Нормальные формыформул
алгебры высказываний
26.
Отношение равносильности являетсяотношением эквивалентности на множестве
всех формул FАВ, которое разбивает это
множество
на
классы
эквивалентности
[ ] { FАВ : } , определяемые формулами
FАВ .
Из основных равенств следует, что для
FАВ можно
каждой формулы
указать
равносильные ей формулы специального вида,
содержащие только символы логических
операций , , .
27.
Определение.Литерой
называется
пропозициональная переменная X или ее
отрицание X . Для обозначения литеры
используется символ X , где {0,1} и по
1
X
X , X 0 X .
определению
Определение.
Конъюнктом
(соответственно, дизъюнктом) называется
литера или конъюнкция (соответственно,
дизъюнкция) литер.
Конъюнкт
(дизъюнкт)
называется
совершенным,
если
он
содержит
все
пропозициональные
переменные
рассматриваемой формулы.
28.
Определение. Конъюнктивной нормальнойформой (сокращенно КНФ)
называется
дизъюнкт или конъюнкция дизъюнктов.
Дизъюнктивной
нормальной
формой
(сокращенно ДНФ) называется конъюнкт или
дизъюнкция конъюнктов.
При этом КНФ (соответственно, ДНФ)
называется совершенной, если совершенны все
ее дизъюнкты (соответственно, конъюнкты).
Теорема 1. Любая формула равносильна
некоторой ДНФ и некоторой КНФ.
29.
Алгоритм приведения формулык ДНФ
(соответственно, к КНФ):
1) выражаем все входящие в формулу
импликации и эквивалентности через конъюнкцию,
дизъюнкцию и отрицание;
2) согласно законам де Моргана все отрицания,
стоящие перед скобками, вносим в эти скобки и
сокращаем все двойные отрицания;
3)
согласно
законам
дистрибутивности
преобразуем формулу так, чтобы все конъюнкции
выполнялись раньше дизъюнкций (соответственно,
чтобы все дизъюнкции выполнялись раньше
конъюнкций).
30.
Теорема2.
( X 1 ,..., X n )
Любая выполнимая формула
равносильна формуле вида
где
дизъюнкция
берется
по
всем
1,..., n {0,1}n,
упорядоченным наборам
удовлетворяющим условию F 1,..., n 1 .
Такая формула определяется однозначно (с
точностью до порядка членов конъюнкций и
дизъюнкций) и называется совершенной
дизъюнктивной
нормальной
формой
(сокращенно СДНФ) формулы .
31.
Теорема 3. Любая опровержимая формула( X 1 ,..., X n ) равносильна формуле вида
где конъюнкция берется по всем упорядоченным
1,..., n {0,1}n, удовлетворяющим
наборам
условию F 1 ,..., n 0 .
Такая формула определяется однозначно (с
точностью до порядка членов конъюнкций и
дизъюнкций)
и
называется
совершенной
конъюнктивной нормальной формой (сокращенно
СКНФ) формулы .
32.
Алгоритм нахождения СДНФ и СКНФформулы ( X 1,..., X n ) :
1. Составить истинностную таблицу
формулы и добавить два столбца
«Совершенные конъюнкты» и «Совершенные
дизъюнкты».
2. Если при значениях ( X1 ) k1,..., ( X n ) kn
значение ( ( X 1 ,..., X n )) формулы равно 1, то
в соответствующей строке таблицы в столбце
«Совершенные
конъюнкты»
записываем
X1k1 X nk n
конъюнкт
и
в
столбце
«Совершенные дизъюнкты» делаем прочерк.
При этом X i1 X i и X i0 X i .
33.
3. Если при значениях ( X 1 ) m1,..., ( X n ) mnистинностное значение ( ( X 1 ,..., X n )) формулы
равно 0, то в соответствующей строке таблицы в
столбце «Совершенные дизъюнкты» записываем
X11 m1 X n1 mn
дизъюнкт
и
в
столбце
«Совершенные конъюнкты» делаем прочерк.
X1
…
Xn
...
( X 1 ,..., X n )
… … … ...
k1 … k n ...
… … … ...
m1 … mn ...
…
1
…
0
…
…
…
…
...
Совершенные Совершенные
конъюнкты
дизъюнкты
…
…
–
X1k1 X nk n
…
…
–
X11 m1 X n1 mn
…
…
34.
4. СДНФ формулы равна дизъюнкцииполученных
совершенных
конъюнктов:
( X1k1 X nk n ) … .
5. СКНФ формулы равна конъюнкции
полученных
совершенных
дизъюнктов:
( X11 m1 X n1 mn ) … .
35.
Пример. Для формулы ( X Y X Y )получаем таблицу:
X Y
СДНФ
СКНФ
0
0
1
1
0
1
0
1
1
1
0
0
X Y
X Y
-
X Y
X Y
СДНФ данной формулы в виде дизъюнкции
совершенных конъюнктов:
СКНФ данной формулы в виде конъюнкции
совершенных дизъюнктов:
36.
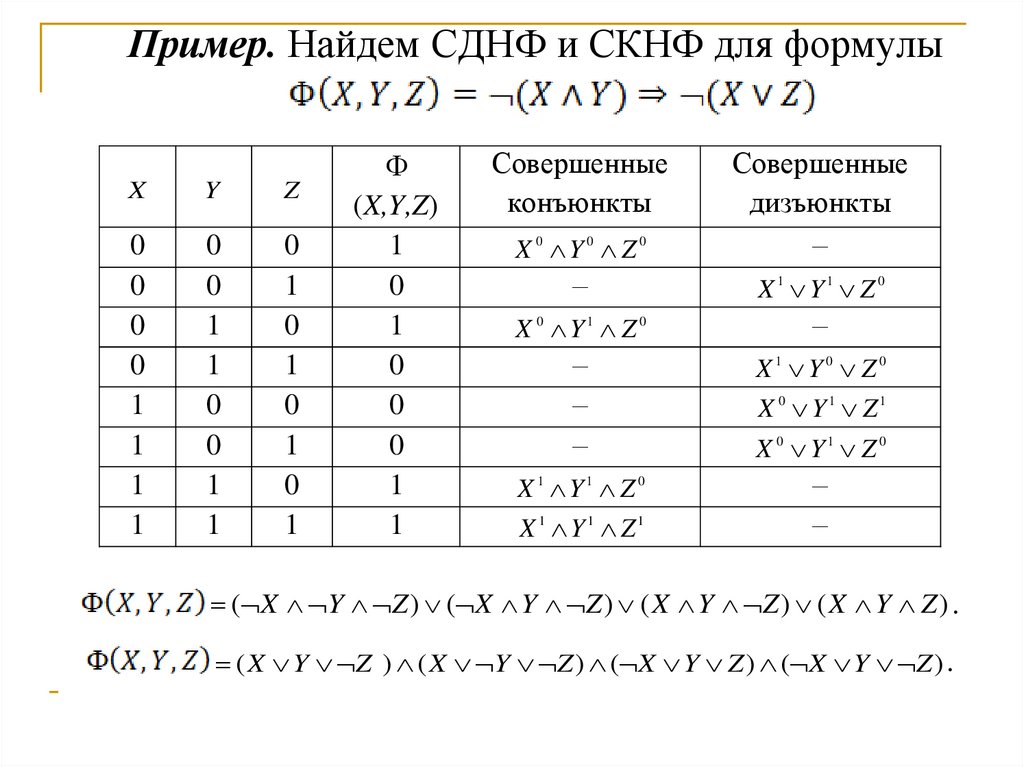
Пример. Найдем СДНФ и СКНФ для формулыX
Y
Z
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
(X,Y,Z)
1
0
1
0
0
0
1
1
Совершенные
конъюнкты
X 0 Y0 Z0
Совершенные
дизъюнкты
–
–
X 1 Y1 Z 0
X 0 Y1 Z 0
–
–
–
–
X1 Y0 Z0
X 1 Y1 Z 0
–
–
X 1 Y1 Z1
X 0 Y1 Z1
X 0 Y1 Z 0
( X Y Z ) ( X Y Z ) ( X Y Z ) ( X Y Z ) .
( X Y Z ) ( X Y Z ) ( X Y Z ) ( X Y Z ) .


































 Математика
Математика








