Похожие презентации:
Плоская система сил. Центр параллельных сил (статика, лекция 6)
1. ПЛОСКАЯ СИСТЕМА СИЛ. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.СТАТИКА
ЛЕКЦИЯ 6
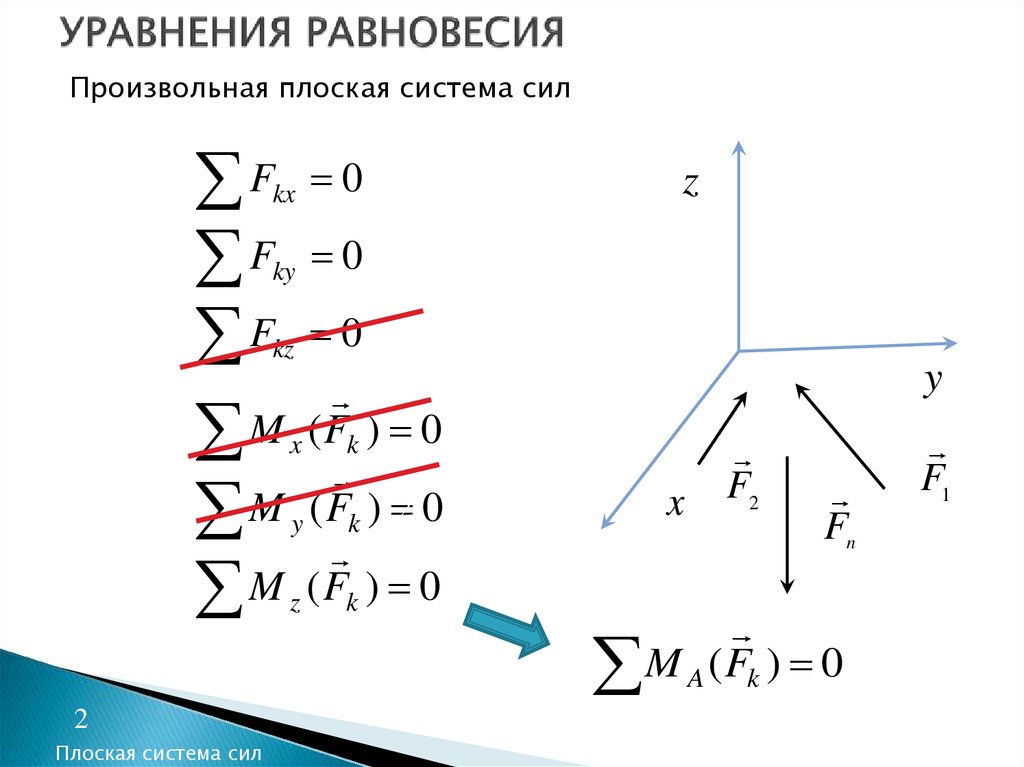
2. УРАВНЕНИЯ РАВНОВЕСИЯ
Произвольная плоская система силF
F
F
M
M
M
kx
0
ky
0
z
0
x ( Fk ) 0
2
y ( Fk ) 0
z ( Fk ) 0
kz
2
Плоская система сил
y
x
F2
Fn
M A ( Fk ) 0
F1
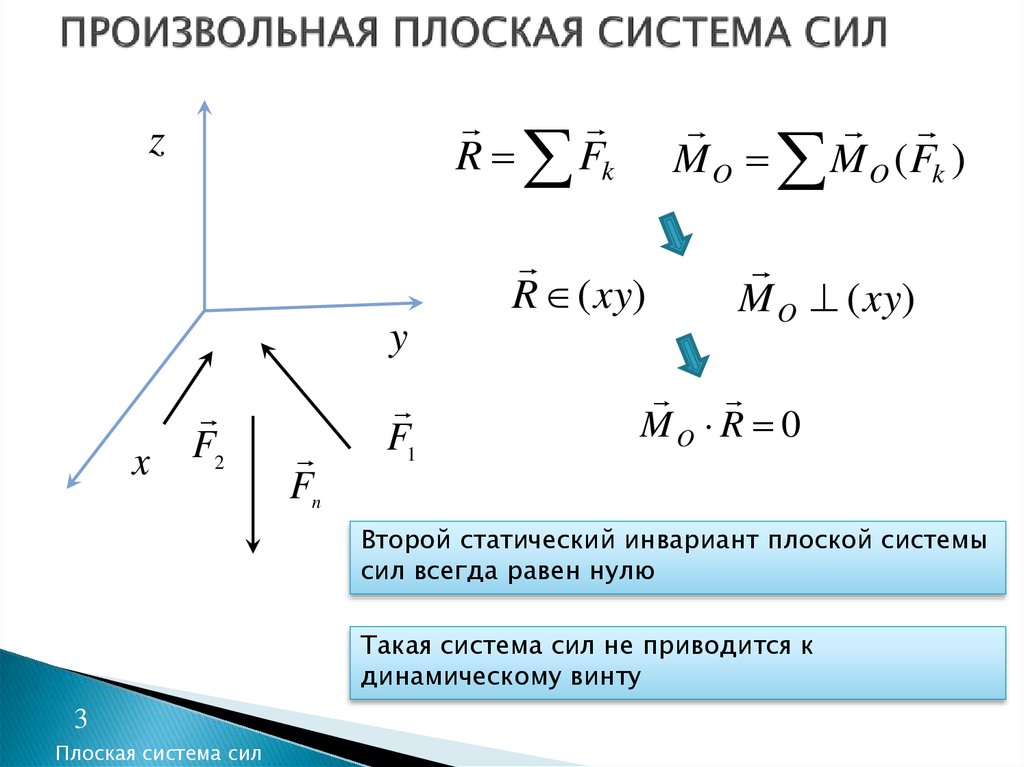
3. ПРОИЗВОЛЬНАЯ ПЛОСКАЯ СИСТЕМА СИЛ
Rz
Fk
MO
R (xy)
y
x
F2
Fn
F1
M O ( Fk )
M O (xy)
MO R 0
Второй статический инвариант плоской системы
сил всегда равен нулю
Такая система сил не приводится к
динамическому винту
3
Плоская система сил
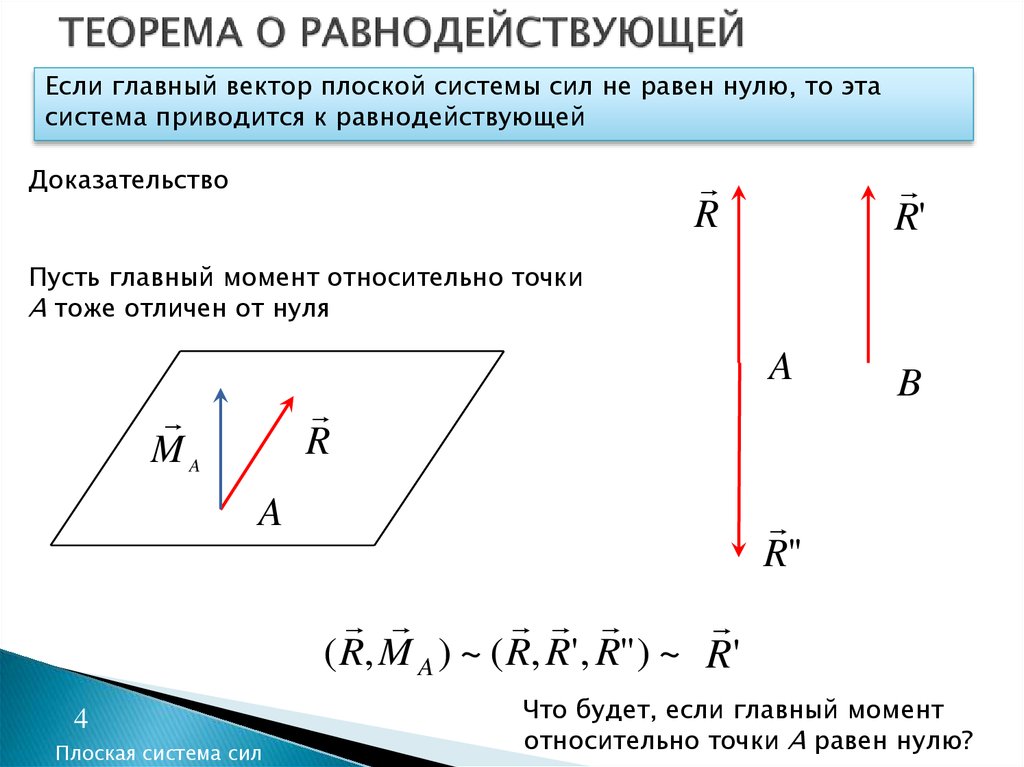
4. ТЕОРЕМА О РАВНОДЕЙСТВУЮЩЕЙ
Если главный вектор плоской системы сил не равен нулю, то этасистема приводится к равнодействующей
Доказательство
R
R'
Пусть главный момент относительно точки
А тоже отличен от нуля
A
R
MA
A
B
R''
( R, M A ) ~ ( R, R' , R") ~ R'
4
Плоская система сил
Что будет, если главный момент
относительно точки А равен нулю?
5. ФОРМЫ УРАВНЕНИЙ РАВНОВЕСИЯ ПлСС
FM
Fkx 0
1.
0
A ( Fk ) 0
ky
2.
Fkx 0
M A ( Fk ) 0
M B ( Fk ) 0
R
5
Плоская система сил
A, B, C не лежат
на одной прямой
AB x
A
3.
M A ( Fk ) 0
M B ( Fk ) 0
M C ( Fk ) 0
?
B
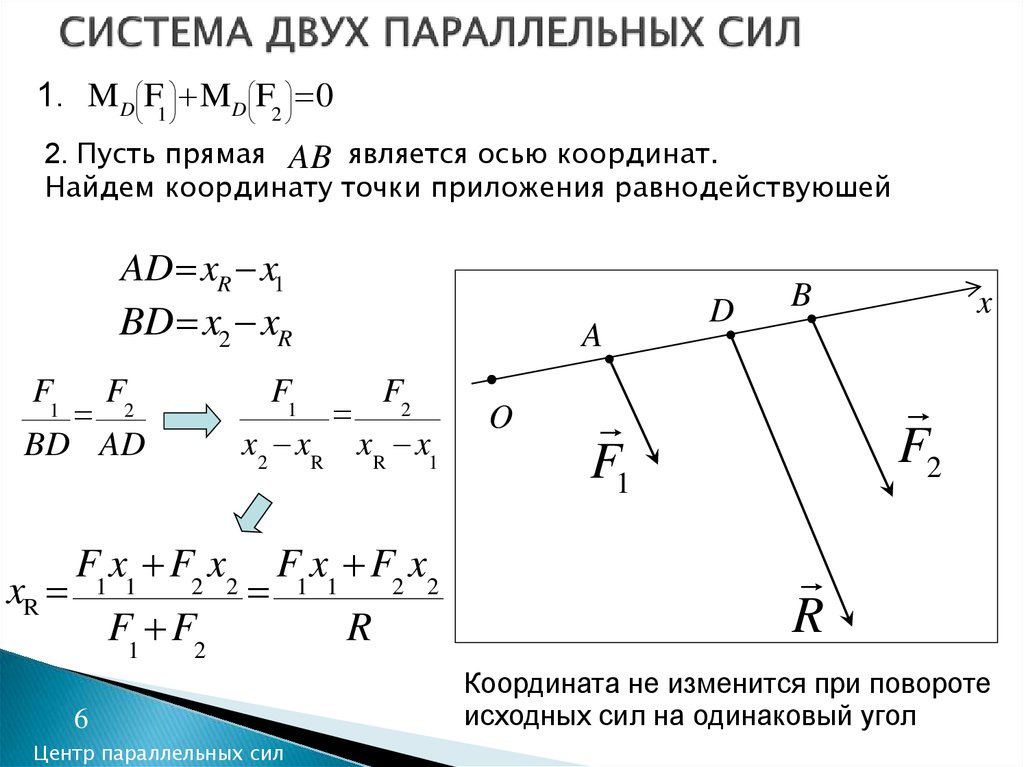
6. СИСТЕМА ДВУХ ПАРАЛЛЕЛЬНЫХ СИЛ
1. MD F1 MD F2 02. Пусть прямая AB является осью координат.
Найдем координату точки приложения равнодействуюшей
AD xR x1
BD x2 xR
F1
F2
BD AD
F1
A
F2
x2 xR xR x1
F1 x1 F2 x2 F1 x1 F2 x2
xR
F1 F2
R
6
Центр параллельных сил
O
D
B
x
F2
F1
R
Координата не изменится при повороте
исходных сил на одинаковый угол
7. СИСТЕМА ТРЕХ ПАРАЛЛЕЛЬНЫХ СИЛ
x1,2,3x
x
2
x1 1,2
O
F1
F2
R1, 2
x3
F3
R1, 2, 3
x
xR
R1,2 x1,2 F3 x3
R1,2 F3
F1 x1 F2 x2 F3 x3 F1 x1 F2 x2 F3 x3
xR
F1 F2 F3
R
7
Центр параллельных сил
8. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ
Центр параллельных сил – точка приложения равнодействующейсистемы параллельных сонаправленных сил
F1 x1 F2 x2 ... FN xN Fk xk
xC
F1 F2 ... FN
R
Изменение ориентации системы сил – изменение направления сил на
одинаковый угол при неизменных точках приложения
8
Центр параллельных сил
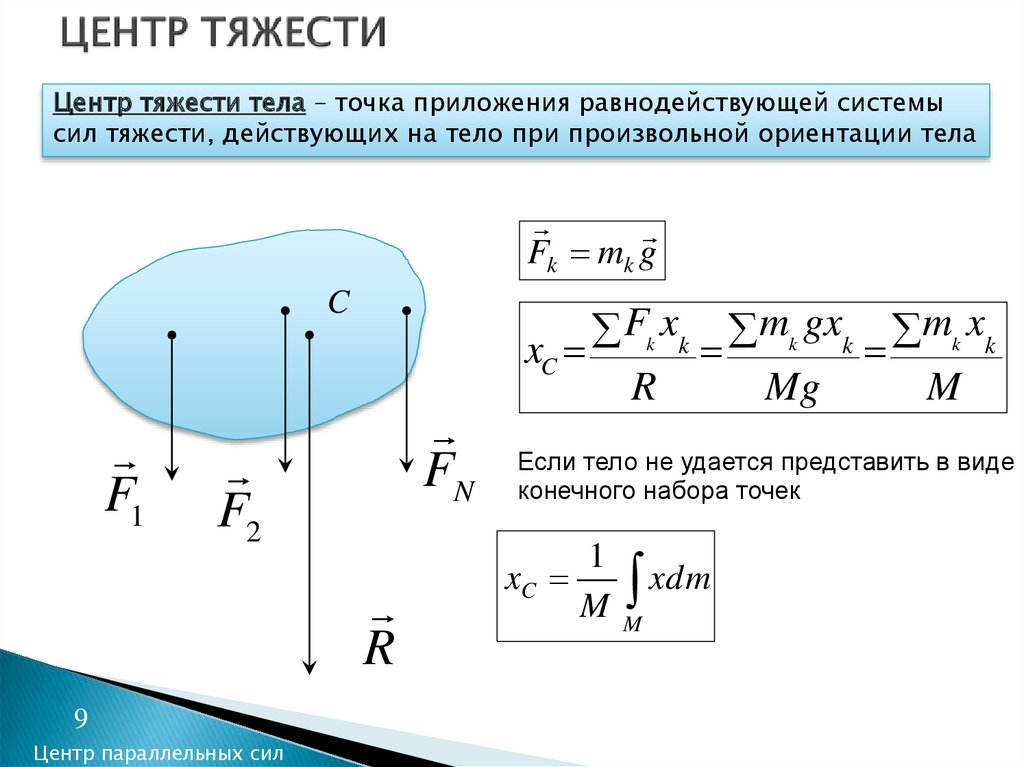
9. ЦЕНТР ТЯЖЕСТИ
Центр тяжести тела – точка приложения равнодействующей системысил тяжести, действующих на тело при произвольной ориентации тела
Fk mk g
C
F1
FN
F2
R
9
Центр параллельных сил
Fk xk mk gxk mk xk
xC
R
Mg
M
Если тело не удается представить в виде
конечного набора точек
1
xC
M
xdm
M
10. ЦЕНТР ТЯЖЕСТИ
1xC
M
1
xdm
M
M
1
x V ( x, y, z )dV
M
V
Для однородного тела
xC
V
M
V
Для однородного плоского тела
Для одномерного тела
10
Центр параллельных сил
x
V
( x, y, z )dxdydz
V
1
xdxdydz
V
1
xC
S
xdxdydz
V
xdxdy
S
1
xC
xdl
LL
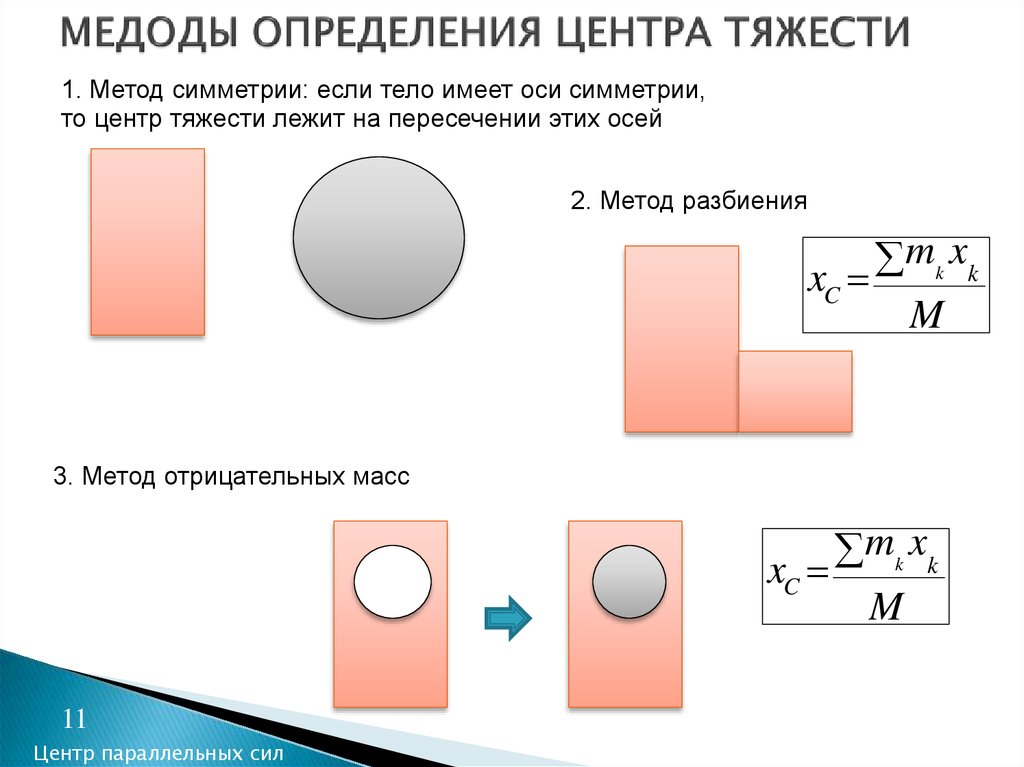
11. МЕДОДЫ ОПРЕДЕЛЕНИЯ ЦЕНТРА ТЯЖЕСТИ
1. Метод симметрии: если тело имеет оси симметрии,то центр тяжести лежит на пересечении этих осей
2. Метод разбиения
mk xk
xC
M
3. Метод отрицательных масс
mk xk
xC
M
11
Центр параллельных сил
12. МЕДОДЫ ОПРЕДЕЛЕНИЯ ЦЕНТРА ТЯЖЕСТИ
Почему центр тяжести произвольного треугольника находится в точкепересечении медиан?
12
Центр параллельных сил
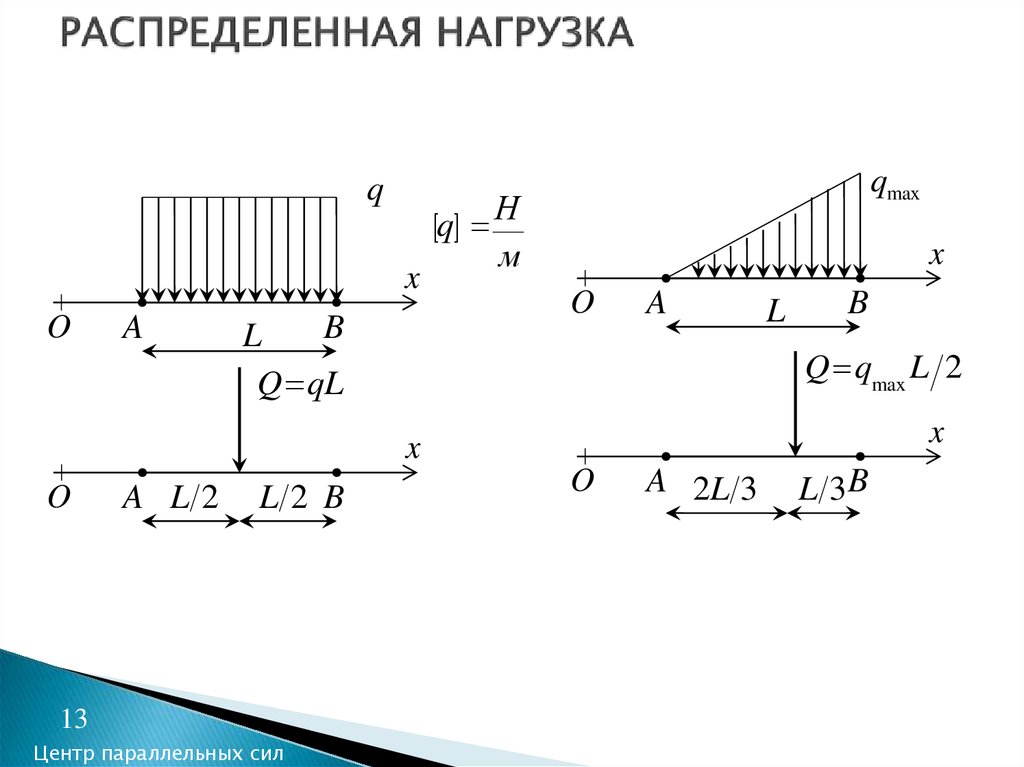
13. РАСПРЕДЕЛЕННАЯ НАГРУЗКА
qx
O
A
B
L
Q qL
qmax
q Н
м
x
O
A
L
B
Q qmax L 2
x
x
O
A L2
L2 B
13
Центр параллельных сил
O
A 2L 3
L 3B
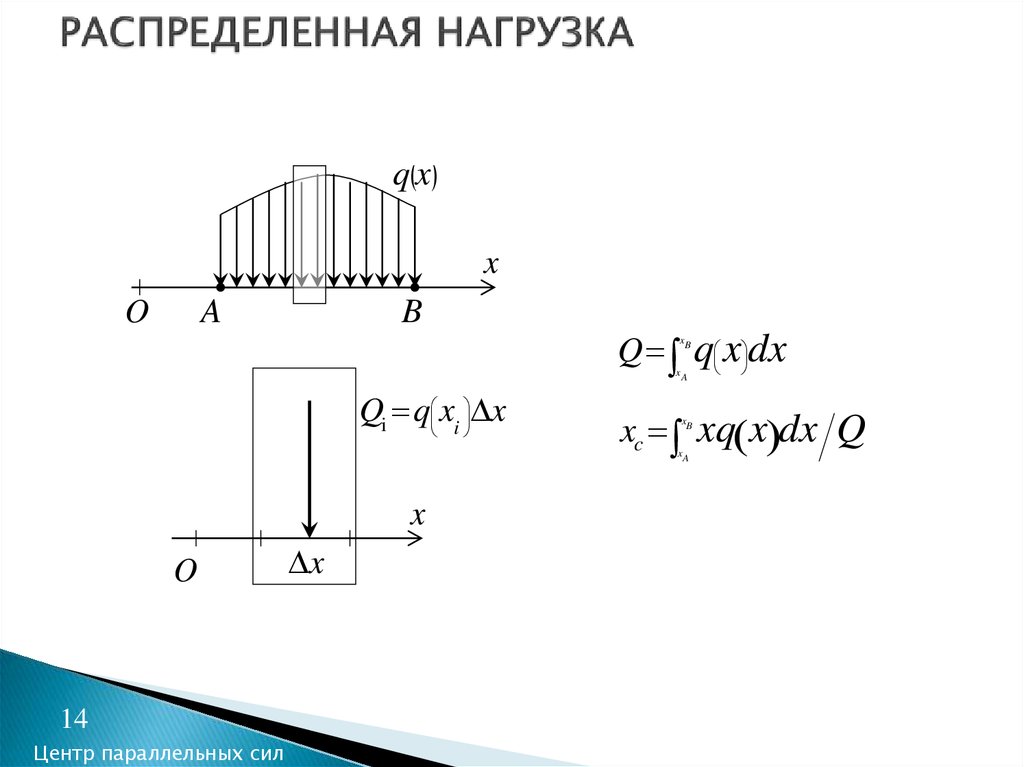
14. РАСПРЕДЕЛЕННАЯ НАГРУЗКА
q xx
O
A
B
Q q x dx
xB
xA
Qi q xi x
xc xq x dx Q
xB
xA
x
O
14
Центр параллельных сил
x






 Физика
Физика Механика
Механика