Похожие презентации:
Центр системы параллельных сил
1. ЦЕНТР СИСТЕМЫ ПАРАЛЛЕЛЬНЫХ СИЛ
. ..
Теорема Вариньона
n
M O ( R ) M O ( Fk )
M1
.
.
F1
r1
F1
M2
F2
k 1
n
F2
rC R rk Fk
C
rC
r2
R
Fn
R
.
Fn
.
rn
z
k 1
Mn
Введем единичный вектор e ,
задающий направления сил.
Fk*e , если Fk e
Тогда Fk *
.
Fk e , если Fk e
n *
R Fk F e Fk e
k 1
k 1
k 1
n
n
*
k
O
x
.
y
n
n *
n *
n *
*
rC Fk e rk Fk e rC Fk e rk Fk e
k 1
k 1
k 1
k 1
Центром системы параллельных сил называют геометрическую точку,
через которую проходит линия действия равнодействующей системы
параллельных сил при любом повороте всех этих сил вокруг точек их
приложения в одну и ту же сторону и на один и тот же угол.
n
rC
*
r
F
k k
k 1
n
F
k 1
*
k
.
1
2. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
zr1
C
P1
rC
O
x
.
Центром тяжести твердого тела
называют геометрическую точку,
неизменно связанную с телом
и являющуюся центром системы
параллельных сил тяжести,
действующих на все частицы
этого тела.
Разобъём тело на элементарные
zc
P
rn
Pn
yc
y
xc
объёмы, тогда вес тела
n
P lim k Vk
n
k 1
( x, y, z )dxdydz.
(V )
Используя формулы, определяющие центр параллельных сил тяжести,
действующих на отдельные элементарные объёмы тела, получим:
n
rC lim
rk k Vk
k 1
n
n
k 1
k
Vk
n
Для
1
r ( x, y, z )dxdydz. однородного
P (V )
rC lim
r
k 1
n
n
тела удельный
вес ( x, y, z ) const.
k 1
k
Vk
Vk
1
V
rdxdydz.
(V )
2
3. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Координаты центра тяжести однородного тела:n
xC lim
x
k 1
n
n
k
k 1
n
Vk
Vk
1
xdxdydz; yC lim k 1n
n
V (V )
n
yk Vk
k 1
Vk
1
ydxdydz; zC lim k 1n
n
V (V )
zk Vk
k 1
Vk
1
zdxdydz.
V (V )
Если однородное твердое тело можно разбить на конечное число
частей простейшей геометрической формы, для каждой из которых
положение центра тяжести известно, то координаты центра тяжести
n
x V
k
k
n
k
k
k
k
xC
площади
Здесь Vk , Sk ,Lk - соответстk 1
k 1
k 1
венно объёмы, площади и
n
n
n
xk Sk
yk S k
zk S k
длины частей, на которые
xC k 1n
; yC k 1n
; zC k 1n
, разбито данное тело,
Sk
Sk
Sk
а xk , yk ,zk – координаты
k 1
k 1
k 1
центров тяжести этих
n
n
n
xk Lk
yk Lk
zk Lk частей.
V
k
линии
xC
k 1
n
L
k 1
k
k 1
n
V
; zC
z V
объёма
k 1
n
; yC
yV
n
k
; yC
k 1
n
L
k 1
k
k 1
n
,
V
k
; zC
k 1
n
L
k 1
k
.
3
4. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Метод отрицательных весов.Это разновидность метода разбиения на части т.к. условно считается,
что полости имеют отрицательные веса.
Введем обозначения:
Р П - вес тела с полостями,
2
rП - радиус-вектор центра тяжести
3
тела, содержащего полости
k
1
Р1 , Р 2 , , Р к - вес полостей,
заполненных веществом тела,
Радиус-вектор центра тяжести r , r , , r - радиусы-векторы центров
1 2
к
тела с полостями:
тяжести полостей.
Тогда вес сплошного тела
r Р - r1 Р1 - r2 Р 2 - - rк Р к
rП
.
Р Р П Р1 Р 2 Р к , а радиус- вектор
Р - Р1 - Р 2 - - Р к
центра тяжести сплошного тела:
r Р r Р r Р rк Р к
r П П 1 1 2 2
.
Р П Р1 Р 2 Р к
4
5. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
Использование материальной симметрии.Если однородное твердое тело имеет плоскость, ось или центр
материальной симметрии, то центр тяжести этого тела лежит
соответственно или в плоскости или на оси или в центре симметрии.
z
Пусть однородное твердое тело имеет
плоскость материальной симметрии.
Совместим эту плоскость с координатной
∆Vk
zk
O
y
xk
yk
zj
x
плоскостью xOy.
∆Vj
Разобьём тело на элементарные объёмы,
так что Vk Vj , при этом x j xk , y j yk , z j zk .
1 n
Тогда z C zi Vi 0.
V i 1
Таким образом доказано, что центр тяжести тела
лежит в плоскости материальной симметрии.
Замечание.
Ось материальной симметрии тела является линией пересечения двух
плоскостей симметрии, а центр материальной симметрии – точкой
пересечения трех плоскостей симметрии. Поэтому, в силу выше
доказанного центр тяжести тела должен лежать на оси материальной
симметрии или в центре материальной симметрии тела.
5
6. ЦЕНТР ТЯЖЕСТИ ТВЕРДОГО ТЕЛА
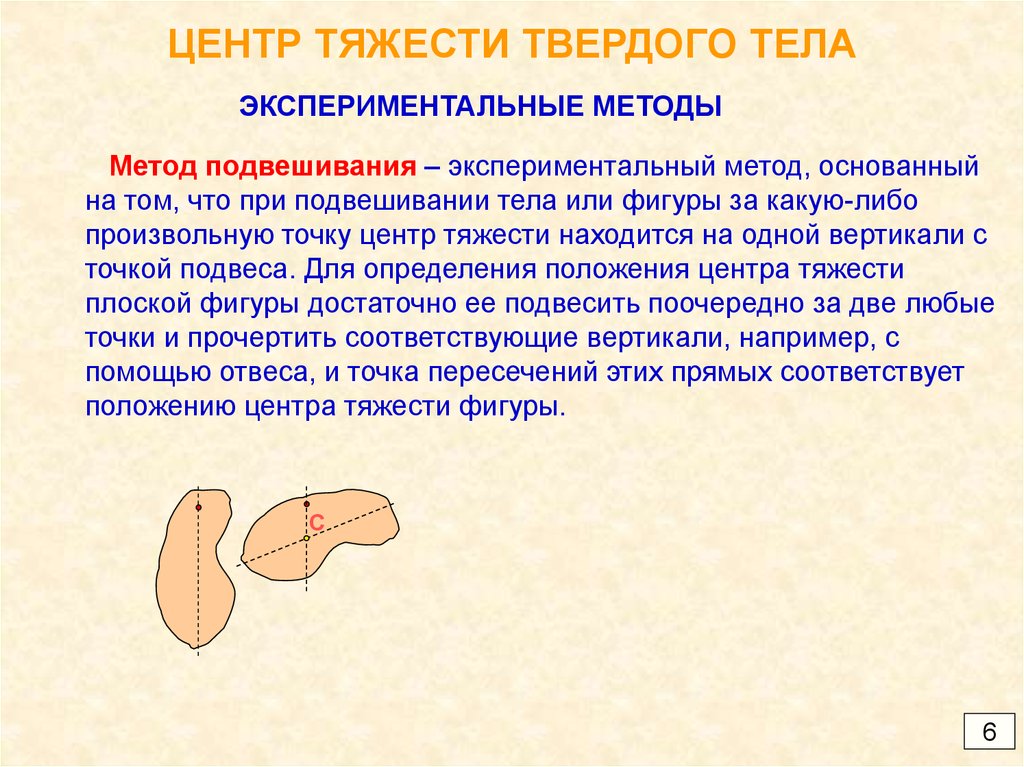
ЭКСПЕРИМЕНТАЛЬНЫЕ МЕТОДЫМетод подвешивания – экспериментальный метод, основанный
на том, что при подвешивании тела или фигуры за какую-либо
произвольную точку центр тяжести находится на одной вертикали с
точкой подвеса. Для определения положения центра тяжести
плоской фигуры достаточно ее подвесить поочередно за две любые
точки и прочертить соответствующие вертикали, например, с
помощью отвеса, и точка пересечений этих прямых соответствует
положению центра тяжести фигуры.
С
6
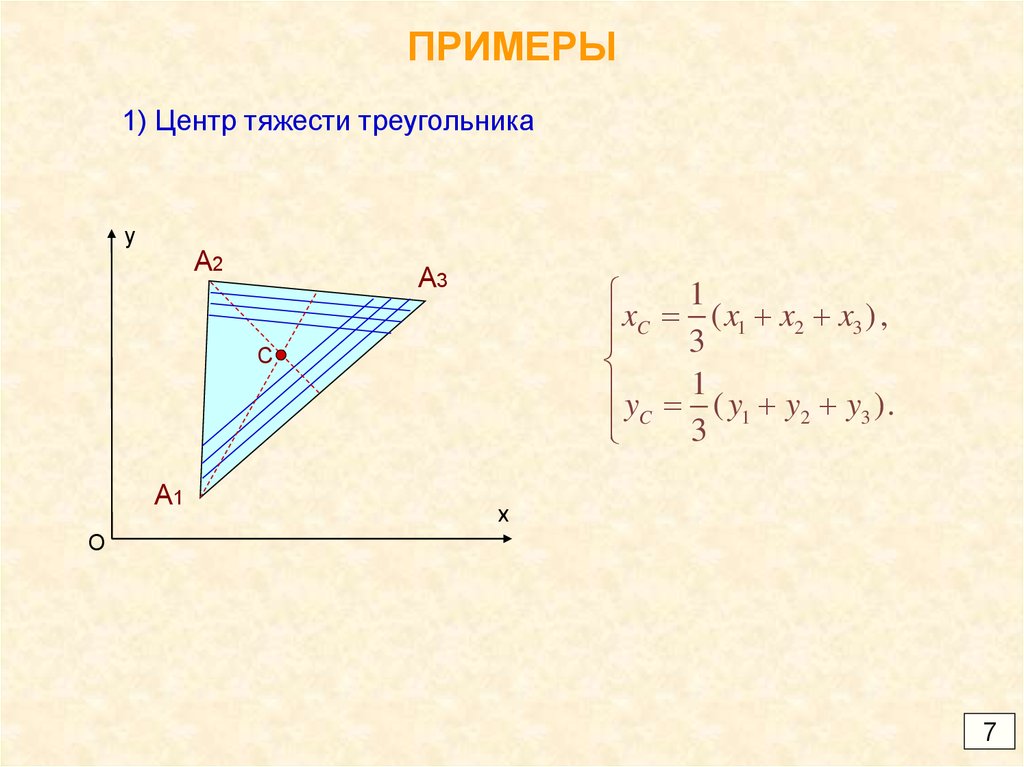
7. ПРИМЕРЫ
1) Центр тяжести треугольникаy
A2
A3
1
xC 3 ( x1 x2 x3 ) ,
y 1 ( y y y ).
3
C 3 1 2
C
A1
x
O
7
8. ПРИМЕРЫ
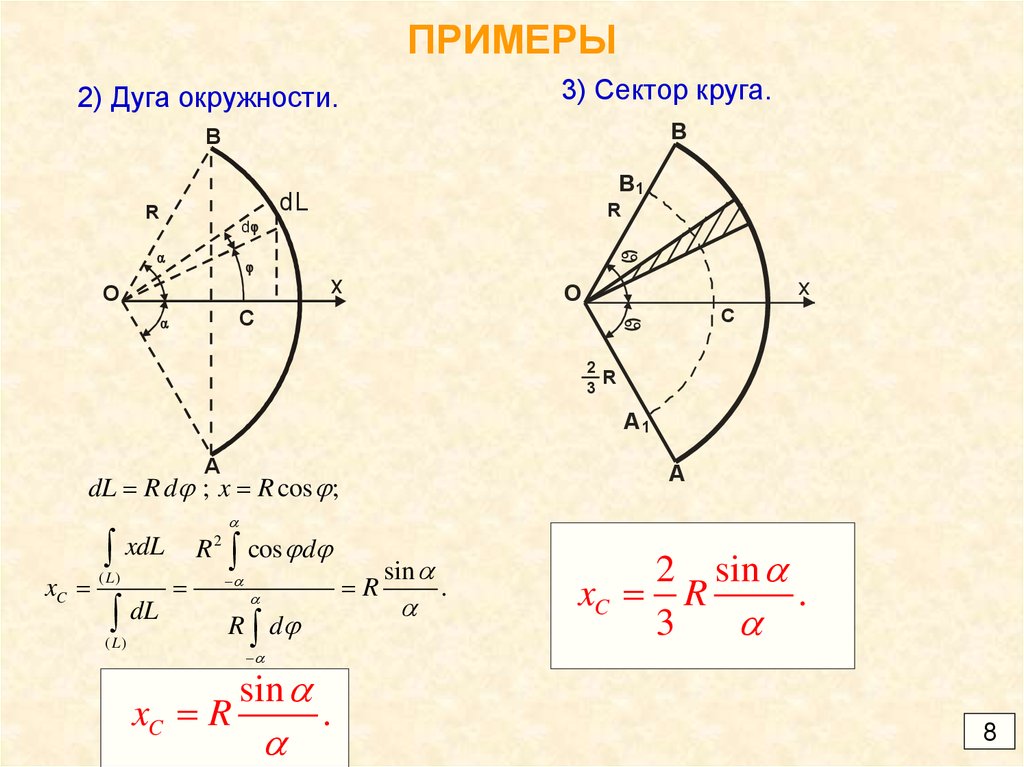
3) Сектор круга.2) Дуга окружности.
B
B
R
dL
d
B1
R
a
x
O
С
x
O
C
a
2
R
3
A1
A
A
dL R d ; x R cos ;
xC
xdL
( L)
( L)
dL
R
2
cos d
R d
R
sin
.
2 sin
xC R
.
3
xC R
sin
.
8
9. ПРИМЕРЫ
4) Круговой конусZ
1 2
1
zC zdV ; V R H
V (V )
3
dz
H
r
ПРИМЕРЫ
dV r dz;
z
C
2
Y
O
R
zdV
H
0
X
(V )
H z
r
R
H
H z
z
R dz
H
2
H
R H 2
R 2z
z
z
2
2H
2 ( H 2 Hz z )zdz 2 H
H
2
3 4 0
H 0
R2 H 2
3
H
R2 H 4
R2H 2
H
zC
2
; zC
2
4
12
R H 4
H 12
12
2
2
2
3
4
9
10. ПРИМЕРЫ
5) Полушар1
2 3
zC zdV ; V R
V (V )
3
dV r dz;
2
r R2 z 2
R
z ( R z )dz
zdV
0
2
2
(V )
R
R z
z
R
( R z z )dz
0
4 0
4
2
4
R
3
r
zC
3
R
3
4 2 R 8
zC
R
2 2
2
4
4
3
8
10
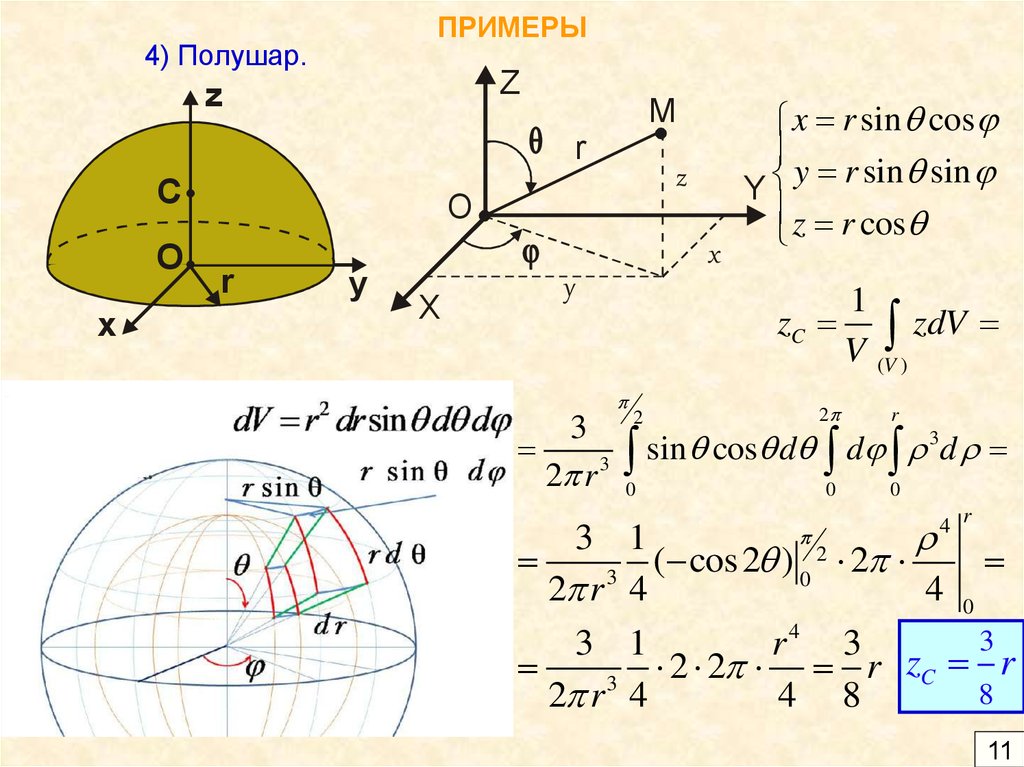
11. ПРИМЕРЫ
4) Полушар.Z
z
M
r
C
O
x
O
r
y
X
z
x
y
x r sin cos
y r sin sin
Y
z r cos
1
zC zdV
V (V )
3
2 r 3
3
2 r 3
3
2 r 3
2
2
r
0
0
3
sin
cos
d
d
d
0
4 r
1
2
( cos 2 ) 0 2
4
4 0
3
1
r4 3
2 2 r zC r
8
4
4 8
11
12. ОСНОВЫ ТЕОРИИ ТРЕНИЯ
Трение - механическое взаимодействие между поверхностями твердыхтел, возникающее в местах их соприкосновения и препятствующее
относительному перемещению тел в направлении, лежащем в плоскости
их соприкосновения.
Трение между взаимно неподвижными поверхностями называется
трением покоя.
Трение между движущимися поверхностями называется
кинематическим.
M
В зависимости от вида движения
одного тела по поверхности другого
тела различают кинематические
трение скольжения,
трение качения и
трение верчения.
При отсутствии смазки между трущимися
поверхностями трение называют сухим.
При наличии смазки между трущимися
поверхностями трение называют вязким или
жидкостным.
СB
В
FТР
M СK
V
К
12
13. ОСНОВЫ ТЕОРИИ ТРЕНИЯ
Сила трения скольжения подчиняется законам трения,установленным экспериментально Кулоном и Амонтоном:
0 FTP F
MAX
FTP f N .
MAX
TP
R
φ
N
,
F
FTP
Здесь f - безразмерный коэффициент трения
скольжения, определяемый экспериментально
и зависящий от многих факторов: материала
соприкасающихся тел, степени чистоты
R MAX
обработки их поверхности, влажности и
температуры окружающей среды и др.
Коэффициент трения скольжения не зависит
от силы нормального давления и площади
контакта трущихся поверхностей.
Углом трения называют угол φ 0 между
направлениями нормальной реакции N
и полной реакции R MAX , соответствующей
максимальному значению силы трения
MAX
MAX
скольжения F TP
.
F TP
При этом имеет место соотношение tg φ0 =
=f.
N
P
φ0
N
F
MAX
FTP
P
13
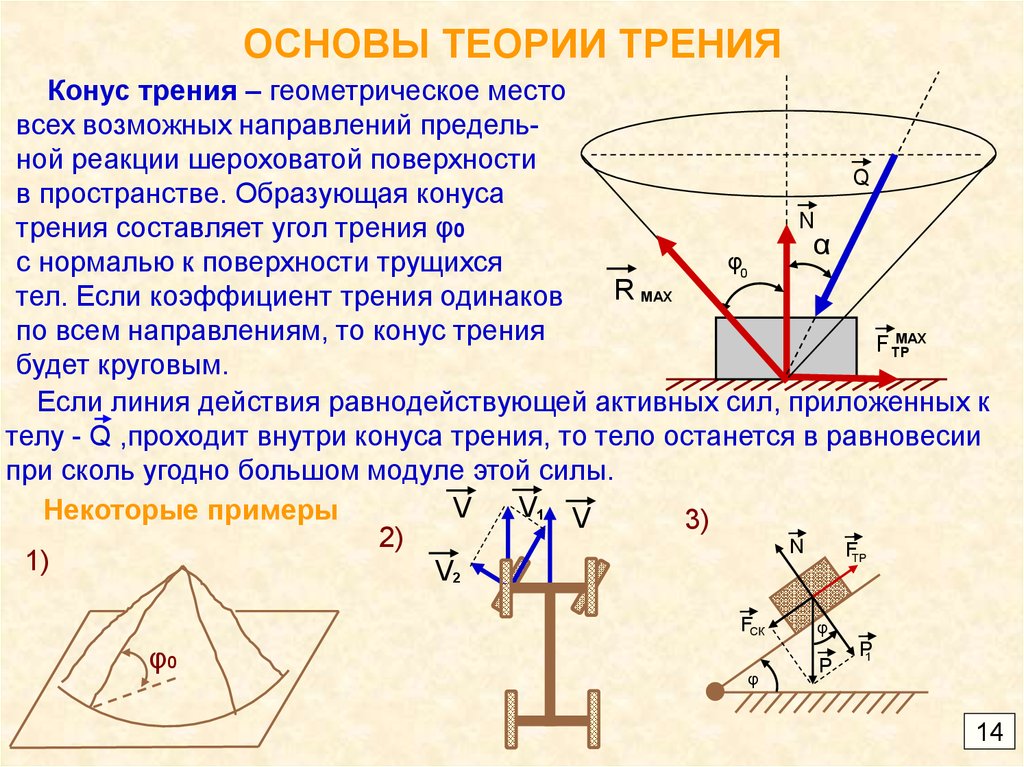
14. ОСНОВЫ ТЕОРИИ ТРЕНИЯ
Конус трения – геометрическое местовсех возможных направлений предельной реакции шероховатой поверхности
Q
в пространстве. Образующая конуса
N
трения составляет угол трения φ0
α
φ0
с нормалью к поверхности трущихся
R MAX
тел. Если коэффициент трения одинаков
по всем направлениям, то конус трения
MAX
F TP
будет круговым.
Если линия действия равнодействующей активных сил, приложенных к
телу - Q ,проходит внутри конуса трения, то тело останется в равновесии
при сколь угодно большом модуле этой силы.
V1 V
V
Некоторые примеры
3)
2)
N
FTP
1)
V2
FСК
φ0
φ
φ
P
P1
14
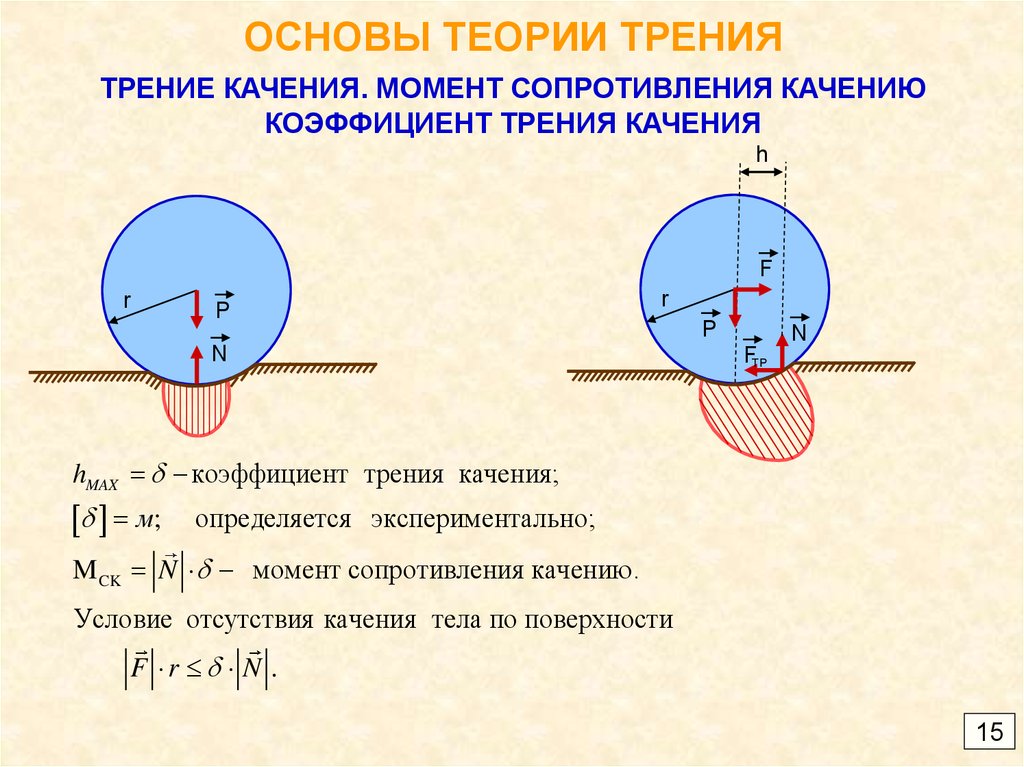
15. ОСНОВЫ ТЕОРИИ ТРЕНИЯ
ТРЕНИЕ КАЧЕНИЯ. МОМЕНТ СОПРОТИВЛЕНИЯ КАЧЕНИЮКОЭФФИЦИЕНТ ТРЕНИЯ КАЧЕНИЯ
h
F
r
P
r
N
P
N
FTP
hMAX коэффициент трения качения;
м;
определяется экспериментально;
M CK N момент сопротивления качению.
Условие отсутствия качения тела по поверхности
F r N .
15
16. ОСНОВЫ ТЕОРИИ ТРЕНИЯ
При равновесии катка выполняются условия:y
F
F
M
F
r
P
N
FTP
O
A
Пусть
r
x
F FTP 0 (1) ,
KY
N P 0 (2) ,
( FK ) F r M CK 0 (3).
При отсутствии скольжения F FTP f N f P F f P ;
A
при отсутствии качения F r M CK N P F
M CK
f , тогда: а) при 0 F
KX
r
r
P.
P каток останется в равновесии;
P F f P каток катится без проскальзывания;
r
в) при f P F каток катится со скольжением.
Пусть f , тогда: а) при 0 F f P каток останется в равновесии;
r
б) при f P F P каток скользит без вращения (поступательное движение);
r
в) при f P F каток катится со скольжением.
r
б) при
На практике
f поэтому, при возрастании силы F, каток начнет качение без скольжения, а затем будет
r
происходить качение со скольжением. По затратам энергии качение значительно выгоднее скольжения . 16
17. ОСНОВЫ ТЕОРИИ ТРЕНИЯ
M СBТРЕНИЕ ВЕРЧЕНИЯ
N
В
M CB N , м ; (10 1 0,5 10 1 ) .
Коэффициенты трения некоторых тел.
(м)
№
Материал тел,
находящихся в
соприкосновении
1
Дерево-дерево
0,4 0,7
5 10-4 8 10-4
2
Металл-металл
0,15 0,25
3
Сталь мягкая
0,16
5 10-5
4
Сталь закаленная
0,18
5 10-6 10-5
5
Сталь-кожа
0,56
6
Сталь-лед
0,02 0,03
7
Резина (шины) асфальт
0,4 0,6
2,4 10-3
f
17











 Физика
Физика








