Электромагнитная индукция. Явление электромагнитной индукции. Правило Ленца

1.

ЭЛЕКТРОМАГНИТНАЯ
ИНДУКЦИЯ
o
o
o
o
o
o
Явление электромагнитной индукции.
Правило Ленца.
Закон электромагнитной индукции.
Индукция тока в движущихся и
неподвижных проводниках.
Вихревое электрическое поле. Токи
Фуко.
Индуктивность, явление
электромагнитной самоиндукции.

2.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
• Опыты Эрстеда и Ампера показали, что электрический
ток создаёт магнитное поле.
• М. Фарадей: Возможно ли возбуждение электрического
тока посредством магнитного поля?
• 1831 г. Фарадеем открыто явление электромагнитной
индукции:
при изменении магнитного потока,
пронизывающего замкнутый проводящий контур, в
нем возникает электрический ток, который
называют индукционным.
Индукционный ток Ii возникает в результате действия на
заряды в проводнике сторонних сил, электродвижущая
сила которых называется ЭДС индукции i.

3.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
N
Ii
S
В
G
Опыт Фарадея:
При внесении магнита в катушку наблюдается отброс
стрелки гальванометра.
При движении магнита из катушки - отброс стрелки
гальванометра происходит в противоположную
сторону.
Отброс стрелки тем больше, чем быстрее движется
магнит.

4.

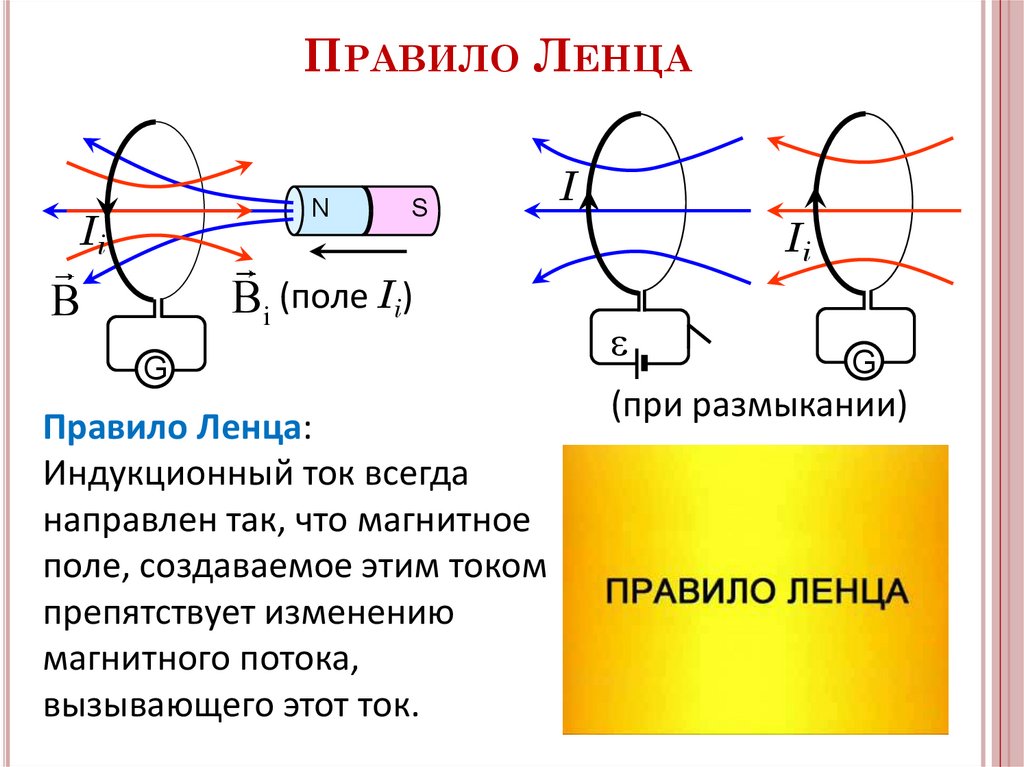
ПРАВИЛО ЛЕНЦА
N
Ii
S
Вi (поле Ii)
В
G
Правило Ленца:
Индукционный ток всегда
направлен так, что магнитное
поле, создаваемое этим током
препятствует изменению
магнитного потока,
вызывающего этот ток.
I
Ii
G
(при размыкании)

5.

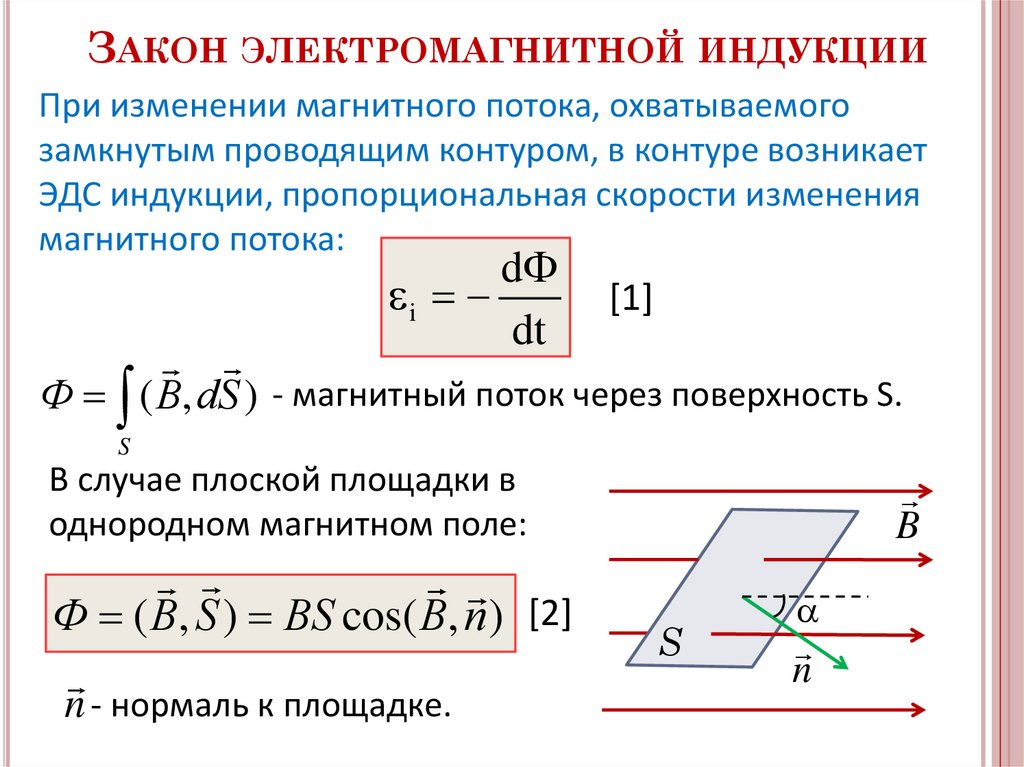
ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
При изменении магнитного потока, охватываемого
замкнутым проводящим контуром, в контуре возникает
ЭДС индукции, пропорциональная скорости изменения
магнитного потока:
dФ
i
dt
[1]
Ф ( B, dS ) - магнитный поток через поверхность S.
S
В случае плоской площадки в
однородном магнитном поле:
Ф ( B, S ) BS cos( B, n ) [2]
n - нормаль к площадке.
B
S
a
n

6.

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ
Если замкнутый контур, в котором
индуцируется ЭДС, состоит из N витков
N
k
k 1
d
εi
dt
- полный магнитный поток, охватываемый
всеми витками; Фk - магнитный поток,
охватываемый k-ым витком.
Индукционный ток в проводящем контуре можно вызвать
двумя различными способами:
1) при перемещении замкнутого проводящего контура в
стационарном магнитном поле;
2) при изменении магнитного поля, в котором находится
неподвижный контур.
Величина i не зависит от способа изменения магнитного
потока Ф.

7.

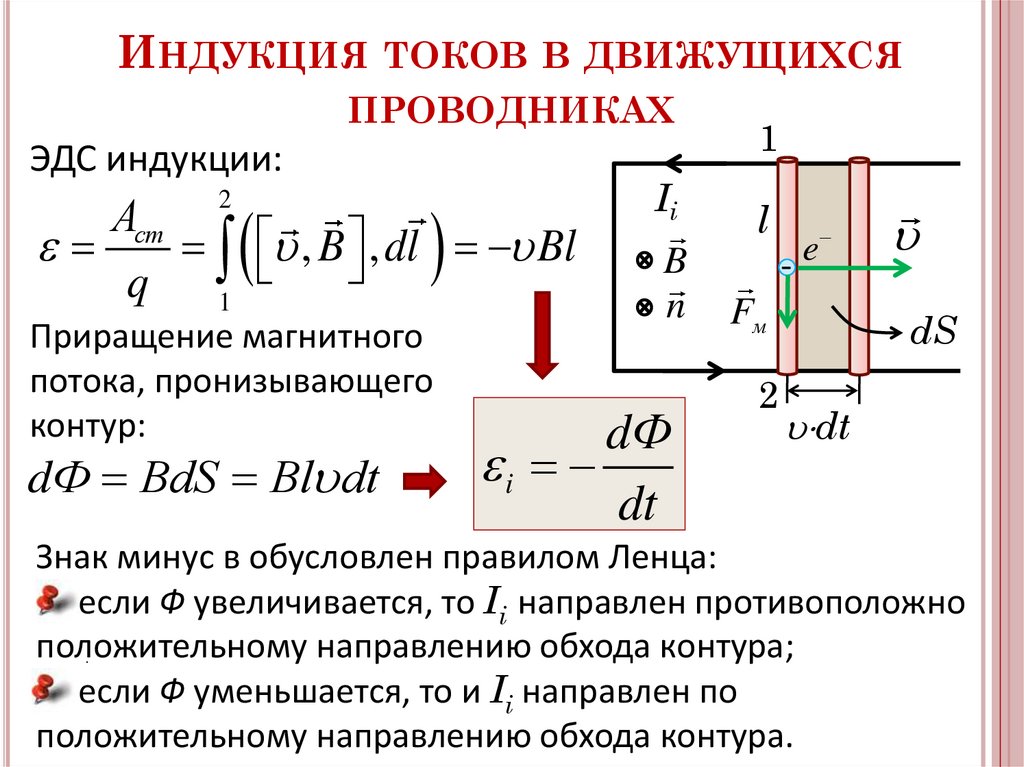
ИНДУКЦИЯ ТОКОВ В ДВИЖУЩИХСЯ
ПРОВОДНИКАХ
Пусть перемычка движется в однородном стационарном
магнитном поле с постоянной скоростью .
1
На свободные электроны в
Ii
перемычке действует сила:
l
e
B
-
F м q , B
Возникает индукционный ток Ii в
направлении противоположном
положительному направлению обхода
контура. Работа, совершаемая Fм в
перемычке длиной l:
2
2
1
1
n Fм
dS
2 dt
Аст ( Fм , dl ) q , B , dl

8.

ИНДУКЦИЯ ТОКОВ В ДВИЖУЩИХСЯ
ПРОВОДНИКАХ
ЭДС индукции:
Аст
, B , dl Bl
q
1
2
Приращение магнитного
потока, пронизывающего
контур:
dФ BdS Bl dt
1
Ii
l
B
n
Fм
dФ
i
dt
2
e
-
dS
dt
Знак минус в обусловлен правилом Ленца:
если Ф увеличивается, то Ii направлен противоположно
положительному
направлению обхода контура;
.
.
если Ф уменьшается, то и Ii направлен по
положительному направлению обхода контура.

9.

ИНДУКЦИЯ ТОКОВ В ДВИЖУЩИХСЯ
ПРОВОДНИКАХ
В рассмотренном примере работа магнитной силы F
отлична от нуля, что противоречит утверждению о том, что
сила Лоренца совершать работу не может.
Противоречие устраняется, если учесть, что при движении
электронов вдоль перемычки, со стороны магнитного
поля на них начинает действовать ещё одна магнитная
сила F , направленная перпендикулярно перемычке, в
сторону, противоположную . Она совершает
отрицательную работу, причём
AF AF
Таким образом, работа полной магнитной силы равна
нулю.

10.

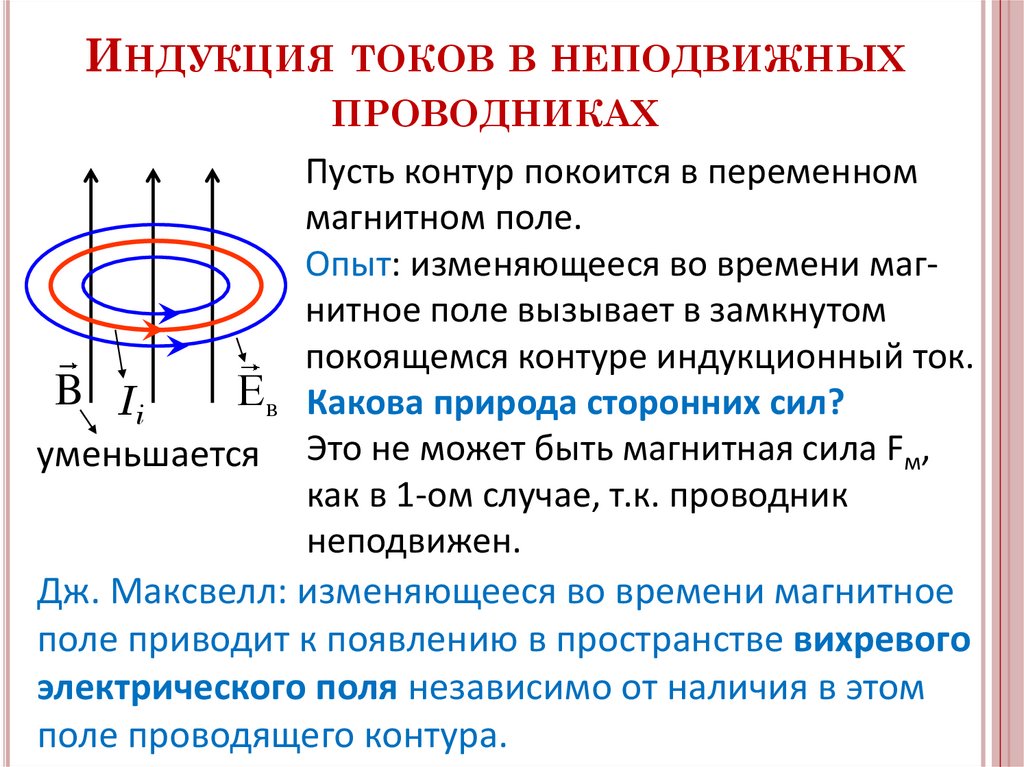
ИНДУКЦИЯ ТОКОВ В НЕПОДВИЖНЫХ
ПРОВОДНИКАХ
Пусть контур покоится в переменном
магнитном поле.
Опыт: изменяющееся во времени магнитное поле вызывает в замкнутом
покоящемся контуре индукционный ток.
B Ii
Е в Какова природа сторонних сил?
уменьшается Это не может быть магнитная сила Fм,
как в 1-ом случае, т.к. проводник
неподвижен.
Дж. Максвелл: изменяющееся во времени магнитное
поле приводит к появлению в пространстве вихревого
электрического поля независимо от наличия в этом
поле проводящего контура.

11.

ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ
В отличие от электростатического поля, создаваемого
зарядами, вихревое электрическое поле:
имеет замкнутые линии напряжённости;
не является потенциальным.
Работа сил вихревого электрического поля при перемещении заряда по замкнутому контуру не равна нулю:
Aст
i
( Eв , dl )
q
L
Закон электромагнитной
индукции примет вид:
[3]
(
E
,
dl
)
(
B
,
dS
)
L
t
S
Физический смысл: переменное магнитное поле
порождает вихревое электрическое поле.

12.

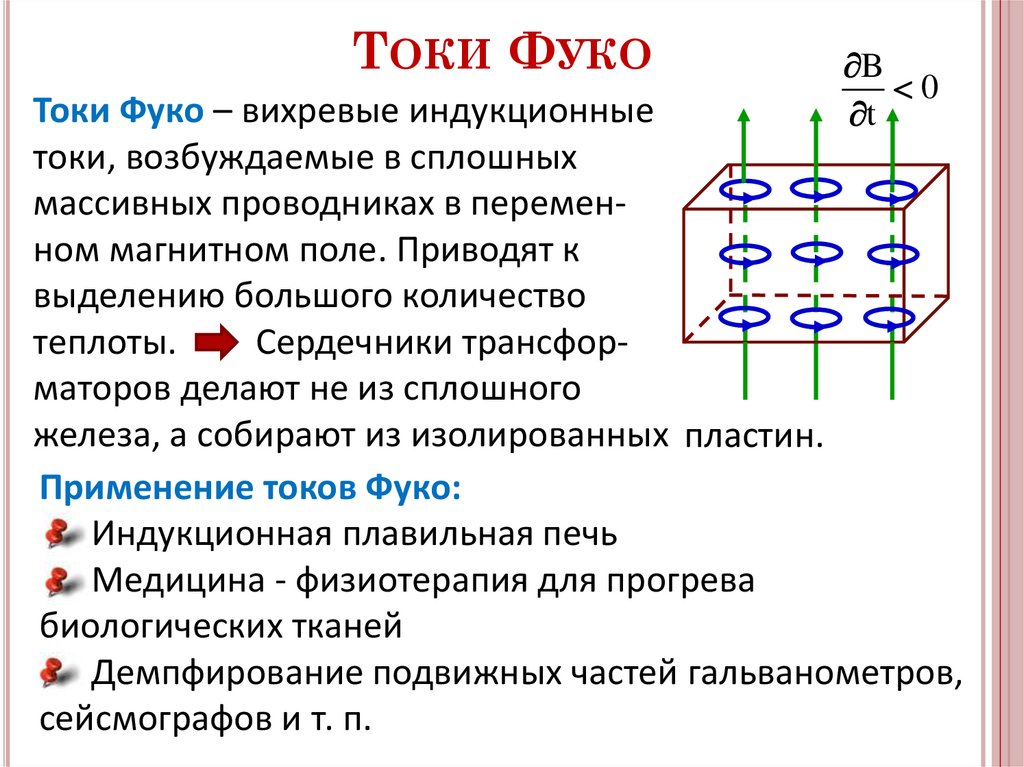
ТОКИ ФУКО
B
0
t
Токи Фуко – вихревые индукционные
токи, возбуждаемые в сплошных
массивных проводниках в переменном магнитном поле. Приводят к
выделению большого количество
теплоты.
Сердечники трансформаторов делают не из сплошного
железа, а собирают из изолированных пластин.
Применение токов Фуко:
Индукционная плавильная печь
Медицина - физиотерапия для прогрева
биологических тканей
Демпфирование подвижных частей гальванометров,
сейсмографов и т. п.

13.

ТОКИ ФУКО

14.

СКИН-ЭФФЕКТ
Если по проводнику с постоянным поперечным
сечением протекает постоянный ток, то плотность
тока одинакова во всех точках проводника.
При протекании переменного тока плотность тока
оказывается не одинаковой по сечению: она
наибольшая на поверхности и наименьшая по оси
проводника. При очень больших частотах ток
существует только в тонком поверхностном слое. Это
явление называется скин – эффектом.
Объясняется возникновением
вихревого электрического поля

15.

ИНДУКТИВНОСТЬ
Ток, текущий в контуре, создаёт пронизывающий этот
контур полный магнитный поток . При одинаковом
магнитном потоке в каждом витке:
NФ
I
N – число витков в контуре;
Ф – магнитный поток через каждый виток.
В
Согласно определению:
В
Закон Био-Савара-Лапласа: В I
LI
[6]
B
[L] = Гн = Вб/А
L – индуктивность контура, которая зависит от формы,
размеров контура и магнитных свойств среды .
В присутствии ферромагнетиков L зависит и от I,
т.к. является сложной функцией I.

16.

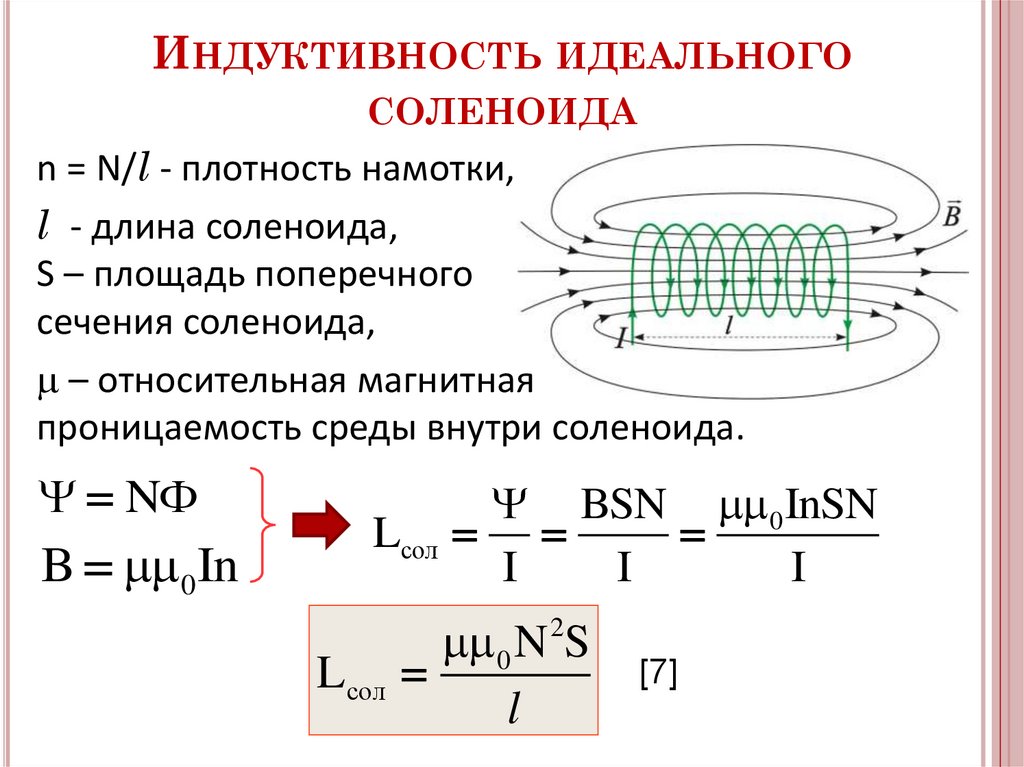
ИНДУКТИВНОСТЬ ИДЕАЛЬНОГО
СОЛЕНОИДА
n = N/l - плотность намотки,
l - длина соленоида,
S – площадь поперечного
сечения соленоида,
– относительная магнитная
проницаемость среды внутри соленоида.
NФ
B 0 In
BSN 0 InSN
Lсол
I
I
I
0 N S
Lсол
l
2
[7]

17.

ЯВЛЕНИЕ САМОИНДУКЦИИ
Изменение тока в контуре вызывает и изменение
магнитного потока, пронизывающего контур,
вследствие чего в контуре индуцируется ЭДС
самоиндукции:
d
d
dI
s
(LI) L , если L const
dt
dt
dt
dI
s L
dt
[8]
По правилу Ленца: s создаёт ток самоиндукции Is такого направления, чтобы препятствовать изменению
I. Если I увеличивается, то Is направлен противоположно I, и если I уменьшается, то Is сонаправлен с I.

18.

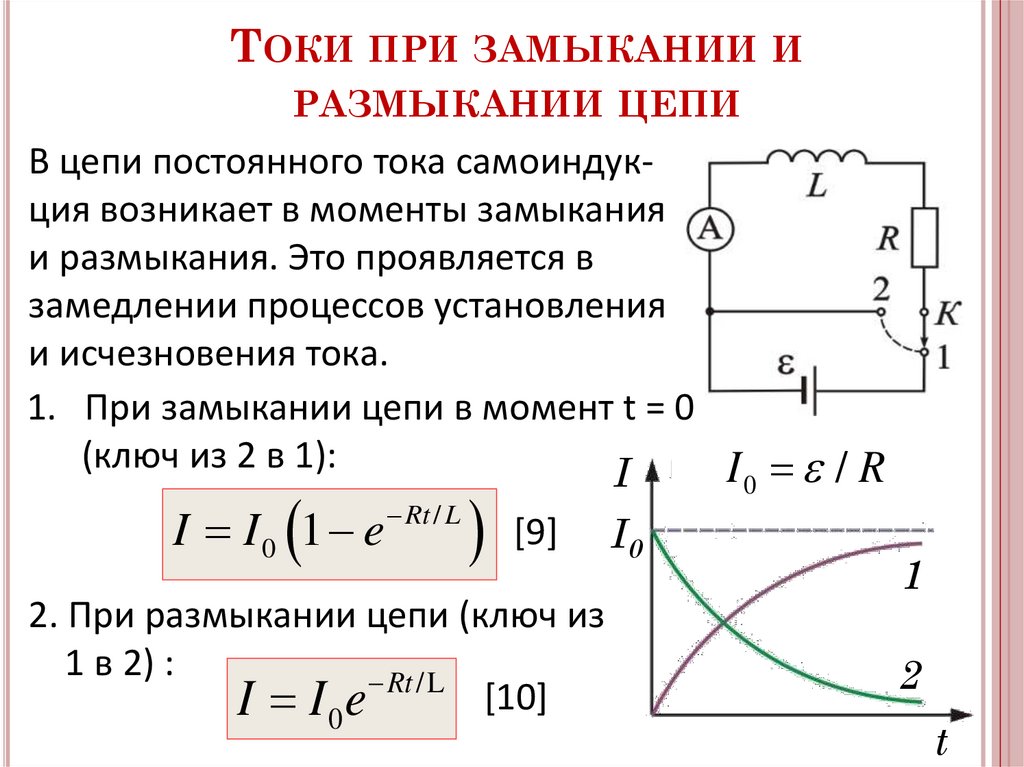
ТОКИ ПРИ ЗАМЫКАНИИ И
РАЗМЫКАНИИ ЦЕПИ
В цепи постоянного тока самоиндукция возникает в моменты замыкания
и размыкания. Это проявляется в
замедлении процессов установления
и исчезновения тока.
1. При замыкании цепи в момент t = 0
(ключ из 2 в 1):
I0 / R
I
I I 0 1 e Rt / L [9]
2. При размыкании цепи (ключ из
1 в 2) :
Rt /L
[10]
I I0e
I0
1
2
t

19.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Найдём работу, совершаемую в
цепи, при уменьшении тока от I до
0 после размыкании ключа K:
0
LI
A s Idt LIdI
2
I
2
По закону сохранения энергии эта
работа идёт на нагрев проводов и сопротивления R. В
начальный момент эта энергия была локализована в
магнитном поле катушки.
Энергия контура с индуктивностью
2
LI
L, по которому течёт ток I (при
Wм
2
отсутствии ферромагнетиков):
[11]

20.

ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ
Найдём энергию магнитного поля идеального
соленоида:
2
B
0 IN
l
0 N S
L
l
2
2
1 0 N S Bl
Wм
2
l
0 N
B2
2 0
Sl
B2
2 0
V
V = Sl – объем соленоида.
dWм
Объёмная плотность энергии: м
dV
2
B
1
2
м
0 H [12]
2 0
2