Угол между прямыми в пространстве

1. Угол между прямыми в пространстве.

Учитель математики школы
№341
Паничева Марина
Владимировна

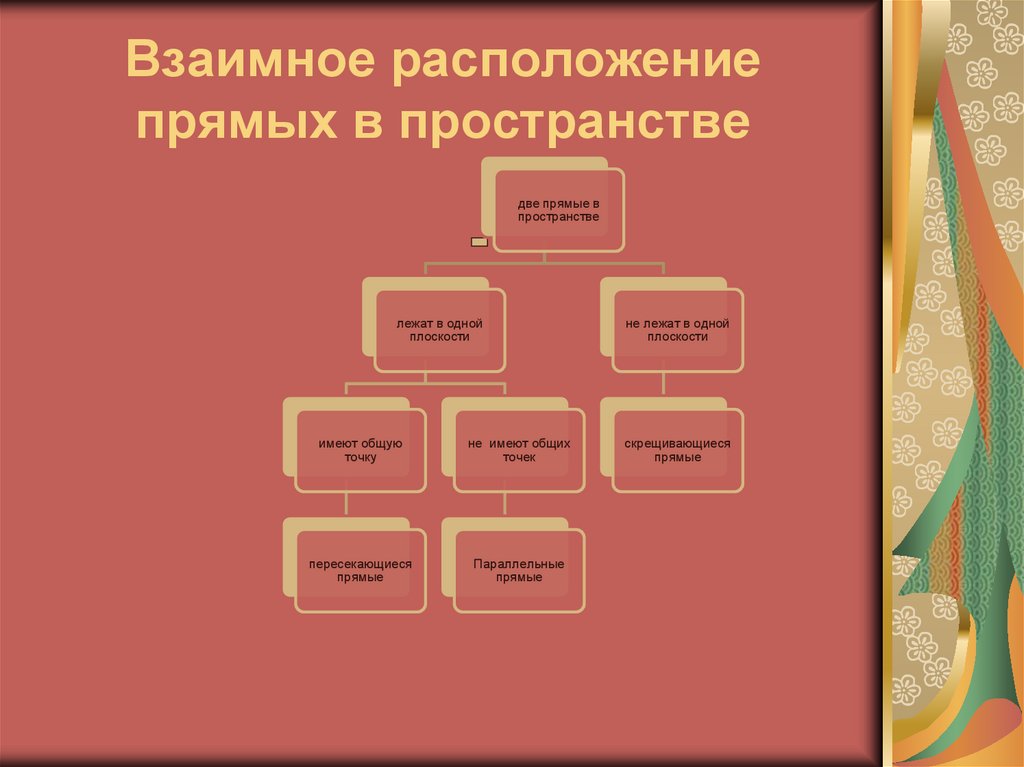
2. Взаимное расположение прямых в пространстве

две прямые в
пространстве
лежат в одной
плоскости
имеют общую
точку
не имеют общих
точек
пересекающиеся
прямые
Параллельные
прямые
не лежат в одной
плоскости
скрещивающиеся
прямые

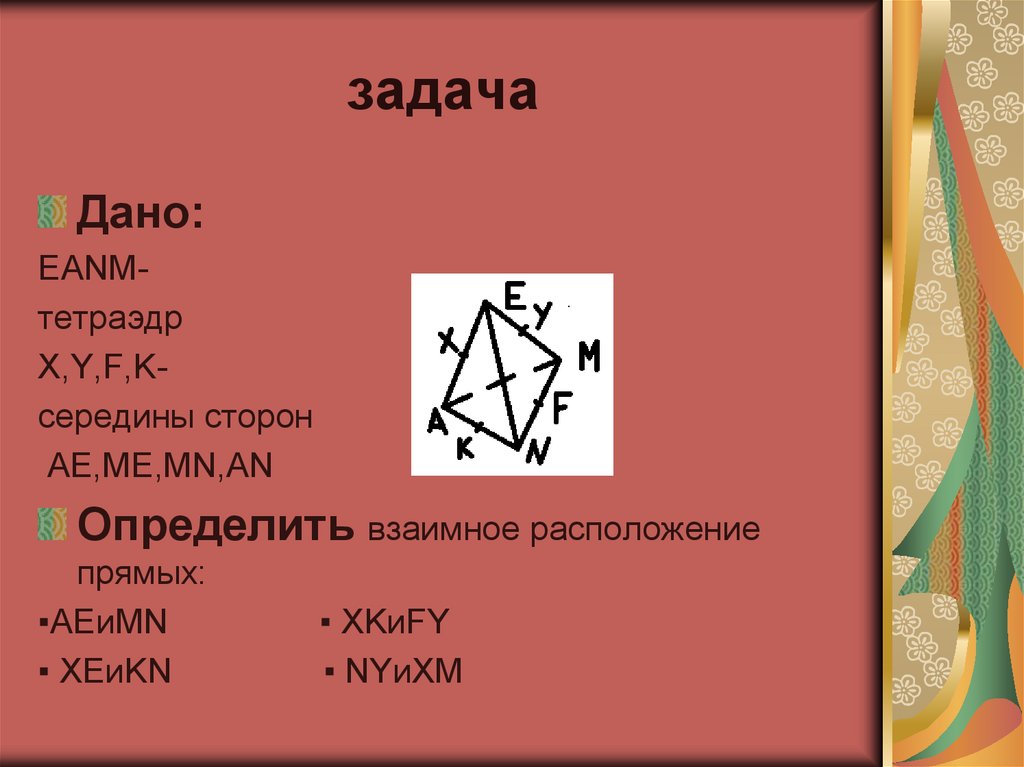
3. задача

Дано:
EANMтетраэдр
X,Y,F,Kсередины сторон
AE,ME,MN,AN
Определить взаимное расположение
прямых:
▪AEиMN
▪ XEиKN
▪ XKиFY
▪ NYиXM

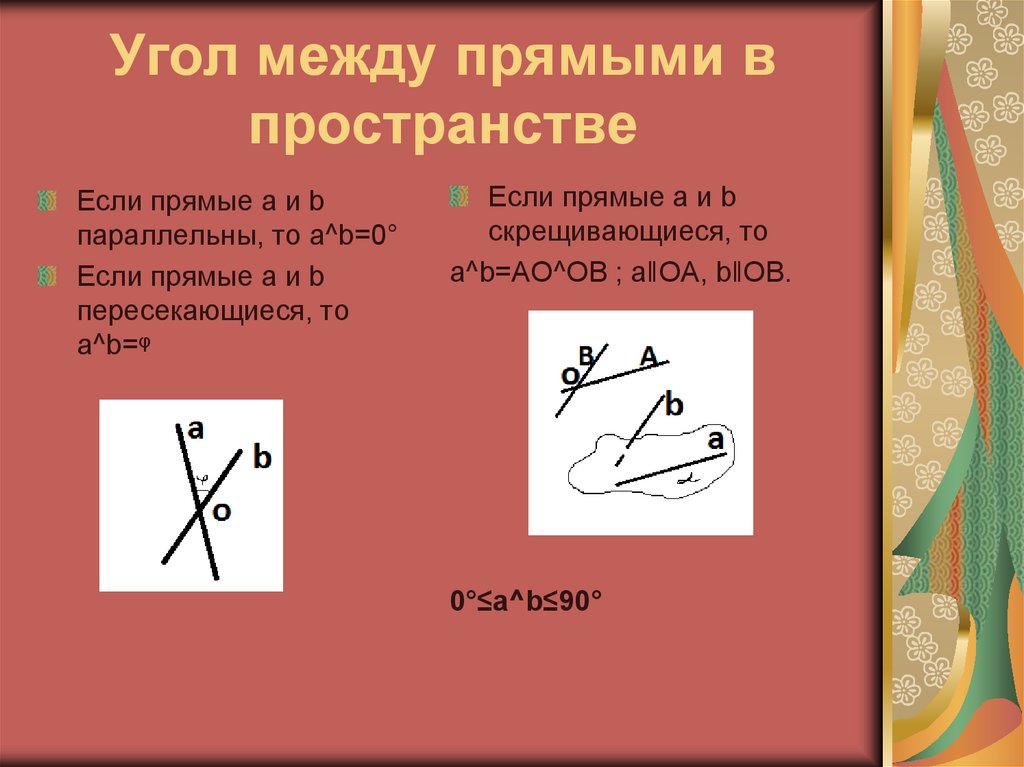
4. Угол между прямыми в пространстве

Если прямые a и b
параллельны, то a^b=0°
Если прямые a и b
пересекающиеся, то
a^b=ᵠ
Если прямые a и b
скрещивающиеся, то
a^b=AO^OB ; aǁOA, bǁOB.
0°≤a^b≤90°

5. задача

Дано:
a¢плABC
aǁAB
MN-средняя линия∆ABC
∟A=25°, ∟B=100°.
Найти:
▪a^MN
▪a^BC
▪a^AC
▪AC^BC

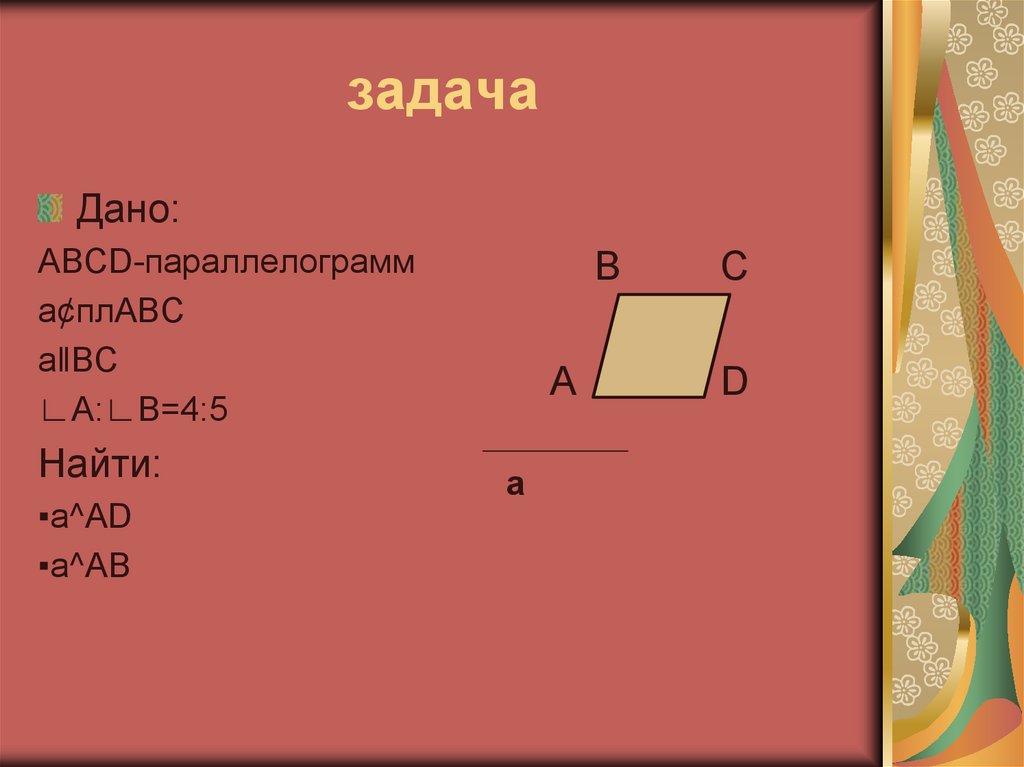
6. задача

Дано:
ABCD-параллелограмм
a¢плABC
aǁBC
∟A:∟B=4:5
Найти:
▪a^AD
▪a^AB
B
A
a
C
D

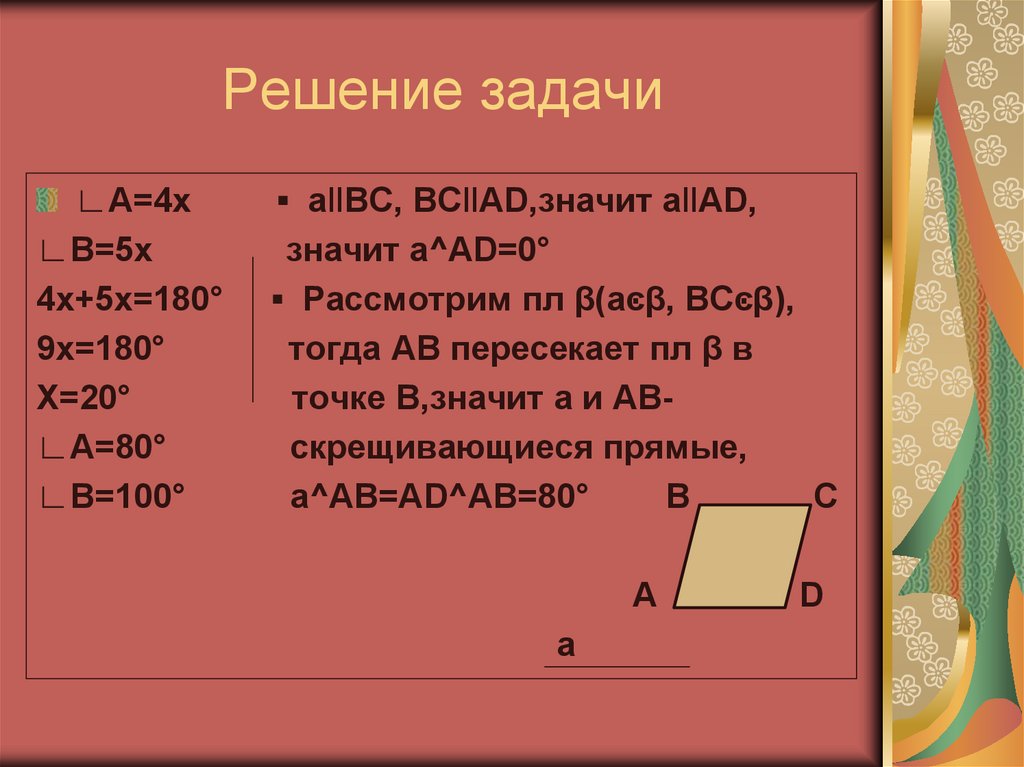
7. Решение задачи

∟A=4x
∟B=5x
4x+5x=180°
9x=180°
X=20°
∟A=80°
∟B=100°
▪ aǁBC, BCǁAD,значит aǁAD,
значит a^AD=0°
▪ Рассмотрим пл β(aͼβ, BCͼβ),
тогда AB пересекает пл β в
точке B,значит a и ABскрещивающиеся прямые,
a^AB=AD^AB=80°
B
C
A
a
D

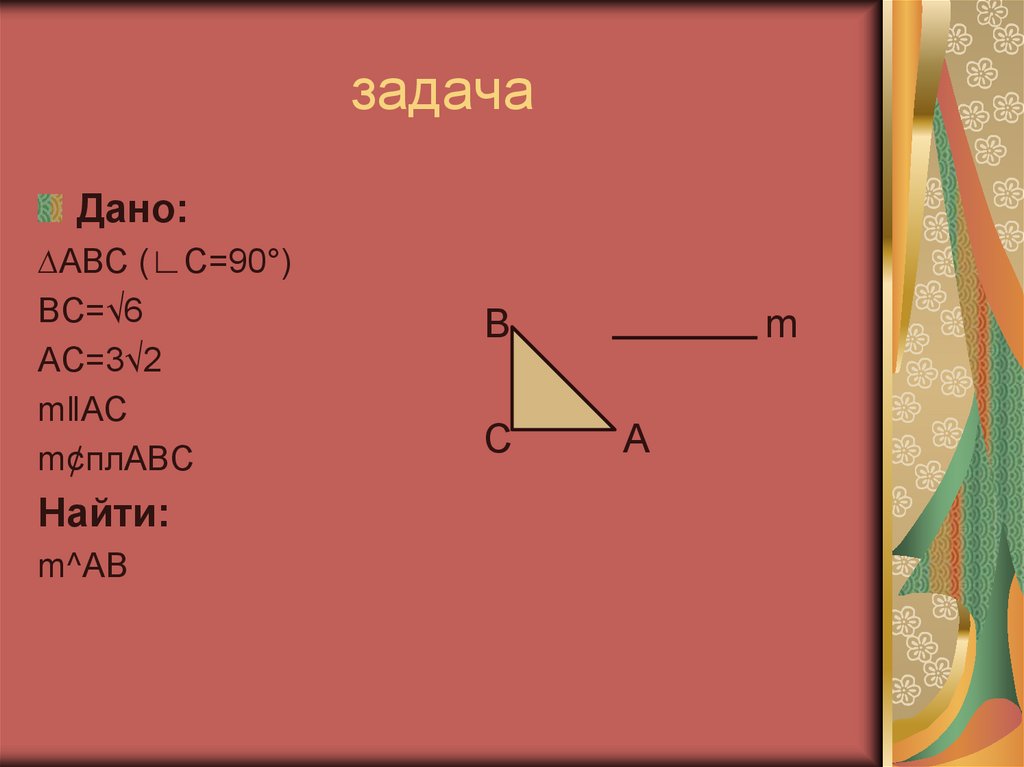
8. задача

Дано:
∆ABC (∟C=90°)
BC=√6
AC=3√2
mǁAC
m¢плABC
Найти:
m^AB
B
C
m
A

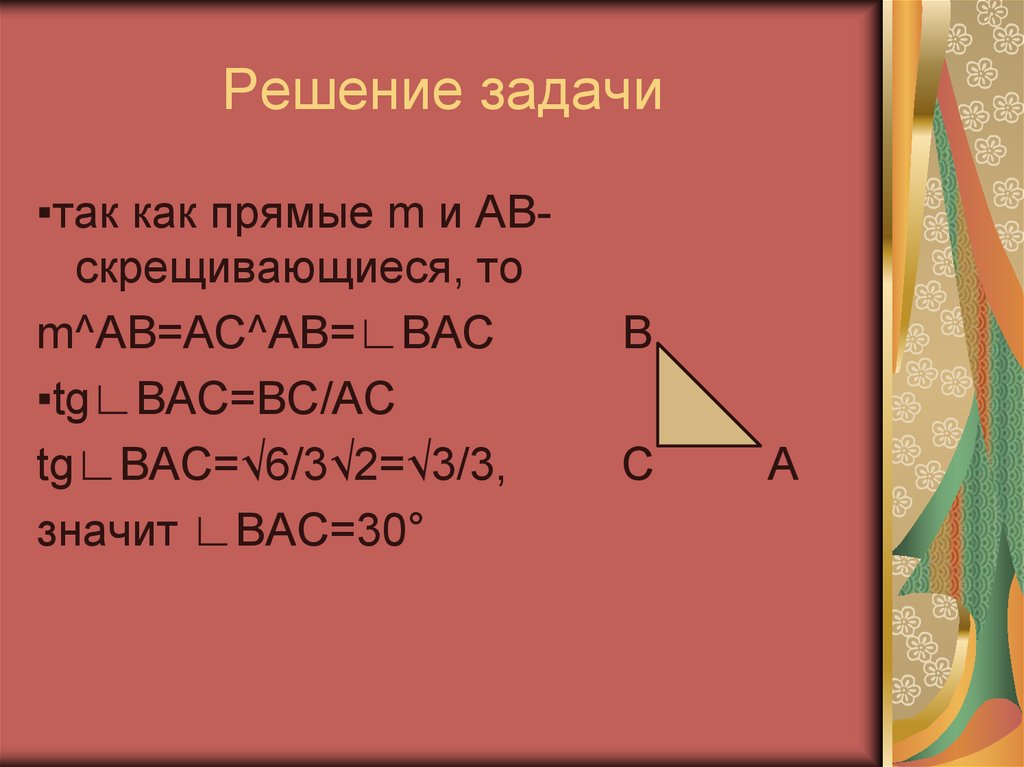
9. Решение задачи

▪так как прямые m и ABскрещивающиеся, то
m^AB=AC^AB=∟BAC
▪tg∟BAC=BC/AC
tg∟BAC=√6/3√2=√3/3,
значит ∟BAC=30°
B
C
A

10. Домашнее задание

п.9 №45(б), №46(а).