Похожие презентации:
Теория механизмов и машин слайд-лекции для студентов технических специальностей. Лекция 1
1.
Теория механизмов и машинслайд-лекции для студентов
технических специальностей
2.
ЛЕКЦИЯ 1Краткое содержание
• Введение.
• Цель и задачи курса ТММ.
•Краткая историческая справка.
•Основные определения курса ТММ.
•Машина. Классификация машин.
• Механизм. Классификация механизмов.
•Машинный агрегат.
•Элементы механизма: звено, кинематическая пара,
кинематическая цепь. Их классификация.
3.
Цель и задачи курсаТеория механизмов и машин - это наука, изучающая
структуру, кинематику и динамику механизмов и
машин в связи с их анализом и синтезом.
К основным задачам теории механизмов и машин
относятся:
• изучение строения (структуры) механизма;
• определение положений механизмов и траекторий,
описываемых отдельными точками;
• определение скоростей и ускорений отдельных точек и
звеньев механизма;
• исследование
и
проектирование
различных
механизмов: рычажных, зубчатых, кулачковых;
4.
• определение различных сил, действующих назвенья механизма (внешних, реакций, трения,
инерции);
• изучение способов уравновешивания сил инерции в
машинах, балансировка роторов;
• изучение энергетического баланса машин (к.п.д. и
др.);
• изучение истинного закона движения машин под
действием заданных сил и способов регулирования
скорости машины.
5.
Краткая историческая справкаКак самостоятельная научная дисциплина ТММ,
подобно другим прикладным разделам науки, возникла в
результате промышленной революции, начало которой
относится к 30-м годам XVIII века. Однако машины
существовали задолго до этой даты. Поэтому в истории
развития ТММ можно условно выделить четыре периода.
1-й период до начала XIX века - период эмпирического
машиностроения, в течении которого изобретается
большое количество простых машин и механизмов:
подъемники, мельницы, камнедробилки, ткацкие и
токарные станки, паровые машины (Леонардо да Винчи,
Вейст, Ползунов, Уатт).
6.
Одновременно закладываются и основы теории: теоремаоб изменении кинетической энергии и механической
работы, "золотое правило механики", законы трения,
понятие
о
передаточном
отношении,
основы
геометрической теории циклоидального и эвольвентного
зацепления (Карно, Кулон, Амонтон, Кадано, Ремер,
Эйлер).
2-й период от начала до середины XIX века - период
начала развития ТММ. В это время разрабатываются такие
разделы как кинематическая геометрия механизмов
(Савари, Шаль, Оливье), кинетостатика (Кариолис), расчет
маховика (Понселе), классификация механизмов по
функции преобразования движения (Монж, Лану) и другие
разделы. Пишутся первые научные монографии по
механике машин (Виллис, Бориньи), читаются первые
курсы лекций по ТММ и издаются первые учебники
(Бетанкур, Чижов, Вейсбах).
7.
3-й период от второй половины XIX века до начала XXвека - период фундаментального развития ТММ. За этот
период разработаны: основы структурной теории
(Чебышев, Грюблер, Сомов, Малышев), основы теории
регулирования машин (Вышнеградский), основы теории
гидродинамической
смазки
(Грюблер),
основы
аналитической теории зацепления (Оливье, Гохман),
основы графоаналитической динамики (Виттенбауэр,
Мерцалов), структурная классификация и структурный
анализ (Ассур), метод планов скоростей и ускорений (Мор,
Манке), правило проворачиваемости механизма (Грасгоф)
и многие другие разделы ТММ.
8.
4-й период от начала XX века до настоящего времени период интенсивного развития всех направлений ТММ какв России, так и за рубежом. Среди русских ученых
необходимо
отметить
обобщающие
работы
Артоболевского И.И., Левитского Н.И., Фролова К.В.; в
области структуры механизмов - работы Малышева А.И.,
Решетова Л.П., Озола О.Г.; по кинематике механизмов работы Колчина Н.И., Смирнова Л.П., Зиновьева В.А.; по
геометрии зубчатых передач - работы Литвина Ф.Л.,
Кетова Х.Ф., Гавриленко В.А., Новикова М.Л.; по
динамике машин и механизмов - Горячкина В.П.,
Кожевникова С.П., Коловского М.З. и др. Данное
перечисление не охватывает и малой доли работ
выдающихся ученых, внесших существенный вклад в
развитие ТММ в этот период. Из зарубежных ученых
необходимо отметить работы Альта X., Бегельзака Г.,
Бейера Р., Крауса Р., Кросли Ф. и многих других.
9.
Основные определения курса ТМММашина
По мере развития машин содержание термина "машина"
изменялось. Для современных машин дадим следующее
определение:
Машина есть устройство, создаваемое человеком для
преобразования энергии, материалов и информации с
целью облегчения физического и умственного труда,
увеличения его производительности и частичной или
полной замены человека в его трудовых и
физиологических функциях.
10.
Классификация машин1.Энергетические машины (электродвигатели, ДВС,
компрессоры и т.д.);
2.Транспортные машины (краны, конвейеры, автомобили
и т.д.);
3.Технологические машины (металлорежущие станки,
полиграфические, горнодобывающие, швейные машины и
др.);
4.ЭВМ.
11.
МеханизмСуществует несколько определений. Дадим одно из них.
Механизм есть система тел, предназначенная для
преобразования движения одного или нескольких
твердых тел в требуемые движения других тел.
Все механизмы можно разделить на плоские и
пространственные.
У плоского механизма точки его звеньев описывают
траектории, лежащие в параллельных плоскостях.
У пространственного механизма точки его звеньев
описывают неплоские траектории или траектории,
лежащие в пересекающихся плоскостях.
12.
Классификация механизмов (по конструктивнымпризнакам)
1.Рычажные механизмы (рис.1.1).
Рычажные механизмы являются основными в различных
машинах. Например, в строгальных станках они
выполняют основную рабочую операцию - строгание
заготовки, преобразуя вращательное движение вала в
возвратно-поступательное движение резца; в ДВС преобразуют
возвратно-поступательное
движение
поршней во вращательное движение главного вала, в
штамповочной машине - осуществляют срез материала.
13.
Рис.1.1а).
б).
в).
14.
Средиэтого
типа
механизмов
наибольшее
распространение
получили
плоские
рычажные
четырехзвенные механизмы (рис.1.1,а, б, в). На рис.1.1,а
показан кривошипно-ползунный механизм, который
используется для преобразования вращательного движения
кривошипа ОА в возвратно-поступательное движение
ползуна В. Ползун и кривошип соединяются с помощью
звена АВ (шатуна), совершающего плоскопараллельное
движение. Механизм, показанный на рис.1.1,б, называют
кривошипно-коромысловым механизмом. Его ведущее
звено О1А кривошип совершает полнооборотное
вращение, звено АВ шатун - плоскопараллельное
движение, а ведомое звено ВО2 коромысло –
неполнооборотное вращение. На рис.1.1,в показан
кривошипно-кулисный
механизм,
состоящий
из
кривошипа О1А, кулисы АО2, представляющей собой
подвижное направляющее звено, по которому движется
кулисный камень.
15.
2.Кулачковые механизмы (рис. 1.2).Кулачковые механизмы образуются путем силового
замыкания кулачка и толкателя. Кулачок 1 обычно
представляет собой диск, профиль которого очерчен
определенной кривой, которая задает движение толкателю
2. Для уменьшения потерь на трение толкатель снабжают
цилиндрическим роликом.
Механизмы
используют
для
преобразования
вращательного (рис.1.2,а) или возвратно-поступательного
(рис.1.2,б) движения кулачка в возвратно-поступательное
движение толкателя. Применяют также сложные
пространственные механизмы (рис.1.2,в).
Используются: в строгальных и долбежных станках для
поперечного перемещения стола с обрабатываемой
деталью,
в
ДВС
для
открытия
клапанов
(распределительный вал).
16.
а).б).
в).
Рис.1.2
17.
3.Зубчатые механизмы (рис.1.3).Зубчатые механизмы образуются зубчатыми колесами.
Передача нагрузки и движение осуществляется за счет
воздействия зубьев друг на друга.
Их используют в большинстве механизмов для передачи
энергии от двигателя к ведущим валам.
18.
Рис.1.319.
4.Фрикционные механизмы (рис.1.4).Во фрикционных механизмах движение передается за
счет сил трения, возникающих при контакте звеньев.
Простейшая фрикционная передача (рис.1.4,а) состоит из
двух цилиндрических катков 1 и 2 и стойки 3. Один каток
прижимается к другому с помощью пружины.
Используются в кинематических цепях приборов для
обеспечения плавности движения, бесшумности и
безударного включения. К фрикционным механизмам
относятся и вариаторы (рис.1.3,б), которые обеспечивают
плавное изменение угловой скорости ведомого звена 2 при
равномерном вращении ведущего звена 1 и его
перемещения вдоль оси.
20.
а).б).
Рис.1.4
21.
5.Гидравлические, пневматические механизмы (рис.1.5).В этих механизмах для преобразования движения кроме
твердых тел участвуют жидкие или газообразные тела. На
рис.1.5 приведена схема гидравлического механизма,
предназначенного для привода в движение поршня 1 с
помощью распределителя 2. Жидкость в цилиндр 5
поступает из распределителя в результате поочередного
включения электромагнитов 3 и 4. Гидравлическая схема
включает в себя также насос 6, бак 7 и клапан 8. В
пневматических механизмах насос заменяют источником
сжатого воздуха.
22.
Рис.1.6Рис.1.5
23.
6.Механизмы с гибкими звеньями (рис.1.6).Данные
механизмы
применяют
для
передачи
вращательного движения на большие расстояния с
преобразованием параметров вращения.
Передача движения осуществляется за счет сил трения.
В качестве гибких звеньев применяют ремни, канаты,
цепи, нити.
24.
7.Клиновые механизмы (рис.1.7).Рис.1.7
Простейший клиновой механизм состоит из клиньев 2, 3
и стойки 1. Он служит для преобразования одного
прямолинейного движения в другое. Эти механизмы
применяются различного вида прессов, поглощающих
аппаратов железнодорожных автосцепок, зажимов,
механизмов подачи деталей и т.д..
25.
Машинный агрегат – это совокупностьвзаимосвязанных механизмов.
ПМ
Передаточный механизм
ИМ
Исполнительный механизм
Рабочий
орган
Двигатель
Блок-схема машинного агрегата
Звено
Звено - это одна или несколько деталей механизма,
соединенных между собой жестко.
26.
В каждом механизме имеется 4 группы звеньев.1.Неподвижное звено - стойка. Стойка в механизме
может быть только одна, так как все неподвижные
звенья являются единым целым (например, корпус
электродвигателя, станина станка) Условное
обозначение (рис.1.8, звено 6).
2.Подвижные звенья.
3.Ведущие звенья – это звенья, закон движения
которых задан.
4.Ведомые звенья - это звенья, закон движения
которых определяется движением ведущих звеньев.
Ведущие и ведомые звенья являются подвижными.
27.
В рычажных механизмах имеются следующиеподвижные звенья:
кривошип (рис.1.8, звено 1), совершает полный оборот
относительно стойки;
коромысло (рис.1.8, звено 5), совершает неполный
оборот относительно стойки;
ползун (рис.1.8, звено 2), совершает возвратнопоступательное движение;
кулиса (рис.1.8, звено 3), звено, которое совершает
вращательное движение относительно стойки и на котором
есть направляющая для ползуна;
шатун (рис 1.8, звено 4) - звено, которое не имеет
соединения со стойкой.
28.
Рис. 1.829.
Кинематическая параКинематическая пара - это соединение двух звеньев,
обеспечивающее перемещение одного звена
относительно другого.
Кинематические пары передают нагрузку и движение и
часто определяют работоспособность и надежность
механизма и машины в целом. Поэтому правильный выбор
вида пары, ее формы и размеров, а также
конструкционных материалов и условий смазывания имеет
большое значение при проектировании и эксплуатации
машин.
Кинематические пары классифицируются по следующим
признакам:
а).по числу степеней подвижности Н
Возможные независимые движения одного звена
относительно другого называются степенями
подвижности кинематической пары H.
30.
Ограничения, накладываемые на относительныедвижения звеньев, называются условиями связи в
кинематических парах.
Число степеней подвижности кинематической пары
определяется зависимостью
H=6-S(1.1)
где 6-максимальное число степеней свободы твердого
тела в пространстве (3 поступательных и 3 вращательных
движения относительно осей координат XYZ);
S-число условий связи, наложенных кинематической
парой на относительное движение каждого звена.
Кинематические пары делятся на: одноподвижные
(поступательные, вращательные, винтовые),
двухподвижные, (кулачек-толкатель, зуб-зуб),
трехподвижные, (сферические), четырёхподвижные,
(цилиндр-плоскость), пятиподвижные (шар-плоскость).
Примеры приведены в таблице1.1.
31.
б).по характеру соприкосновения звеньевкинематические пары делятся на низшие и высшие
Низшими кинематическими парами называются
такие, в которых соприкосновение звеньев происходит
по поверхности.
Например, одноподвижные поступательная и
вращательная кинематические пары,
Высшими называются такие кинематические пары, у
которых соприкосновение звеньев происходит по линии
или точке.
Например, кинематические пары зуб-зуб, кулачектолкатель (рис.1.2, 1.3).
Так как в низших кинематических парах звенья
соприкасаются по поверхностям, то удельное давление в
них невелико, вследствие чего износ в низших
кинематических парах невелик.
32.
В местах контакта высших кинематических пар удельноедавление очень велико, что вызывает их повышенный
износ. Это большой недостаток высших кинематических
пар по сравнению с низшими.
Однако они имеют и большое преимущество: если
количество низших пар ограничено, то высших пар
большое разнообразие, их количество практически не
ограничено. Поэтому при помощи высших
кинематических пар значительно проще создать
механизмы, обеспечивающие заданный закон движения.
в).по характеру относительного движения
33.
Виды кинематических пар приведены в таблице 1.1.В – вращательная (Н=1), П – поступательная (Н=1), ВП –
цилиндрическая (Н=2); ВВВ – сферическая (Н=3), ВВП –
шар-цилиндр с прорезью (Н=3), ВПП – плоскостная (Н=3),
ВВВП – шар-цилиндр (Н=4), ВВПП – цилиндр-плоскость
(Н=4), ВВВПП – шар-плоскость (Н=5). Здесь буква «В»
обозначает возможное вращательное движение, «П» возможное поступательное движение.
34.
Таблица 1.135.
Кинематические цепиКинематическая цепь - это система звеньев,
соединённых с помощью кинематических пар.
Классификация кинематических цепей
Незамкнутые - это такие кинематические цепи,
которые имеют звенья, входящие только в одну
кинематическую пару (рис.1.10).
Замкнутые - это кинематические цепи, в которых
каждое звено входит не менее, чем в две
кинематические пары (рис.1.11).
Простые - это кинематические цепи, в которых
каждое звено входит не более, чем в две
кинематические пары (рис.1.10, 1.11).
Сложные - это кинематические цепи, в которых
имеется хотя бы одно звено, входящее более чем в две
кинематические пары (рис.1.12).
Большинство используемых механизмов образованы
замкнутыми кинематическими цепями.
36.
Рис.1.12Рис.1.10
Рис.1.11
37.
ЛЕКЦИЯ 2Краткое содержание
1.Структурная схема механизма.
2.Кинематическая схема механизма.
3.Определения степени подвижности механизма.
Структурный принцип образования механизмов.
Начальный механизм.
4.Группы Ассура.
5.Структурный анализ механизма. Примеры.
38.
Структурная схема механизма – это безмасштабноеграфическое изображение механизма с применением
условных обозначений звеньев и кинематических пар.
Кинематическая схема механизма – это структурная
схема, выполненная в масщтабе.
Степень подвижности механизмов
Степень подвижности механизма W - это количество
независимых движений, которые нужно подвести к
механизму, чтобы на выходе получить одно или
наоборот.
Для плоских механизмов применяется формула
Чебышева:
W = 3n - 2p1 -p2,
(2.1)
где n – число подвижных звеньев механизма;
p1 - число одноподвижных кинематических пар;
p2 - число двухподвижных кинематических пар.
39.
В пространственных механизмах степень подвижностиопределяется по формуле Сомова-Малышева:
W = 6n - 5p1 - 4p2 - 3p3 - 2p4 - p5,
(2.2)
где р3 - число трёхподвижных кинематических пар;
р4 - число четырёхподвижных кинематических пар;
р5 - число пятиподвижных кинематических пар.
Большинство механизмов имеют степень подвижности
W=1. Их называют рациональными. Эти механизмы не
чувствительны к погрешностям монтажа, изготовления и
деформирования. Такие механизмы не требуют
приработки.
У дифференциальных зубчатых механизмов W=2, у
роботов и манипуляторов W=4-8, у основного механизма
экскаватора W=4. Если W=0, то получим неподвижную
конструкцию – ферму.
40.
Структурный принцип образования механизмов.Группы Ассура
Основной принцип образования механизмов был
впервые сформулирован в 1916 году русским учёным
Леонидом Владимировичем Ассуром - профессором
Петербургского политехнического института.
Согласно идее Л.В.Ассура любой механизм образуется
последовательным присоединением к ведущим звеньям и
стойке кинематических цепей, удовлетворяющих условию,
что степень их подвижности W=0.
Ведущее звено, входящее в одноподвижную
кинематическую пару со стойкой образует начальный
механизм. (рис.2.1 а, б).
Ведущим звеном может быть как кривошип, так и
ползун. Начальному механизму присваивается 1 класс.
Степень подвижности начального механизма W =1.
41.
а).б).
Рис.2.1
42.
Кинематические цепи, у которых степеньподвижности W=0, называются группами Ассура.
=
+
+
Начальный
механизм
1 класс
Группа Ассура
Группа Ассура
II класс
Механизм
II класс
43.
Виды групп Ассура II классаРассмотрим кинематические цепи, в состав которых
входят только одноподвижные кинематические пары.
Для группы Ассура
W 3 n 2 p1 0 или
3
p1
n
2
(2.3)
Так как количество кинематических пар должно быть
целыми, то количество звеньев группы Ассура может быть
только чётными числом. Следовательно, равенству (2.1)
может удовлетворить следующий ряд чисел:
n (количество подвижных звеньев )
2 4 6
p1 (число одноподвижных пар )
3 6 9
Класс группы Ассура
II III IV
и т.д.
44.
В группу Асура II класса может входить: 2 подвижныхзвена и 3 кинематические пары, которые необходимы для
присоединения звеньев к стойке или к другим звеньям.
Если обозначить вращательную кинематическую пару В, а
поступательную П, то возможны следующие виды групп
Ассура II класса:
1.ВВВ (рис.2.2); 2. ВВП (рис.2.3); 3.ВПВ (рис.2.4); 4.ПВП
(рис.2.5); 5.ППВ (рис. 2.6).
Рис.2.2
Рис.2.3
Рис.2.4
45.
Рис.2.5Рис.2.6.
Казалось бы, что, следуя по пути замены вращательных пар
поступательными, можно было бы заменить все три
вращательные пары поступательными (ППП). Но в этом
случае при присоединении к стойке эта группа Ассура будет
переходить в плоский механизм с одними поступательными
парами - клиновой механизм (рис.1.7).
46.
В группах Ассура различают внутренние и внешниекинематические пары.
Число внешних пар, которыми группа присоединяется
к не относящимся к ней звеньям механизма или стойке,
называют порядком группы.
Все группы Ассура П класса являются группами второго
порядка.
Класс механизма определяется наивысшим классом
Ассура, которая входит в его состав.
Структурный анализ механизма
Задачей структурного анализа механизма является определение параметров структуры заданного механизма:
числа звеньев, числа и вида кинематических пар,
определение степени подвижности механизма, разбиение
механизма на группы Ассура и начальный механизм,
определение класса всего механизма.
47.
Алгоритм проведения структурного анализа1.Начертить структурную схему механизма.
2.Обозначит все подвижные и неподвижные звенья
механизма. Начать обозначение с ведущего звена–
кривошипа и далее по порядку. Найти количество
подвижных звеньев п.
3.Заглавными буквами латинского алфавита обозначить
все
кинематические
пары.
Найти
количество
кинематических пар p1 и р2.
4.Определить степень подвижности механизма.
5.Отсоединить от механизма наиболее отдаленную от
ведущего звена группу Ассура II класса, так чтобы
оставшийся механизм продолжал работать, а степень его
подвижности W не менялась. Определить вид, порядок,
класс и степень подвижности данной группы Ассура.
Записать структурную формулу группы Ассура.
48.
6.Продолжать отсоединять от механизма группыАссура до тех пор, пока не останется начальный
механизм.
7.Определить класс и степень подвижности
начального механизма. Записать структурную формулу
начального механизма.
8.Записать структурную формулу всего механизма.
9.Определить класс механизма.
49.
ПРИМЕР 2.1Выполнить структурный анализ механизма.
1.Структурная схема механизма.
50.
2.Звенья механизма№
звена
1
2
3
4
5
6
Наименовани
е
Подвижност
ь
Число
звеньев
подвижных
51.
3.Кинематические парыЧисло одноподвижных кинематических пар p1=7,
число двух подвижных кинематических пар р2=0.
4.Степень подвижности механизма
5.Строение групп Асcура
а).Последняя группа Асcура
б).Предпоследняя группа Асcура
в).Начальный механизм
6.Структурная формула всего механизма
7.Класс всего механизма II, так как наивысший класс
группы Ассура, входящей в данный механизм II.
52.
ЛЕКЦИЯ 3Краткое содержание
1.Определение скоростей и ускорений точек звеньев при
поступательном, вращательном и плоскопараллельном
движениях.
2.Планы скоростей и ускорений.
3.Принцип подобия в планах скоростей и ускорений.
4.Примеры кинематического исследования механизмов.
53.
Теоретические предпосылки определения скоростейи ускорений
Основные формулы для определения скоростей и
ускорений точек звеньев механизмов приведены в таблице
3.1.
Планы скоростей и ускорений
Планом скоростей (ускорений) называется диаграмма,
на которой от некоторого центра (полюса) в масштабе
отложены векторы скоростей (ускорений) точек тела.
Рассмотрим тело, совершающее плоскопараллельное
движение (рис.3.1).
Для плоскопараллельного движения скорости точек
определяются по формулам:
VB V A VBA
,
VB VC VBC
,
VC VA VCA
(3.1)
54.
где- абсолютные скорости точек А, В, С;
V
V
V A, B , C
VBA
V
BC
,
- относительные скорости.
V
CA
,
План скоростей получим, если в выбранном масштабе
V
(
м/с )
мм
отложим от полюса
pV
отрезки
pV a
pV b и pV c , параллельные векторам скоростей V A ,
VB
, VC
55.
Отрезки находятся по формулам:pV a
VA
pV b
VB
pV c
VC
V
V
V
56.
Сформулируем принцип подобия в планескоростей:
В плане скоростей векторы относительных
скоростей точек жесткого звена образуют фигуру,
подобную звену, повернутую на угол 90° в сторону
угловой скорости звена.
Следствие.
Пользуясь принципом подобия, достаточно на плане
скоростей построить векторы скоростей только двух
точек жесткого звена. Скорость же любой третьей точки
определится путем построения фигуры или линии
подобной данному звену.
Аналогично формулируется принцип подобия в плане
ускорений.
57.
Основные формулы для определения скоростей иускорений точек звеньев
а
Таблица
3.1
n
ВА
№
Вид движения
1
Поступательное
(ползун по стойке)
Скорость
Все точки звена
имеют одинаковую
скорость , вектор
который направлен
вдоль траектории
движения точки A.
II Х-Х
Ускорение
Все точки звена
имеют одинаковые
ускорения . Если вектор
ускорения направлен в
сторону , то движение
равноускоренное, если
вектор ускорения
направлен в
противоположнyю
сторону , то движение
равнозамедленное.
II Х -Хx
58.
2Вращательное вокруг
Скорость точки А
неподвижной оси
Вектор направлен
(кривошип или коромысло перпендикулярно ОА,
относительно стойки)
в сторону угловой
скорости .
Полное ускорение точки
А
Нормальное ускорение =
Вектор направлен по
радиусу АО к центру
вращения О.
II OA.
Касательное ускорение
Вектор направлен
перпендикулярно АО в
сторону углового ускорения
59.
3Звено совершает
плоскопараллельное движение
(шатун)
Скорость точки В
Ускорение точки В
Относительная
Относительное
скорость
ускорение
Вектор направлен
Нормальное ускорение
перпендикулярно к
=
ВА в сторону
Вектор направлен
угловой скорости .
параллельно АВ (от точки
В к точке А)
II ВА
Касательное ускорение
Вектор направлен
перпендикулярно АВ
ВА
60.
Пример 3.1Кинематический расчёт кривошипно-ползунного
механизма. Определение скоростей точек звеньев для
заданного положения механизма.
Дано:
1).Угловая скорость кривошипа является постоянной и
равна
1 30с 1
.
2).Размеры звеньев:
ОА = 20мм, АВ = 76мм, ВС = 26мм.
61.
План скоростейм/с
v 0,01
мм
62.
Исследуемая
величина
VA
VB
Отрезок
на плане
pV a V A OA
pV b V B // X X
VBA ab
VC pV c
2
Направление
VBA BA
Величи
Масштабны
на
й
отрезка
коэффициент
на плане,
μv
мм
м/с
0,01
мм
Значение
величины,
м/с
63.
1. Определение скорости точки А..
V A 1 O A 30 0,02 0,6 м / с
Вектор скорости V
перпендикулярен кривошипу ОА.
A
Выбираем масштаб плана скоростей
м/c
V 0,01
мм
Найдём отрезок, изображающий вектор скорости
VA
на плане:
64.
VA0,6
pV a
60 мм
V 0,01
Из полюса плана скоростей pV
откладываем
данный
отрезок
в
направлении,
перпендикулярном ОА в направлении угловой скорости
1
2. Определение скорости точки В.
Запишем векторное уравнение:
VB V A VBA
.
Направления
векторов скоростей:
VB ВО 2 VBA BA
Продолжим строить
план скоростей.
Из конца вектораV A (точка a )проводим направление
вектора V
.
BA
65.
Из полюса (точкаpV
проводим направление вектора V B
)
На пересечении двух проведённых направлений получим точку . b
Измеряя длины полученных отрезков и умножая их на масштаб
V , получим значения скоростей:
VB pV b V
VBA ab V
3. Определение скорости точки С.
Воспользуемся следствием из теоремы подобия. Составим
пропорцию:
ab BC
AB ab
, bc
BC bc
AB
мм
66.
Данный отрезок откладываем на продолжении отрезка ab .Точку c соединяем с полюсом pV
Величина скорости точки С:
.
VC pV c V
4. Определение угловой скорости шатуна АВ.
VBA
2
AB
с-1
Для определения направления 2
переносим вектор VBA
в точку В шатуна АВ и смотрим как она движется относительно
точки А. Направление этого движения соответствует
2
В данном случае угловая скорость 2 направлена
против
часовой стрелки.
67.
Пример 3.2Кинематический
расчёт
кривошипно-коромыслового
механизма. Определение скоростей точек звеньев для заданного
положения механизма.
Дано:
1).Угловая скорость кривошипа является постоянной и равна
1 30с 1
2).Размеры звеньев:
О1А = 20 мм, АВ = 50 мм, ВО2 = 30 мм, ВС = 25 мм.
68.
План скоростейм/с
v 0,01
мм
69.
Исследуемая
величина
VA
VB
Отрезок
на плане
pV a V A OA
pV b V B // X X
VBA ab
VC pV c
2
3
Направление
VBA BA
Величи
Масштабны
на
й
отрезка
коэффициент
на плане,
μv
мм
м/с
0,01
мм
Значение
величины,
м/с
70.
1. Определение скорости точки А.VA 1 O1 A 30 0,02 0,6 м / с
Вектор скорости V A перпендикулярен кривошипу О1А.
Выбираем масштаб плана скоростей 0,01 м / c
V
мм
Найдём отрезок изображающий вектор скорости
на плане:
VA
VA
0,6
pV a
60 мм
V 0,01
Из полюса плана скоростей pV откладываем данный отрезок
в направлении, перпендикулярном О1А в направлении угловой
скорости
1.
71.
2. Определение скорости точки В.Запишем векторное уравнение: VB V A VBA
Направления векторов скоростей: VB ВО 2 ,
VBA BA
Продолжим строить план скоростей.
Из конца вектора V проводим направление вектора V .
A
BA
Из полюса pV проводим направление вектора V .
B
На пересечении двух проведённых направлений получим точку
Измеряя длины полученных отрезков и умножая их на масштаб
, получим значения скоростей:
V
VBA ab V
VB pV b V
b
72.
3. Определение скорости точки С.Воспользуемся следствием из теоремы подобия. Составим
пропорцию:
AB ab
,
BC bc
ab ВC
bc
АB
Данный отрезок откладываем на продолжении отрезка ab .
Точку c соединяем с полюсом
pV.
.
Величина скорости точки С:
VC pV c V
73.
4. Определение угловой скорости шатуна АВ.VBA
2
AB
Для определения направления 2 переносим вектор VBA
в точку В шатуна АВ и смотрим как она движется относительно
точки А. Направление этого движения соответствует
2
В данном случае угловая скорость 2
часовой стрелки.
направлена
5. Определение угловой скорости коромысла ВО2.
VB
3
BO 2
против
74.
Для определения направления3 переносим вектор V
B
.
в точку В коромысла ВО2 и смотрим как она движется
относительно точки О2. Направление этого движения соответствует
3 . В данном случае угловая скорость 3 направлена против
часовой стрелки.
Пример 3.3
Кинематический расчёт кривошипно-ползунного механизма.
Определение ускорений точек звеньев для заданного положения
механизма.
Дано:
1).Угловая скорость кривошипа является постоянной и равна
1 30с
1
75.
2).Размеры звеньев: ОА = 20мм, АВ = 76мм, ВС = 26мм, AS2 = 51мм.
План ускорений
м с2
a 0,3
мм
76.
Исследуемаявеличина
aA
aB
n
a BA
Отрезок
на плане
pa a
pa b
an
a BA
nb
a BA
ab
a S2
p a s2
2
Направление
a A // AO
Величина Масштабный Значение
отрезка на коэффициент величины,
плане,
2
мм
a
a B // X X
n
a BA
// AB
a BA
AB
м / c2
0,3
мм
м/c
77.
1.Определение ускорения точки А.Так как угловая скорость
1 является постоянной, то
n
aA aA
aA
2
2
2
1 OA 30 0,02 18 м / c
Вектор ускорения a A направлен параллельно кривошипу ОА от
точки А к точке О.
2
м
/
c
Выбираем масштаб плана ускорений 0,3
a
мм
Найдём отрезок, изображающий вектор ускорения a A
a A 18
на плане:
pa a
60 мм
a 0,3
Из полюса плана ускорений p a откладываем данный отрезок в
направлении, параллельном АО.
78.
2.Определение ускорения точки В.Запишем векторное уравнение: a B a A a BA
Вектор относительного ускорения a BA
раскладываем
нормальную и касательную составляющие:
n
a BA a BA a BA
Нормальное относительное ускорение равно:
n
aBA
22 AB
м с2
Найдём отрезок, изображающий вектор ускорения
на плане:
an
an
BA
a
мм.
n
a BA
на
79.
nПродолжаем строить план ускорений. Вектор ускорения a BA
направлен параллельно АВ. Откладываем отрезок an из точки
плана ускорений в указанном направлении от точки В к точке А.
a
a BA
Вектор ускорения
направлен перпендикулярно АВ. Проводим
это направление из точки
плана ускорений.
Вектор ускорения a B направлен параллельно оси x – x.
Проводим это направление из полюса p a . Две прямые линии,
n
проведённые из точек n и p a в указанных направлениях,
пересекаются в точке . Найдем величины ускорений. Измеряя
b
длины полученных отрезков и умножая их на масштаб a ,
получим:
a p b
B
a
a
a BA nb a
a BA ab a
80.
3.Определение ускорения точкиS2
Воспользуемся следствием из теоремы подобия. Составим
пропорцию:
AB
ab
AS 2 as2
ab AS 2
as 2
AB
,
Данный отрезок откладываем на прямой
Точку
ab от точки a .
s 2 соединяем с полюсом p a .
Величина ускорения:
a S2 pa s 2 a
4.Определение углового ускорения шатуна АВ.
a BA
2
c 2
AB
. Для определения направления 2
a BA
переносим вектор
в точку В шатуна АВ и смотрим как она
движется относительно точки А.
81.
Направление этого движения соответствует 2 .В данном случае угловое ускорение 2 направлено против
часовой стрелки.
Пример 3.4
Кинематический
расчёт
кривошипно-коромыслового
механизма. Определение ускорений точек звеньев для заданного
положения механизма.
Дано:
1).Угловая скорость кривошипа является постоянной и равна
.
1 30с 1
2).Размеры звеньев: О1А = 20 мм, АВ = 50 мм, ВО2 = 30 мм, ВС =
25 мм.
82.
План ускоренийa =
2
м
/
с
0,3
мм
83.
Исследуемаявеличина
aA
aB
a
n
B
Отрезок
на плане
pa a
pa b
pa m
aB
mb
n
a AB
a BA
an
nb
a BA
ab
a S2
p a s2
a S3
р а s3
2
3
Направление
a A // AO
Величина
отрезка на
плане,
мм
Масштабный
коэффициент
Значение
величины,
a
м / c2
n
aB // BO2
aB BO2
n
a AB // AB
a BA
AB
м / c2
0,3
мм
84.
1.Определение ускорения точки А.Так как угловая скорость 1 является постоянной, то
n
aA aA
a A 12 OA 30 2 0,02 18 м / c 2
Вектор ускорения a A направлен параллельно кривошипу О1А от
точки А к точке О1.
Выбираем масштаб плана ускорений
м / c2
a 0,3
мм
Найдём отрезок, изображающий вектор ускорения a A
на плане:
pa a
aA
a
18
60 мм
0,3
Из полюса плана ускорений p a откладываем данный отрезок в
направлении, параллельном О1А.
85.
2. Определение ускорения точки В.Запишем векторное уравнение:
a B a A a BA
Вектор относительного ускорения
.
a BA
раскладываем на нормальную и касательную составляющие:
n
a BA a BA a BA
Нормальное относительное ускорение равно:
a
n
BA
AB
2
2
м с2
Найдём отрезок, изображающий вектор ускорения
на плане:
n
a BA
an
мм
a
n
a BA
86.
na BA
Продолжаем строить план ускорений. Вектор ускорения
направлен параллельно АВ. Откладываем отрезок an из точки
a плана ускорений в указанном направлении от точки В к точке
.
.
А.
Вектор ускорения a BA направлен перпендикулярно АВ. Проводим
это направление из точки n плана ускорений.
Вектор ускорения a
раскладываем на нормальную и
B
n
касательную составляющие:
aB aB aB
Нормальное ускорение равно:
a Bn 32 BO 2 м с 2
Найдём отрезок, изображающий вектор ускорения
на плане:
an
pa m
B
a
мм
n
aB
87.
Найдемвеличины ускорений. Измеряя длины полученных
.
отрезков и умножая их на масштаб a , получим:
a B pa b a
a BA nb a
a BA ab a
a B mb a
3.Определение ускорения точки
aA
aS1
2
S1
88.
S24.Определение ускорения точки
Воспользуемся следствием из теоремы подобия. Составим
,
пропорцию:
AB
ab ,
ab AS 2
as 2
AS 2 as2
AB
Данный отрезок откладываем от точки
a . Точку s 2
соединяем с полюсом p a . Величина ускорения:
a S2 pa s 2 a
5.Определение ускорения точки
.
Воспользуемся следствием из теоремы подобия. Составим
пропорцию:
BS 3 bs3 , bs pa b BS 3
3
BO 2
BO 2
pa b
89.
Данный отрезок откладываем от точки b . Точкусоединяем с полюсом pa . Величина ускорения:
s3
a S3 p a s3 a
6.Определение углового ускорения шатуна АВ.
a BA
2
AB
c 2
переносим вектор a BA
Для определения направления 2
в точку В шатуна АВ и смотрим как она движется относительно
точки А. Направление этого движения соответствует
2 .
В данном случае угловое ускорение
2 направлено против
часовой стрелки.
90.
7 .Определение углового ускорения коромысла ВO2.a B
3
BO 2
c 2
переносим
вектор
Для определения направления 3
aB
в точку В коромысла ВО2 и смотрим как она движется
относительно точки О2. Направление этого движения
соответствует
3 . В данном случае угловое ускорение 3
направлено по часовой стрелке.
91.
ЛЕКЦИЯ 4Краткое содержание
Кинематическое исследование рычажного шестизвенника.
Пример 4.1.
Определение скоростей точек звеньев и угловых скоростей
звеньев для заданного положения механизма.
Дано:
n1 60
1).Число оборотов кривошипа равно
об/мин.Угловая
скорость кривошип а является постоянной.
2).Размеры звеньев:
О1А=150 мм, АВ=200мм, ВС=500мм, ВО2=185 мм, AS1=75 мм,
AS2=100 мм, ВS3=92,5 мм, ВS4 =250 мм.
92.
План скоростейv 0,01
м/с
мм
93.
1. Определение угловой скорости кривошипаn1
.
3,14 60
1
6,28 с-1.
30
30
2. Определение скорости точки А.
VA 1 O1 A 6,28 0,15 0,94 м / с
Вектор скорости V перпендикулярен кривошипу О1А.
A
Выбираем масштаб плана скоростей V 0,01 м / c
мм
Найдём отрезок, изображающий вектор скорости V A
на плане:
V
0,94
pV a
A
V
0,01
94 мм
94.
Из полюса плана скоростейpV
откладываем данный отрезок
в направлении, перпендикулярном О1А в направлении угловой
скорости 1
3. Определение скорости точки В.
Запишем векторное уравнение:
VB V A VBA
Направления векторов скоростей: V BO
B
2 , V BA BA
Продолжим строить план скоростей.
Из конца вектора V проводим направление вектора VBA
A
Из полюса проводим направление вектора V B .
На пересечении двух проведённых направлений получим точку
b .Измеряя длины полученных отрезков и умножая их на
масштаб V, получим значения скоростей:
95.
VB pV b VVBA ab V
4. Определение скорости точки С.
Запишем векторное уравнение:
VC VB VCB
Направления векторов скоростей: VC // X X ,
VCB CB
Продолжим строить план скоростей.
Из конца вектора проводим направление вектора
VB
Из полюса проводим направление вектора
VC
VCB
На пересечении двух проведённых направлений получим точку
c
96.
Измеряя длины полученных отрезков и умножая их на масштабV , получим значения скоростей:
VC pV c V
VCB cb V
5. Определение угловой скорости шатуна АВ.
VBA
2
AB
Для определения направления переносим вектор V
BA
2
в точку В шатуна АВ и смотрим как она движется относительно
точки А. Направление этого движения соответствует
2
В данном случае угловая скорость
стрелке.
2 направлена по часовой
97.
6. Определение угловой скорости коромысла ВО2.VB
3
BO 2
Для определения направления переносим вектор
VB
3
в точку В коромысла ВО2 и смотрим как она движется
относительно точки О2. Направление этого движения
соответствует
. В данном случае угловая скорость
3
3
направлена по часовой стрелке.
7. Определение угловой скорости шатуна ВС.
V
4 CB
BC
Для определения направления переносим вектор V
4
CB
в точку С шатуна СВ и смотрим как она движется относительно
точки В. Направление этого движения соответствует 4 .
В данном случае угловая скорость 4 направлена по часовой
стрелке.
98.
Исследуемаявеличина
VA
VB
VBA
VC
VCB
2
3
4
Отрезок
на плане
pV a
pV b
Направление
V A O1 A
VB BO 2
V BA BA
ab
pV c VC // X X
cb
Величина
Масштабный
отрезка
коэффициент
на плане,
μv
мм
VCB CB
м/с
0,01
мм
Значение
величины,
м/с
99.
Пример 4. 2..Определение
ускорений точек звеньев и угловых ускорений
звеньев для заданного положения механизма.
Решение.
1.Определение ускорения точки А.
Так как угловая скорость является постоянной, то
1
n
aA aA
a A 12 O1 A 6,282 0,15 5,9 м / c 2
Вектор ускорения a A направлен параллельно кривошипу О А
1
от точки А к точке О1.
100.
Выбираем масштаб плана ускоренийм / c2
a 0,05
мм
Найдём отрезок, изображающий вектор ускорения a A
на плане: p a a A 5,9 118 мм . Из полюса плана ускорений
a
a 0,05
p a откладываем данный отрезок в направлении, параллельном
АО1.
101.
2.Определение ускорения точки В.Запишем векторное уравнение:
a B a A a BA
Вектор относительного ускорения a BA раскладываем
нормальную и касательную составляющие:
n
a BA a BA a BA
Нормальное относительное ускорение равно:
n
aBA
22 AB
м с2
n
Найдём отрезок, изображающий вектор ускорения a BA
на плане:
an
n
a BA
a
мм.
на
102.
na
Продолжаем строить план ускорений. Вектор ускорения BA
направлен параллельно АВ. Откладываем отрезок an
из точки a плана ускорений в указанном направлении от точки В
к точке А.
Вектор ускорения направлен перпендикулярно АВ.
a BA
Проводим это направление из точки
План ускорений
n плана ускорений.
м с2
a 0,05
мм
103.
Вектор ускорения a B раскладываем на нормальную икасательную составляющие:
n
aB aB aB
n
Найдём отрезок, изображающий вектор ускорения a B
на плане:
pa m
a Bn
a
мм
n
Продолжаем строить план ускорений. Вектор ускорения a
B
направлен параллельно ВO2. Откладываем отрезок pa m
из точки pa плана ускорений в указанном направлении от точки
перпендикулярно
В к точке O2. Вектор ускорения a B направлен
ВO2. Проводим это направление из точки m плана ускорений. Две
прямые линии, проведённые из точек n и m
в указанных направлениях, пересекаются в точке b .
104.
Найдем величины ускорений. Измеряя длины полученныхотрезков и умножая их на масштаб a , получим:
a B pa b a
a B mb a
a BA nb a
a BA ab a
3.Определение ускорения точки C.
Запишем векторное уравнение:
aC aB aCB
Вектор относительного ускорения
aCB
раскладываем на нормальную и касательную составляющие:
n
aCB aCB aCB
105.
Найдём отрезок, изображающий вектор ускоренияна плане:
bk
n
aCB
a
n
aCB
мм.
Продолжаем строить план ускорений. Так как отрезок
bk
мал, то его на плане ускорений не откладываем. Точки b и k
совпадают.
aCB направлен перпендикулярно ВС.
Вектор ускорения
плана ускорений.
Проводим это направление из точки
k
106.
направлен параллельно оси x – x.aC
Вектор ускорения
Проводим это направление из полюса p a . Две прямые линии,
проведённые из точек k и p a в указанных направлениях,
пересекаются в точке
.
c
Найдем величины ускорений. Измеряя длины полученных
отрезков и умножая их на масштаб , получим:
a
aC pa c a
aCB
kc a
aCB cb a
107.
4.Определение ускорения точки S1.
aS1 12 AS1 6,282 0,075 2,95 м / c 2
Вектор ускорения a S направлен параллельно кривошипу О1 А от
1
точки S1 к точке О1.
S
5.Определение ускорения точки
Воспользуемся следствием из теоремы подобия. Составим
пропорцию:
AB
ab
, as ab AS 2
2
AS 2
as2
2
AB
Данный отрезок откладываем на прямой
Точку s 2 соединяем с полюсом p a .
Величина ускорения:
a S2 pa s 2 a
ab
от точки
a.
108.
Данный отрезок откладываем на прямой pa bТочку s3 соединяем с полюсом
Величина ускорения:
от точки b .
pa .
a S 3 p a s3 a
6.Определение ускорения точки S 4 .
Воспользуемся следствием из теоремы подобия. Составим
пропорцию:
BC
bc
, bs bc BS 4
4
BS 4 bs 4
BC
Данный отрезок откладываем на прямой bc от точки b
Точку
s4
соединяем с полюсом
Величина ускорения:
pa .
aS4 pa s4 a
109.
8.Определение углового ускорения шатуна АВ.a BA
2
AB
c 2
Для определения направления 2 переносим вектор a BA
в точку В шатуна АВ и смотрим как она движется относительно
точки А. Направление этого движения соответствует
2
В данном случае угловое ускорение направлено против
2
часовой стрелки.
9.Определение углового ускорения коромысла ВO2.
a B
3
c 2
BO 2
Для определения направления
3
переносим вектор a
B
в точку В коромысла ВО2 и смотрим как она движется относительно
точки О2. Направление этого движения соответствует 3 . В данном
случае угловое ускорение 3 направлено по часовой стрелке.
110.
10.Определение углового ускорения шатуна ВС.a CB
4
c 2
BC
Для определения направления переносим вектор 4 в точку C
шатуна ВС и смотрим как она движется относительно точки
B.
Направление
этого
движения
соответствует aCB
.
В данном случае угловое ускорение 4 направлено против часовой
стрелки.
111.
Исследуемая величинаОтрезок
плане
на
Направление
Величина
отрезка на плане,
мм
aA
n
a BA
a BA
a BA
pa a
an
nb
n
a BA
// AB
a BA
AB
ab
pa m
n
aB // BO2
aB
mb
aB BO2
aB
pa b
n
CB
a
aCB
aCB
bk
aC
pa c
a S1
a
a A // AO1
n
B
a
Масштабный
коэффициент
ck
bc
pa s1
n
aCB // CB
aCB
CB
aC // X X
a S1 // AO1
м / c2
0,05
мм
Значение величины,
2
м/c
112.
a S2p a s2
a S3
p a s3
a S4
pa s4
2
3
4
113.
ЛЕКЦИЯ 5Краткое содержание
• Силовой анализ механизмов.
• Основные задачи.
• Силы, действующие на звенья механизма.
• Реакции в кинематических парах.
• Принципы и последовательность силового расчёта.
• Типовые расчёты групп Ассура .
114.
Задачи силового анализаОсновными задачами силового анализа являются:
1.Определение реакций в кинематических парах. Знание этих
реакций позволяет путём проведения расчетов на прочность и
жесткость выбрать оптимальные размеры и форму звеньев
механизма.
2.Определение уравновешивающих сил Fур или моментов сил
M ур , которые нужно приложить к ведущим звеньям для
удержания механизма в заданном положении либо для обеспечения
требуемого движения ведущих звеньев. При этом считаются
известными массы всех звеньев, все внешние силы и моменты,
действующие на звенья, а также законы движения звеньев.
115.
1.Движущие силы и моменты движущих силК движущим силам Fд или моментам движущих сил M д
относят такие, которые обеспечивают движение механизма.
Векторы движущих сил или совпадают с векторами скоростей тех
точек звеньев механизмов, к которым они приложены, или
составляют острые углы. Моменты движущих сил направлены в
сторону угловой скорости звена (рис.5.1). С энергетической точки
зрения работа движущих сил и моментов движущих сил Ад
положительна.
2.Силы сопротивления и моменты сил сопротивления
на
Силы сопротивления Fc или моменты этих сил M c делятся
силы F и моменты M п.с. полезных
или
технологических
n.c.
сопротивлений и силы F и моменты М в .с. вредных
в .с .
сопротивлений.
2.1.Силами полезных сопротивлений Fn.c. или моментами этих
сил M п.с. называют такие, для преодоления которых создана
машина. С энергетической точки зрения работа сил полезных
сопротивлений Ап.с. отрицательна.
116.
2.2.К силам вредных сопротивлений Fв.с. относят силы трения вкинематических парах, силы аэродинамических сопротивлений и
др. На преодоление этих сил затрачивается дополнительная работа
сверх той, которая необходима для определения полезного
сопротивления. Поэтому работа сил суммарных
сопротивлений
Ас Ап.с Ав.с. . Векторы сил Fc
направлены
в
противоположную сторону векторов скоростей тех точек звеньев
механизма, к которым они приложены, или составляют с ними
тупые углы, а моменты сил сопротивления M c направлены
противоположно вращению звена. (рис.5.1).
Деление сил на движущие и силы сопротивления имеет некоторую
условность. Так силы тяжести звеньев при подъёме их центров масс
оказывается силами сопротивлений, а при опускании центров –
силами движущими; силы трения между шкивом и ремнём в
ременной передаче являются движущими.
117.
Примеры сил. У двигателя внутреннего сгорания движущейсилой Fд является давление расширяющегося газа на поршень.
Силами сопротивления будут: сила трения в подшипниках и
цилиндрах, сопротивление воздуха, сопротивление рабочей
машины, которая приводится в движение двигателем, и т.п.
а)
Fc
б)
Fд
V
Mc
Mд
ω
Рис.5.1
118.
3.Силы инерцииFи и моменты сил инерции
Mи
Возникают при движении звеньев. В быстроходных механизмах
по величине эти силы могут превосходить другие силы. Силы
инерции, действующие на каждое звено механизма, приводятся к
главному вектору и главному моменту инерционных сил:
Fи ma s
M и I s
(5.1)
(5.2)
где m – масса звена;
a s - ускорение центра массы звена;
ε - угловое ускорение звена;
I s – момент инерции масс звена относительно оси,
проходящей через центр масс и перпендикулярной плоскости
движения звена.
119.
Направление этих сил и моментов обратно направлениямсоответствующих ускорений, а их работа за время рабочего цикла
равна нулю (рис. 5.2).
Рис.5.2
120.
4.Силы тяжести (веса) звеньевПрикладываются в центре масс звена направлены вертикально
вниз. Вычисляются по формуле:
(5.3)
где m – масса звена;
g 9,81
G m g,
- ускорение свободного падения.
Реакции в кинематических парах
Реакция Rij – это усилие, с которым одно звено i воздействует
на другое
звено j в местах их соприкосновения или наоборот. При
этом Rij R ji .
Реакция в кинематической паре характеризуется величиной,
направлением и точкой приложения.
м с2
121.
1.Реакция во вращательной кинематической паре (рис. 5.3)Известна точка приложения реакции и неизвестны направление и
Rij раскладывают
на
числовое значение
n реакции. Реакцию
нормальную Rij и касательную Rij составляющие. При этом
составляющая R n направлена вдоль звена, составляющая Rij
ij
– перпендикулярно к звену.
Рис. 5.3
122.
2.Реакция в поступательной кинематической паре (рис.5.4)., неизвестны её
Известно направление реакции
( Rij x x)
числовое значение и точка приложения.
Рис.5.4
123.
3.Реакция в высшей кинематической паре (рис. 5.5).В высшей кинематической паре плоского механизма известны
точка приложения реакции и её направление (вдоль нормали n-n), но
неизвестно числовое значение реакции
Рис.5.5
124.
Принципы и последовательность силового расчетаПри силовом расчете механизма в число известных внешних сил,
приложенных к его звеньям, входит инерционная нагрузка на
звенья. Такой силовой расчет механизма называется
кинетостатическим.
При этом используется следующие принципы:
1.Принцип Даламбера:
В применении к механизмам, сущность принципа заключается в
следующем:
если ко всем внешним нагрузкам, действующим на звено
механизма, присоединить
силы инерции и моменты инерции, то под действием всех этих
нагрузок звено можно рассматривать условно находящимся в
равновесии.
2.Принцип освобождаемости от связей:
не нарушая движения или покоя системы, можно
отбрасывать отдельные связи и прикладывать к системе
соответствующие этим связям реакции.
125.
3.Группа Ассура является статически определимойкинематической цепью.
Для каждого подвижного звена группы Ассура можно написать
три уравнения равновесия; для n звеньев число уравнений
равновесия будет 3n.
Реакция каждой низшей одноподвижной кинематической пары
содержит
два
неизвестных.
Следовательно,
условие
кинетостатической определимости имеет вид 3n-2p1=0.
Это совпадает с условиями, которым удовлетворяют структурные
группы Ассура. Следовательно, группы Ассура являются статически
определимыми системами. Поэтому кинетостатический расчет
ведут для отдельных групп Ассура механизма, начиная с последней
(наиболее удаленной от начального механизма).
126.
Порядок кинетостатического расчета механизма1.Отсоединить последнюю группу Ассура от механизма и
приложить к ней известные силы, в том числе силы и моменты
инерции, а действие отброшенных звеньев заменить реакциями.
2.Определить значение касательной составляющей реакции во
внешней вращательной кинематической паре. Для этого записать
сумму моментов всех сил, действующих на одно звено группы
Асcура, относительно внутренней кинематической пары.
n
M 0 ( Fi ) M 0 ( Rij ) 0
n
i 1
i 1
Из уравнения найти искомую реакцию.
(5.3)
127.
3.Определить значение нормальной составляющей реакции вовнешней поступательной кинематической паре. Для этого записать
векторное уравнение равновесия всех сил, действующих на всю
n
n
группу Ассура.
F i Rij 0
(5.4)
i 1
i 1
Данное уравнение решается графически путем построения
плана сил.
4.Отсоеденить предпоследнюю группу Ассура механизма и
выполнить аналогичные расчеты и так до тех пор пока не останется
начальный механизм.
5.Провести расчет начального механизма.
128.
Силовой расчет рычажного шестизвенникаСиловой расчет группы Аcсура вида ВВП
129.
Дано:Массы звеньев: m4=2 кг, m5 = 5 кг.
Момент инерции относительно оси, проходящей через центр масс
звена 4:
I S 4 0,05 кгм2.
Ускорения центров масс звеньев:
a C = 3,35 м/с2,
a S 4 = 3,5 м/с2.
Угловое ускорение звена 4:
4 = 9,5 с-2.
Длина звена ВС = 500 мм. Движущая сила F= 30 н.
130.
1).Определение сил тяжести звеньев:= 2 9,8 20
н,
G5 m5 g = 5 9,8 50
н.
G4 m4 g
2).Определение сил инерции:
Fи m5 aC = 5 3,35 16,75 н.
Fи m4 a S = 2 3,5 7 н,
4
4
5
Силы инерции направлены в противоположную
соответствующим ускорениям центров масс звеньев.
сторону
131.
3).Определение момента инерции:M и4 I S 4 4 =
0,05 9,5 0,475
нм;
Момент инерции направлен в противоположную
сторону
;
угловому ускорению έ4.
Построим группу Ассура в масштабе 1:5.
Покажем все действующие на нее силы и неизвестные реакции
R65, R 34, Rn34, R54.
1.Определим реакцию R .
34
Составим уравнение моментов всех сил, действующих на звено 4, относительно точки С.
n
M 0
i 1
C
132.
Найдем реакцию R 34.Длины плеч h и h измерены на расчетной схеме и умножены на
1
2
масштаб.
2.Определим реакции Rn и R .
34
65
Составим векторное уравнение равновесия всех сил, действующих на всю группу Ассура.
Fi 0
n
н
мм
i 1
Выберем масштаб плана сил F= 0,5
Вычислим величины отрезков, соответствующих векторам сил.
Данные занесем в таблицу 1.
133.
Обозначениесилы
G4 G
5
Величина
силы, н
Отрезок на
плане, мм
Fи4 Fи
F
5
n
R34
R34
R34 R54
134.
Строим план сил. В соответствии с векторнымуравнением
откладываем отрезки, соответствующие векторам G4 , G5 , Fè 4 , Fè 5 , F , R34
R34
Начать построение необходимо с вектора
. Далее строим
векторы в любом порядке.
Затем
из
начала
вектора
R
34 проводим
п
направление вектора R34 , а из конца последнего вектора проводим
.
направление вектора R65
Пересекаясь, эти направления замыкают многоугольник сил.
на плане сил отрезки, соответствующие векторам
,
п Измеряя
R
34
,
R34 R65 и умножая их на масштаб F, получим значение этих
реакций. Данные занесены в таблицу 1.
135.
3.Определим реакцию R54.Составим векторное уравнение равновесия всех сил,
n
действующих звено 4.
F 0
i 1
i
н
Выберем масштаб плана сил F=0,5 мм .
Строим план сил. В . соответствии с векторным уравнением
откладываем отрезки, соответствующие векторам
G4 , Fи 4 , R 34 .
Векторы можно откладывать в любом порядке. Соединяя начало
первого вектора и конец последнего, получим многоугольник сил и
отрезок, определяющий реакцию R54 . Измеряя его длину и
R
умножая на масштаб F, получим величину реакции 54. Реакция
R54 R45
136.
4.Определим место расположения реакции R65.Составим уравнение моментов всех сил, действующих на звено 5,
относительно точки С.
n
M 0
i 1
C
Найдем расстояние х.
Силовой расчет группы Ассура вида ВВВ.
Дано:
Массы звеньев: m2=3 кг, m3 = 3 кг.
Моменты инерции относительно оси, проходящей через центр
масс звеньев 2 и 3:
I S 2 0,05 кгм2,
I S3 0,06 кгм2 .
137.
Ускорения центров масс звеньев 2 и 3:a S 2=4,5 м/с2,
a S 3 =2,45 м/с .
Угловое ускорение звенев 2 и 3
2
2 = 4,5 с
3 = 8,1 с .
-2,
-2
Длины звеньев АВ = 200 мм, ВО2 = 185 мм.
1).Определение сил тяжести звеньев:
G2 m2 g = 3 9,8 30 н,
G3 m3 g = 3 9,8 30 н.
2).Определение сил инерции:
Fи2 m2 a S2
=
Fи3 m3 a S3
=
3 5,45 16,35 н,
3 2,45 7,35 н.
138.
Группа Ассура вида ВВП (масштаб 1:5)F 0,5
н
мм
139.
Силы инерции направлены в противоположную сторонусоответствующим ускорениям центров масс звеньев.
3).Определение моментов инерции:
M и2 I S 2 2
=
0,05 4,5 0,225 нм;
0,06 8,1 0,486 нм.
Моменты инерции направлены в противоположные стороны
соответствующим угловым ускорениям.
Построим группу Ассура в масштабе 1:3.
Покажем все действующие на нее силы (в том числе реакцию
R43 R34) и неизвестные реакции R 12, Rn12, R 36, Rn36.
M и3 I S 3 3
=
140.
1.Определим реакцию R 12.Составим уравнение моментов всех сил, действующих на звено 2, относительно точки В.
n
M 0 ;
i 1
B
Найдем реакцию R 12
2.Определим реакцию R .
63
Составим уравнение моментов всех сил, действующих на звено 3, относительно точки В.
n
M 0
i 1
B
;
Найдем реакцию R 63.
Длины плеч h , h , h и h измерены на расчетной схемы и умножены
1 2 3
4
на масштаб.
141.
3.Определим реакции Rn12 и Rn63.Составим векторное уравнение равновесия всех сил,
.
действующих на всю группу Ассура.
Fi 0
n
i 1
н
мм
Выберем масштаб плана сил F=0,5
142.
Вычислим величины отрезков, соответствующих векторам сил.Данные занесем в таблицу 2.
Строим план сил. В соответствии с векторным уравнением
откладываем отрезки, соответствующие векторам G ,G ,F , F , R , R , R .
2
3
и2
и3
12
63
43
R12 .Остальные векторы
Начать построение необходимо с вектора
можно откладывать в любом
порядке, но обязательно
закончить
R12 проводим
построение вектором R 63. Затем из начала вектора
n
R
R
12
проводим
направление вектора , а из конца вектора
63
n
направление вектора R63 . Пересекаясь, эти направления замыкают
многоугольник
сил.
Измеряя
плане
сил
отрезки,
n n на
соответствующие векторам R12,R63,R12, R63 , и умножая их на
масштаб F, получим значение этих реакций. Данные занесены в
таблицу 2.
143.
Обозначениесилы
Величина
силы, н
Отрезок на
плане, мм
G2
G3 Fи
2
Fи3
R43
R12 R12 R12n
R63
R63
n
R63
144.
Группа Ассура ВВВ (масштаб 1:3)План сил для группы Ассура
F 0,5
н
мм
145.
ЛЕКЦИЯ 6Краткое содержание
1.Силовой расчет начального механизма.
2.Определение уравновешивающей силы и
уравновешивающего момента.
3.Теорема Н.Е. Жуковского о жестком рычаге.
146.
Силовой расчет начального механизмаНачальный механизм состоит из ведущего звена, которое входит
во вращательную или поступательную кинематическую пару со
стойкой.
Кинематическая цепь будет статически определима при условии
3n 2 p1 0
Начальный механизм при n = 1 и p1 = 1 не будет находиться в
равновесии. Для того, чтобы начальный механизм находился в
равновесии, необходимо дополнительно ввести уравновешивающую
силу
или уравновешивающий момент
F ур
M ур , которые бы
уравновесили все силы и моменты, приложенные к ведущему
звену.
147.
Уравновешивающая сила или уравновешивающий моментявляются такой силой или моментом, которые должны быть
приложены к ведущему звену, чтобы механизм двигался по
заданному закону или удерживался в заданном положении.
Что действует на ведущее звено или - зависит от способа
передачи энергии от электродвигателя к валу кривошипа. Возможны
следующие случаи.
• Коленчатый вал двигателя соединяется с валом рабочей машины
муфтой (рис.6.1). В этом случае к валу приложен
уравновешивающий момент.
Электродвигатель.
рис. 6.1.
148.
Пример 6.1Дано:
Масса звена: m1=2 кг.
Ускорения центра масс звена: a = 2,95 м/с2,.
S1
1).Определение силы тяжести звена:
G1 m1 g = 2 9,8 20 н
.
2).Определение силы инерции:
Fи1 m1 a S1 = 2 2,95 5,9 н.
Сила инерции направлена в противоположную сторону
ускорению a S .
1
Построим начальный механизм в масштабе 1:5.
Покажем все действующие на него силы, неизвестную реакцию
R61 и уравновешивающий момент
M ур
149.
1.Найдем величину уравновешивающего моментаM ур
Запишем уравнение моментов всех сил относительно точки О1.
M O1 ( Fi ) 0
n
i 1
План сил для начального механизма
F 0,5
н
мм
150.
Уравновешивающий момент M ур равен:Здесь
R21 R12
Длины плеч h1 и h2 измерены на расчетной схеме и умножены на
масштаб.
2.Найдем реакцию R61.
Составим векторное уравнение равновесия всех сил,
действующих на начальный механизм.
н
Fi 0 мм
n
i 1
Выберем масштаб плана сил F= 0,5
Вычислим величины отрезков, соответствующих векторам сил.
Данные занесем в таблицу 1:
151.
Таблица 1Обозначен
ие
силы
Величина
силы, н
Отрезок
на
плане, мм
G1
Fи1
R21
R61
152.
Строим план сил. В соответствии с векторным уравнением, ,
откладываем отрезки, соответствующие
векторам G
,
R
F
1
и1
21
Векторы можно откладывать в любом порядке. Соединяя начало
первого вектора и конец последнего, получим многоугольник сил и
отрезок, определяющий реакцию R61 .
Измеряя его длину и умножая на масштаб F, получим величину
реакции R61 . Данные занесены в таблицу 1.
2.Вал двигателя соединяется с валом рабочей машины при
помощи зубчатой передачи (рис.6.2). В этом случае к валу двигателя
приложена уравновешивающая сила, которая действует по линии
зацепления.
153.
ЭлектродвигательЗубчатый
механизм
Рис. 6.2
154.
Пример 6.2.Дано:
Масса звена: m1=2 кг. Ускорения центра масс звена:
a S1 = 2,95 м/с2.
1).Определение силы тяжести звена:
G1 m1 g = 2 9,8 20 н
.
2).Определение силы инерции:
Fи1 m1 a S1 = 2 2,95 5,9 н.
155.
Сила инерции направлена в противоположную сторону ускорениюa S1 . Построим начальный механизм в масштабе 1:5.
Покажем все действующие на него силы, неизвестную реакцию
R61 и уравновешивающую силу Fур, которую приложим
перпендикулярно кривошипу АО1 в точке А.
План сил для начального механизма
F 0,5
н
мм
156.
1.Найдем величину уравновешивающей силы Fур.Запишем уравнение моментов всех сил относительно точки О1.
M O1 ( Fi ) 0
n
.
i 1
Уравновешивающая сила Fур равна:
Здесь
R21 R12
Длины плеч h1 и h2 измерены на расчетной схеме и умножены на
масштаб.
2.Найдем реакцию R61.
Составим векторное уравнение равновесия всех сил,
действующих на начальный механизм.
Fi 0
n
i 1
157.
Выберем масштаб плана сил F=0,5н
мм
Вычислим величины отрезков, соответствующих векторам сил.
Данные занесем в таблицу 2:
Обозначе
ние
силы
G1
Fи1
R21
Величина
силы, н
Отрезок
на
плане, мм
Таблица 2
Fур
R61
158.
Строим план сил. В соответствии с векторным уравнениемоткладываем отрезки, соответствующие векторам G1 , Fи ,R21 ,Fур
Векторы можно откладывать в любом порядке. Соединяя начало
первого вектора и конец последнего, получим многоугольник сил и
отрезок, определяющий реакцию R61 .
1
Измеряя его длину и умножая на масштаб F, получим величину
реакции R . Данные занесены в таблицу 2.
61
159.
Теорема о жестком рычаге Н.Е. ЖуковскогоН.Е.Жуковский показал, что равновесию механизма с одной
степенью свободы соответствует равновесие некоторого рычага, и
предложил способ построения и нагружения такого рычага.
Теорему Н.Е.Жуковского можно сформулировать так:
Если векторы всех сил, приложенных к различным точкам
звеньев и уравновешенных на механизме, перенести параллельно
самим себе в одноимённые точки повёрнутого на 90 плана
скоростей, приняв фигуру плана за жесткий рычаг, то сумма
моментов всех указанных сил относительно полюса плана будет
равна нулю.
160.
Пример 6.3.Для
кривошипно-ползунного
уравновешивающую силу Fyp .
механизма
определить
Решение.
1.Уравновешивающую силу Fyp приложим
в
точке
А
перпендикулярно кривошипу АО. Построим план скоростей и
повернем его на 90 . В соответствующих точках плана скоростей
приложим векторы сил, сохраняя их направления, момент M
2
Mи
заменим парой сил F2
и каждую силу перенесем на план.
2
AB
2.Составим уравнение моментов всех сил относительно полюса
pV :
M pV ( Fi ) 0
n
i 1
Решая уравнение, получим:
Длины всех плеч измерены на расчетной схеме .
161.
План скоростей, повернутый на 90○План скоростей
162.
Таким образом, с помощью теоремы Жуковскогоможно:
1.Определить уравновешивающую силу F ,не
проводя
yp
силового расчета;
2.Проверить значение уравновешивающей силы Fyp , полученной
из силового расчета. Погрешность расчетов составляет
Fур Fур
Fур
100 %. Погрешность не должна превышать 20 %.
163.
ЛЕКЦИЯ 7Краткое содержание
1.Задача об уравновешивании механизма.
2.Уравновешивание машин на фундаменте.
3.Уравновешивание вращающихся масс (роторов).
4.Условия статического и динамического уравновешивания
роторов.
5.Статическая и динамическая балансировка механизмов.
164.
При движении звеньев механизма в кинематических парахвозникают дополнительные динамические нагрузки от сил инерции
звеньев. Так как всякий механизм имеет неподвижное звено- стойку,
то и стойка механизма также испытывает динамические нагрузки. В
свою очередь через стойку эти нагрузки передаются на фундамент
механизма.
Динамические нагрузки, возникающие при движении, являются
источниками вибраций и колебаний в звеньях и фундаменте,
дополнительных напряжений в звеньях, причиной шума и т. д.
Поэтому при проектировании механизма ставится задача об
устранении такого вредного воздействия, полном или частичном
гашении указанных динамических нагрузок. Эта задача носит
название задачи об уравновешивании механизма.
165.
Уравновешивание машин на фундаментеУравновешенность является свойством или характеристикой
механизма и не должна зависеть от действующих на него внешних
сил. Если исключить из рассмотрения все внешние силы, то
останутся только инерционные нагрузки, которые определяются
инерционными параметрами механизма - массами и моментами
инерции, а также законом движения (например, центра масс
системы).
166.
Уравновешенным считается механизм, в котором главныевекторы сил инерции и моментов сил инерции равны нулю:
Fè 0
Ì è 0
(7.1)
(7.2)
В практике машиностроения при уравновешивании механизмов
указанные условия выполняются только частично, в зависимости от
конкретно поставленной задачи.
Специальные мероприятия, выполняемые при проектировании
механизма и ставящие своей целью достичь условия (7.1)
представляют собой статическое
уравновешивание механизма.
Поскольку Fи ma s , то условие (7.1) выполняется только при
as =0, что в свою очередь, возможно лишь в том случае, когда
центр масс S системы подвижных звеньев механизма не
перемещается.
167.
Таким образом, статическое уравновешивание есть такоедействие, в результате которого центр масс системы подвижных
звеньев работающего механизма становится неподвижным. Достичь
этого можно различными способами.
1.Рассмотрим метод заменяющих масс.
Уравновесим силы инерции шарнирного четырехзвенника.
Рис.7.1
168.
Разместим противовесы (корректирующие массы) на подвижныхзвеньях.
1.На продолжении (вниз) звена ОА на некотором расстоянии l1 от
точки О устанавливаем противовес массой mпр1 таким образом,
чтобы центр масс звена 1 вместе с противовесом совпал с
неподвижной точкой О. Для этого должно быть соблюдено
равенство:
Задаваясь из конструктивных соображений расстоянием l1,
определим массу противовеса mпр1
2.На продолжении звена АВ (вправо) на некотором расстоянии l2
от точки В устанавливаем противовес массой mпр2 таким образом,
чтобы центр масс звена 2 вместе с противовесом совпал с точкой В.
Для этого должно быть соблюдено равенство:
Задаваясь из конструктивных соображений расстоянием l2,
определяем массу противовеса mпр2
169.
3.На продолжении звена ВС (вниз) на некотором расстоянии l3 отточки С устанавливаем противовес массой mпр3 таким образом,
чтобы центр масс звеньев 2 и 3 вместе с противовесами совпал с
точкой С. Для этого должно быть соблюдено равенство:
Задаваясь из конструктивных соображений величиной l3,
определяем массу противовеса mпр3
Таким образом, центр масс звена 1 со своим противовесом
совпадает с неподвижной точкой О, центр масс звеньев 2 и 3 вместе
с их противовесами совпадает с неподвижной точкой С.
Следовательно, центр всех масс будет также совпадать с
неподвижной точкой, и результирующая сил инерции будет равна
нулю.
170.
Необходимо отметить, что при уравновешивании данным методомуравновешиваются только силы инерции звеньев. Моменты сил
инерции не уравновешиваются, т.е. условие (7.2) не выполняется,
такой механизм является моментно не уравновешенным.
2.Рассмотрим
уравновешивание
механизмов
методом
рационального размещения звеньев.
Схемы шарнирного четырехзвенного и кривошипно-ползунного
механизмов изображены на рис.7.2 и рис.7.3. Как видно, в этих
механизмах к ведущему звену 1 симметрично присоединены по две
одинаковые группы Ассура (2, 3) и (2 , 3 ), благодаря чему силы
инерции соответствующих симметрично расположенных звеньев
равны по величине, но обратные по направлению, т. е. попарно
уравновешиваются.
171.
Рис.7.2Рис. 7.3
172.
Конечно, такое размещение звеньев механизма очень громоздко ине всегда целесообразно. Зачем, например, ставить дополнительную
группу Ассура только для уравновешивания машины, если для ее
работы достаточна только одна группа Ассура. Поэтому такое
уравновешивание на практике применяется редко. Оно
целесообразно, но только в случаях, когда в машине работают оба
симметричных механизма (обе группы Ассура), например в
многоцилиндровых двигателях внутреннего сгорания и др.
Уравновешивание вращающихся масс (роторов)
Ротором называют любое вращающееся тело.
Роторами являются валы быстроходных двигателей, центрифуги,
турбины, шпиндели токарных станков и т.д., скорость вращения
которых достигает 20000-50000 об/мин.
Рассмотрим вал, вращающийся в подшипниках A с постоянной
угловой скоростью ω. С валом жестко связаны заданные массы m1,
m2 и m3 (рис. 7.4), расположение в трех плоскостях Т1, Т2, Т3,
перпендикулярных к оси вращения z-z на расстояниях r1,r2 и r3.
173.
Рис.7.4174.
Силы инерции, развиваемые этими массами равны:Fи m as m r1 , Fи 2 m as2 m r2 ,
1
1
2
2
1
2
1
2
Fи m as m r3 .
3
3
2
3
3
Результирующая сила инерции всего тела или главный вектор сил
инерции равен:
n
Fи m ri m rs
2
i 1
2
i
,
где m - масса всего тела,
rs - расстояние от центра масс всего тела до оси вращения;
m rS - статический момент.
175.
Результирующий момент всех сил инерции или главный моментсил инерции равен:
M и m ri l I
где
2
i 1
n
m ri l I r
i
i 1
n
2
i
i
r
– центробежный момент инерции относительно
i
оси вращения.
Главный вектор сил инерции Fи и главный момент сил инерции
M и оказывают дополнительное динамическое давление на опоры
(подшипники), вызывающее вибрации стойки.
Устранение этого вредного воздействия называют
уравновешиваем роторов.
Условиями полного уравновешивания являются
n
Fи 0 , m r m rs 0
i 1
i
n
Mи 0,
i
m ri l I r 0
i 1
i
(7.3)
i
(7.4).
176.
Условие(7.3)
называется
условием
статической
уравновешенности и будет выполнено при rs=0, то есть когда центр
S масс ротора лежит на оси вращения.
Мерой статической неуравновешенности ротора служит величина
статического дисбаланса
Dст m rS .
Для устранения статической неуравновешенности ротора
необходимо в произвольной плоскости на любом расстоянии от оси
вращения расположить одну дополнительную массу (например, в
плоскости Т0 на расстоянии r0).
Условие
(7.4)
называется
условием
динамической
уравновешенности и будет выполнено только в том случае, когда
ось вращения совпадает с одной из главных осей инерции ротора.
177.
Мерой динамической неуравновешенности служит величинадинамического дисбаланса ротора
Dд m ri l
n
.
Для устранения динамической неуравновешенности ротора
необходимо в двух произвольных плоскостях на любом расстоянии
от оси вращения расположить две дополнительные массы
(например, в плоскостях Т0 и Т на расстоянии r0 и r).
Следовательно, полное уравновешивание ротора может быть
достигнуто установкой двух дополнительных масс (противовесов),
центры масс которых лежат в двух произвольно выбранных
плоскостях.
i 1
i
i
178.
Рассмотрим пример полного уравновешивания ротора.Пример 7.1
Дано:
К валу, вращающемуся в подшипниках с постоянной угловой
скоростью, закреплены массы.
m2=2кг, m3=3кг, m4=2кг, r2=10мм, r3=15мм , r4=12мм, l1=0,
l2=100мм, l3=200мм, l4=300мм, l5=400мм, 2 30 , 3 210 , 4 270
.
Произвести полное уравновешивание данного ротора.
Решение
Расположим дополнительную массу m1 слева от массы m2 на
расстоянии l=100мм, а m5 - справа от массы m4 на расстоянии
l=100м.
179.
1.Условие динамического уравновешивания (7.4):Найдем динамические дисбалансы. Выбираем масштаб μ=
, делим величины динамических дисбалансов на данный масштаб и
находим соответствующие отрезки. Все значения занесем в таблицу.
Построим план динамических дисбалансов. На плане измеряем
отрезок m5 r5 l5 , вписываем его длину в таблицу. Умножаем
величину данного отрезка на масштаб, т.е. находим динамический
дисбаланс, задаем массу m5 =
кг и находим r5=
Угол ά5 измеряем на построенном плане.
2.Условие статического уравновешивания (7.5)
Найдем статические дисбалансы. Выбираем масштаб μ=
, делим величины статических дисбалансов на данный масштаб и
находим соответствующие отрезки. Все значения занесем в таблицу.
Построим план статических дисбалансов. На плане измеряем
отрезок m1 r1 , вписываем его длину в таблицу. Умножаем величину
данного отрезка на масштаб, т.е. находим статический дисбаланс,
=
кг и находим r1=
задаем массу m1
Угол ά1 измеряем на построенном плане.
180.
Массаmi, кг
Радиус
ri, см
Расстояние до начала отсчета
li, см
i, град
Статический дисбаланс
miri, кгсм
Отрезки для построения плана
статических дисбалансов, мм
Динамический дисбаланс
mirili, кгсм2
Отрезки для построения плана
динамических дисбалансов, мм
1
2
3
4
5
181.
План динамических дисбалансов182.
Балансировка роторовПравильно спроектированный с точки зрения полного
уравновешивания ротор все же может иметь некоторую
неуравновешенность вследствие неоднородности материала,
неточности обработки и сборки, перепадов температур и т. д.
Поэтому все роторы проверяют на специальных балансировочных
машинах.
Статистическая балансировка
При статистической балансировке звено располагается на опорах
и может свободно поворачиваться вокруг своей оси рис. (7.5).Звено
будет поворачиваться до тех пор, пока центр масс звена не займет
нижнее положение. Далее балансирный грузик (пластилин,
мастику) устанавливают на линии ОS0 выше оси вращения. В
результате ряда попыток можно установить, какую массу должен
иметь балансир, чтобы звено занимало безразличное положение (не
перекатывалось).
183.
Далее балансирный груз (противовес) взвешивают, определяютместо его крепления. Часто вместо установки противовесов удаляют
часть металла (высверливают отверстия и др.).
Рис.7.5
Точность статистической балансировки зависит от трения в
опорах. На практике для статистической балансировки используют
приборы, позволяющие сразу определить массу необходимого
балансирного груза и место его установки.
Статистической балансировке подвергают вращающиеся детали
дисковой формы, у которых диаметр больше толщины.
184.
Динамическая балансировкаДинамическая балансировка производится на станках различной
конструкции.
На рис.7.6 приведена схема станка люлечного типа. Ротор 1
устанавливается в подшипниках на люльку 2, шарнирно
прикрепленную к стойке 3. Люлька притягивается к стойке с
помощью пружин 4. Уравновешивания производится в двух
плоскостях - и - , которые выбирают из конструктивных
соображений. В начале балансировки одна из плоскостей ( - )
должна обязательно лежать на оси, проходящей через центр
шарнира люльки.
185.
Рис.7.6186.
При равномерном вращении неуравновешенные массы m1 и m2вызовут появление сил инерции, которые создадут момент
относительно шарнира, и люлька вместе с ротором начнет
колебаться. Эти колебания будут гармоническими и амплитуда их
будет пропорциональна неуравновешенной массе m2.
Колебания фиксируются электрическими датчиками. Токи,
возникающие в них, усиливаются и поступают в специальные
электрические счетные устройства. Результаты вычислений
передаются на специальные приборы, по показаниям которых
определяют значение и положение неуравновешенной массы m2.
Для определения величины и положения другой
неуравновешенной массы m1 переставляют на люльке 2 так, чтобы
плоскость - проходила через шарнир, на котором колеблется
люлька. В таком случае колебания люльки будут вызываться только
силой инерции массы m1, и по амплитуде колебаний можно
произвести уравновешивание.
187.
ЛЕКЦИЯ 8Краткое содержание
1. Зубчатые механизмы.
2. Классификация зубчатых механизмов.
3. Теоремы, определяющие кинематику высших кинематических пар.
Эвольвента окружности и её свойства.
4. Геометрические характеристики эвольвентного зубчатого
колеса.
188.
Зубчатые механизмыЗубчатыми называют механизмы, в которых движение между
звеньями (зубчатыми колесами) передаётся с помощью
последовательного зацепления зубьев.
Зубчатые механизмы имеют высокие технико-экономические
показатели:
• большую долговечность и надежность работы;
• высокий коэффициент полезного действия (до 0,97…0,98 для
одной пары колес);
• простоту технического обслуживания;
• компактность (малые размеры и массу).
Основными недостатками являются:
• высокая трудоёмкость изготовления зубчатых колёс;
• возможность появления шума в процессе работы;
• невозможность бесступенчатого изменения передаточного
отношения в процессе работы.
189.
Классификация зубчатых механизмовПо взаимному расположению осей
• цилиндрические (имеют параллельные оси) рис.8.1, а;
• конические (оси пересекаются) рис. 8.1, б;
• гиперболоидные, червячные и винтовые (оси скрещиваются) рис.
8.1, в.
По относительному расположению поверхностей вершин и
впадин зубьев колёс
• передачи внешнего зацепления (рис.8.1, а, б, в);
• передачи внутреннего зацепления (рис. 8.1 ,г).
190.
По характеру движения осей• обычные передачи - имеют неподвижные геометрические оси
всех колёс;
• планетарные передачи - оси одного или нескольких колёс
подвижны.
По направлению зубьев
• прямозубые (рис. 8.1, а, б);
• косозубые (рис. 8.1, д).
По профилю зубьев
• с эвольвентным зацеплением - профили зубьев очерчены по
эвольвенте;
• с циклоидным зацеплением - профили зубьев очерчены по дугам
эпи- и гипоциклоид;
• с зацеплением Новикова - профили зубьев очерчены по
окружностям.
191.
а).б).
Рис.8.1
в).
192.
г).д).
Рис.8.1
193.
Теоремы, определяющие кинематику высших кинематическихпар
Высшей кинематической парой в зубчатом механизме является
кинематическая пара «зуб - зуб».
1.Теорема о проекциях линейных скоростей точки касания в
высших кинематических парах на общую нормаль
Проекции линейных скоростей точек касания в высшей
кинематической паре на общую нормаль должны быть равны
между собой
n n
V1 V2
Проекции этих же скоростей на общую касательную могут
отличаться как угодно
V1 V2
194.
Следствие теоремыКонцы векторов линейных скоростей точки касания должны
лежать на одном перпендикуляре к общей нормали.
В случае, если n n
V1 V2 , то о дно звено опережает другое
(нарушается контакт), либо одно звено врезается в другое.
2.Основная теорема зацепления
Проведем через точку касания С общие касательную - и
нормаль n-n. Покажем векторы скоростей точки касания С. При
этом: V1 O1C , V2 O2C .
V1 w1 1 , V2 w2 2 ,
где
O1C 1 ,
(8.1)
O2C 2 .
Разложим векторы V 1 и V 2 , на составляющие: нормальные и
касательные,
n
n
V
V
cos
1
Из построений следует, что
V 2 V2 cos 2
1
1 ;
195.
Восстановим из точек О1 и О2 , перпендикуляры на нормальО1 К и
О2 L , которые равны:
(8.3)
Подставим (8.3) в (8.2). Получим:
(8.4)
или с учетом первой теоремы:
(8.5)
Расстояние О1 О2 межосевое
расстояние.
Точку
обозначим
Р.
пересечения общей нормали n - n с О1 О2
подобны.
Полученные треугольники О1 KP и О2 LP
Следовательно:
или с учетом (8.5):
Выражение (8.6) - основная теорема зацепления.
196.
Общая нормаль в точке касания звеньев высшейкинематической пары делит межосевое расстояние на отрезки
обратно пропорциональные угловым скоростям.
Отношение w
угловых скоростей звеньев при передаче
1
w2
движения от звена 1
отношением i12 .
к звену 2 называется
передаточным
197.
198.
Из равенства (8.6)i12
1 O2 P
2 O1 P
следует: чтобы при
зафиксированных центрах О1 и О передаточное
отношение
2
было постоянным необходимо, чтобы нормаль всегда (в любом
положении звеньев) проходила через одну и ту же точку Р. Эта
точка оказывается неподвижной в пространстве и называется
полюсом зацепления.
Проведем окружности радиусами О1 P и О2 P .Эти окружности
называются начальными. Они касаются и перекатываются одна по
другой без скольжения.
Эвольвента окружности и ее свойства
Свойства зубчатого механизма во многом определяются выбором
типа кривых, по которым очерчиваются боковые поверхности
зубьев. Выбор же кривых должен, прежде всего, для любых
зубчатых колес удовлетворять основной теореме зацепления. Число
таких кривых весьма ограничено. В настоящее время в
машиностроении основной кривой для профилей зубьев является
эвольвента окружности, предложенная Л.Эйлером в 1754 г.
199.
Эвольвентой окружности называется кривая, описываемаяточкой прямой линии, перекатываемой по окружности без
скольжения.
200.
Построим эвольвенту. Проведем окружность. Через точку Апроведем касательную. От точки А отложим на касательной
одинаковые отрезки А 1 , 1 2
, 2 3 и т. д., а на окружности одинаковые дуги А 1 , 1 2 , 2 3 и т. д. При этом
отрезки равны соответствующим дугам: А 1 = А 1 ,
1 2 = 1 2 , 1-2= 2 3 и т.д.. В точках 1 , 2 , 3
и т. д.
проводим касательные и откладываем на них от данных точек
отрезки, равные А 1 , А 2 , А 3 и т. д. Соединяем
полученные точки А, А1 ,А2 ,А3 , и т. д. плавной кривой и получаем
эвольвенту.
Окружность, по которой перекатывается прямая при
образовании эвольвенты, называется основной окружностью.
Прямая, перекатываемая по окружности, называется
образующей прямой.
201.
Свойства эвольвенты• Образующая прямая всегда нормальна к эвольвенте и является
касательной к основной окружности.
• Длина нормали равна радиусу кривизны эвольвенты и
соответствующей дуге окружности.
• Эвольвента начинается на основной окружности и всегда
расположена вне ее.
• Эвольвента является кривой без перегибов.
• Форма эвольвенты зависит от радиуса основной окружности.
202.
Геометрические характеристики эвольвентногозубчатого колеса
Окружность вершин - окружность, описанная из центра колеса и
ограничивающая вершины зубьев.
Окружность впадин - окружность, описанная из центра колеса и
ограничивающая его впадины со стороны колеса.
Делительная окружность - окружность, на которой расстояние
между одноименными сторонами двух соседних зубьев равно шагу
зуборезного инструмента. Делительные окружности совпадают с
начальными, если межосевое расстояние пары зубчатых колес равно
сумме радиусов делительных окружностей.
Модуль - значение следует выбирать по СТ СЭВ-310-76. Этим
стандартом дан ряд значений от 0,05 до 100 мм:
203.
- 1 ряд (предпочтительный): 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12;16; 20; 25 и т. д.;- 2 ряд: 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5;
7; 9; И; 14; 18; 22 и т. д.
Окружной шаг зубчатого зацепления р – есть расстояние между
одноименными точками двух соседних зубьев колеса, измеренное
по дуге делительной окружности.
Высотой зуба h – называется радиальное расстояние между
окружностью вершин и окружность впадин.
Разница в высоте ножки зуба одного колеса и высоте головки зуба
другого необходима для образования радиального зазора:
c h fi ha2 0,25m
204.
Теоретически толщина зуба s и ширина впадины e по делительнойокружности равны между собой:
s e p/2
Однако, чтобы создать боковой зазор, необходимый для
нормальной работы зубчатой пары, зуб делается несколько тоньше,
вследствие чего он входит во впадину свободно.
Межосевое расстояние двух сцепляющихся зубчатых колес
определяется по формуле:
z1m z 2 m
a w r1 r2
m z1 z 2 / 2
2
2
Передаточное отношение:
i12
O2 P r2 2 z2 m z2
O1 P r1 2 z1 m z1
(8.7)
205.
206.
№п/п
Название
1
Диаметр окружности вершин
2
Диаметр окружности впадин
3
Диаметр основной окружности
4
Диаметр начальной окружности
5
Диаметр делительной окружности
6
Модуль
m
7
Число зубьев
z
8
Шаг по делительной окружности
9
Высота зуба
10
Высота головки зуба
11
Высота ножки зуба
12
Толщина зуба по делительной окружности
13
14
Ширина впадины между зубьями по
делительной окружности
Угловой шаг
Формула для вычисления
(без смещения режущего инструмента)
d a m z 2
d f m z 2,5
d в mz cos 20 0
d w mz
d mz
p m
h 2,25m
ha m
h f 1,25m
s p/2
e p/2
2
z
207.
Эвольвентное зубчатое зацеплениеПостроим два зубчатых колеса, находящихся в зацеплении
(рис.9.1). Для этого отложим межосевое расстояние О1О2 , равное
сумме радиусов начальных окружностей, а из центров О и О2
1
проведем эти окружности. Начальные окружности касаются друг
друга в полюсе Р. Через полюс Р проведем прямую,
перпендикулярную О1О2 . Затем под углом 20 0 (для
нормального зубчатого зацепления) проведем прямую N-N, на
восстановим перпендикуляры
которую из центров
и
1
2
О1 А и О2 Р. Радиусами О1 А и О2 В
проводим
основные
окружности. На отрезке АВ возьмем произвольную точку К.
Если прямую N-N катать без скольжения по первой основной
окружности, а затем по второй, то точка К опишет в начале
эвольвенту Э1 , а затем эвольвенту Э2 , которые примем за
боковые профили зубьев зубчатых колес.
О
О
208.
На основании свойства эвольвенты прямая N-N являетсяодновременно нормалью эвольвент Э и Э
и, следовательно,
2
1
должна проходить через точку их касания К. По-другому общая
нормаль к эвольвентам не может пройти , так как должна касаться
основных окружностей.
Линия N-N представляет собой геометрическое место точек
касания зубьев и называется линией зацепления.
Вне этой линии зубья не контактируют. Прямая N-N не меняет
своего положения и всегда пересекает межосевое расстояние О1О2
в полюсе Р. По основной теореме зацепления передаточное
отношение для зубчатого механизма
O2 P
i12
O1 P
является постоянной величиной.
209.
Установим границы линии зацепления. Участок АВ называетсятеоретической частью линии зацепления. Первой точкой
зацепления колес будет точка а – точка пересечения окружности
вершин 2 колеса с линией зацепления N-N. Последней будет
находиться в зацеплении точка пересечения окружности вершин 1
колеса с линией зацепления.
Участок ab называется рабочий участок линии зацепления.
Дуги
начальных
окружностей
между
положениями
соответствующих профилей зубьев в начале и конце зацепления для
каждого из колес называются дугами зацепления.
Угол называется углом зацепления.
210.
Определение длины рабочего участка линии зацепленияИз рис. 8.1 очевидно, что:
аb=аР+Рb
(9.1)
Рb=Аb–АР
(9.2)
Аb = ra2 rb2 ;
АР = r sin
(9.3)
b1
Подставляя выражение (9.3) в (9.2) получим:
1
Рb
ra21 rb21 -
1
rb1 sin
(9.4)
Аналогично можно получить:
Рa
ra22 rb22 - rb
sin
(9.5)
Подставляя (9.4) и (9.5) в (9.1), получим длину рабочего участка
линии зацепления:
2
2
2
2
аb = ra1 rb1 +
sin
r
r
r
r
b
(
2 ) *
a2
b2
b1
(9.6)
2
211.
Рис.9.1212.
Определение длины дуги зацепленияДуга зацепления с d лежит на начальной окружности (рис.9.2).
1 1
Ее длина равна:
(9.7)
с d = r
1 1
Дуга с 0 d 0 лежит на основной окружности. Ее длина равна:
с d = r
(9.8)
Выразим из (9.8) центральный угол и, учитывая, что
rb = r cos , получим
0
0
b
ñ0 d 0
=
r cos
(9.9)
Подставим (9.9) в (9.7), получим:
с0 d 0
с1d1 = cos
213.
Из свойств эвольвенты следует, чтос 0 d 0 = А d 0 - А с 0
= Аb – Аа = аb
Тогда:
ab
с1d1 = cos
(9.10)
Рис. 9.2
214.
Качественные показатели зубчатого зацепления• Коэффициент перекрытия
Характеризует
такие
важнейшие
свойства
процесса
зацепления, как его непрерывность и продолжительность.
с1d1
Определяется по формуле: =
Р
или с учетом (9.10):
=
ab
p cos
(9.11)
Коэффициент перекрытия показывает среднее количество пар
зубьев, находящихся одновременно в зацеплении.
215.
Если = 1 – в зацеплении находится одна пара зубьев; = 2 – взацеплении находится две пары зубьев; = 1,7 – в зацеплении 70 %
времени находится две пары зубьев и 30 % времени одна пара
зубьев.
При проектировании принимают min = 1,05, обеспечивающее
зацепление с 5 % запасом.
Коэффициент перекрытия можно увеличить:
а) заменой прямозубых передач на косозубые, у которых =
8÷10;
б) увеличением числа зубьев z и уменьшением модуля m.
• Коэффициент удельного давления
Учитывает влияние геометрии зубьев (радиусов кривизны их
профилей) на величину контактных напряжений, возникающих
в местах соприкосновения зубьев. Чем больше радиусы кривизны,
тем меньше контактные напряжения.
216.
Определяется по формуле:m
=
пр
,
где m – модуль;
пр
1 2
1 2
(9.12)
- приведенный радиус кривизны эвольвентных
профилей в точке К контакта.
Часто для определения коэффициентов используют специальные
диаграммы. Построим такую диаграмму.
217.
Разобьем участок АВ (рис.9.3) на 4 равных отрезка. Тогда всоответствующих точках, учитывая свойства эвольвенты АВ ,
получим:
1
№ Точка
Радиус
кривизны
1
1
В
2
1
3
2
4
3
5
А
Радиус кривизны
2
Приведенный
радиус кривизны
пр
2
218.
Диаграмма позволяет найти в любой момент зацепления.Рис. 9.3
219.
• Коэффициент относительного скольженияРабочие участки профилей зубьев перекатываются друг по другу
со скольжением. Величина скольжения определяет износ зубьев,
потери мощности на скольжение.
Характеристикой вредного влияния скольжения являются
коэффициенты
коэффициенты
относительного
1 и 2 скольжения.
Для нахождения коэффициентов 1 и 2 рассмотрим пару
зубчатых колес, зубья которых соприкасаются в точке К (рис.9.4).
Скорости точки К:
V1к w1 О1 К
;
V1ê Î 1Ê
V2к w2 О2 К
;
V2 к О2 К
220.
Проекции этих скоростей на общую нормаль равны (1 теорема);проекции на касательную различны:
V w1 1
r
1к
V2rк w2 2 ,
где
1 АК , 2=ВК – радиусы кривизны к профилям.
221.
NB
K
V2K
V1K
O1
O2
P
w2
w1
A
N
Рис. 9.4
222.
Скорость скольжения первого профиля по второму:VS1 2 VK 1 V
K2
Скорость скольжения второго профиля по первому:
VS2 1 VK 2
VK1
Обычно пользуются понятием относительного скольжения:
1
VS1 2
VK1
и
2
VS2 1
VK 2
Подставляя значения скоростей, выраженные через w и ,
получим:
w1 1 w2 2
w2 2
w2 2 w1 1
w1 1
1
1
2
1
;
w1 1
w1 1
w2 2
w2 2
(9.13)
223.
Покажем график зависимости 1 и 2 отположения
контакта зубьев на линии зацепления.
Вычислим в характерных точках линии зацепления.
1
№
Точка
1
А
2
Р
3
В
Радиус кривизны
1
Радиус кривизны
2
При определении 1 в полюсе Р учитывали, что
2r 2
2r 1
z2
;
;
z1
m
m
; ВР = r 2 sin
АР =
r 1 sin
Тогда
1 1
r 2 sin
r 1 sin
График показан на рис. 9.5.
2 r 1
m 0
2 r 2
m
точки
Коэффициент
1
224.
Рис 9.5225.
ЛЕКЦИЯ 9Краткое содержание
1. Эвольвентное зубчатое зацепление.
2. Линия зацепления.
3. Дуга зацепления.
4. Определение ее длины.
5. Качественные показатели зубчатого зацепления.
6. Коэффициент перекрытия.
7. Коэффициент удельного давления.
8. Коэффициент относительного скольжения.
226.
ЛЕКЦИЯ 10Краткое содержание
1. Методы изготовления эвольвентных зубчатых колёс.
2. Исходный и рабочий контуры режущего инструмента.
Станочное зацепление.
3. Смещение исходного контура.
4. Определение минимального числа зубьев зубчатого колеса.
Явление подреза зубьев.
5. Геометрические размеры эвольвентного зубчатого колеса
изготовленного со смещением исходного контура.
227.
Методы изготовления эвольвентных зубчатых колёсВ основу изготовления эвольвентных зубчатых колёс положено
два принципиально отличительных метода.
Способ копирования
Рабочие кромки инструмента по форме соответствуют
обрабатываемой поверхности (подобны ей, то есть заполняют эту
поверхность как отливка заполняет форму).
Нарезание зубчатых колес осуществляется профилированной
пальцевой 1 или дисковой 2 фрезами (рис.10.1 а, б), проекция
режущих кромок которых соответствует конфигурации впадин.
Резание производится в следующем порядке: прорезается впадина
первого зуба, затем заготовка с помощью делительного устройства
(делительной головки) поворачивается на угловой шаг и
прорезается следующая впадина. Операции повторяются до тех пор,
пока не будут прорезаны все впадины.
228.
Достоинства:1.Возможность нарезания зубьев 6 на универсальном фрезерном
оборудовании.
Недостатки:
1.Огромная номенклатура режущего инструмента (равна сочетанию
модуля и числа зубьев);
2.Принципиальная неточность нарезания зубьев;
3.Нетехнологичность инструмента, малая производительность.
229.
Способ огибания (обкатки)Инструмент и заготовка за счет кинематической цепи станка
выполняют два движения - резания и огибания (под огибанием
понимается такое относительное движение заготовки и
инструмента, которое соответствует станочному зацеплению, т. е.
зацеплению инструмента и заготовки с требуемым законом
изменения передаточного отношения). Нарезание зубчатых колес
осуществляется на зубодолбёжных станках долбяками 3,
гребенками 4 (рис. 10.1 в, г) или на зубофрезерных станках
червячными фрезами.
Достоинства:
1.Принципиальная точность нарезания зубьев;
2.Резкое сокращение номенклатуры и технологичность
инструмента;
3.Высокая производительность.
Недостатки:
1.Требуется специальное зубонарезное оборудование.
230.
Рис.10.1231.
Исходный контур. Рабочий контурПри изготовлении зубчатых колес по методу обкатки режущий
инструмент (долбяк, гребенка, червячная фреза) выполняет
возвратно-поступательное технологическое движение. При этом
режущие кромки инструмента описывают зубчатую поверхность.
Рассечем
эту
воображаемую
поверхность
плоскостью,
перпендикулярной оси нарезаемого колеса. В сечении получим
линию зубчатой формы, называемую исходным контуром (рис.10.2
а). Физический смысл исходного контура состоит в том, что он
является тем следом, который режущая кромка инструмента
оставляет на материале изготовляемого колеса.
232.
а).б).
Рис.10.2
233.
Исходный контур положен в основу стандартизации зуборезногоинструмента.
По ГОСТ 13755-81 значения параметров исходного контура
должны быть следующими:
• профильный угол ;
• шаг зубьев р;
• модуль – m;
• коэффициент высоты головки зуба h*a=1;
• глубина захода hl=2 h*a m;
• радиус кривизны переходной кривой =c*/(1-sin )=0,38;
• коэффициент радиального зазора c*=0,25.
234.
Для обеспечения плавного вхождения зубьев в зацепление иснижения динамических нагрузок на вершине зубьев исходного
контура преднамеренно отступают от теоретической эвольвентной
формы, выполняя срез профиля – фланк (рис.10.2 б). Контур с
фланком называют рабочим контуром.
Требуемые параметры зубчатых колес могут быть получены
соответствующим расположением заготовки зубчатого колеса по
отношению к исходному контуру.
Прямая, на которой теоретическая толщина зуба равна
ширине впадины называется делительной прямой исходного
контура (ДП).
Окружность на которой шаг равен шагу исходного контура,
называют делительной.
235.
Делительная прямая исходного контура и делительная окружностьзаготовки зубчатого колеса могут иметь различное взаимное
расположение. Смещение обычно выражается в долях модуля xm,
где x- коэффициент смещения исходного контура.
Возможны три случая относительного расположения делительной
прямой и делительной окружности радиуса r.(рис.10.3).
• Делительная прямая располагается на расстоянии от оси колеса,
большем чем его радиус r. Зубчатые колеса, изготовленные при
таком условии, называются положительными.
• Делительная прямая касается делительной окружности, х=0.
Зубчатые колеса, получаемые при этом, называются нулевые.
• Делительная прямая располагается на расстоянии от оси колеса,
меньшем, чем его радиус r. Зубчатые колеса, получаемые при этом
называются отрицательные.
236.
Рис.10.3Форма зубьев колес, нарезанных с различным смещением
инструмента, показана на рис.10.4. Смещение изменяет форму зуба.
Так, положительное смещение приводит к утолщению зуба у
основания и уменьшению кривизны профиля. Такое изменение
формы способствует повышению его прочности. Выбор того или
иного смещения зависит от назначения зубчатой передачи, условий,
в которых она работает, нагрузок на элементы зубчатой передачи и
т.д.
237.
Рис.10.4В зацепление можно вводить зубчатые колеса, изготовленные с
различным сдвигом режущего инструмента. Возможны следующие
сочетания:
X= X1 + Х2 > 0 - положительное зацепление;
X= X1 + Х2 = 0 - нулевое зацепление;
X= X1 + Х2 < О - отрицательное зацепление.
238.
Минимальное число зубьев зубчатого колеса, изготовленногобез смещения и со смещением исходного контура
Зацепление рабочего контура инструмента с нарезаемой
заготовкой, осуществляемое в процессе нарезания по способу
огибания, называется станочным зацеплением.
Согласно свойствам эвольвентного зацепления рабочий контур и
эвольвентная часть профиля зуба нарезаемого колеса располагаются
касательно друг к другу только на линии зацепления, начинающейся
в точке А (рис. 10.5). Левее этой точки (в А1) рабочий контур не
касается эвольвентного профиля зуба колеса, а пересекает его. Это
приводит к подрезанию зуба у его основания (рис. 10.4), а впадина
между зубьями нарезаемого колеса получается более широкой.
Подрезание уменьшает эвольвентную часть профиля зуба, что
приводит к сокращению продолжительности зацепления каждой
пары проектируемой передачи) и ослабляет зуб в опасном сечении.
Поэтому подрезание не допустимо.
239.
Рассмотрим различные положения заготовки колеса и рабочегоконтура (рис.10.5):
• 1 положение
Прямая вершин пересекает линию зацепления N-N в точке А1,
расположенной вне теоретической линии зацепления АВ.
• 2 положение
Прямая вершин проходит через крайнюю точку А линии
зацепления.
• 3 положение
Отодвинем рабочий контур на величину xm. Прямая вершина
пройдёт через точку А2.
Построим эти положения рабочего контура на рис.10.5.
Во всех трёх случаях полюс зацепления Р при сдвиге рабочего
контура не изменял своего положения
В первом положении зубья зубчатого колеса будут подрезаны.
240.
Явление подрезов зубьев наблюдается в том случае, если рабочийучасток линии зацепления аb выходит за пределы теоретического
АВ.
Во втором положении случае зубья зубчатого колеса не будут
подрезаны
При этом должно выполняться условие: PA PA2
. (10.1)
Используя условие (10.1) определим минимальное число зубьев z
колеса, при котором они не будут подрезаны. Из треугольника РАО
следует, что (10.2)
Из
треугольника
РА2С2
следует,
что
(10.3)
Подставляя выражения (10.2) и (10.3) в условие (10.1) и решая его
относительно z, получим:
(10.4)
241.
Если х=0, то из выражения (10.4) найдем минимальное числозубьев колеса без смещения, которые не будут подрезаны режущим
инструментом:
2ha
z min
sin 2
,
(10 .5)
a
Для стандартного зубчатого колеса при h 1 , , z min =17.
Для уменьшения габаритов зубчатых передач колеса следует
проектировать с малым числом зубьев.
Поэтому при z<17, чтобы не произошло подрезания колеса
должны быть изготовлены со смещением инструмента. Выясним,
каково же минимальное смещение, при котором не получается
подрезания зубьев. Оно определяется из условия (10.1)
242.
2Подставляя сюда значение sin из уравнения (10.5) и
решая относительно х , запишем
ha * ( z min z )
x
z min
(10.6)
При ha*=1 и zmin=17 получим
x
17 z
17
(10.7)
Формула (10.7) позволяет определять требуемую величину
коэффициента смещения рабочего контура
для нарезания
желательного числа зубьев z без их подреза.
243.
Геометрические размеры эвольвентного зубчатого колеса,изготовленного со смещением исходного контура
• Толщина зуба по длительной окружности
S
m
2
2 xm tg
• Диаметр окружности впадин
d f m( z 2,5) 2 xm
• Диаметр окружности вершин
d a ( z 2) 2 xm ym
• Высота зуба
h 2,25m ym
ha m (1 x) ym
h f m (1,25 x)
где
y - коэффициент уравнительного смещения.
244.
Рис.10.5245.
ЛЕКЦИЯ 11Краткое содержание.
1. Многоступенчатые зубчатые механизмы.
2. Кинематика коробки передач.
3. Дифференциальные зубчатые механизмы.
4. Метод обращённого движения.
5. Кинематика автомобильного дифференциала.
6. Планетарные зубчатые механизмы. Примеры.
246.
Многоступенчатые зубчатые механизмыСложные зубчатые механизмы состоят из нескольких пар
зубчатых колёс.
Зубчатые механизмы, служащие для уменьшения числа оборотов
ведомого вала по сравнению с ведущим, называются редукторами.
Зубчатые механизмы, служащие для увеличения числа оборотов
ведомого вала по сравнению с ведущим, называются
мультипликаторами.
247.
Определение передаточных отношений многоступенчатыхзубчатых механизмов
В общем случае, когда передача движения осуществляется с
помощью n пар зубчатых колёс и количество валов равно n+1,
передаточное отношение определяется по формуле:
i1( n 1) ( 1) (i12 i23 i34 in( n 1 )
k
где k-количество
зацеплением.
простых
зубчатых
передач
с
(11.1)
внешним
248.
Пример11.1.
Определить
передаточное
отношение
многоступенчатой зубчатой передачи (рис.10.1). Число зубьев
зубчатых колёс: z1=15, z2=30, z 2 =12, z3=24, z 3 =14, z4=28, z4 18 ,
z5=36.
Решение:
Количество простых зубчатых передач с внешним зацеплением
k= .
По формуле (11.1):
Рис.11.1
249.
Пример11.2.
Определить
передаточные
отношения
многоступенчатой зубчатой передачи (рис.11.2).
Решение:
Количество простых зубчатых передач с внешним зацеплением
k= .
По формуле (11.1) вычисляем:
Рис.11.2
250.
Из примера видно, что на величину передаточного отношенияпромежуточные колёса 2 и 3 не оказывают никакого влияния. Такие
промежуточные колёса называются паразитными. Они применяются
для изменения направления вращения или при передаче движения
при большом межосевом расстоянии.
Знак минус показывает, что ведущее и ведомое колёса вращаются
в разные стороны.
251.
Кинематика коробки передачКоробкой передач - это зубчатый механизм, передаточное
отношение которого можно изменить скачкообразно.
Коробками передач снабжают все машины, рабочие органы
которых должны вращаться с различными скоростями в
зависимости от условий работы.
В автомобиле коробка передач служит для изменения крутящего
момента. передаваемого от коленчатого вала двигателя к
карданному валу, для движения автомобиля задним ходом и
длительного разобщения двигателя от трансмиссии во время
стоянки автомобиля и при движении его по инерции.
Во время трогания автомобиля с места, при движении на подъем с
грузом крутящий момент на колесах должен быть большим, чем при
движении по горизонтальному участку дороги.
252.
Пример 11.3. Определить скорости ведомого вала в коробкепередач (рис.11.3). Коробка передач состоит из картера, ведущего
вала с шестерней, ведомого вала, промежуточного вала, оси
шестерни заднего хода, набора шестерен и механизма
переключения.
Дано: z1= , z2= , z3= , z4= , z5= , z6= , z7= , z8= , z9=
, z10= .
Число оборотов ведущего вала 1 n1=1000 об/мин.
Решение:
Данная коробка передач имеет 4 передачи для движения вперед и
одну передачу заднего хода. В постоянном зацеплении находятся
шестерня ведущего и промежуточного валов, шестерни 2 и 3
передач промежуточного и ведомого валов.
253.
254.
Первая передача (рис.11.4,а)включается перемещением шестерни первой передачи ведомого
вала назад до зацепления с шестерней первой передачи
промежуточного вала.
Вторая передача (рис.11.4,б) включается перемещением
шестерни первой передачи ведомого вала вперед до зацепления с
шестерней
постоянного
зацепления
второй
передачи
промежуточного вала.
Третья передача (рис.11.4,в) включается перемещением муфты
синхронизатора назад. Зубья муфты входят в зацепление с венцом
шестерни постоянного зацепления третьей передачи, закрепляя ее
на ведомом валу.
Четвертая передача (рис.11.4,г)
включается перемещением муфты синхронизатора вперед, ее
зубья входят в зацепление с венцом ведущего вала, соединяя
ведущий и ведомый валы. Промежуточный вал в передаче
крутящего момента не участвует.
255.
Задний ход (рис.11.4, г) включается перемещением блокашестерен заднего хода на оси до ввода в зацепление с шестернями
первой передачи промежуточного и ведомого валов.
256.
Рис.11.4257.
Для каждой из передач определяем передаточное отношение i1-2по (10.1), число оборотов ведомого вала n2 = n1/i1-2 и крутящий
момент. Результаты расчётов приведены в таблице.
Передача
1
2
3
4
Заднего хода
Зубчатые колеса,
передающие
движение
Число
оборотов
Передаточное отношение
ведомого вала
n2
Крутящий
момент
258.
Дифференциальные механизмыДифференциальные механизмы имеют зубчатые колёса с
подвижными осями (рис.11.5).
Зубчатое колесо 1 называется центральным колесом, колесо 2,
имеющее подвижную ось, – сателлитом, а звено H, несущее
сателлит, – водилом. Число степеней подвижности механизма
находим по формуле Чебышева
W= 3n-2p1-p2= 3 3 2 3 1 2 ,
здесь n=3 – число подвижных звеньев (колёса 1 и 2 водило H),
p1=3 – число одноподвижных кинематических пар (стойка –
колесо 1, стойка - водило H и водило H – колесо 2,
p2=1
число
двухподвижных
кинематических
пар
(зубья колёс 1 и 2).
259.
В данном механизме два независимых закона движения, т.е. двумзвеньям можно задать произвольные законы движения, тогда звено
2 будет двигаться по определённому закону.
Рис.11.5
260.
Метод обращённого движенияДифференциальные
механизмы
не
имеют
постоянного
передаточного отношения. Передаточное отношение можно
определить, используя метод обращённого движения (метод
Виллиса). Для этого дифференциальному механизму придаём
дополнительную угловую скорость, равную угловой скорости
водила
H , но направленную противоположно. Это не
изменяет относительного движения звеньев, абсолютные же
скорости будут другими.
Звено
1
Скорость
движении
при
2
1
Скорость звена
обращённом
1
Н
2
- н
2
н
- н
0
261.
Такой дифференциальный механизм называетсяпреобразованным, для которого справедливо отношение:
1
1 H
z2
i12
2
2 H
z1
(11.2)
Если в дифференциальном механизме имеется n зубчатых колёс:
1 H
i1 n
=
n H
n1 n H
nn n H
(11.3)
262.
Кинематика автомобильного дифференциалаПри помощи дифференциального механизма (рис.11.6) в
автомобилях осуществляется передача вращательного движения от
двигателя к ведущим колёсам. При повороте дифференциальный
механизм распределяет мощности между ведущими колёсами таким
образом, чтобы их обороты согласовывались с условиями движения.
Дифференциальный механизм состоит из центральных
конических колёс 3 и 4, конического колеса – сателлита 5 и водила
2. Водило выполнено в виде конического колеса и передача
вращения водилу осуществляется от карданного вала 1 при помощи
обычной конической передачи 1 – 2. На основании (11.2):
(11.4)
263.
Формула (11.4) связывает обороты водила n2 и обороты левого иправого колёс. Число оборотов n2 является известным. Если машина
движется прямолинейно, то равенству к (11.4) добавляется n3=n4.
При повороте к равенству (11.4) добавляется:
R B
(11.5)
n3
2
n4 R B
2
Равенство (11.4) и (11.5) позволяют получить определённость
решения и найти n3 и n4 .
264.
Рис.11.6265.
Планетарные механизмыЕсли у дифференциального механизма центральное колесо 1
сделать неподвижным и тем самым отнять одну степень
подвижности, то можно получить зубчатый механизм с одной
степенью подвижности (рис.11.7).
Зубчатые механизмы со степенью подвижности W 1 ,
у которых геометрические оси некоторых колёс перемещаются,
называются планетарными механизмами.
Найдём передаточные отношения. Рассматривая планетарный
механизм как частный случай дифференциального механизма и
полагая
, можно применить формулу (11.3). Получим:
1
0
H
1 H
=
i1 n
n H n H
266.
Обратное передаточное отношениеn
1 H n
in 1
1
i1 n
H
H
, где
n
inH
- передаточное отношение от вала любого колеса n к
H
валу водила H.
inH 1 in 1
Следовательно, in 1 1 i nH или
(11.6)
Отметим, что к формуле (10.6) под цифрой 1 обозначено
неподвижное колесо. Это необходимо учитывать и корректировать
формулу при решении задач.
267.
Рис.11.7268.
Пример 11.4Определить передаточное отношение планетарного механизма
(рис.11.8).
Дано: z1=100, z2=99,
2 =100, z3=101.
z
Рис.11.8
269.
Решение:По формуле (11.6) определим передаточное отношение (учтём,
что здесь неподвижным является колесо 3):
Как видно, передаточное отношение здесь очень мало. Вал 1
вращается в 10 000 раз медленнее, чем вал водила. Для
осуществления такого малого передаточного отношения при
помощи обычного зубчатого механизма необходимо было бы
сделать его многоступенчатым, что потребовало бы большого
количества колес. Однако необходимо отметить, что при таких
передаточных отношениях планетарный механизм может надежно
работать только в сторону уменьшения числа оборотов ведомого
вала по сравнению с ведущим, т. е. может передавать движение от
водила к колесу.
270.
При передаче движения в сторону увеличения числа оборотовмеханизм при таких передаточных отношениях обладает очень
низким к. п. д. и даже может быть самотормозящим, т. е. не может
даже двигаться. Поэтому при очень малых передаточных
отношениях планетарные передачи применяются только в
маломощных механизмах, работающих в течение небольших
промежутков времени (например, в приборах дистанционного
управления). Большим достоинством планетарных механизмов,
помимо возможности достижения больших передаточных
отношений, является соосность ведущего и ведомого валов лёгкость
и компактность конструкции.
271.
Пример 11.5Определить передаточное отношение планетарного механизма
(рис.11.9) от вала двигателя 1 к валу винта самолёта H и число
оборотов винта nH , если число оборотов двигателя n =3000
1
об./мин., а количество зубьев зубчатых колёс равно: z1=66 , z2=18 ,
z3=30.
Решение:
Передаточное отношение
планетарного механизма:
Число оборотов винта:
Рис.11.9
272.
ЛЕКЦИЯ 12Краткое содержание
• Область применения кулачковых механизмов.
• Классификация кулачковых механизмов.
• Законы движения ведомых звеньев.
• Кинематическое и динамическое условия.
• Жесткие и мягкие удары.
• План скоростей.
• Определение угла давления δ.
• Определение минимального радиуса кулачка.
273.
Кулачковые механизмы применяются во многих приборах(программных, счетно-решающих, самопищущих автоматах) и
машинах (станки, двигатели). В большинстве случаев кулачковый
механизм состоит из трех звеньев: стойки, кулачка, и ведомого звена
– толкателя, коромысла (рис.13.1). Для уменьшения потерь на
трение и износ профиля кулачка ведомое звено снабжают роликом,
катящимся по профилю. К конструкции кулачкового механизма
предъявляют ряд требований: механизм должен иметь габариты;
ограниченные динамические нагрузки; максимальный коэффициент
полезного действия; входящие в него звенья должны обладать
достаточной прочностью и износостойкостью.
274.
Рис.12.1275.
Достоинства кулачковых механизмов:• Воспроизведение ведомым звеном неравномерного движения по
какому-то заданному закону, с остановками определенной
продолжительности.
Недостатки кулачковых механизмов:
• Сложность изготовления;
• Быстрый износ профиля кулачка, вызывающий изменение закона
движения ведомого звена и снижение точности механизма.
276.
Классификация рычажных механизмовПо характеру движения
• Плоские (рис.12.1, а, б, в, г);
• Пространственные (рис.12.2 ,а, б).
По виду движения кулачков
• Поступательное (рис.12.1,в.г);
• Вращательное (рис.12.1,а.б).
По взаимному расположению кулачка и толкателя
• Центральные (рис.12.1,б);
• Дезаксильные (рис.12.1,а.в,г).
277.
По взаимному расположению кулачка и толкателя• Центральные (рис.12.1,б);
• Дезаксильные (рис.12.1,а.в,г).
• По типу замыкания кинематической пары
• С кинематическим замыканием (рис.12.3,а);
• С силовым замыканием (рис.12.3,б,в).
Рис12.2
278.
Рис 12.3279.
Виды толкателей приведены на рис.12.4. Рис.12.4, а – толкатель сроликом, 12.4, б – толкатель грибообразный, 12.4, в – толкатель с
острием, 12.4, г, д – плоские толкатели.
а
б
в
г
д
Рис.12.4
280.
Законы движения ведомых звеньев.Теоретически в кулачковом механизме можно осуществить самые
различные законы движения ведомых звеньев, но на практике
пользуются только теми, которые удовлетворяют кинематическим и
динамическим требованиям к кулачковым механизмам.
Кинематическое условие
Рис.12.5
281.
Кинематическое условие состоят в том, что передача движениямежду кулачком и ведомым звеном возможна только тогда, когда
проекции линейных скоростей точки касания этих звеньев на
общую нормаль равны (лекция 8, первая теорема). (рис.12.5).
Динамическое условие
Пусть кулачок действует на толкатель с некоторой силой Fд (сила
давления). Вектор силы Fд направлен вдоль нормали n-n. (рис.12.6).
Угол между направлениями векторов силы Fд и скорости толкателя
V2 обозначим δ - угол давления. Угол γ =90°-δ -угол передачи
движения.
282.
Сила F=Fд сosδ -сила полезных сопротивлений (сила тяжести,сила инерции, давления в пружине и т.д.). При расчетах сила F
считается известной.
Сила H=Fд sinδ- сила вредных сопротивлений. Вызывает перекос
толкателя, возникновение сил трения в направляющих. Если эта
сила будет очень велика, может произойти заклинивание и поломка
толкателя.
Рис.12.6
283.
Для уменьшения силы H необходимо уменьшать угол давления δ.Однако, с другой стороны, с уменьшением угла δ возрастают
размеры кулачка.
Динамическое условие записывается в виде:
δ≤δmax
(12.1)
Принимают δmax =30°-для поступательно движущихся толкателей;
δmax=45°-для вращающихся толкателей.
284.
Кинематическому и динамическому условиям удовлетворяют тритипа законов движения ведомого звена:
1.Законы, дающие постоянную скорость ведомого звена
(рис.12.7).
За один оборот кулачка (φ=2π) толкатель проходит следующие
фазы: φn-фаза подъема, φвв-фаза верхнего выстоя, φo- фаза
опускания, φнв- фаза нижнего выстоя.
Скорость движения толкателя на фазах подъема и опускания
постоянна. Ускорения на обеих фазах равны нулю, кроме положений
а, в, с, и d, где функция Sz=f(φ1) имеет разрывы. В этих положениях
теоретически ускорения ведомого звена, а, следовательно, и силы
инерции являются равными бесконечности. Это вызывает
появление в механизме так называемых жестких ударов.
Практически, из-за наличия упругих деформаций и зазоров в
кинематических парах ускорения (следовательно и силы инерции)
имеют большую, но конечную величину. Это приводит к
размыканию элементов высшей кинематической пары, соударению
кулачка и толкателя, быстрому износу поверхностей в этих местах.
285.
Применяется данный закон при малых скоростях ведомого звенаили только на части фаз подъема и опускания и в закон вводятся
переходные кривые, позволяющие осуществить плавный переход на
участках сопряжения двух линейных законов.
Рис.12.7
286.
2.Законы, дающие постоянное ускорение ведомого звена(рис.12.8)
В этих законах ускорение в некоторых точках мгновенно
изменяется на конечную величину, вызывая резкое изменение силы
инерции, что ведет к появлению мягкого удара.
Рис.12.8
287.
3.Безударные законы.В этом случае кривая ускорений не имеет точек разрыва ни
первого, ни второго рода (рис.12.9). Закон движения ведомого звена
в этом случае может быть синусоидальным или косинусоидальным.
Такие законы способствуют наибольшей работоспособности и
долговечности кулачкового механизма.
Рис.12.9
288.
Профилирование кулачка для центрального кулачковогомеханизма с острым толкателем
Требуется построить профиль кулачка, который бы обеспечил
движение ведомого звена по заданному закону.
Дано:
S 2 f ( 1 )
закон движения ведомого звена
(рис.12.10), минимальный радиус кулачка rmin , направление
вращения кулачка.
Профилирование осуществляется следующим образом.
1.Делим фазы подъема, верхнего выстоя и опускания на
диаграмме S 2 f ( 1 ) на некоторое количество равных частей.
Фазу нижнего выстоя можно не делить.
289.
2.Находим графически значения перемещений толкателя:S1= S (1 1); S2= S (2 2); ….; Sn= S (n n) ,
где μS масштаб перемещения,
1-1; 2-2…, n-n - ординаты на диаграмме S 2 f ( 1 ) .
3.Радиусом r=rmin проводим окружность и через центр 0 – линию
движения толкателя. (рис.13.11).
4.В соответствии с разметкой углов φ1 на диаграмме S 2 f ( 1 )
из центра 0 проводим лучи. Вдоль лучей, начиная от проведенной
окружности, откладываем отрезки S1,S2,…,Sn.
290.
5.Соединяя полученные точки 1′,2′,…,n′ плавной кривой получимпрофиль кулачка.
Рис.12.10
291.
ωrmin
Рис.12.11
292.
План скоростей кулачкового механизмаСтроится по ранее изложенным принципам графического
кинематического исследования механизмов (рис.12.12).
Вектор скорости точки А2 , принадлежащей толкателю,
,
,
определяется
из векторного уравнения:
;
VA2 VA1 VA2 A1 где
V A1 - вектор скорости точки А1, принадлежащей кулачку,
V A2 A1
- вектор относительной скорости,
V A2 - вектор скорости точки А2 направлен параллельно
линии движения толкателя.
V A1 1 OA
V A A ||τ-τ;
2 1
V A1 OA
293.
Из полюса pV в масштабе μυ проводим векторV A1 . Из конца этого
вектора проводим направление
вектора V A2 A1 , а из полюса pV
направление вектора V . При пересечение этих направлений
A2
получаем треугольник, из которого определяем искомую скорость
V A2 .
Определение угла давления δ
Покажем схему механизма и план скоростей (рис.12.12).
Дополнительные построения состоят в следующем. Через ось
вращения кулачка 0 проведем линию, перпендикулярную
направлению движения толкателя, до пересечения с нормалью n-n в
точке В.
294.
Полученный треугольник АОВ и план скоростей pυab подобны.Следовательно,
dS A dt
dS A
y VA
1 r
1 rdt
r VA
2
1
295.
Рис.12.12296.
Из (12.1) следует:dS A
y
, где d 1 1 dt.
d 1
(12.2)
Из точки А отложим отрезок y в направлении, перпендикулярном
направлению движения толкателя
( влево ). В ту сторону, куда
окажется направленным вектор V
A2 , если повернуть его на 90° по
направлению вращения кулачка. Конец отрезка ( точку k ) соединим
с осью вращения кулачка 0.
297.
Как видно из (рис.13.12) угол между 0k и направлением движениятолкателя - угол давления δ.
Таким образом, для определения угла давления δ не нужно знать
профиль кулачка. Достаточно вычислить у по формуле (13.2) и,
воспользовавшись рассмотренной методикой, графически найти
угол в любом положении толкателя.
Определение размера минимального радиуса профиля кулачка
Известны:
- закон движения толкателя;
- максимальные углы давления при подъеме и опускании
толкателя δmax и δmax′.
298.
Требуется определить положения оси вращения кулачка и rmin.(минимальный размер кулачка)
1. Для всех положений по формуле (13.1) найти у.
2.Отложить эти отрезки от вертикальной линии.
3.Соединим концы отрезков плавной кривой.
4.Провести касательные под углами δmax и δmax′.
Точка пересечения касательных 0 определяет центры вращения
кулачка.
299.
ЛИТЕРАТУРАОсновная:
1.И.И. Артоболевский «Теория механизмов и машин. –М., 1987 г. – 683 с.
2.С.А. Попов, Г.А. Тимофеев «Курсовое проектирование по теории
механизмов механике машин». –Москва, 2002 г. – 362 с.
3.К.В. Фролов «Теория машин и механизмов», для вузов –М., 1998г. – 421
с.
Дополнительная:
1.Баранов Г.Г. Курс теории механизмов и машин– М., 1974 г.-327 с.
2.Гавриленко Г.С. Теория механизмов – «Высшая школа», 1988 г. -544 с.
3.Кожевников С.Н. Теория механизмов и машин. – М., 1972 г.-576 с.
4.Левитский Н.И. Теория механизмов и машин– М.: Наука, 1990 г. -489 с
5.Попык К.Г. Динамика автомобильных и тракторных двигателей. – М.:
Высшая школа, 1970г. – 173 с.
6.Юдин В.А., Петрокас Л.В. Теория механизмов и машин – М., 1977 г. –
289 с.
300.
16. Кинематический анализ механизмов методом планов скоростей с группой Ассура 2 кл.2 пор. 2 вида.
17. Кинематический анализ механизмов методов планов скоростей с группой Ассура 2 кл.
2 пор. 3 вида.
18. Кинематический анализ механизмов методом планов ускорений с группой Ассура 2 кл.
2 пор. 1 вида.
19. Кинематический анализ механизмов методом планов ускорений с группой Ассура 2 кл.
2 пор. 2 вида.
20. Кинематический анализ механизмов методом планов ускорений с группой Ассура 2 кл.
2 пор. 3 вида.
21. Задачи силового расчета механизмов. Силы, действующие на звенья механизма.
22. Условия статической определенности кинематической цепи плоского вида.
23. Определение реакций в кинематических парах групп Ассура 2 кл. 1 вида.
24. Определение реакций в кинематических парах групп Ассура 2 кл. 2 вида.
25. Определение реакций в кинематических парах групп Ассура 2 кл. 3 вида.
26. Теорема Жуковского.
27. Основные формы уравнений движения.
28. Приведение сил и моментов.
29. Кинетическая энергия звеньев механизма.
30. Приведенный момент инерции и массы механизма.
31. Режимы движения механизма и их характеристика.
301.
32. Средняя скорость движения машины и ее коэффициент неравномерности движения.33. Связь между приведенным моментом инерции и коэффициентом неравномерности
движения.
34. Основная теорема зацепления.
35. Эвольвента окружности и ее свойства.
36. Основные параметры зубчатых колес.
37. Влияние смещения инструментальной рейки на параметры зубчатых колес.
38. Явление подрезания профилей зубьев.
39. Аналитическое определение передаточного отношения планетарного редуктора с
одинарным сателлитом.
40. Методы изготовления эвольвентных профилей.
41. Определение передаточного отношения планетарного редуктора с двойным сателлитом
(внешнего и внутреннего зацепления).
42. Определение передаточного отношения планетарного редуктора с двойным сателлитом
внутреннего зацепления.
43. Определение передаточного отношения планетарного редуктора с двойным сателлитом
внешнего зацепления.
44. Синтез планетарного редуктора с одинарным сателлитом.
45. Передаточное отношение зубчатых механизмов с неподвижными осями.
46. Типы и структура кулачковых механизмов.
47. Законы движения ведомых звеньев кулачковых механизмов.
302.
48. Угол давления в кулачковых механизмах.49. Трение в поступательной кинематической паре.
50. Трение во вращательной кинематической паре.
51. Трение в поступательной паре, выполненной в виде желоба.
52. Сила трения верчения во вращательной кинематической паре.
53. Трение качения и скольжения в высших парах.
54. Уравновешивание механизмов и балансировка роторов.
Основные понятия и определения.
55. Уравновешивание механизмов. Метод замещающих масс.
56. Балансировка роторов. Виды неуравновешенности роторов.
57.
Балансировка
роторов
при
различных
видах
неуравновешенности.
58. Исследование движения механизма с учетом упругости звеньев.
59. Основные методы виброзащиты.
60. Динамическое гашение колебаний.












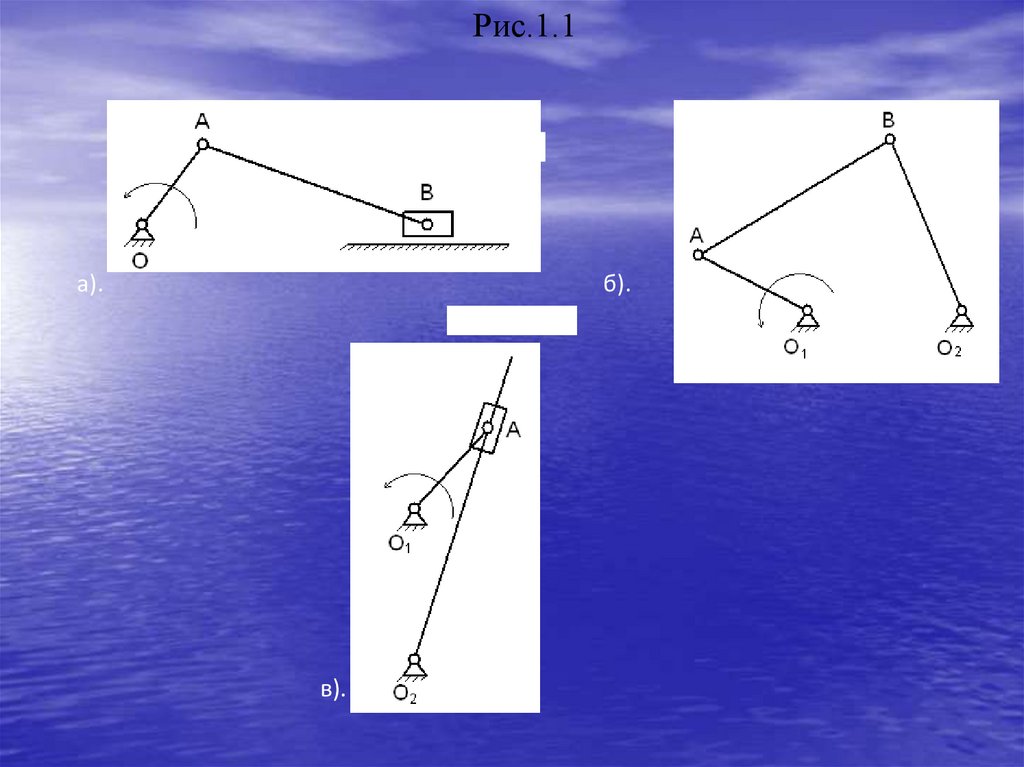


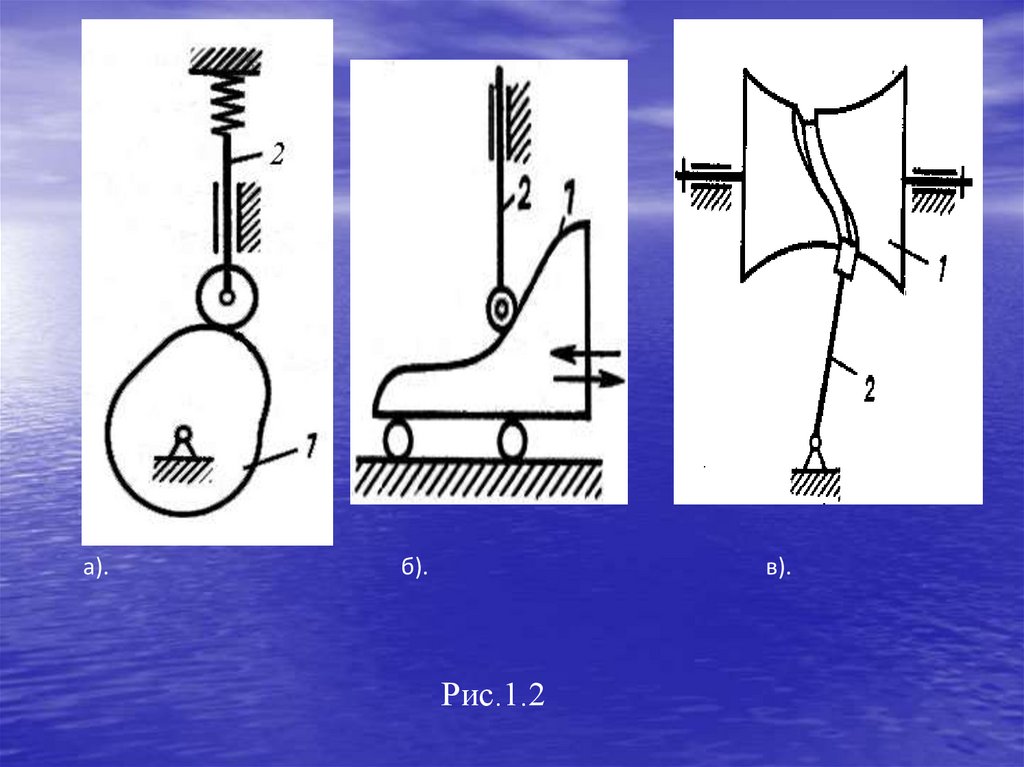



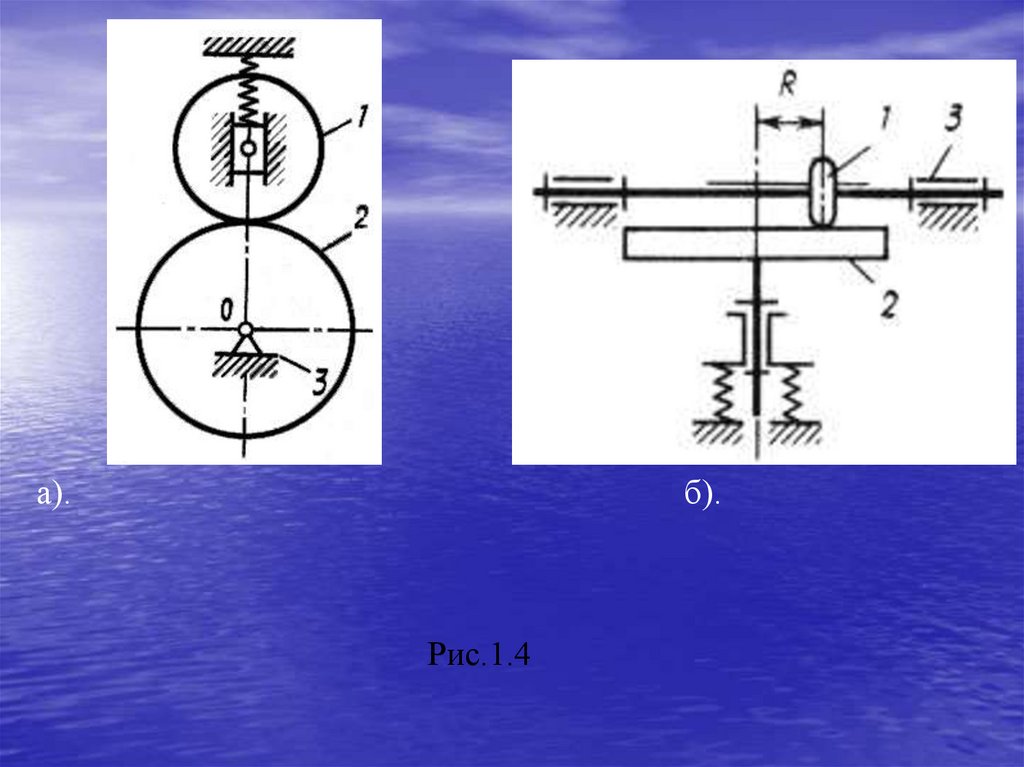



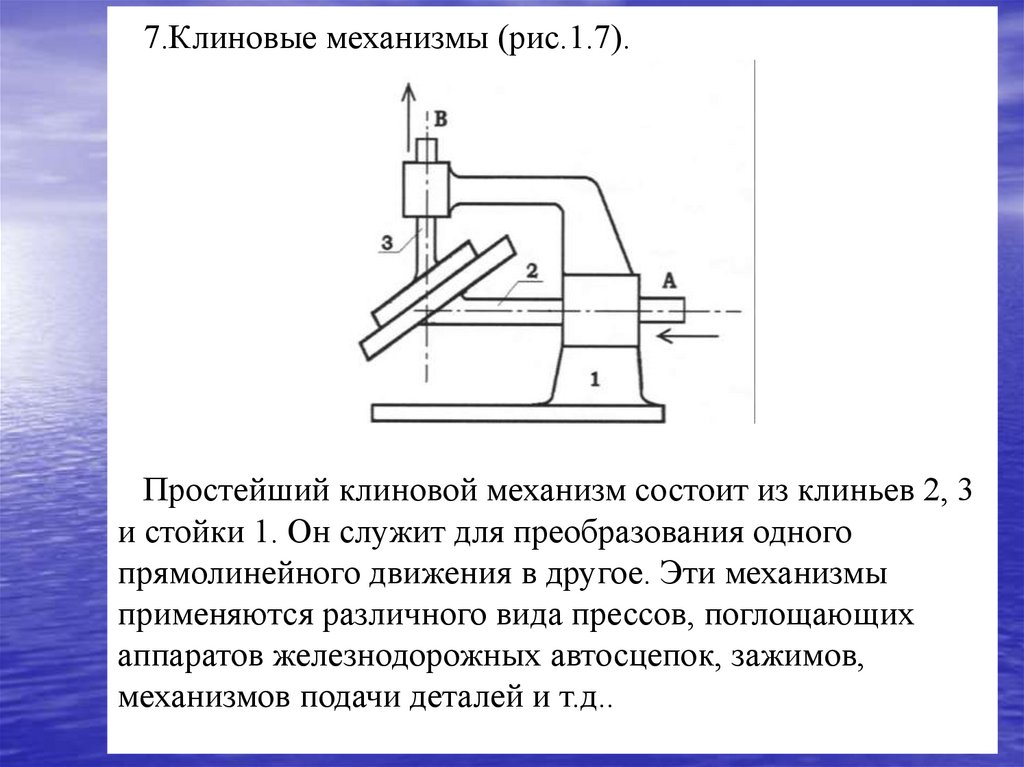



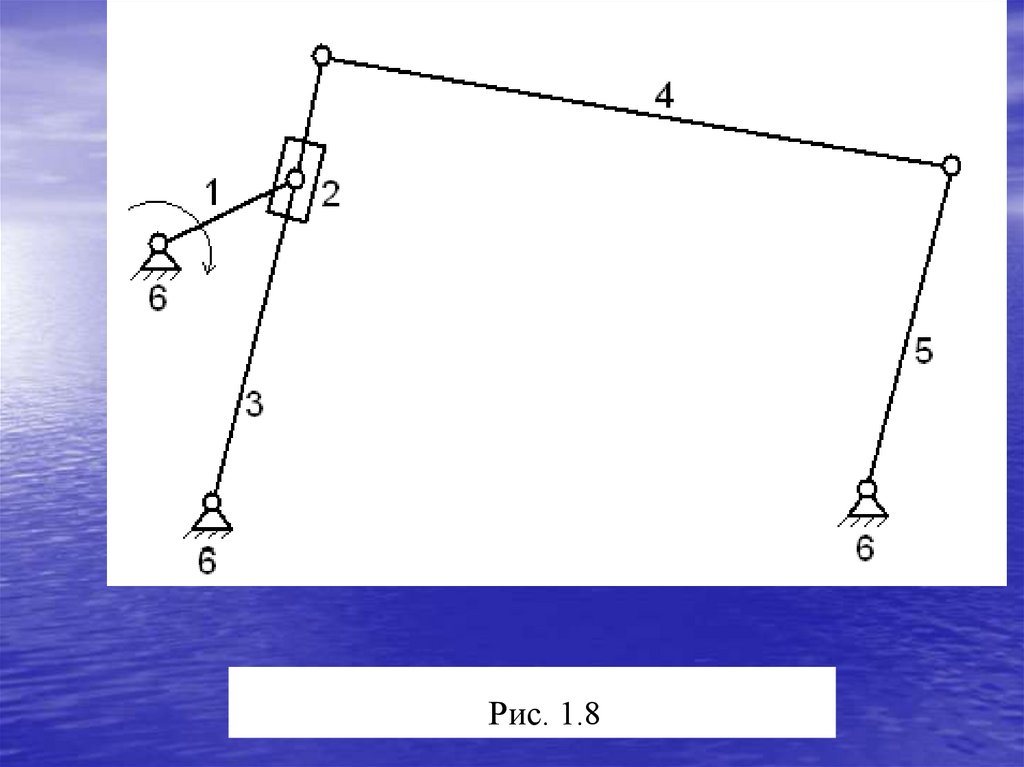





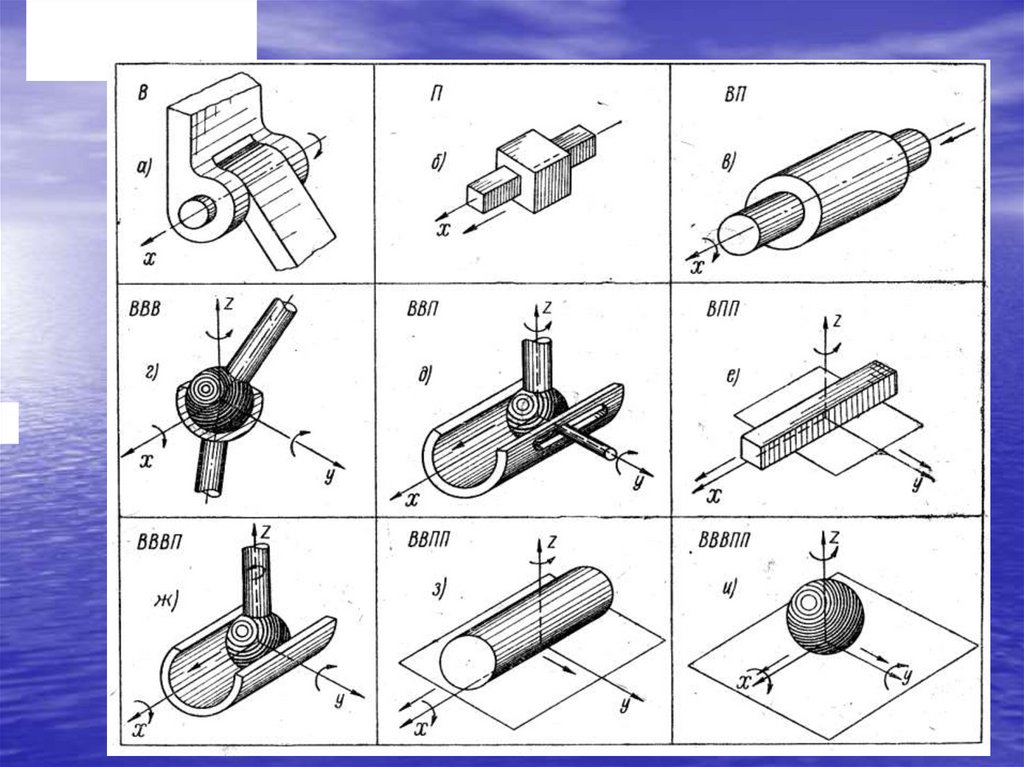

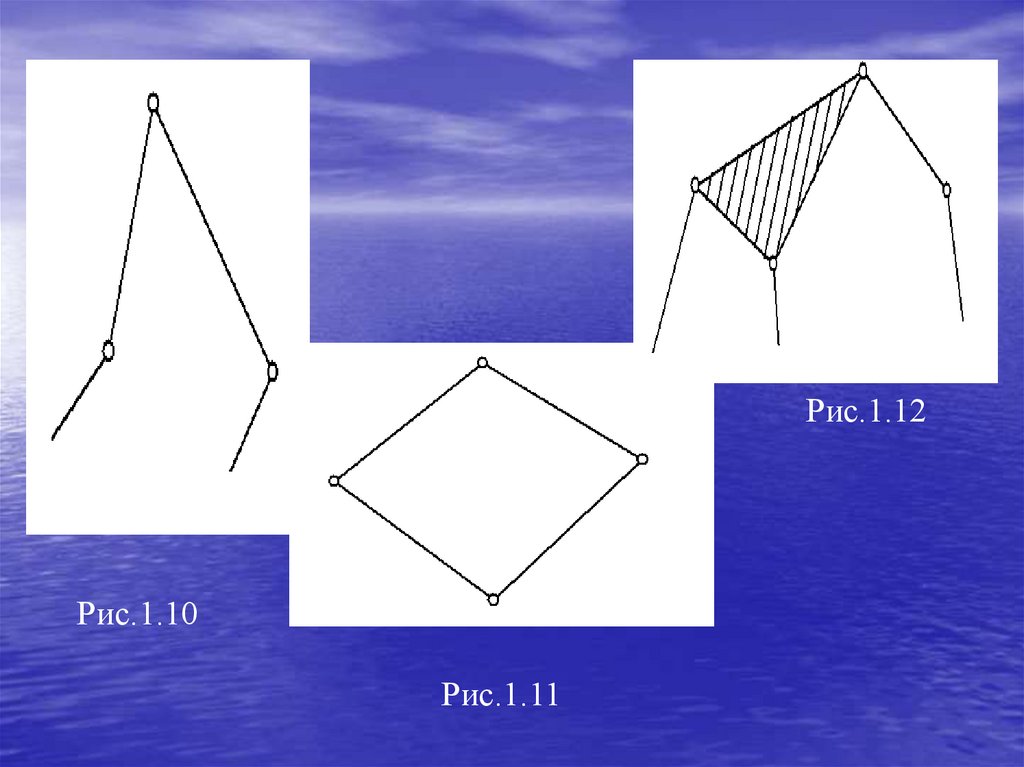




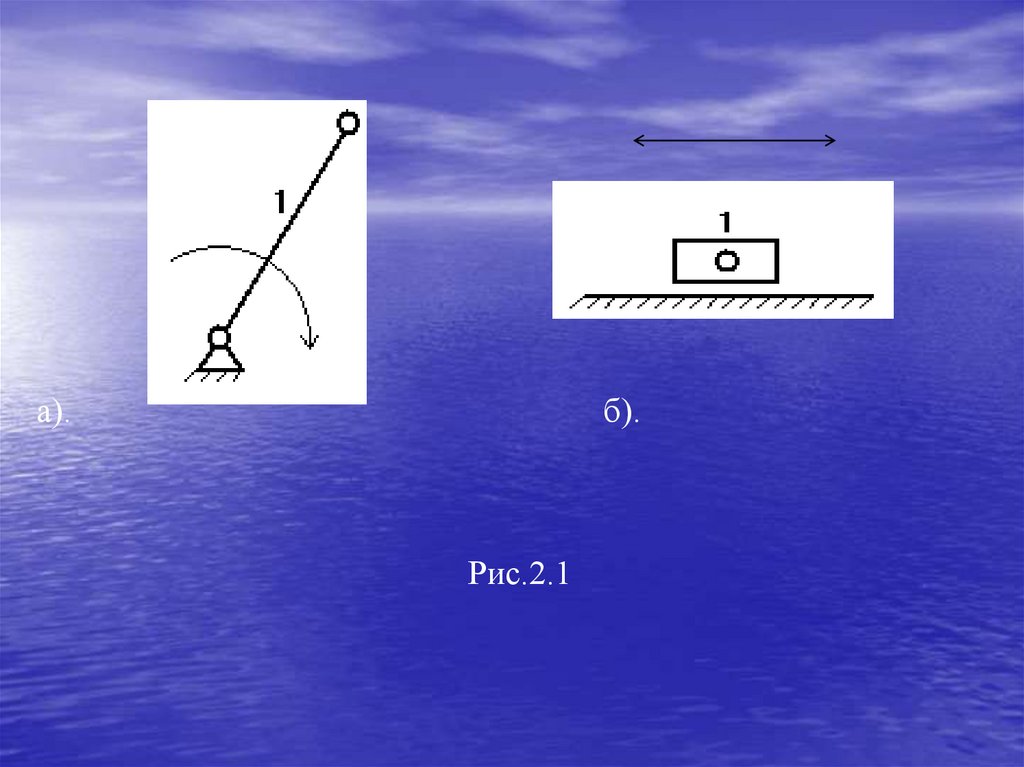
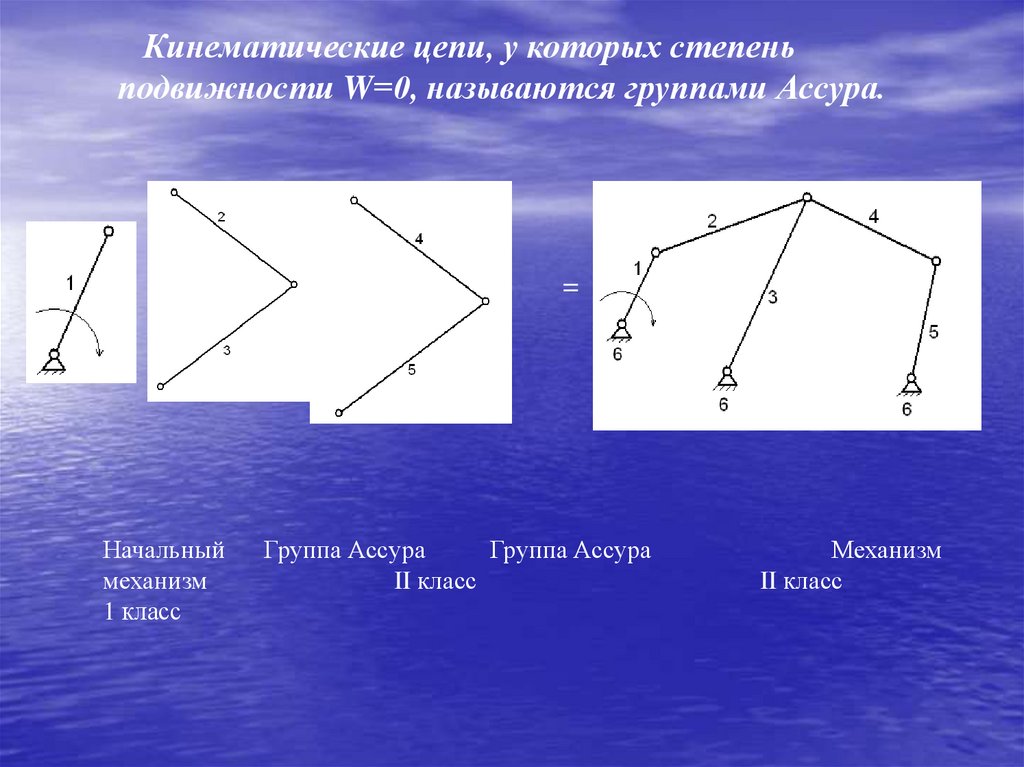

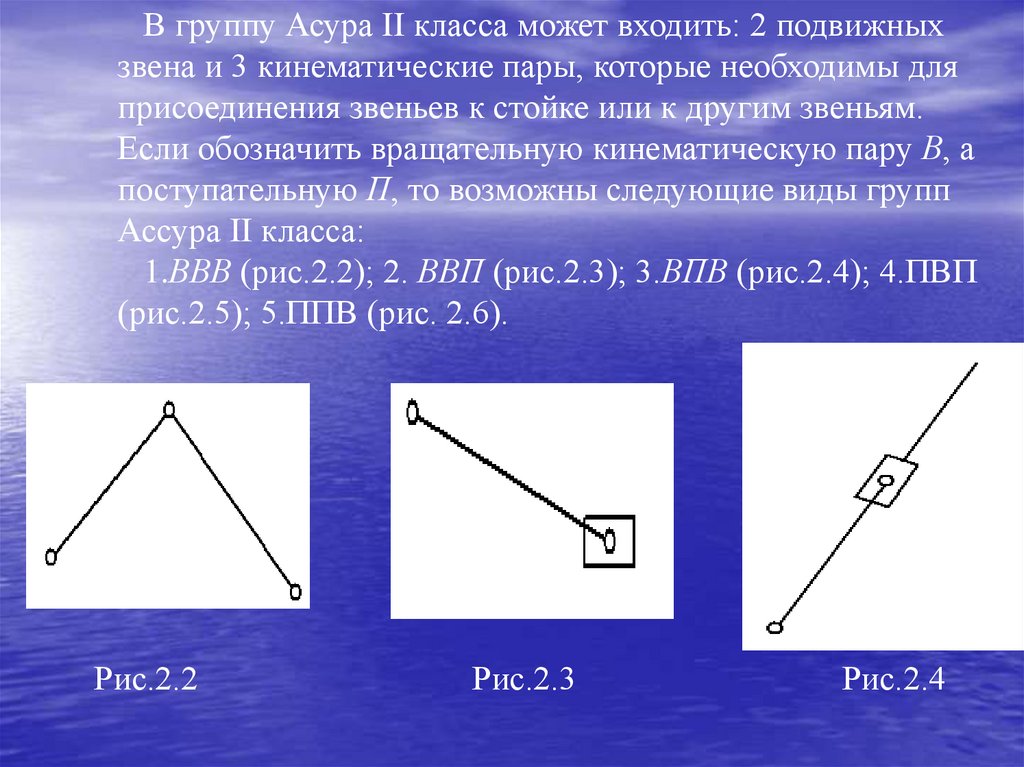
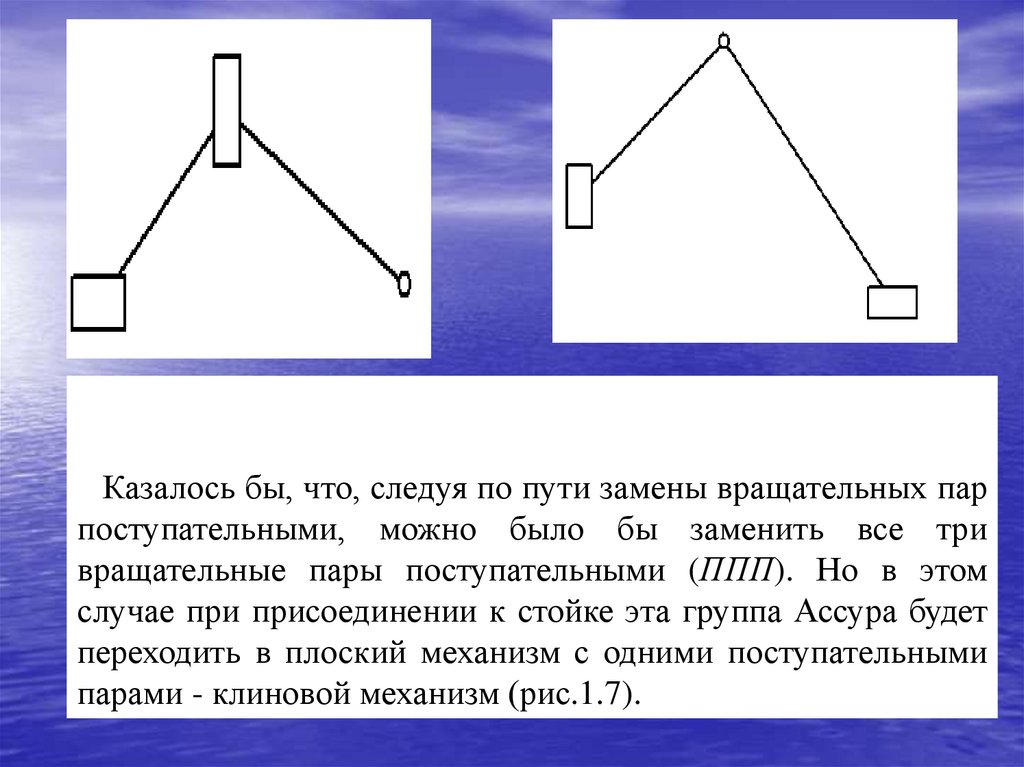



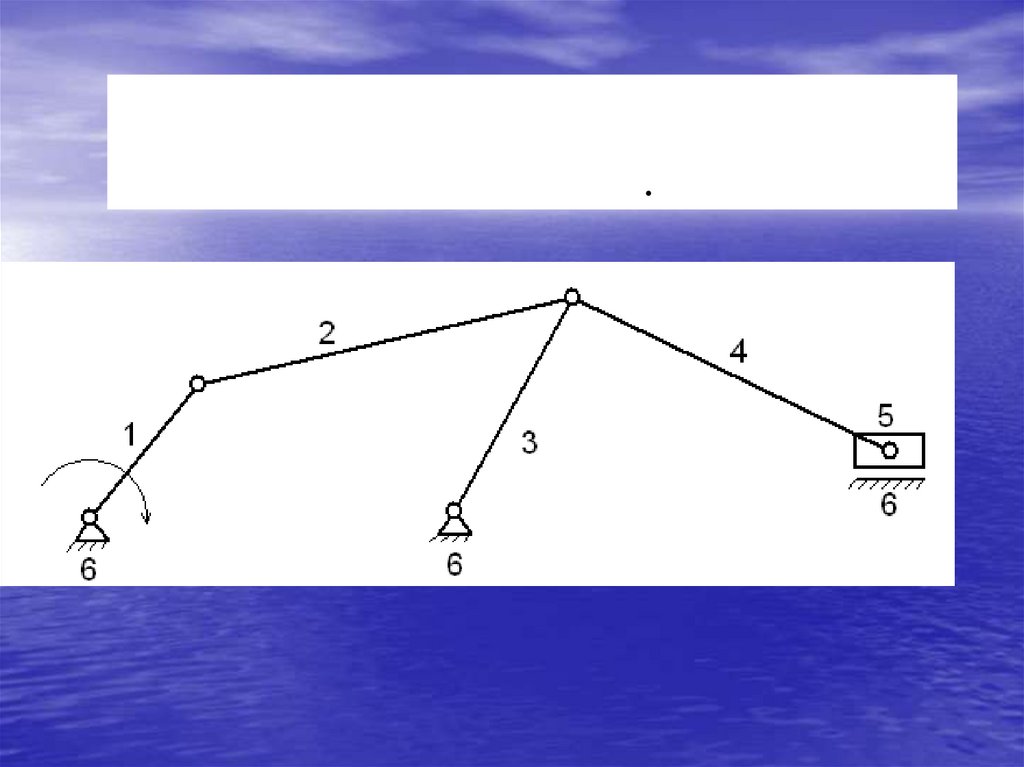





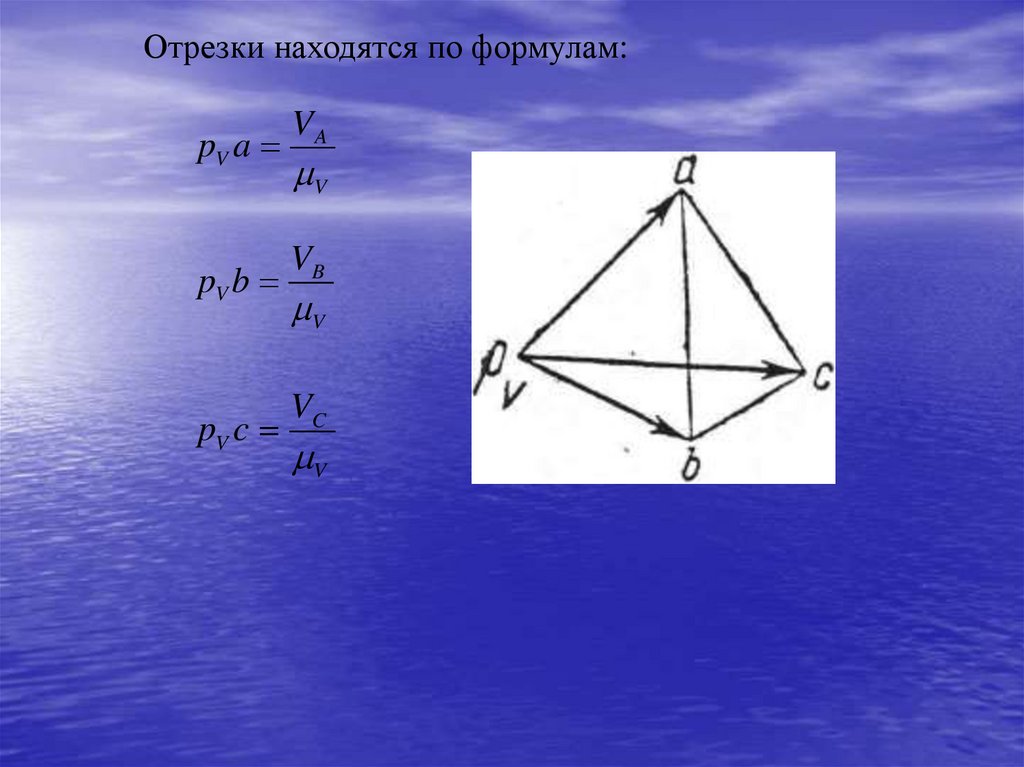


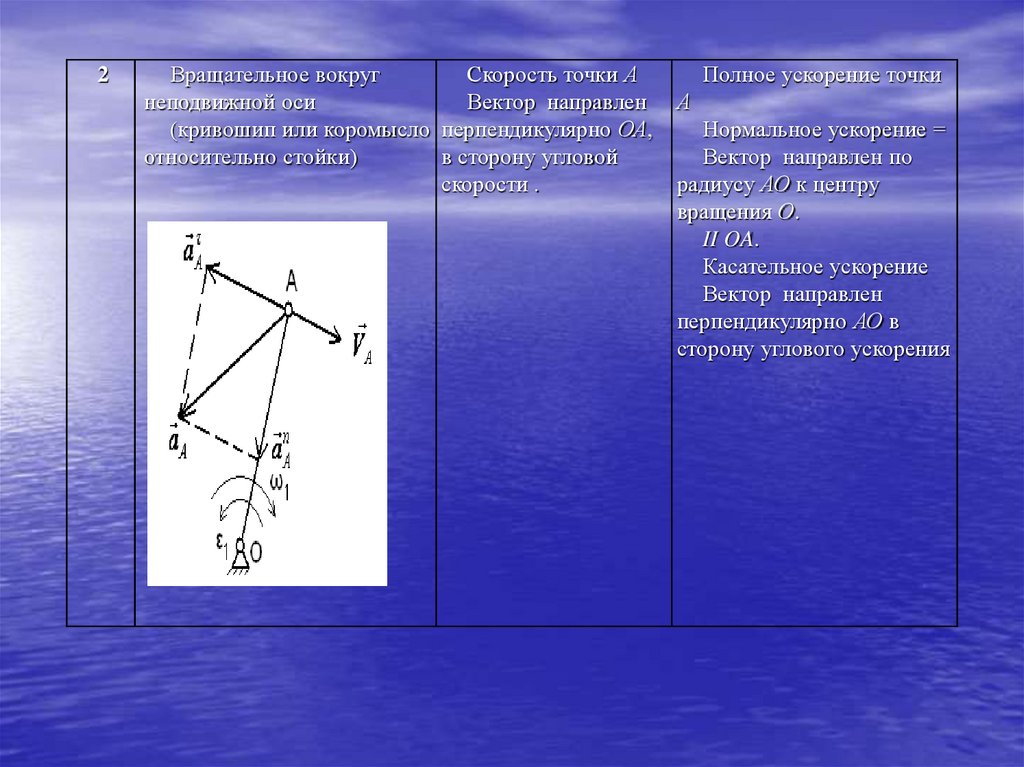
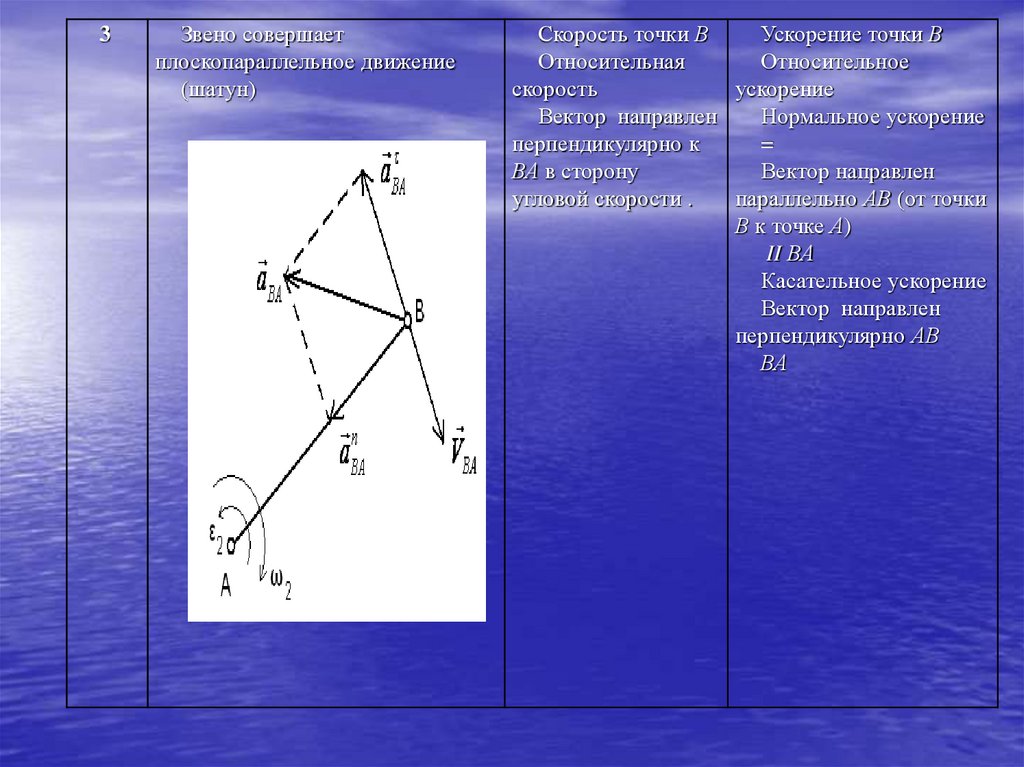

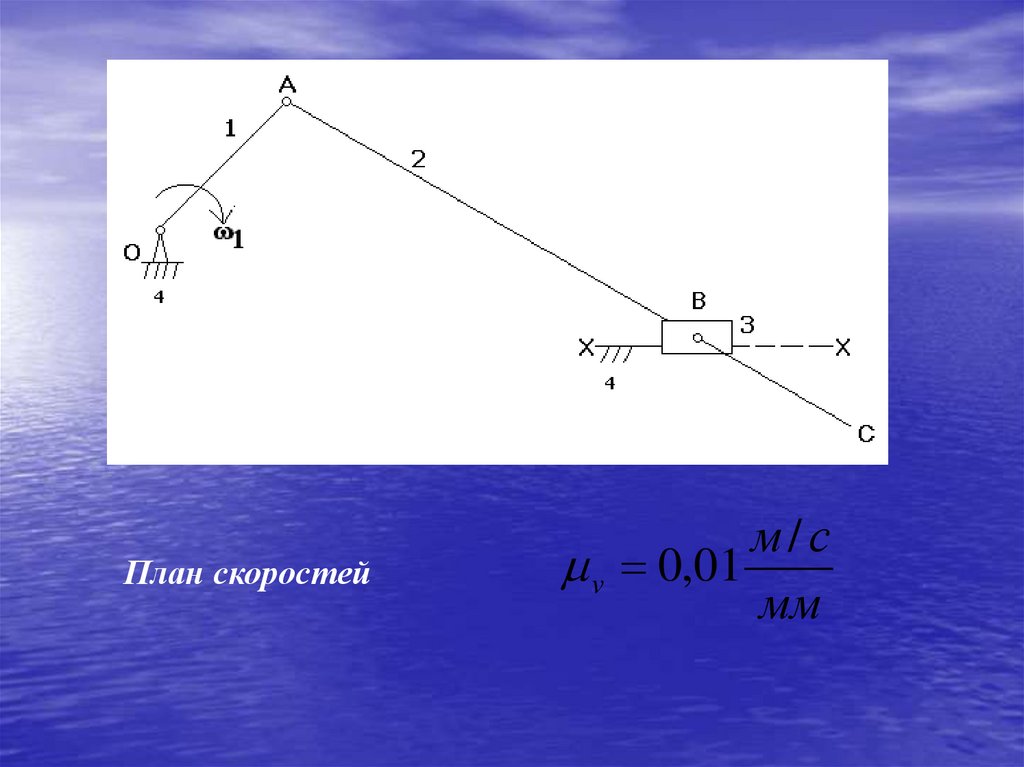






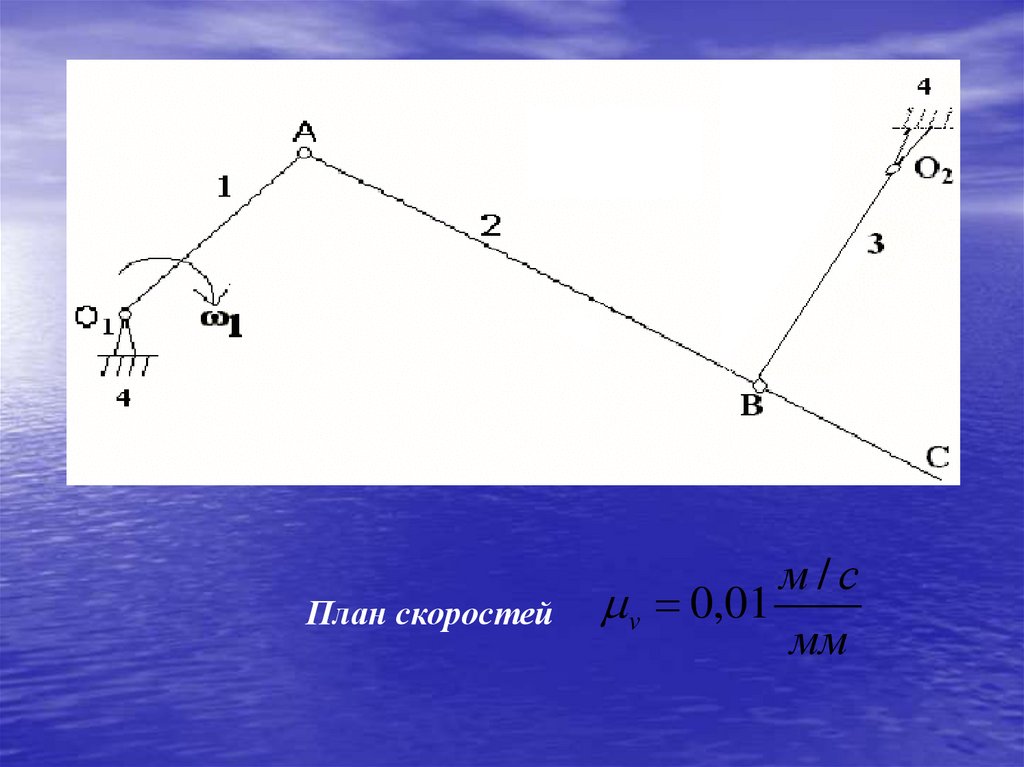







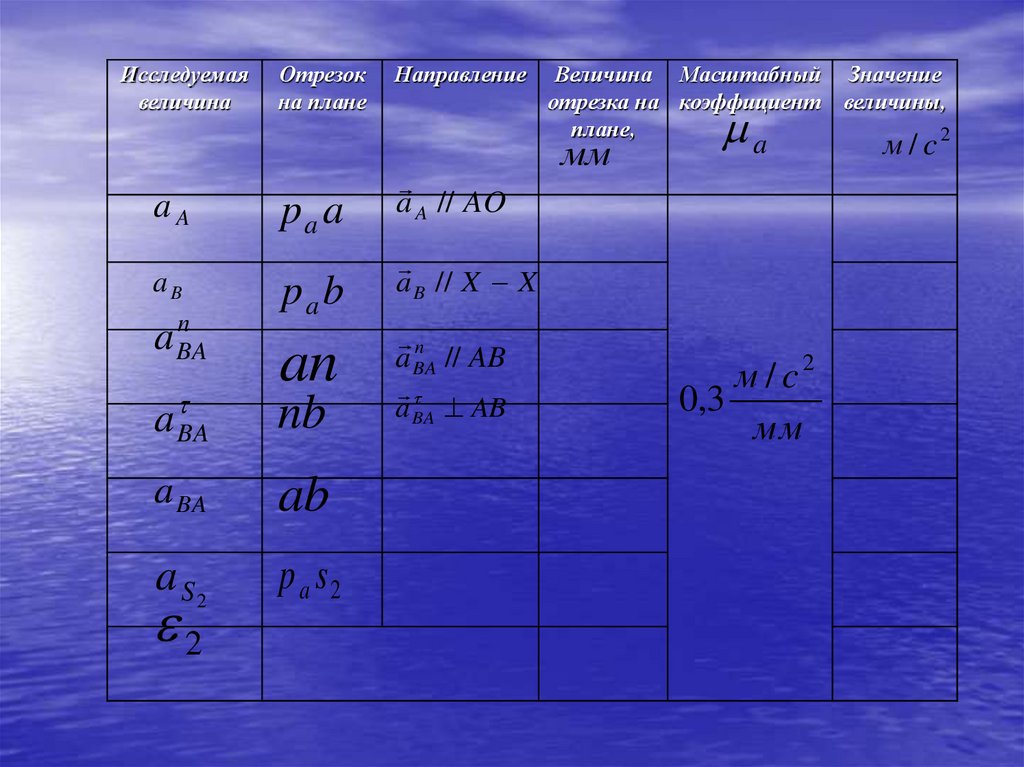





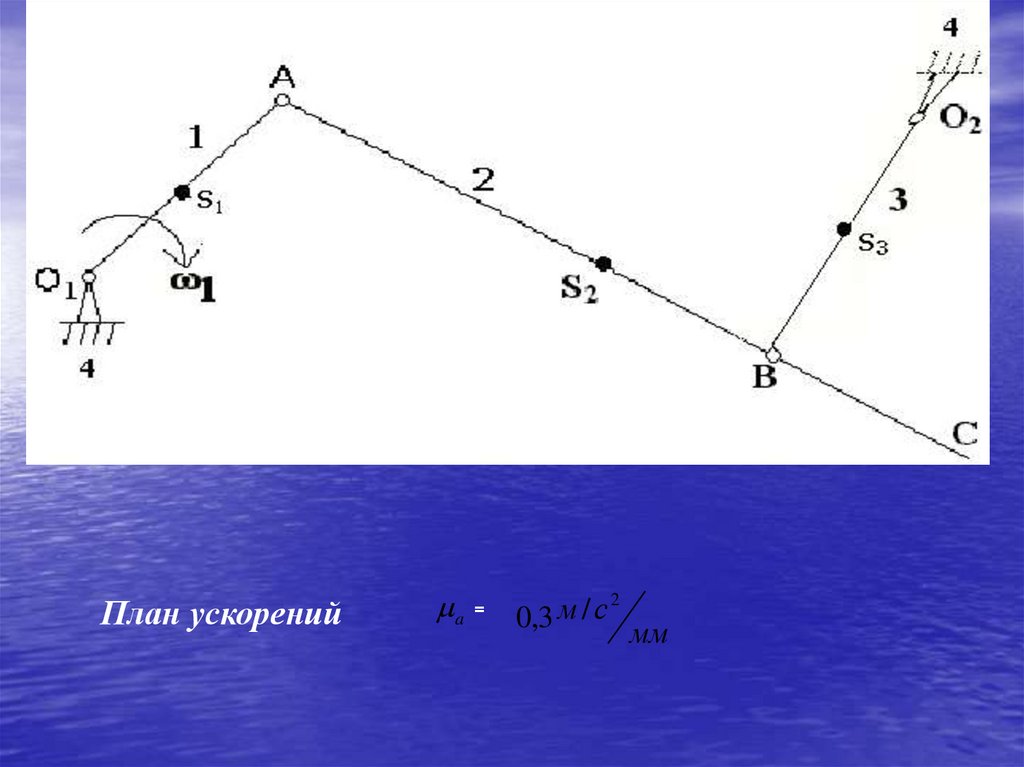









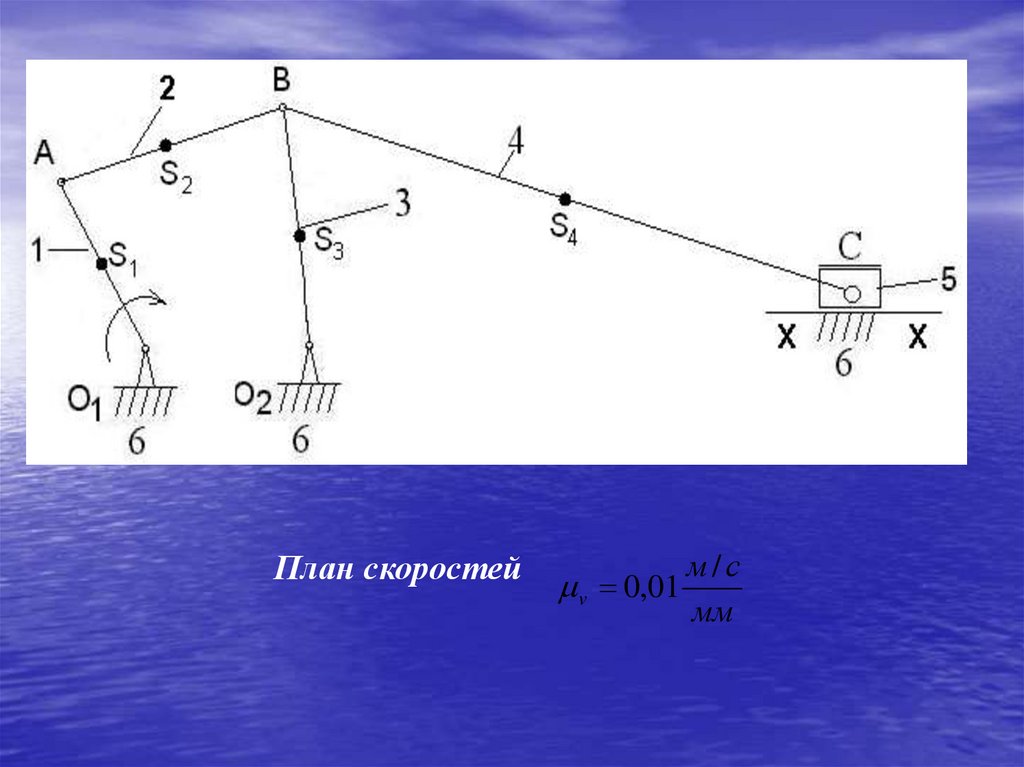





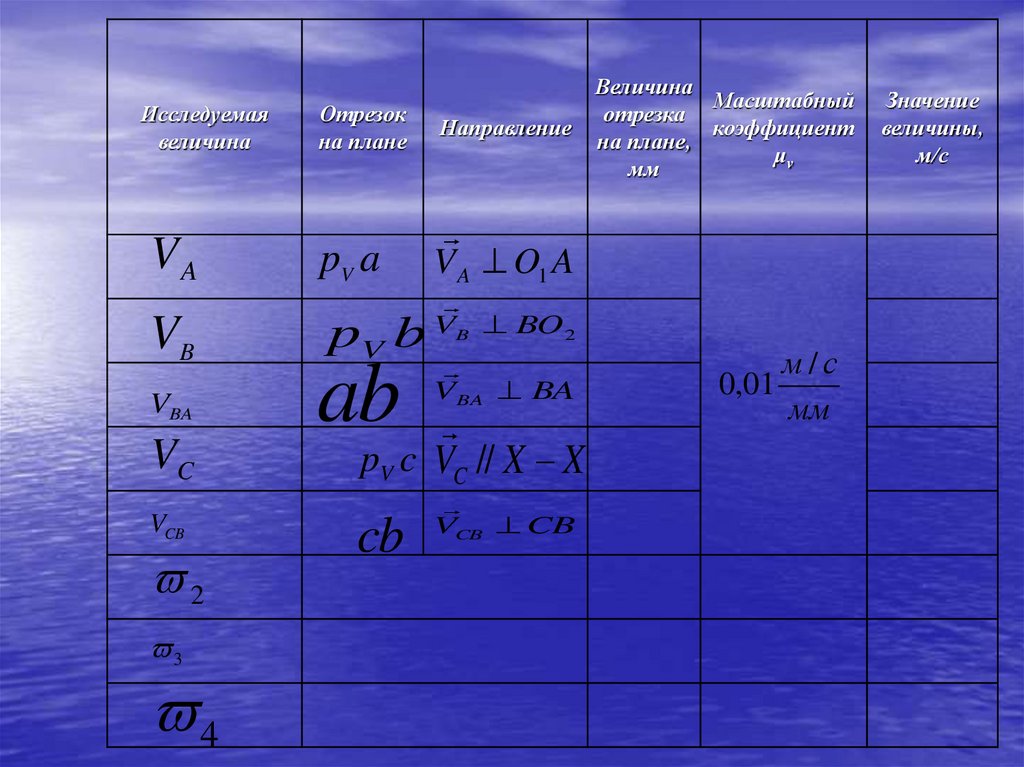












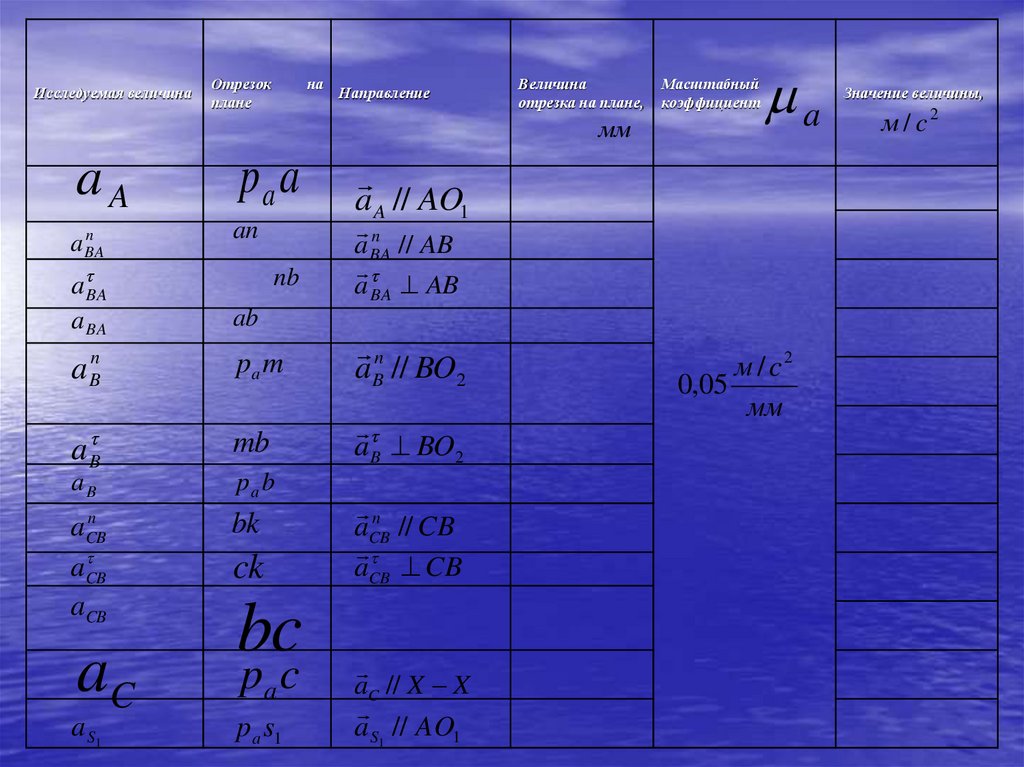
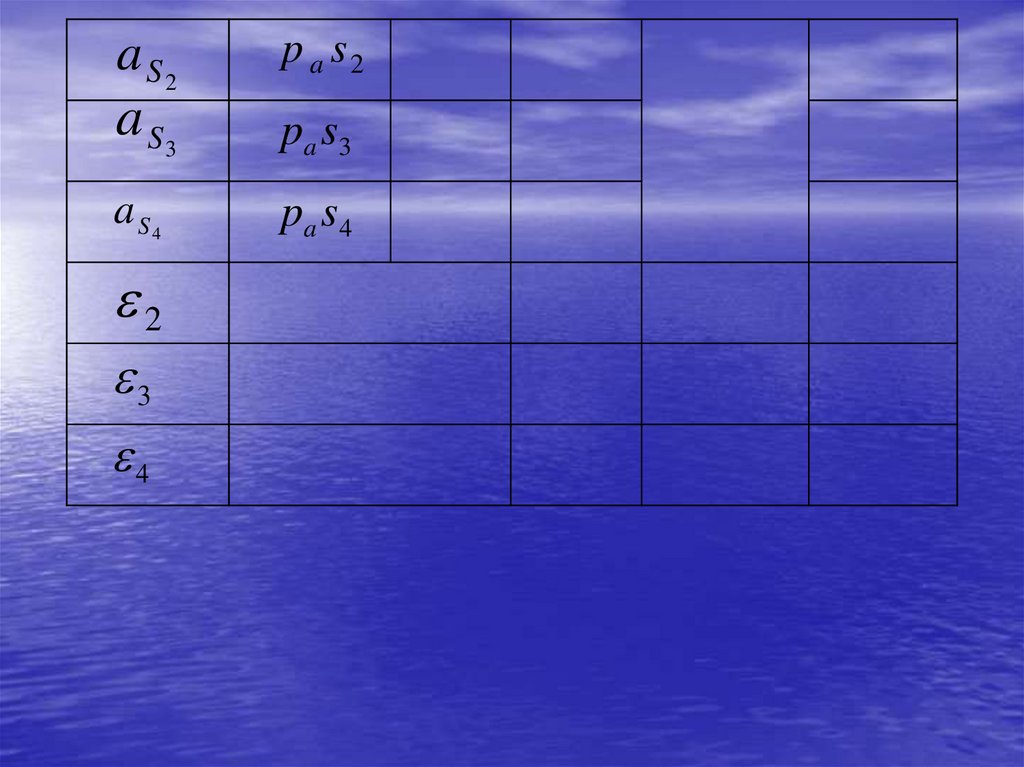






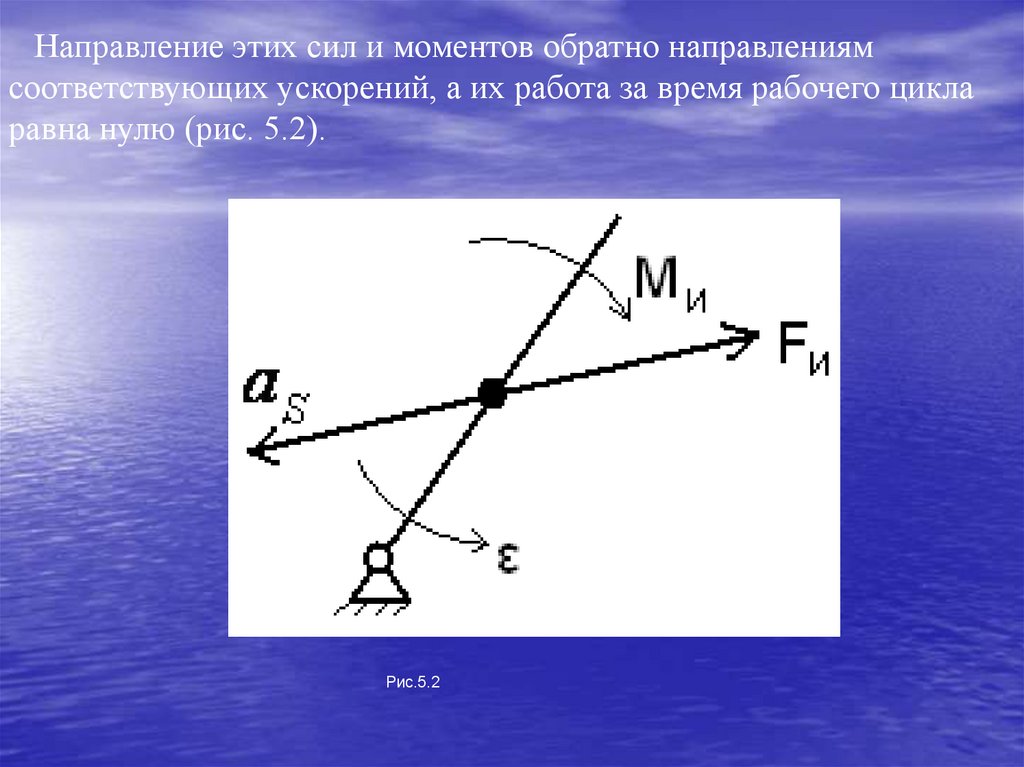

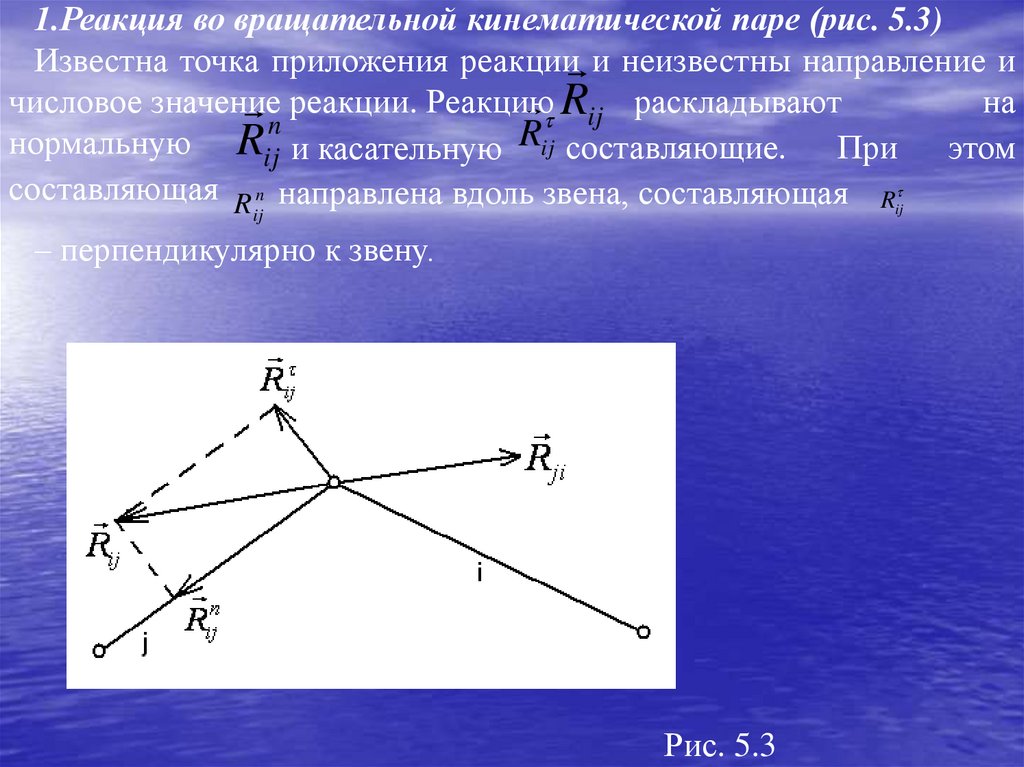






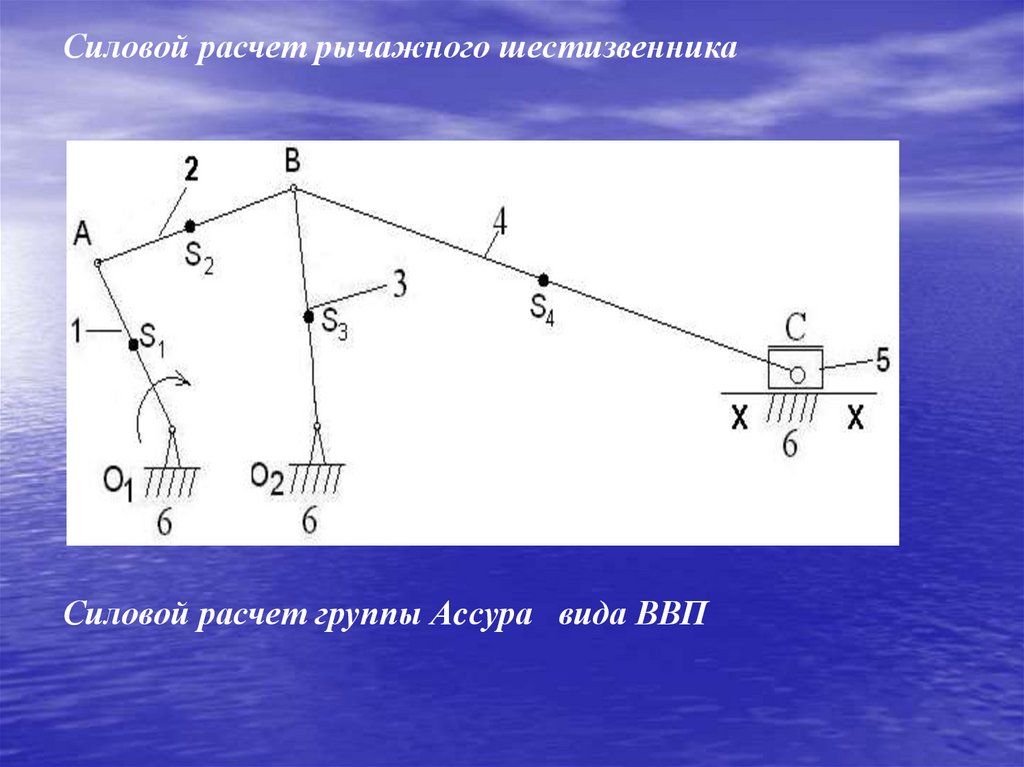















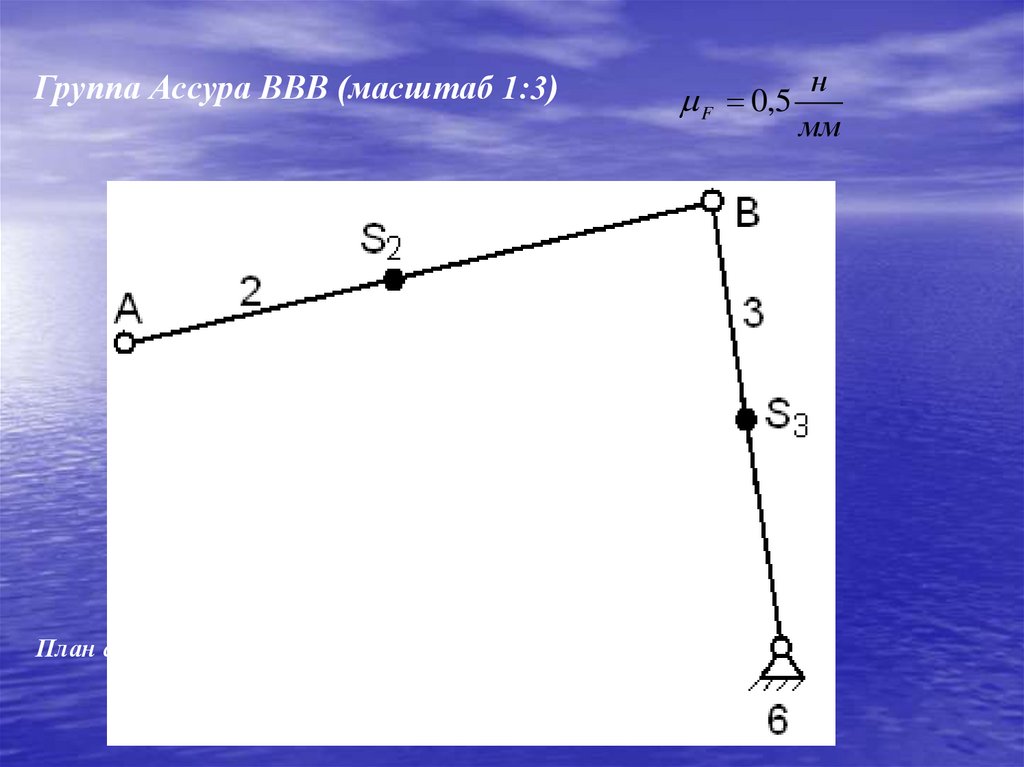




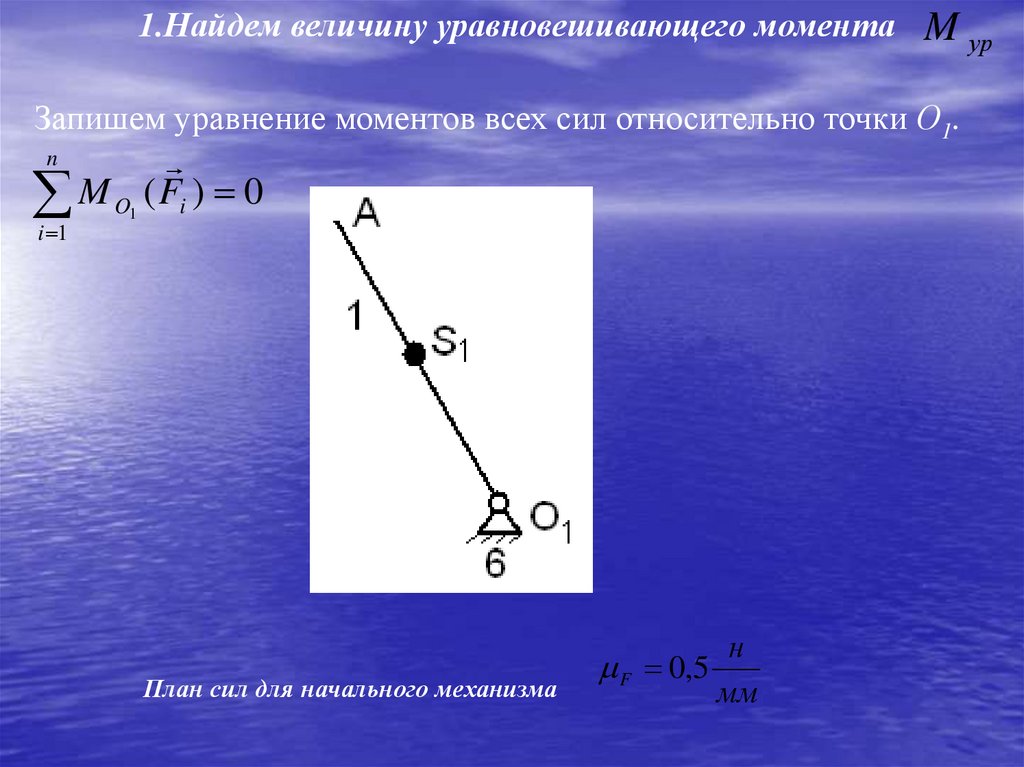



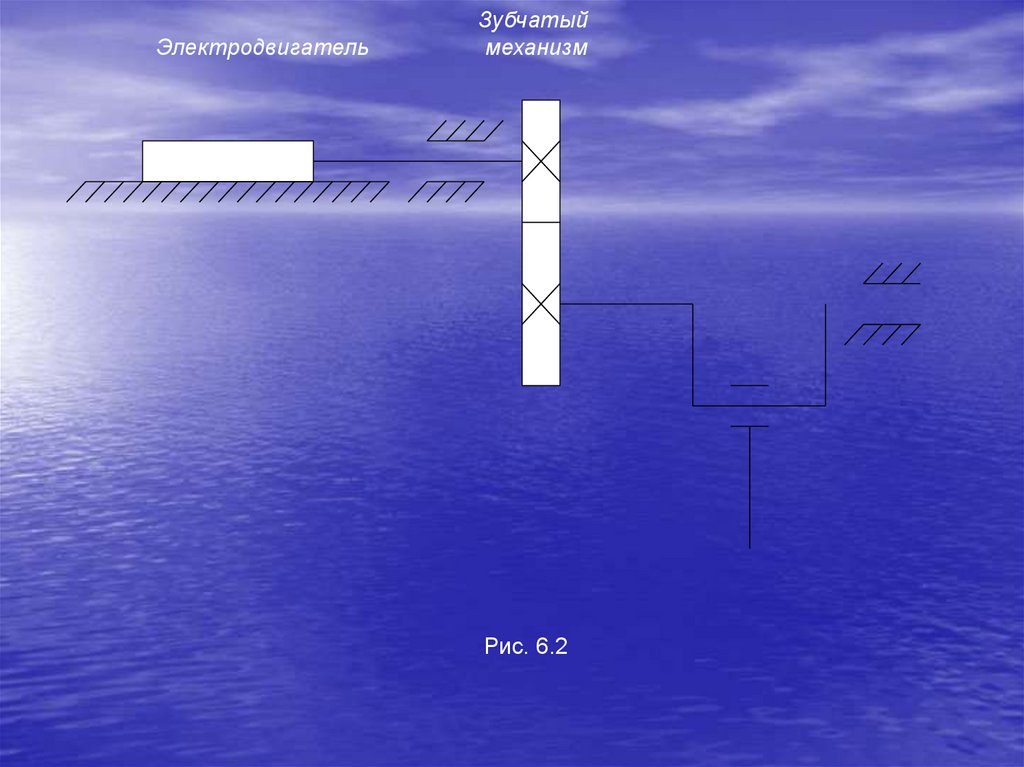







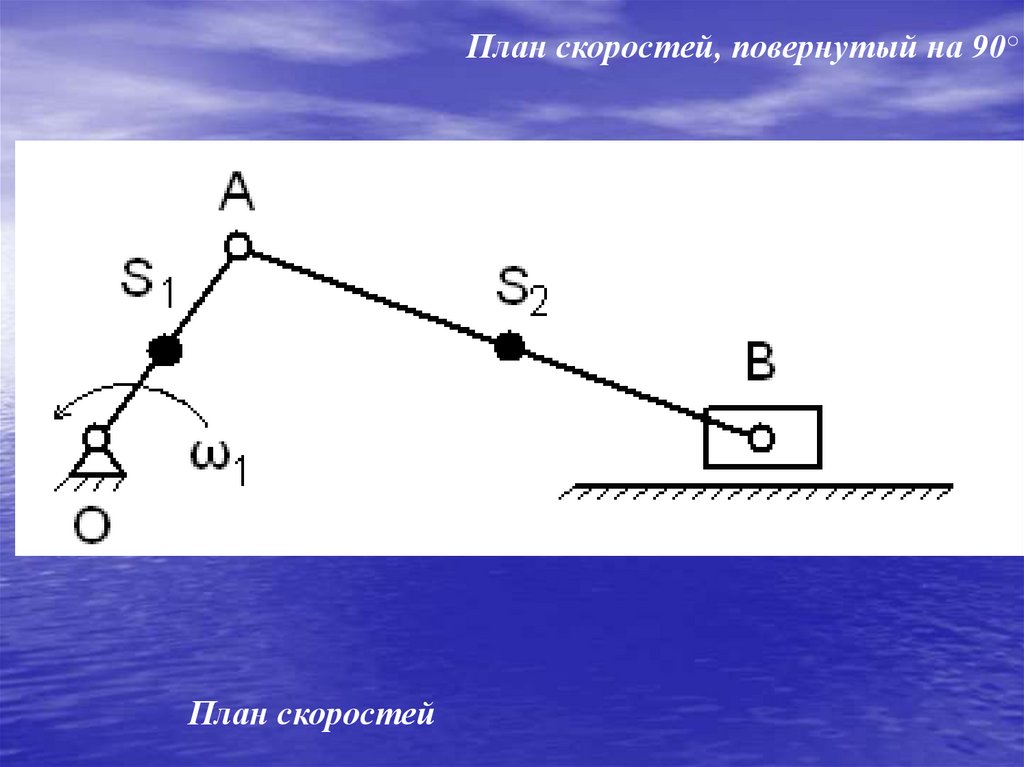





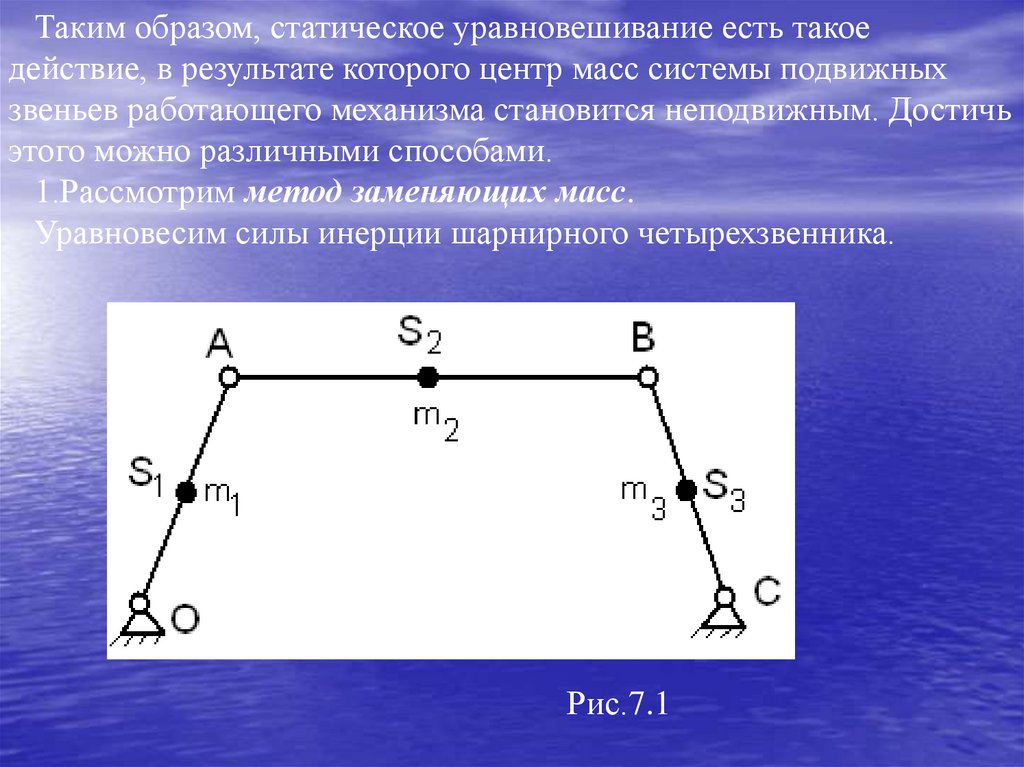



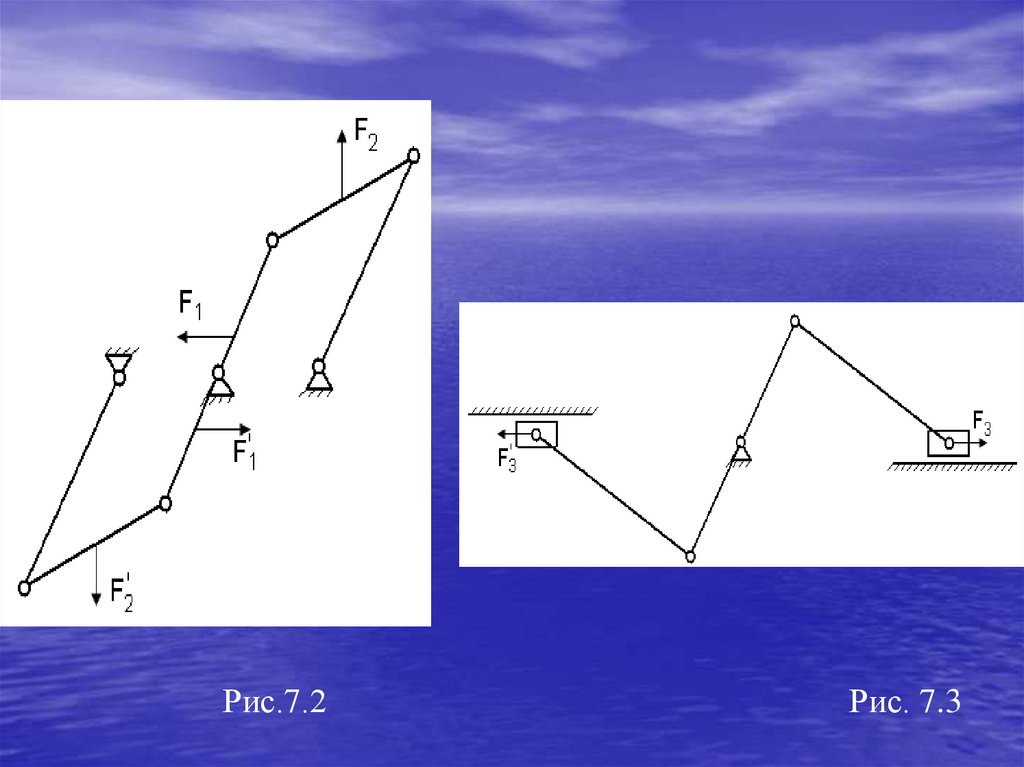

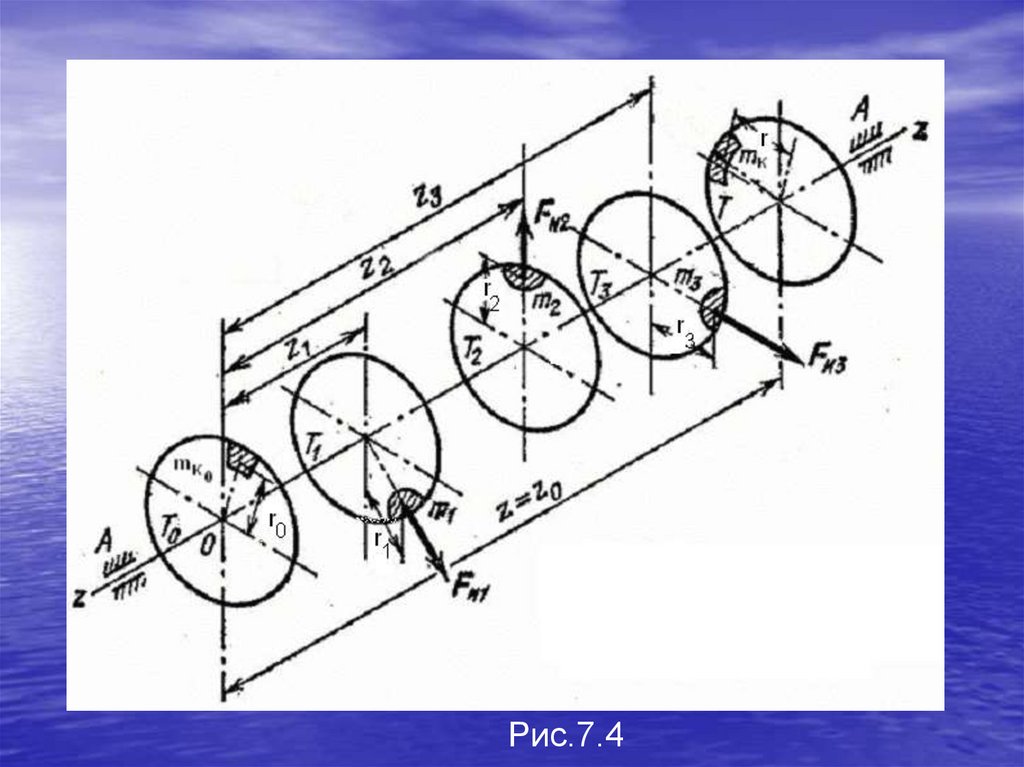







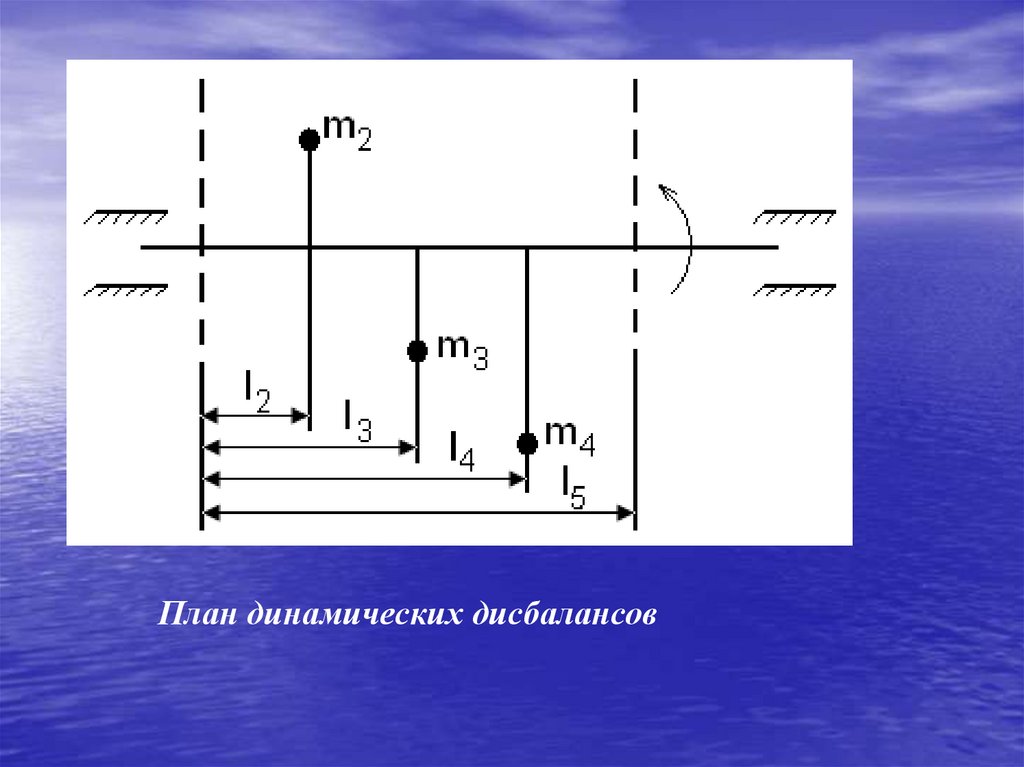









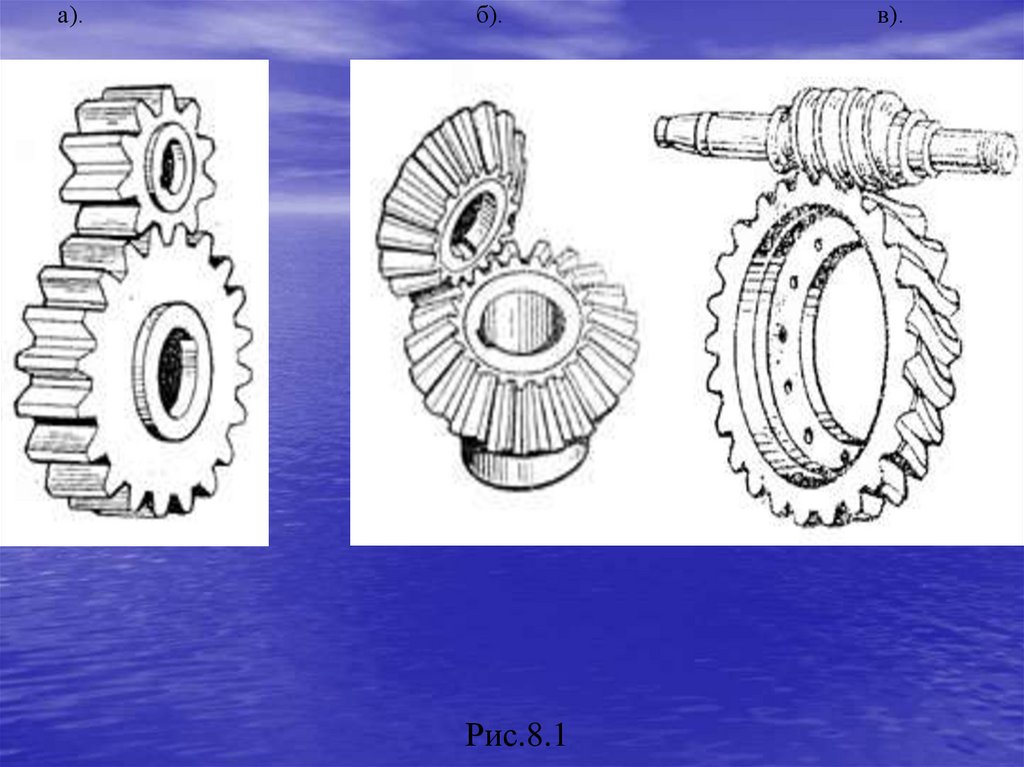
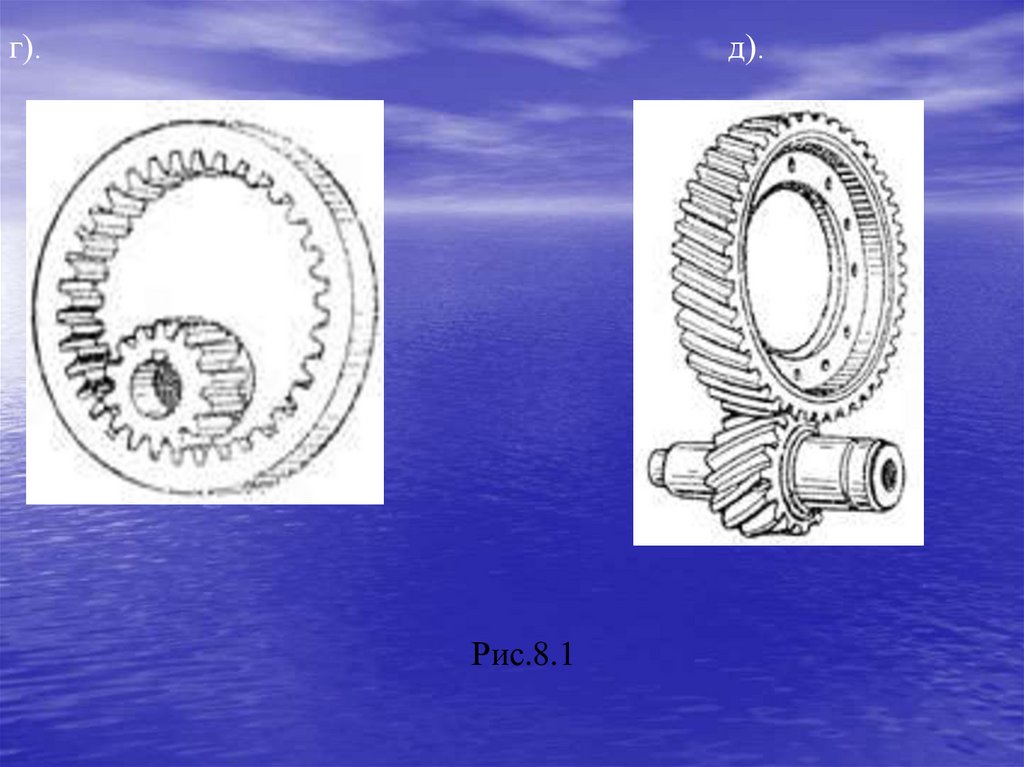




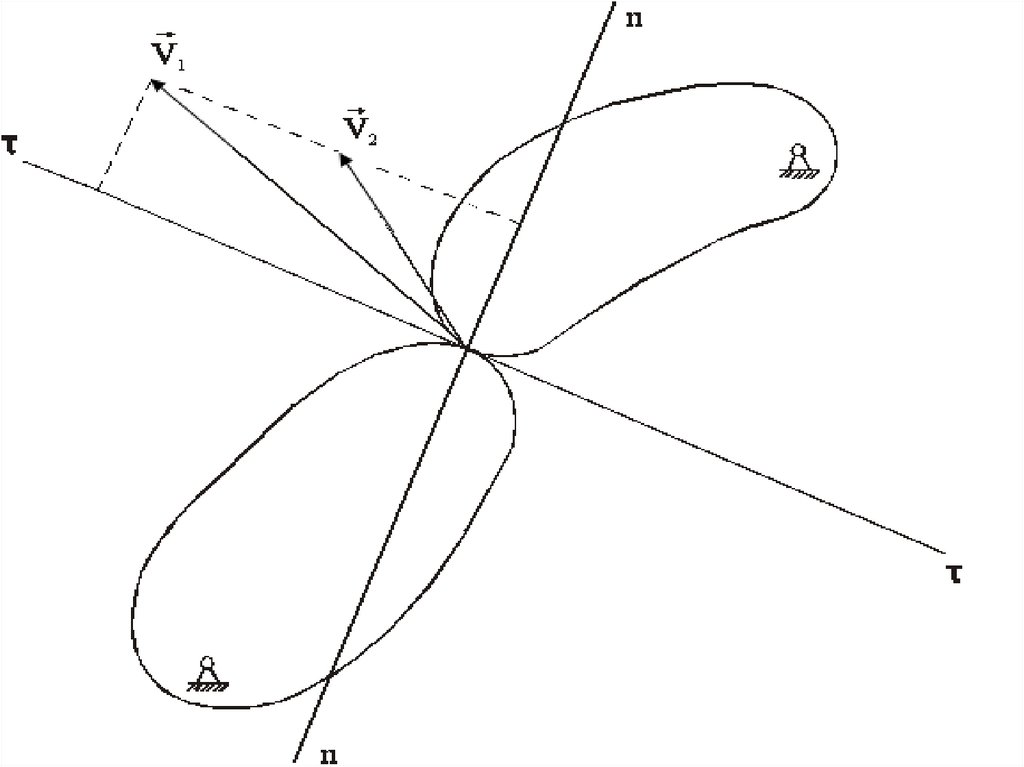







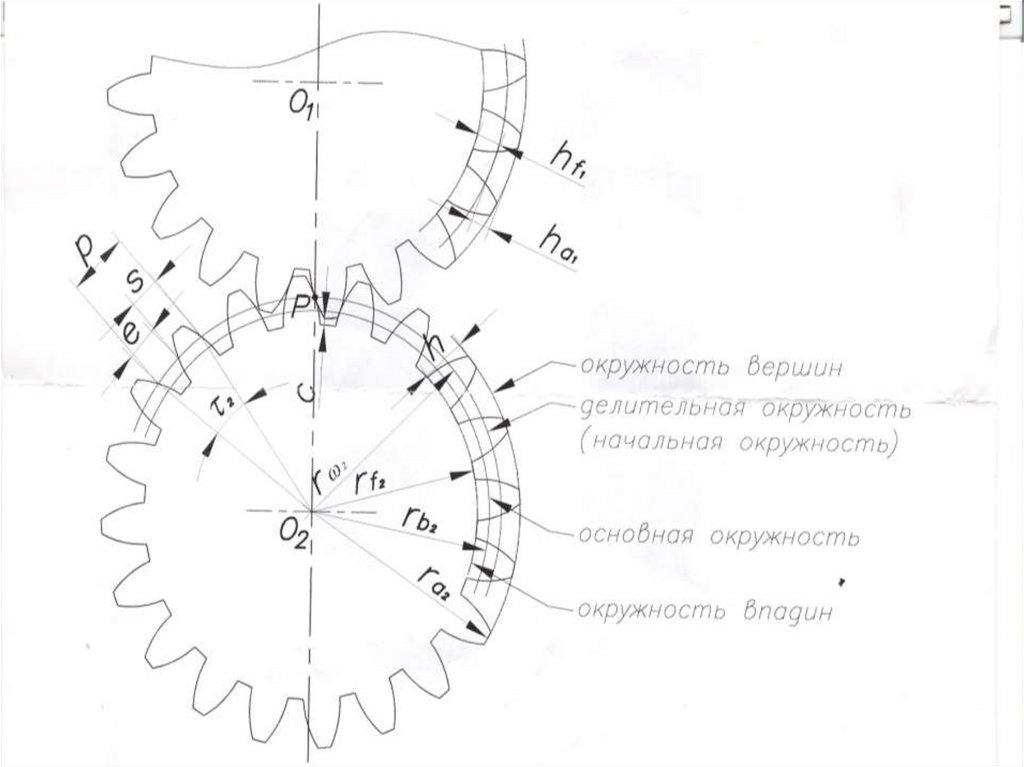





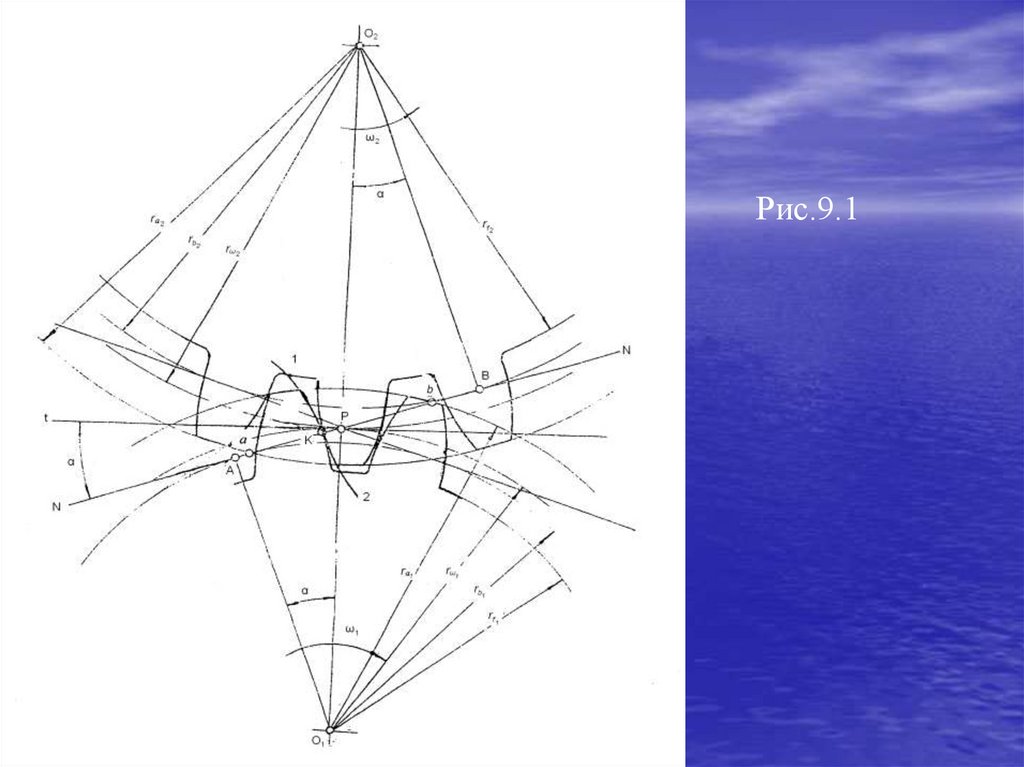

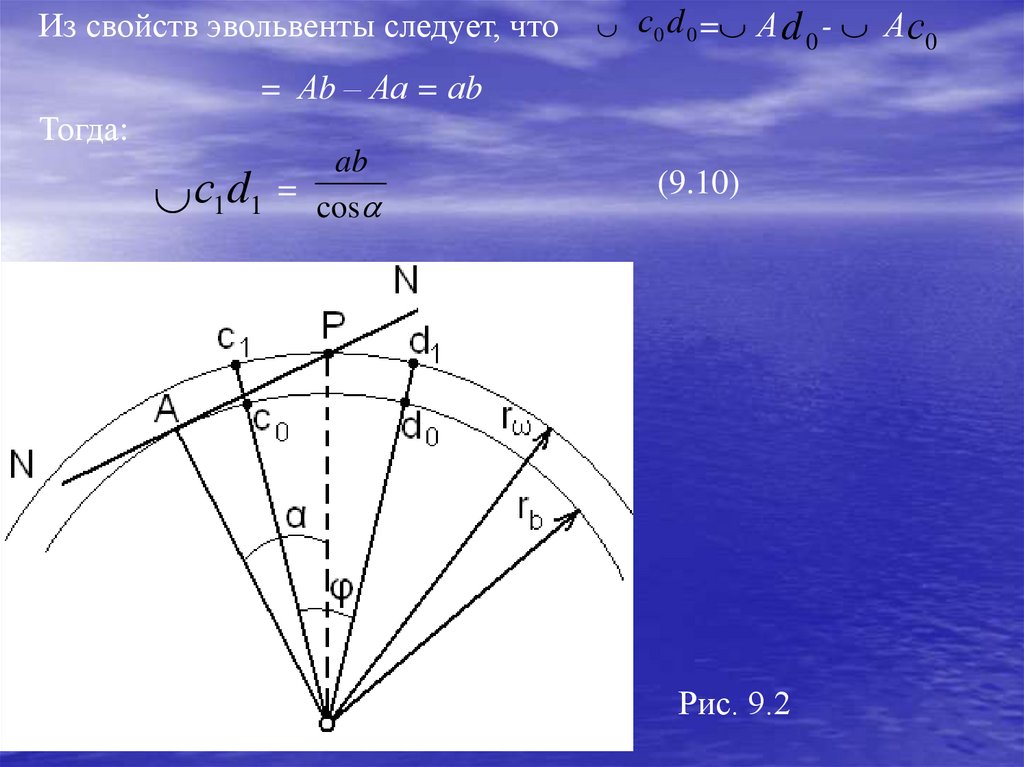




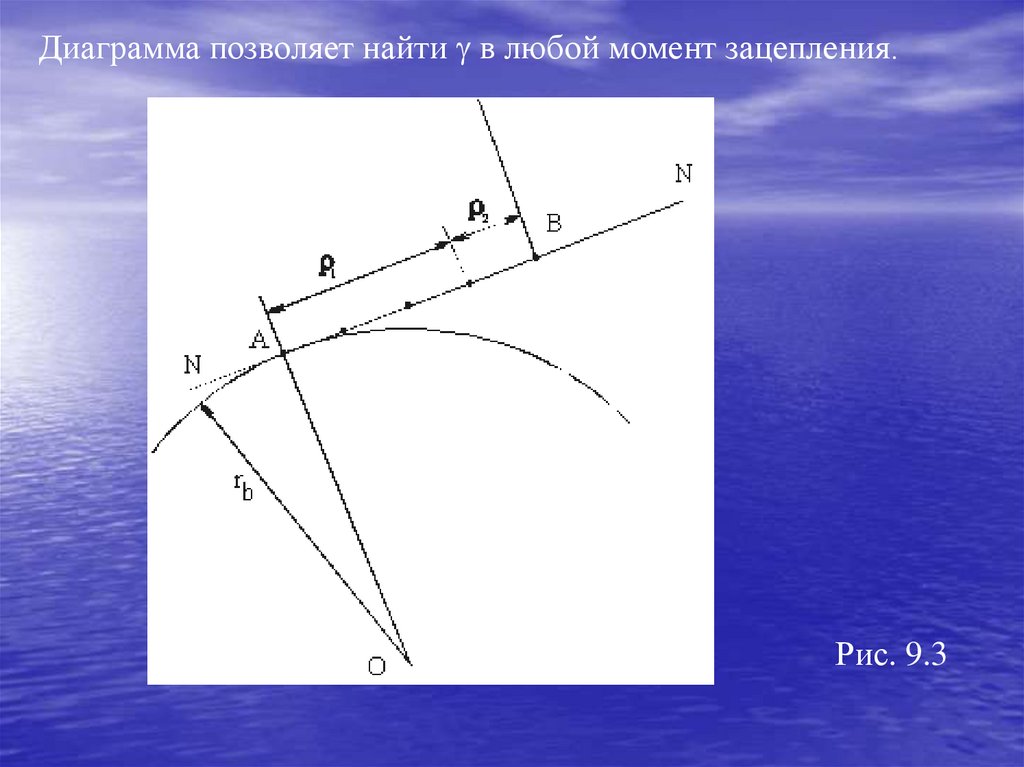


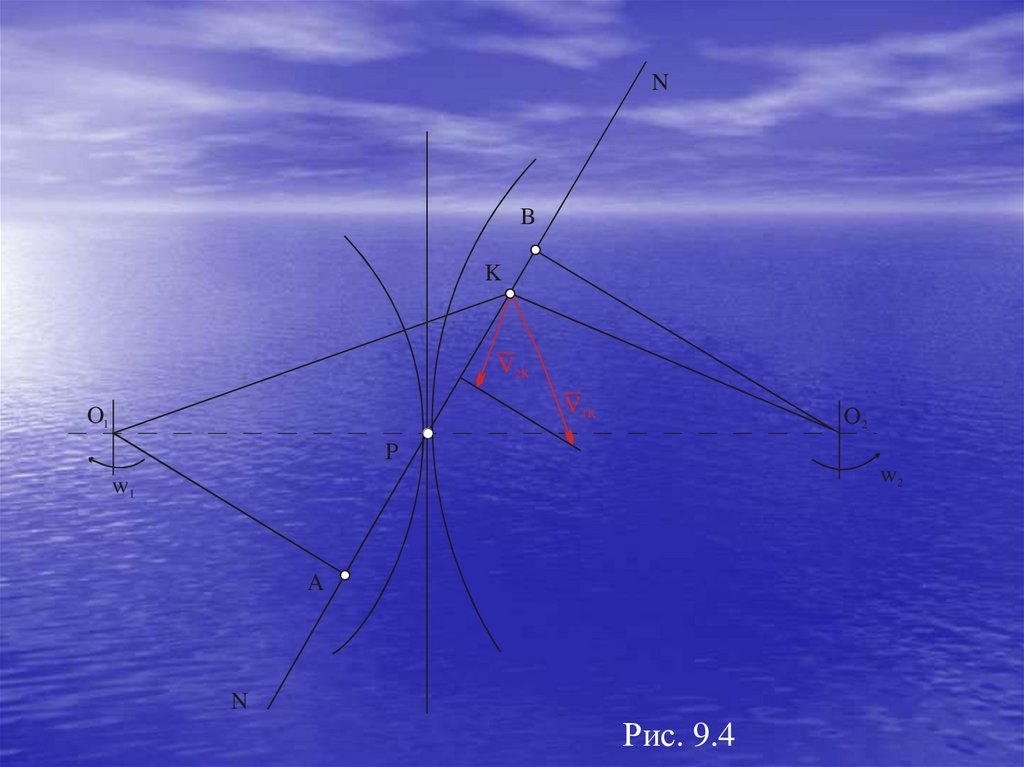








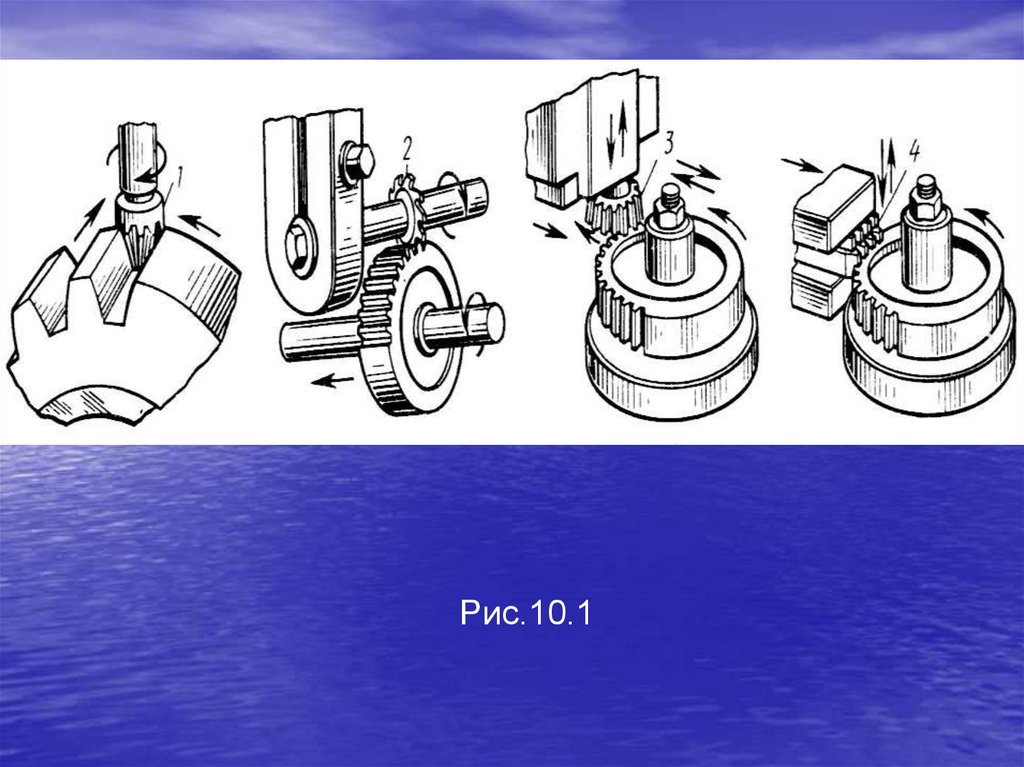






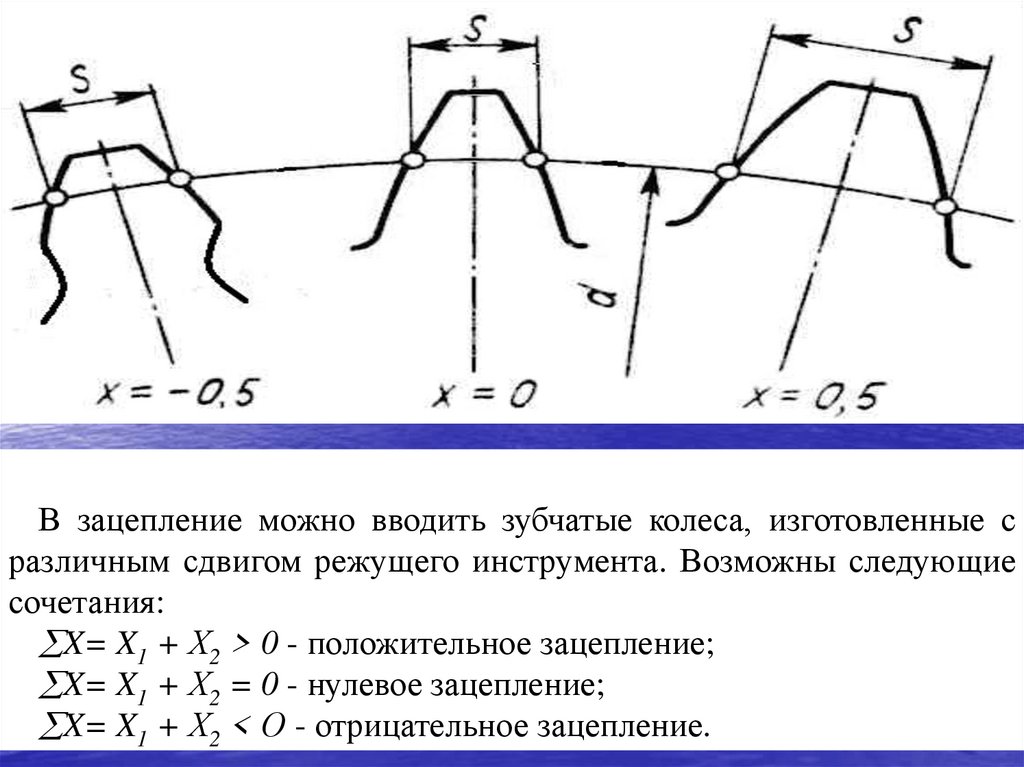






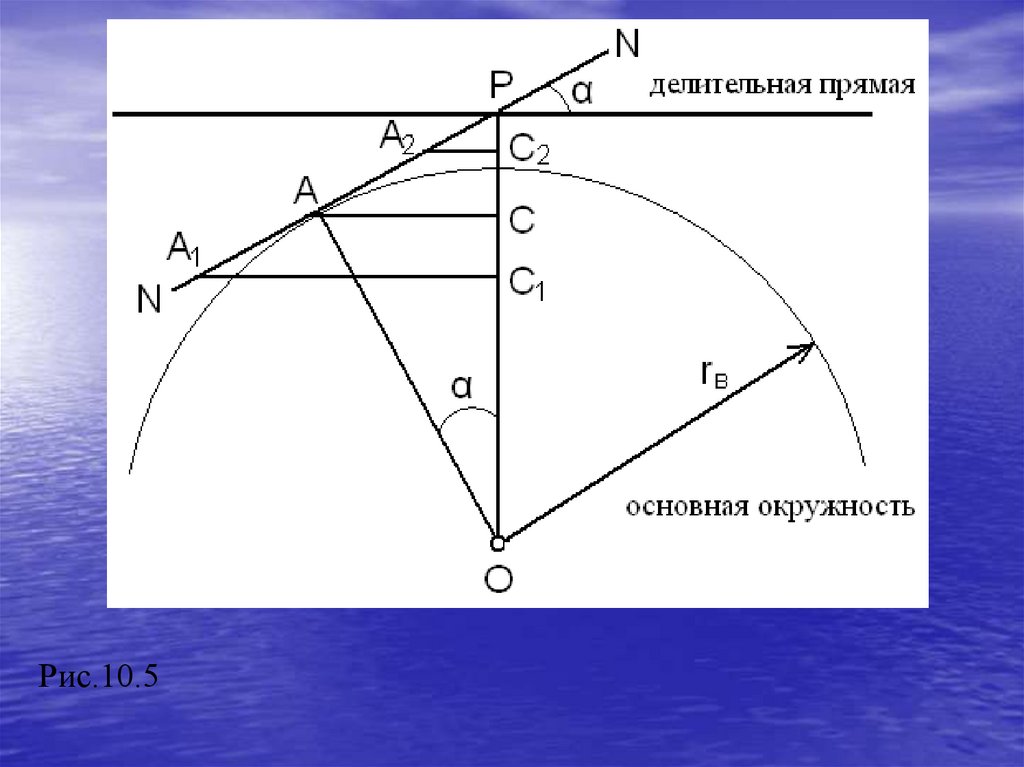








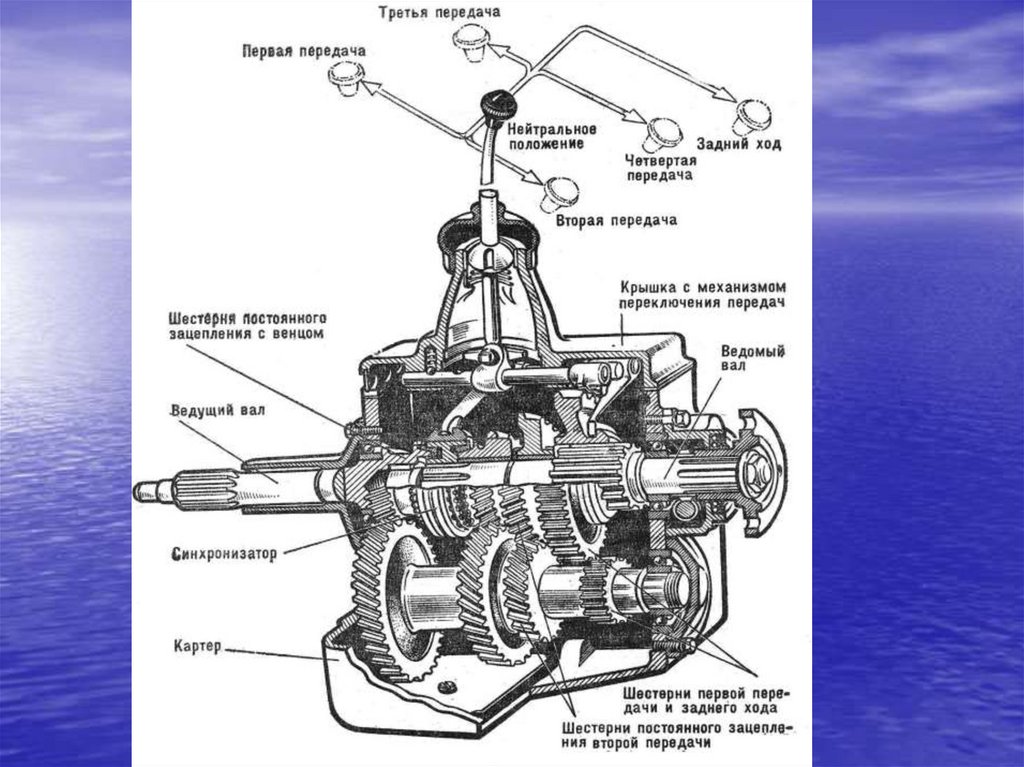


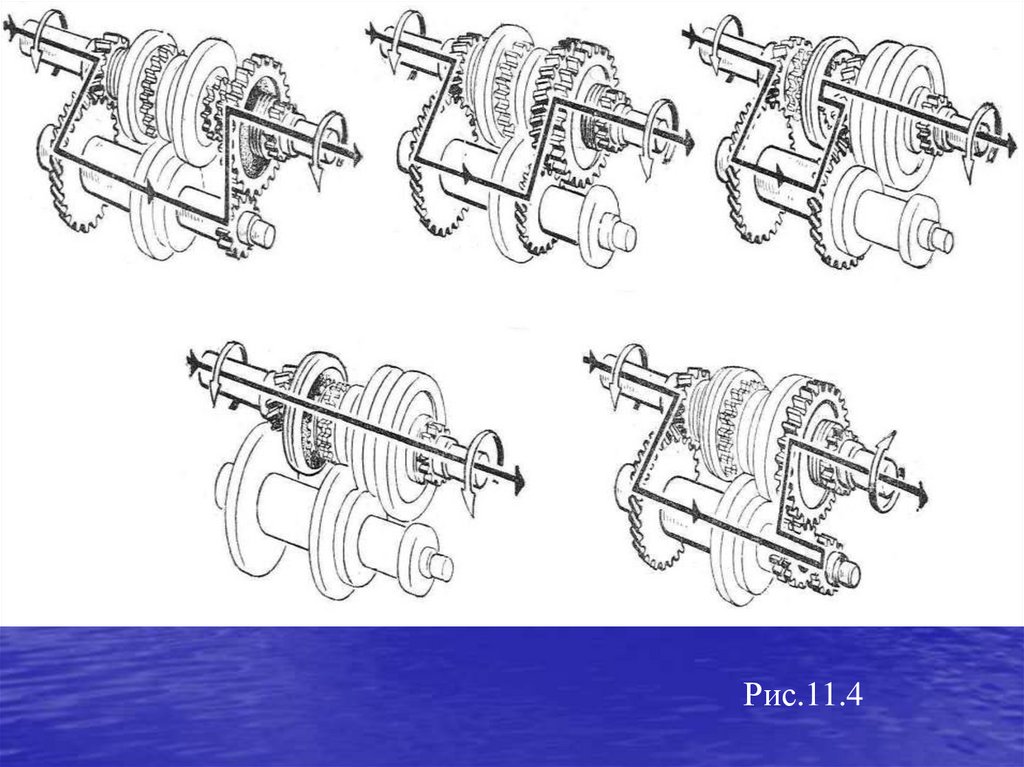


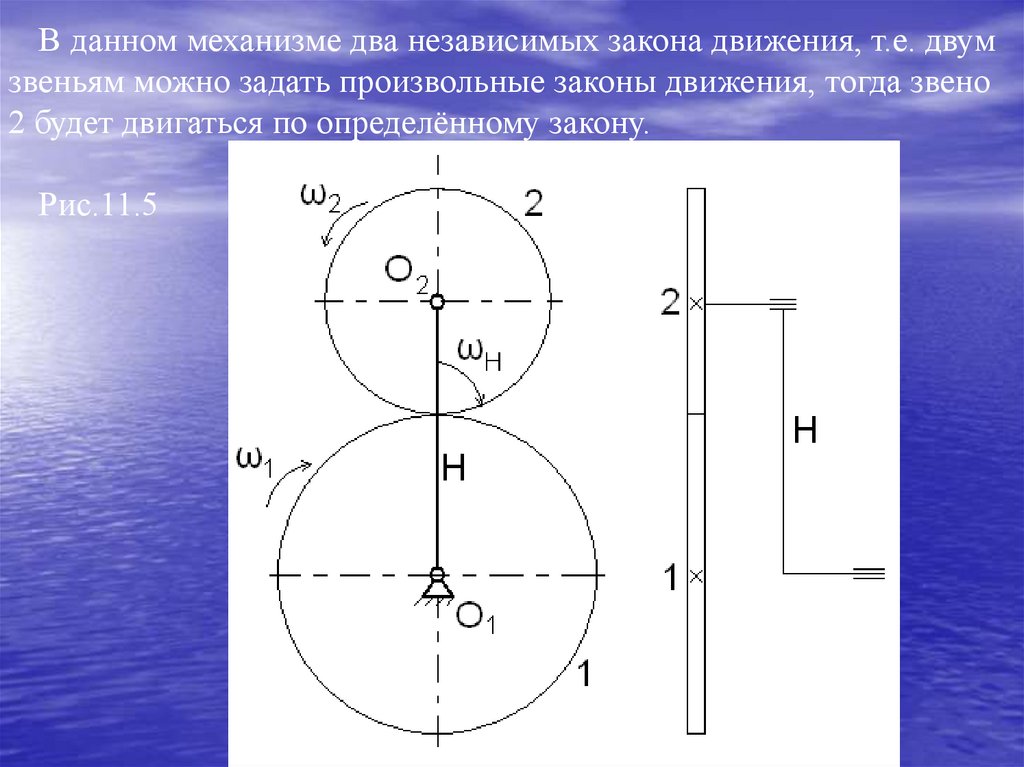
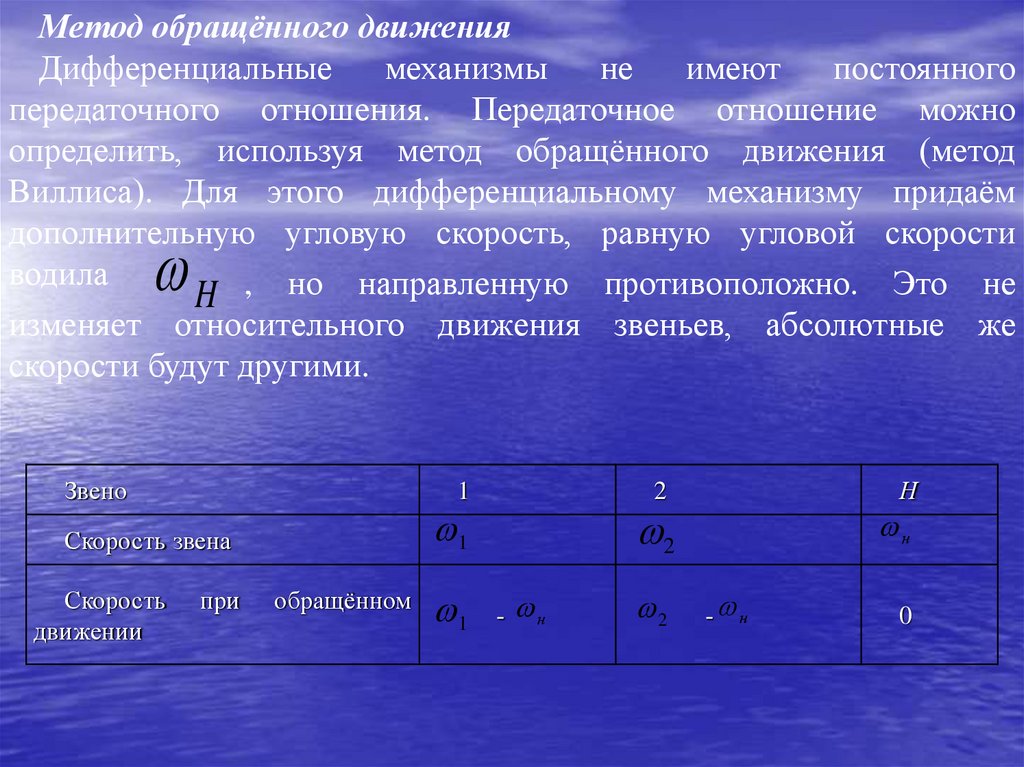



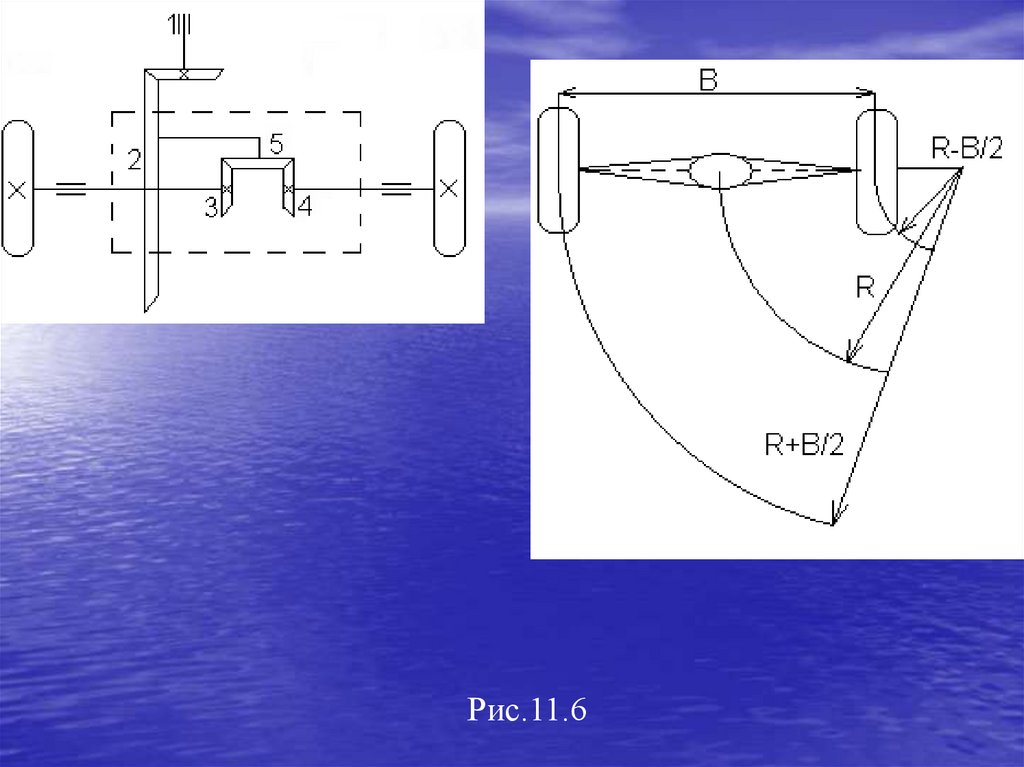


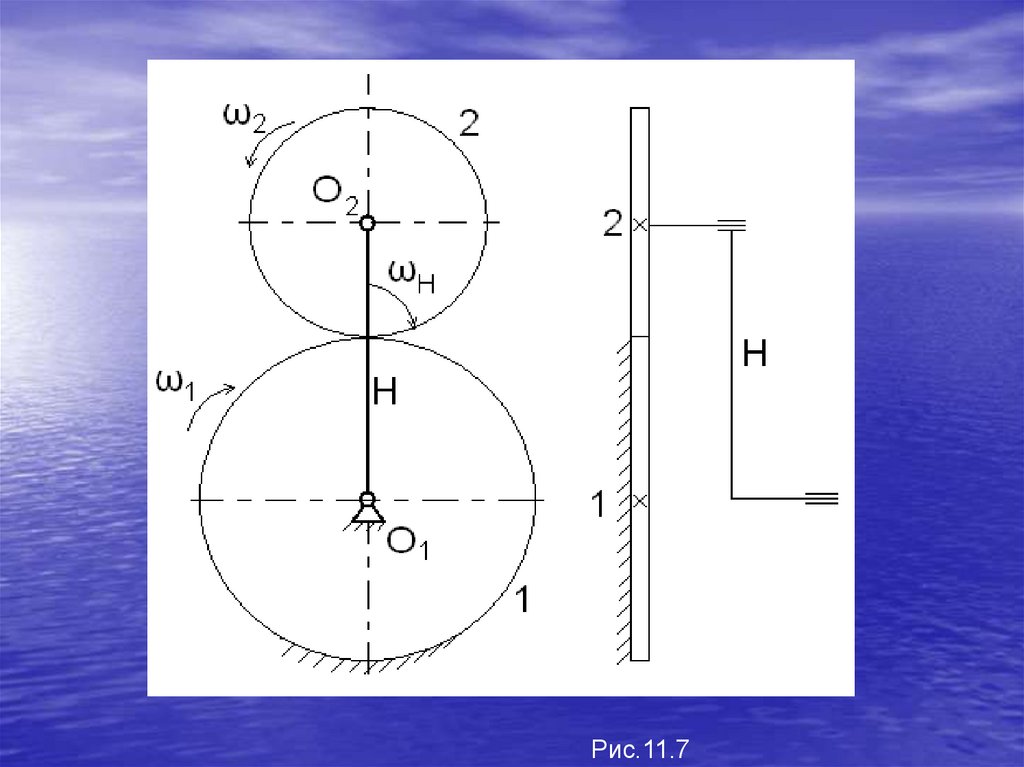
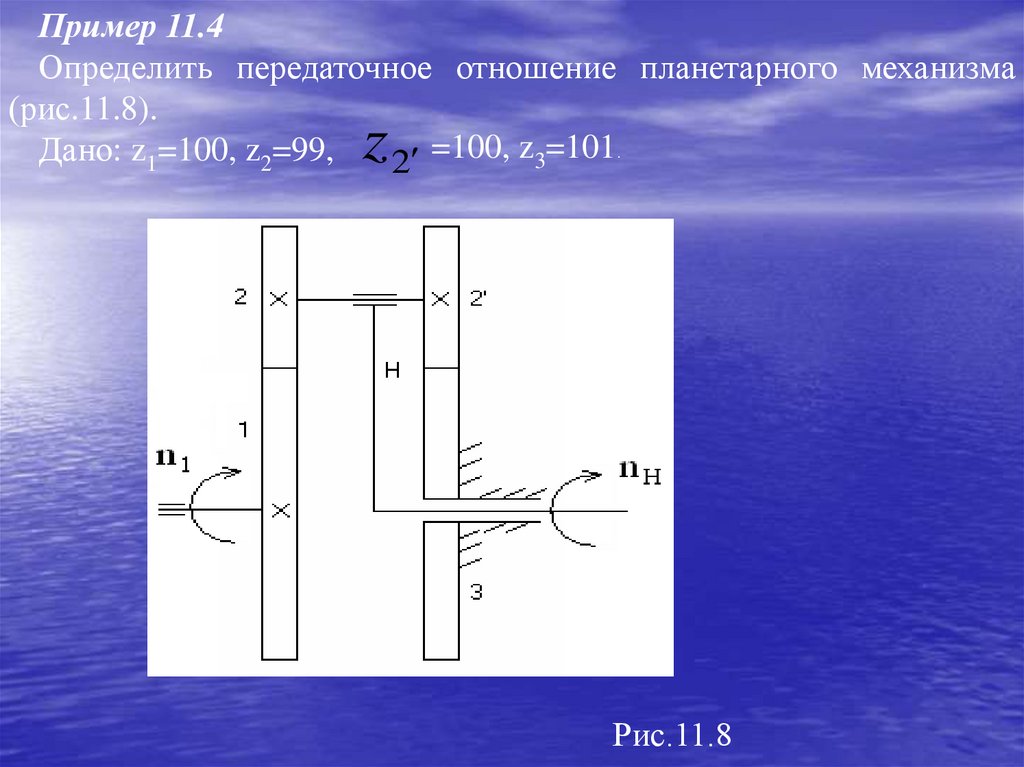





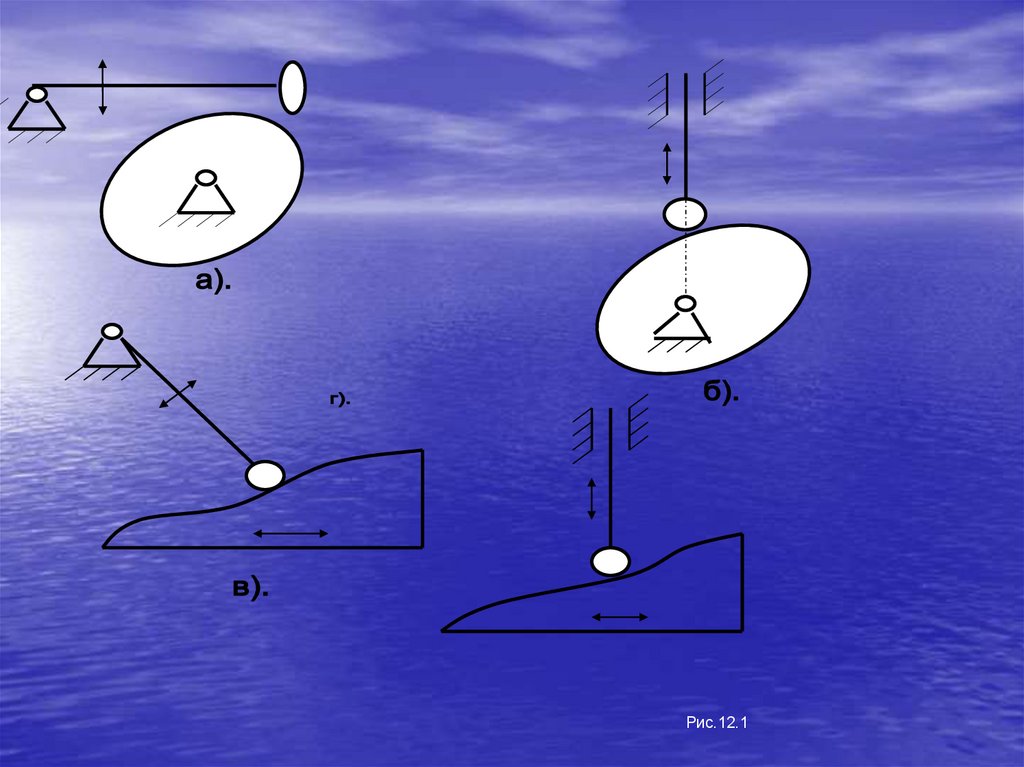


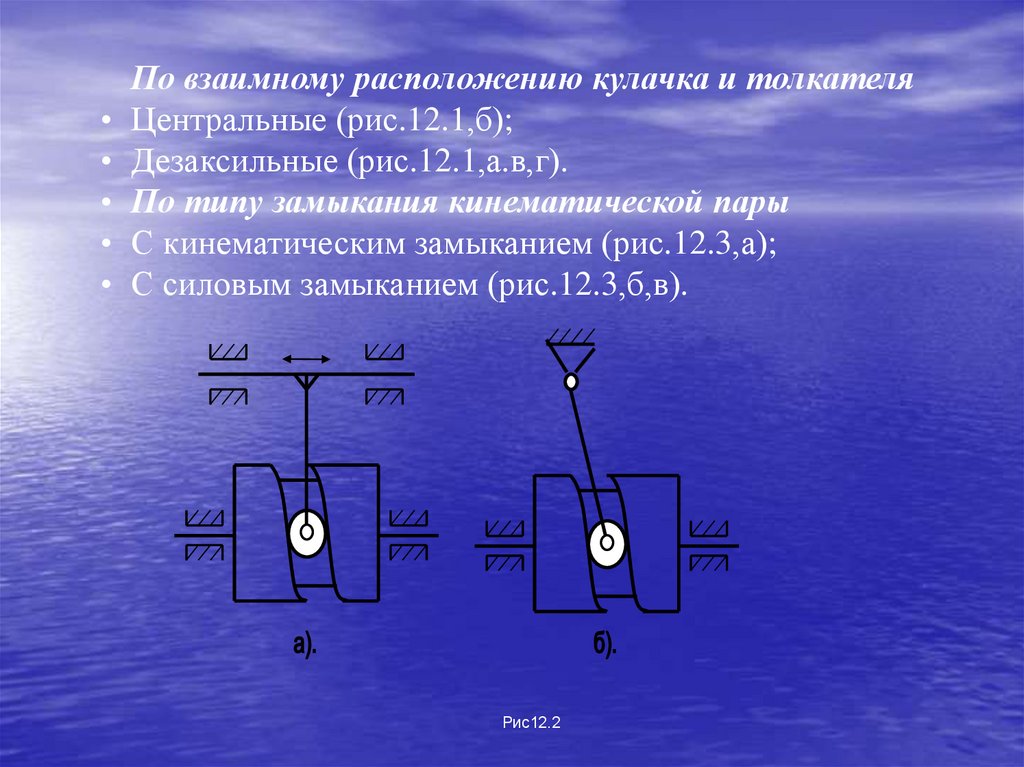
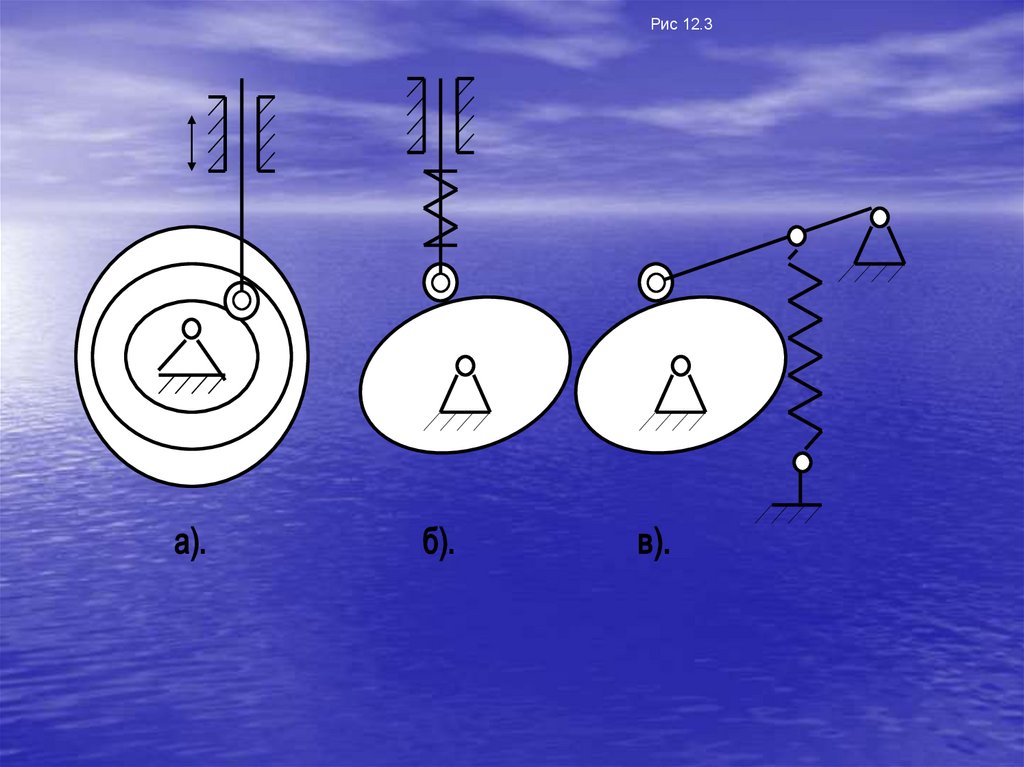
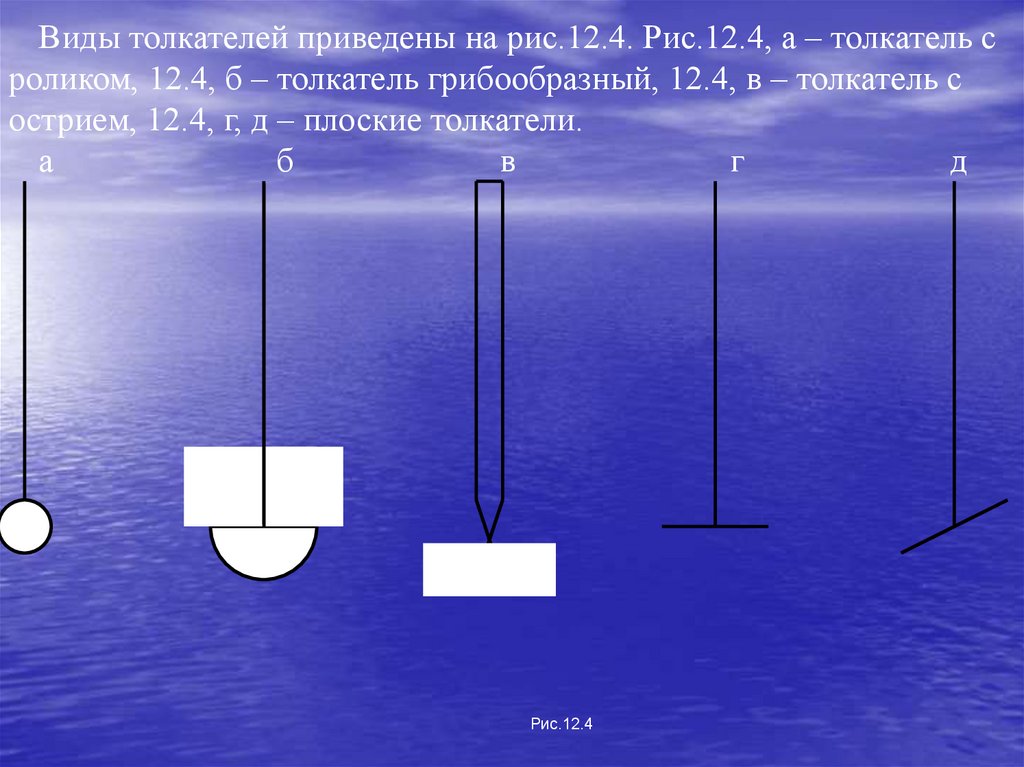





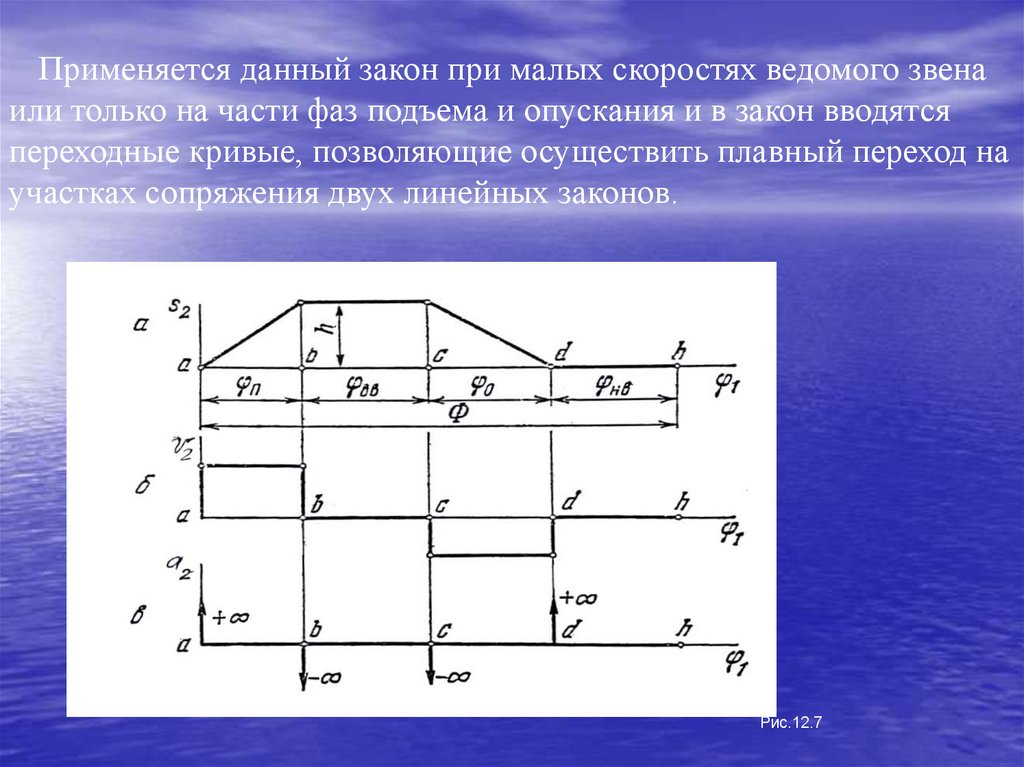
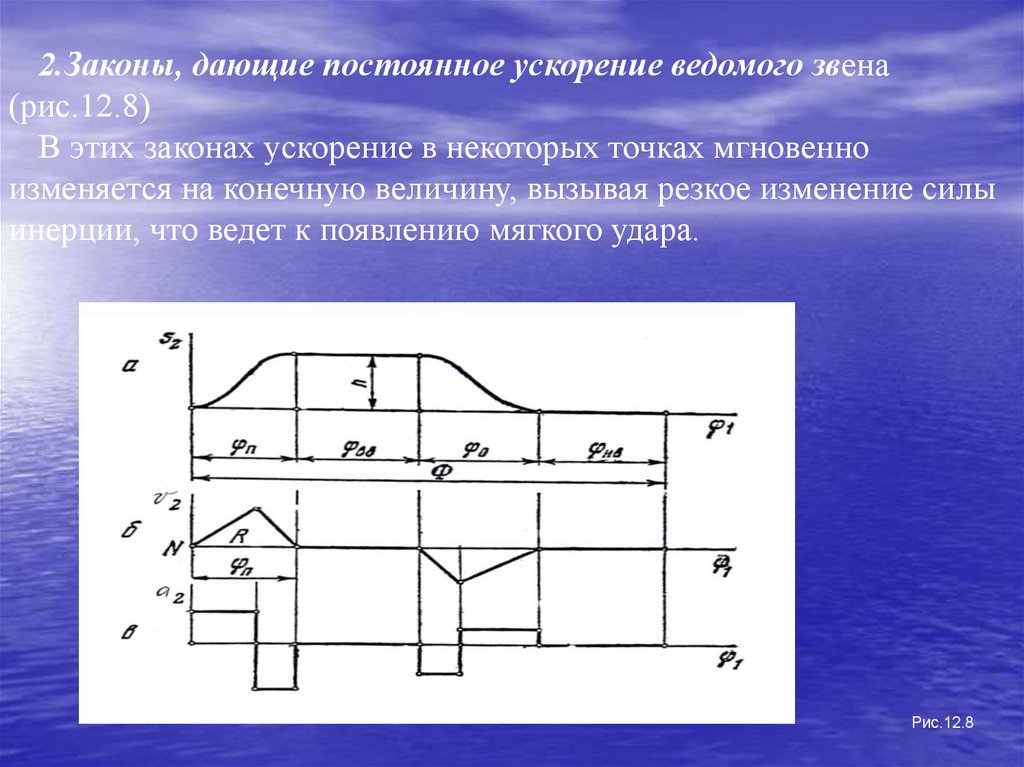
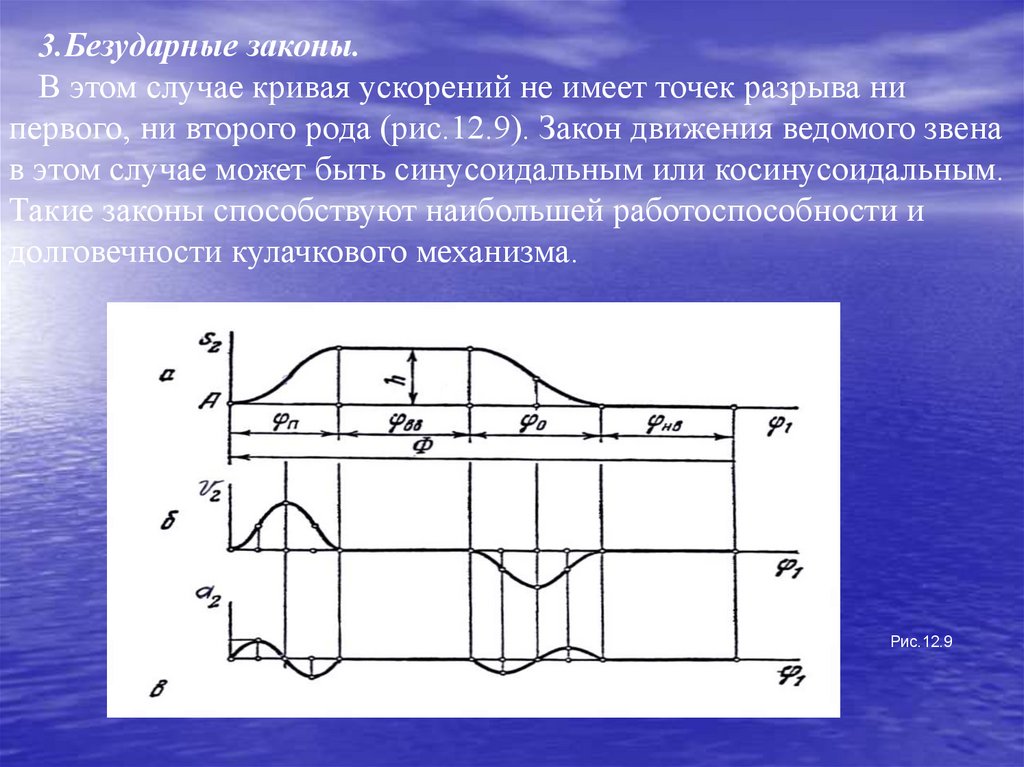


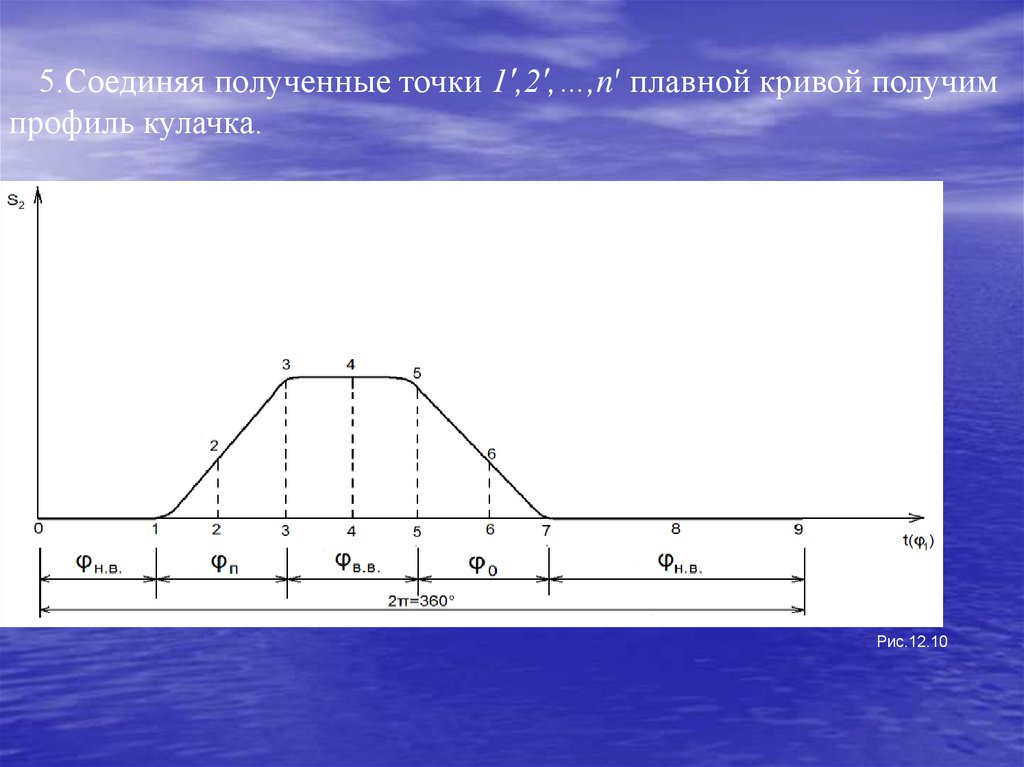




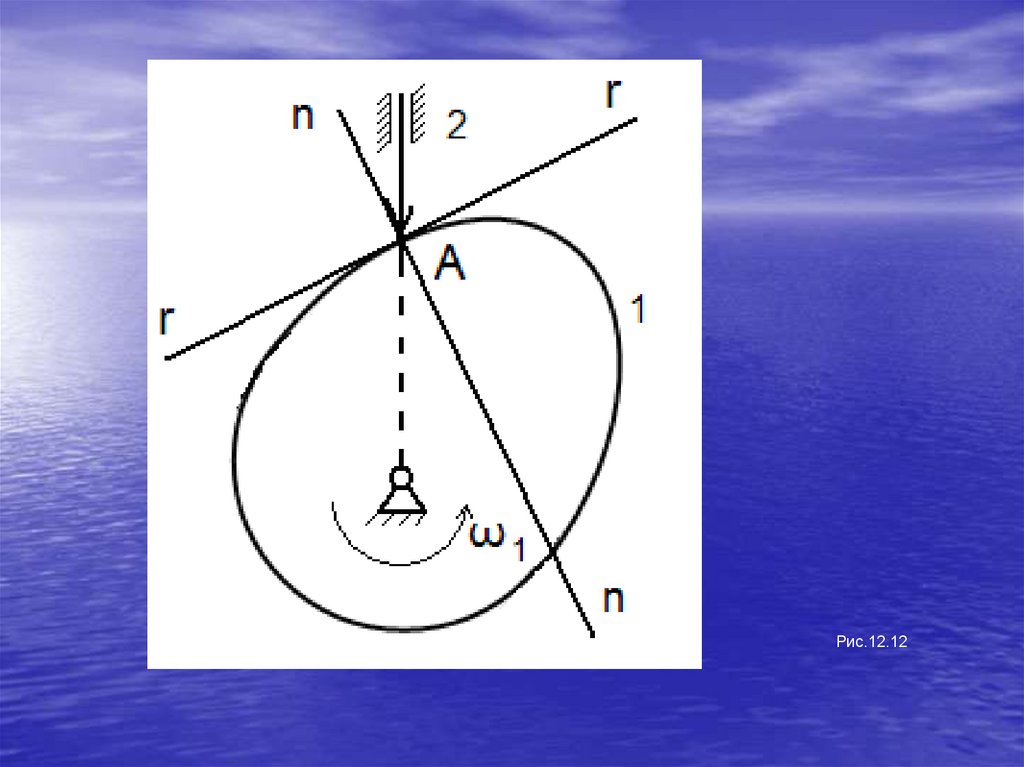







 Физика
Физика Механика
Механика








