Похожие презентации:
Элементы теории механизмов и машин
1.
1 Элементы теории механизмови машин
В учебной дисциплине теория механизмов
и машин изучаются свойства, анализ и
синтез типовых механизмов, независимо от
их назначения.
2.
1.1 Стадии проектирования иконструирования машин и
механизмов
3.
Процесс проектирования включает:• техническое задание – документ,
содержащий наименование,
назначение, технические требования
заказчика к изделию и другие
показатели;
4.
• техническое предложение –совокупность конструкторских
документов, обосновывающих
техническую и технико-экономическую
целесообразность разработки
различных вариантов изделия на основе
технического задания;
5.
• эскизный проект – совокупностьконструкторских документов,
содержащих принципиальные
конструкторские решения и чертежи
общих видов, в том числе и
пояснительную записку с
необходимыми расчетами;
6.
• технический проект – совокупностьконструкторских документов,
содержащих окончательное решение и
дающих полное представление об
устройстве изделия. Графическая часть
проекта состоит из чертежей общих
видов и сборочных чертежей узлов;
7.
• конструкторская документация –совокупность документов,
содержащих чертежи общих видов,
узлов и деталей, оформленных так,
чтобы по ним можно было изготовить
изделие и контролировать его в
процессе эксплуатации.
8.
Документация, разработанная врезультате процессов проектирования и
конструирования, называется проектом.
При разработке машин встречаются
расчёты двух видов:
• проектный (проектировочный);
• проверочный.
9.
Проектный расчёт выполняется подопускаемым напряжениям. При
проектном расчёте разрабатывают
конструкцию и определяют только
основные размеры деталей. Проектный
расчёт является упрощённым.
10.
Проверочный расчёт производят, когдаформа и размеры изделия известны из
проектного расчёта или были приняты
(заданы) конструктивно по таким
критериям работоспособности, как
прочность, жесткость, выносливость и т. д.
Проверочный расчёт является
уточненным.
11.
1.2 Классификация машин имеханизмов
Машина - это устройство для
преобразования энергии, материалов
или информации в механическое
движение с целью замены или
облегчения труда человека.
12.
По функциональному назначению всемашины условно подразделяются на:
• энергетические машины,
преобразующие любой вид энергии в
энергию механическую и наоборот
(двигатели, электрогенераторы и др.);
13.
• технологические машиныпреобразующие материалы,
изменяющие свойства, форму,
состояние и положение объектов
труда.
14.
• информационные машиныпредназначенные для получения и
преобразования информации,
выполнения контрольноизмерительных операции, а также для
регулирования и управления
технологическими процессами.
15.
Механизмы – системы твердых тел,подвижно соединенных друг с другом и
движущихся определенным, требуемым
образом относительно одного из них,
принятого за неподвижное тело.
16.
Механизмы в составе которыхприсутствуют жидкие или
газообразные тела соответственно
называются гидравлическими или
пневматическими.
17.
Качество машин (механизмов)характеризуют следующие показатели:
• работоспособность – состояние
изделия, при котором оно способно
нормально выполнять заданные
функции в соответствии с
параметрами, установленными
нормативной документацией;
18.
• надежность – свойство изделиявыполнять заданные функции,
сохраняя во времени значения
установленных эксплуатационных
показателей в пределах,
соответствующих заданным режимам
работы;
19.
• безотказность – состояние изделиясохранять работоспособность в
течение некоторого времени или при
выполнении определенного объема
работы без вынужденных перерывов
в заданных условиях эксплуатации;
20.
• долговечность – способностьизделия сохранять
работоспособность до определенного
состояния с необходимыми
перерывами для технического
обслуживания и ремонта;
21.
• технологичность – совокупностьряда признаков, обеспечивающих
экономичное и производительное
изготовление машины
прогрессивными методами при
одновременном повышении качества,
точности и взаимозаменяемости
составных частей;
22.
• ремонтопригодность –приспособленность машины к
предупреждению отказов и
неисправностей путем проведения
технического обслуживания, а также
возможность проведения ремонтов;
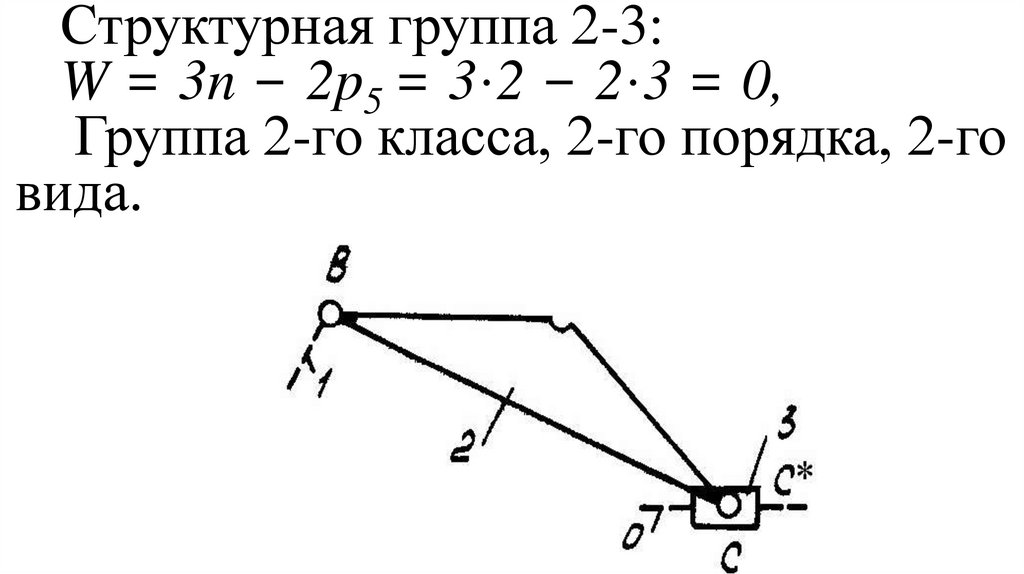
23.
• сохраняемость – свойство машинысохранять требуемые
эксплуатационные показатели после
установленного срока хранения и
транспортирования;
24.
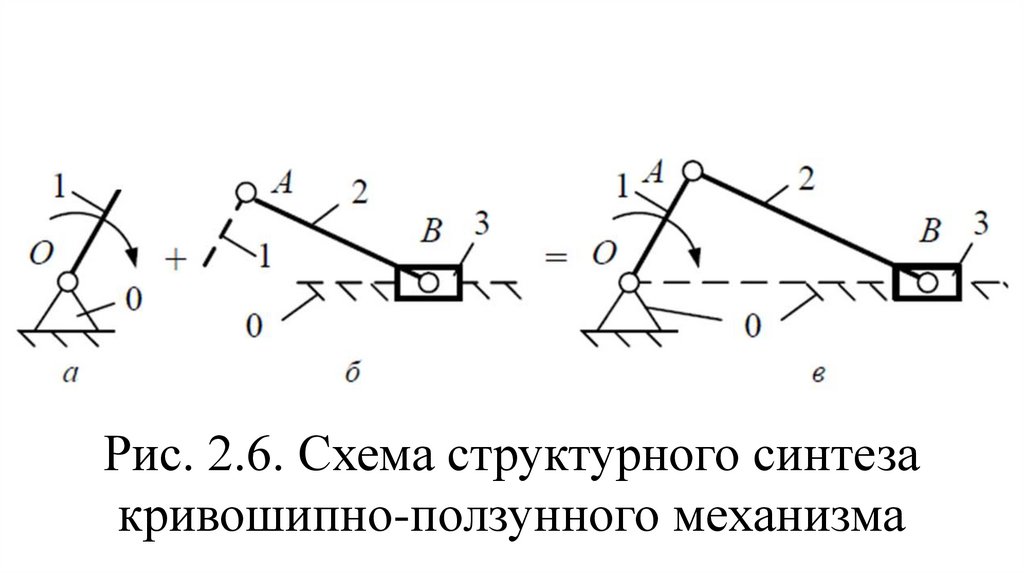
• эргономичность – совокупностьсвойств машины, обеспечивающих
красоту ее внешних форм, удобство
обслуживания и эксплуатации.
25.
1.3 Основные характеристикимашин и механизмов
К характеристикам относятся:
назначение, область применения, способ
управления, мощность,
производительность, коэффициент
полезного действия, масса, габаритные
размеры, стоимость и др.
26.
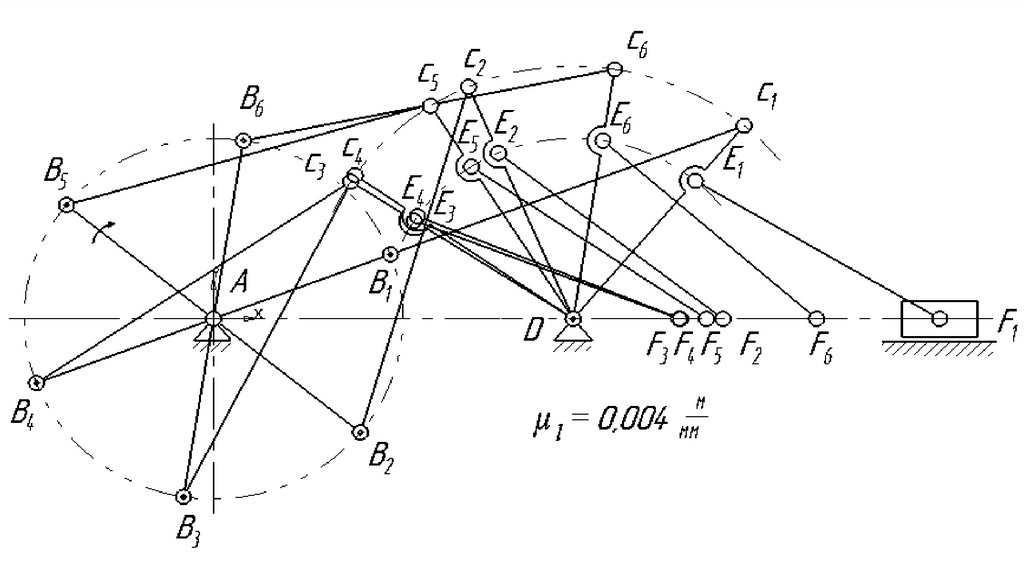
Механизмы предназначенные для изменения скорости движения деталеймашин при сохранении вида движения
(передачи) характеризуются
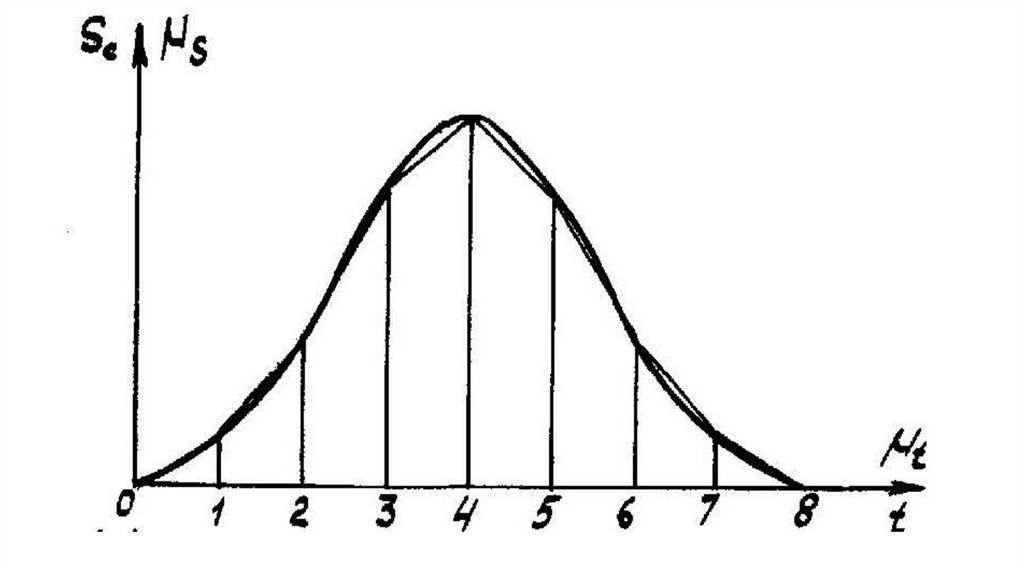
передаточным отношением u.
27.
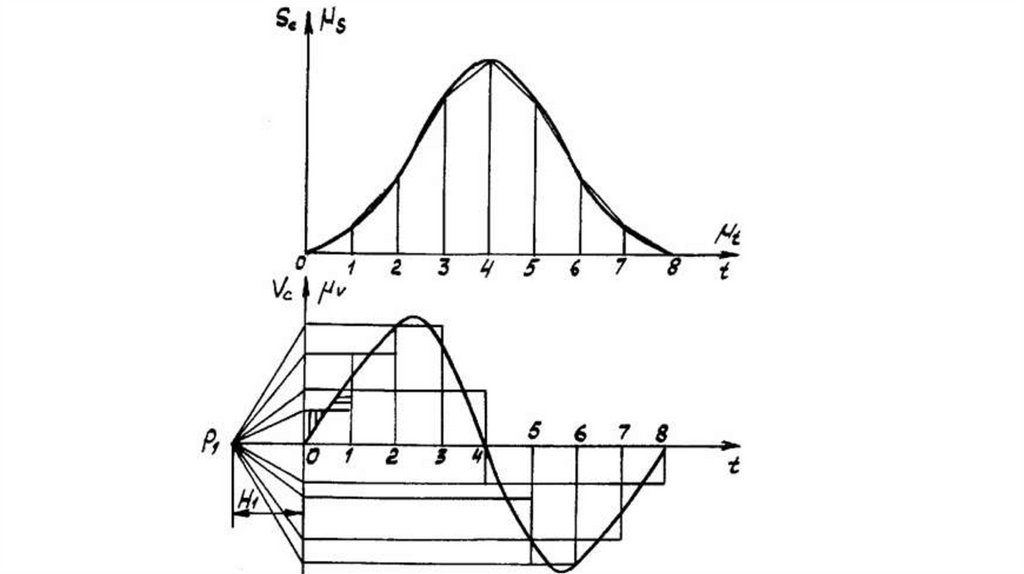
Передаточное отношение uопределяется как отношение угловых
скоростей входного и выходного
звеньев механизма, т.е. u = пв / пвых, или
u = ωвх/ ωвых. Угловая скорость звеньев
задается в оборотах в минуту (п) или
в радианах в секунду (ω=2πп/60).
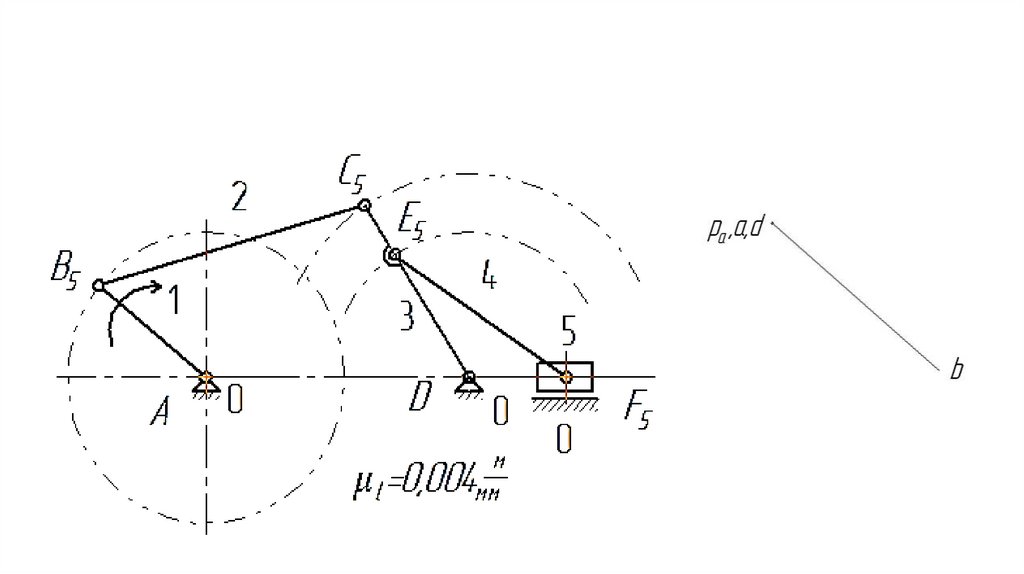
28.
Механизмы, предназначенные дляпонижения угловой скорости ведущих
звеньев называют редукторами.
Механизмы для повышения угловой
скорости ведущих звеньев называют
мультипликаторами.
29.
Механизмы для преобразования однихвидов движений в другие делят на
шарнирно-рычажные, фрикционные,
зубчатые, кулачковые, винтовые, с
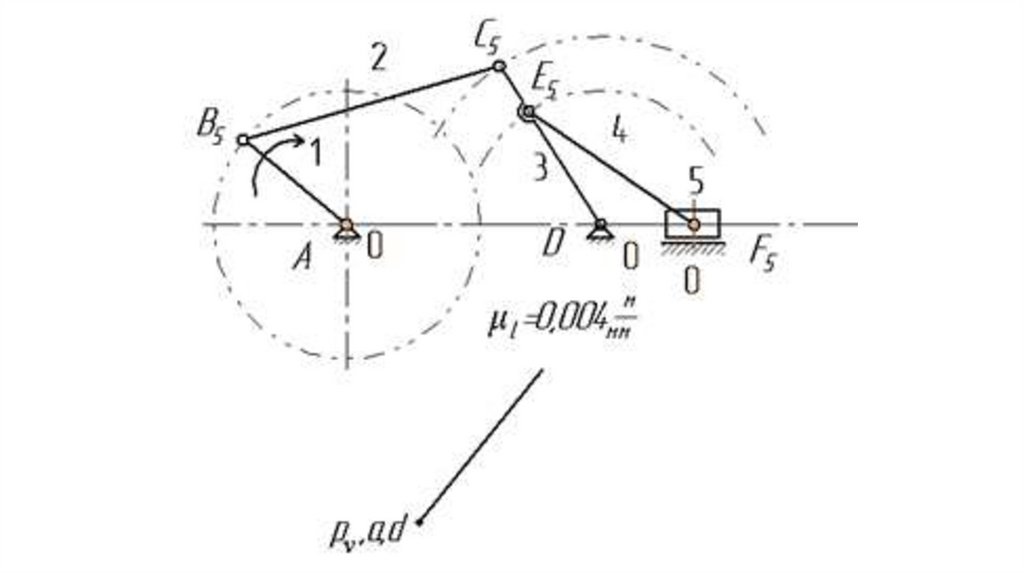
гибкими звеньями, а также механизмы
прерывистого движения.
30.
Механизмы могут быть предназначенытолько для преобразования параметров
движения (кинематические механизмы)
или только для преобразования сил
(силовые механизмы), или для того и
другого одновременно.
31.
Эффективость работы механизмовхарактеризуется коэффициентом
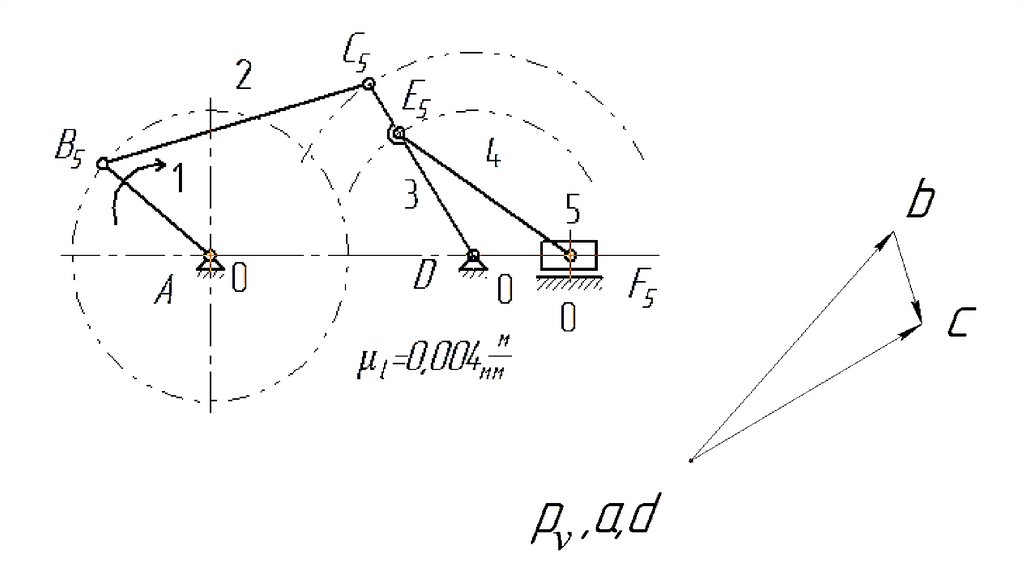
полезного действия равным
отношению мощностей на выходном и
входном звеньях механизма.
32.
1.4 Составные части механизмаМеханизмы состоят из звеньев
подвижно соединенных друг с другом с
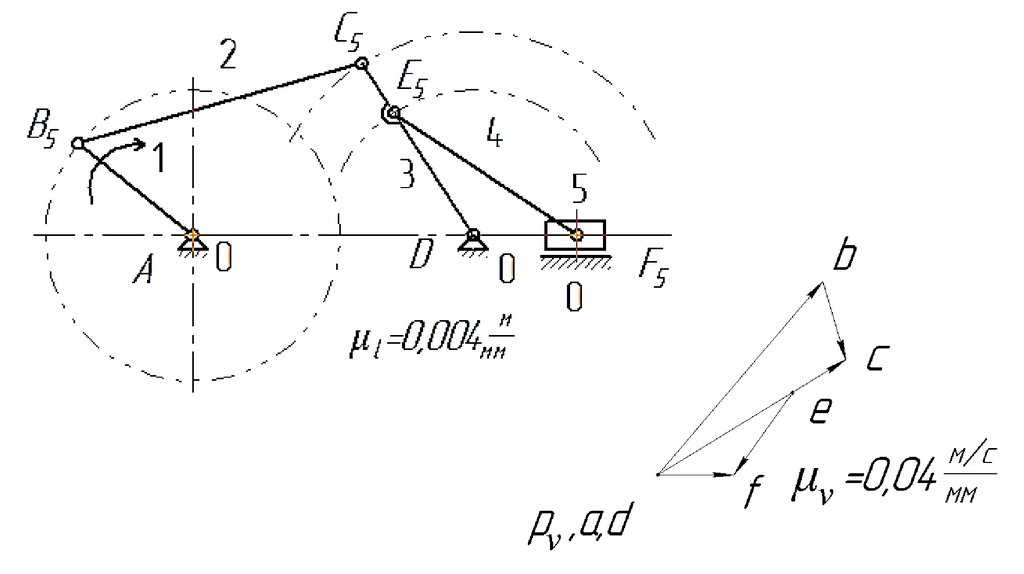
помощью кинематических пар.
Звено – это деталь или группа деталей,
жестко соединенных между собой.
Звенья могут быть жесткими и гибкими
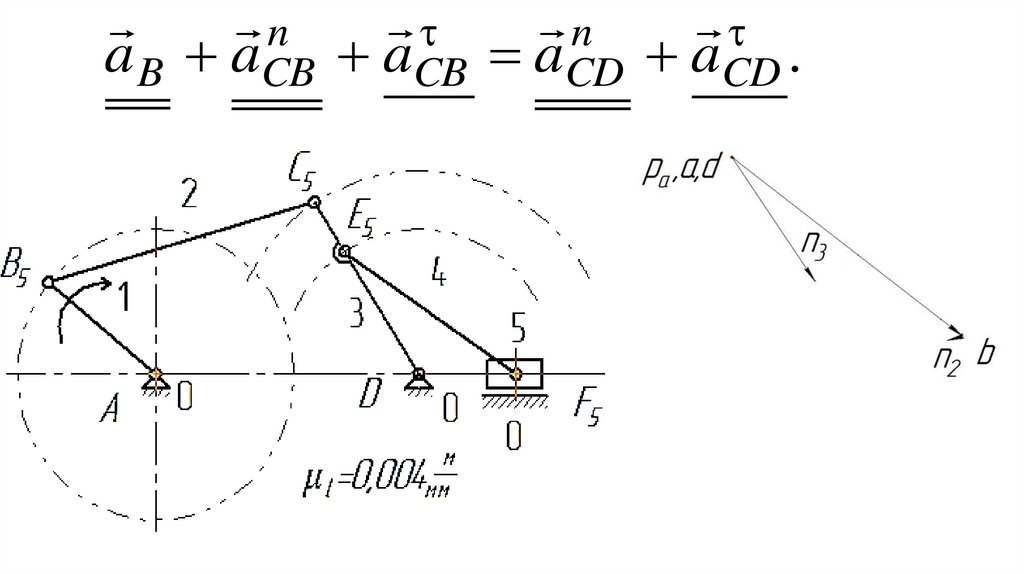
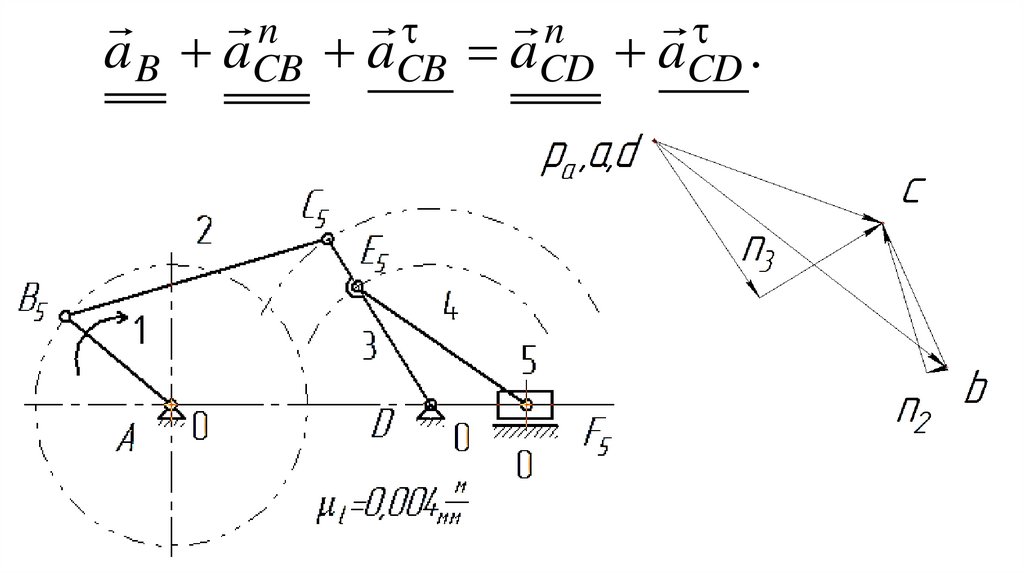
(тросы, ремни, цепи).
33.
Кинематическая пара – этоподвижное соединение двух
соприкасающихся звеньев,
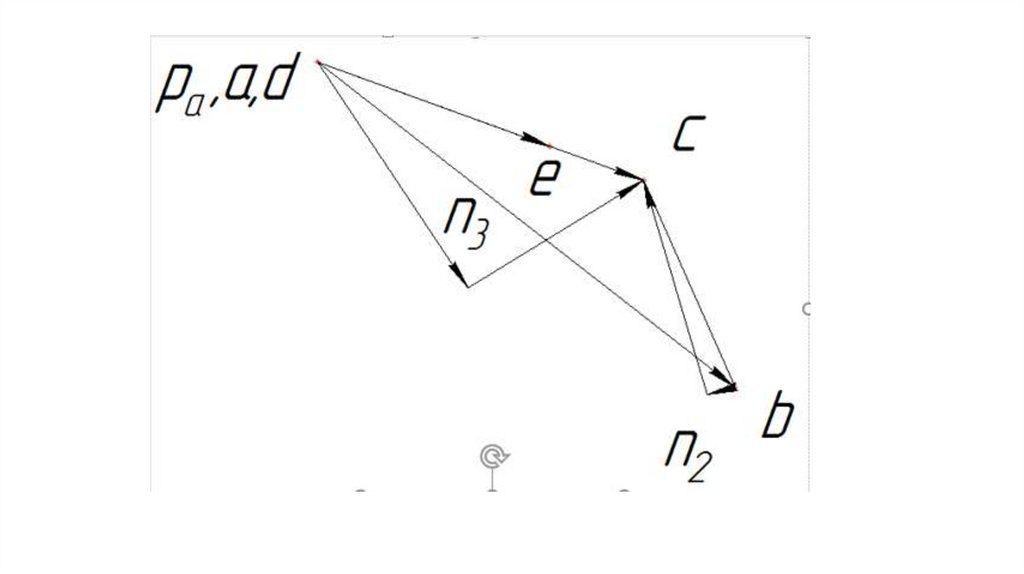
допускающее движение их
относительно друг друга.
34.
Неподвижное звено механизма (илизвено, условно принимаемое за
неподвижное), называют стойкой.
Стойкой может быть станина, корпус,
рама или другое изделие. Относительно
стойки оценивают параметры движения
подвижных звеньев механизма.
35.
Механизмы могут иметь нескольковходных и выходных звеньев.
Звено, движение которому
сообщается извне, называют ведущим
(входным). Звено, движение которому
передается от входного звена
посредством других промежуточных
звеньев - ведомое (выходное).
36.
Положения всех звеньев механизмаотносительно неподвижного звена
задаются обобщенными координатами,
полностью и однозначно
определяющими положение механизма.
Количество обобщенных координат
соответствует количеству степеней
подвижности механизма.
37.
Звено, координаты котороговыбираются в качестве обобщенных
координат механизма, называется
начальным звеном. В большинстве
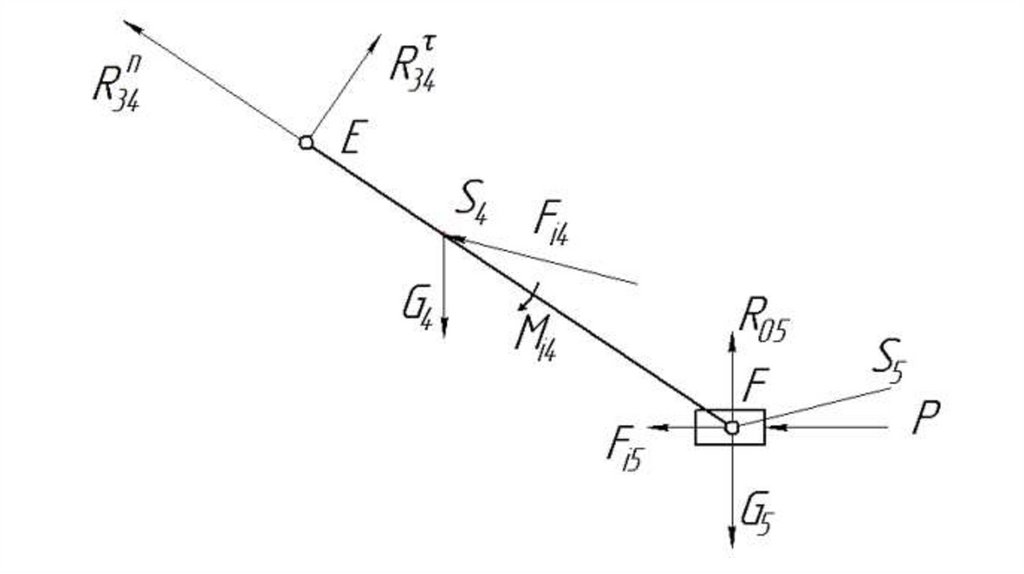
случаев начальное звено совпадает с
входным звеном.
38.
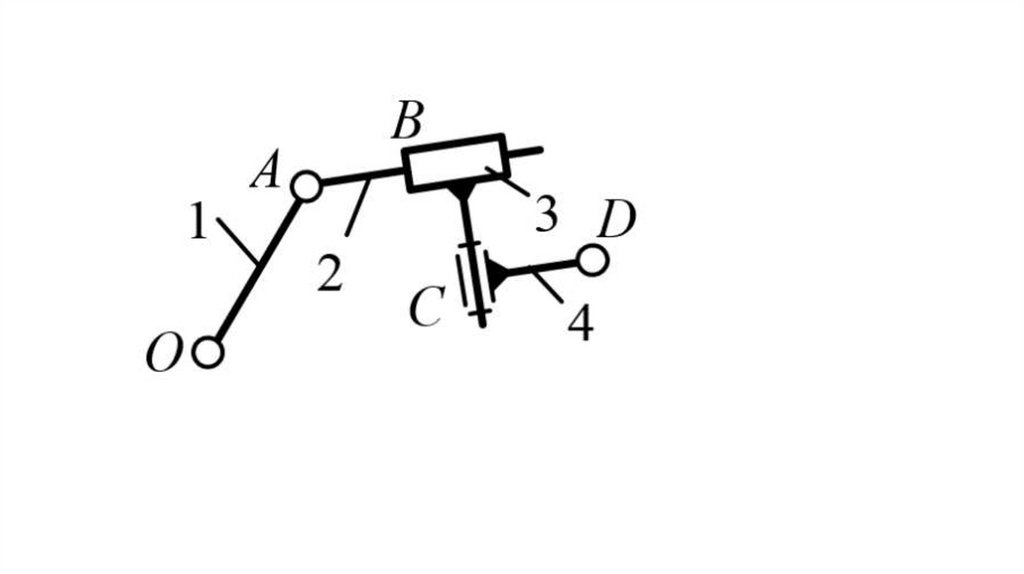
Примером плоскогорычажного механизма
является шарнирный
четырехзвенник, у
которого 1, 2, 3, 4 звенья; А, В, С, D кинематические пары.
39.
Положение подвижных звеньев 1, 2 и 3механизма, имеющего одну степень
свободы, полностью и однозначно
определяется одной координатой –
углом поворота φ1 входного звена 1
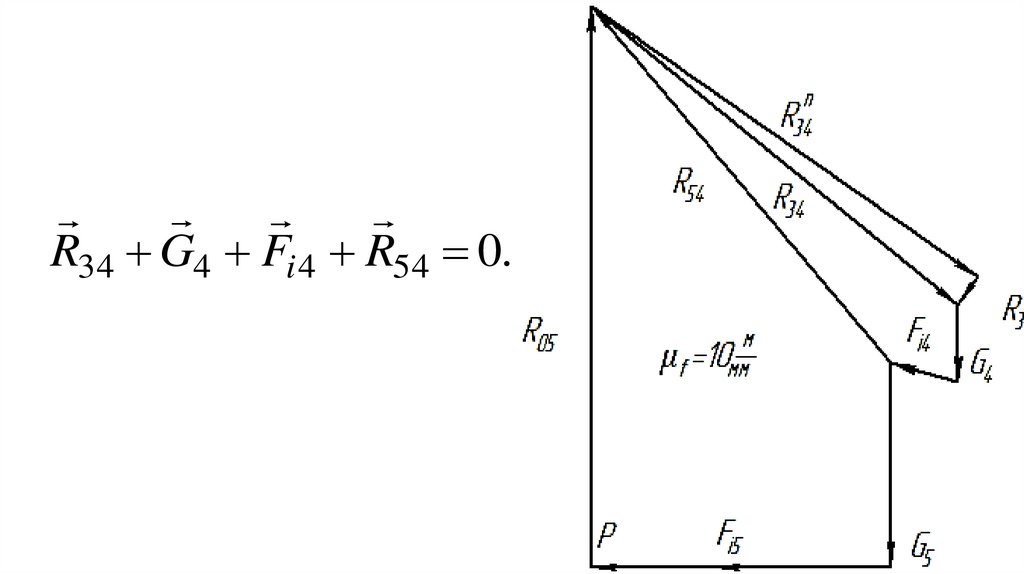
(φ1 можно принять за обобщенную
координату).
40.
В зависимости от характера движениязвенья рычажных механизмов именуют:
кривошип - звено, совершающее
полнооборотное вращательное
движение вокруг неподвижной оси;
коромысло - звено, совершающее
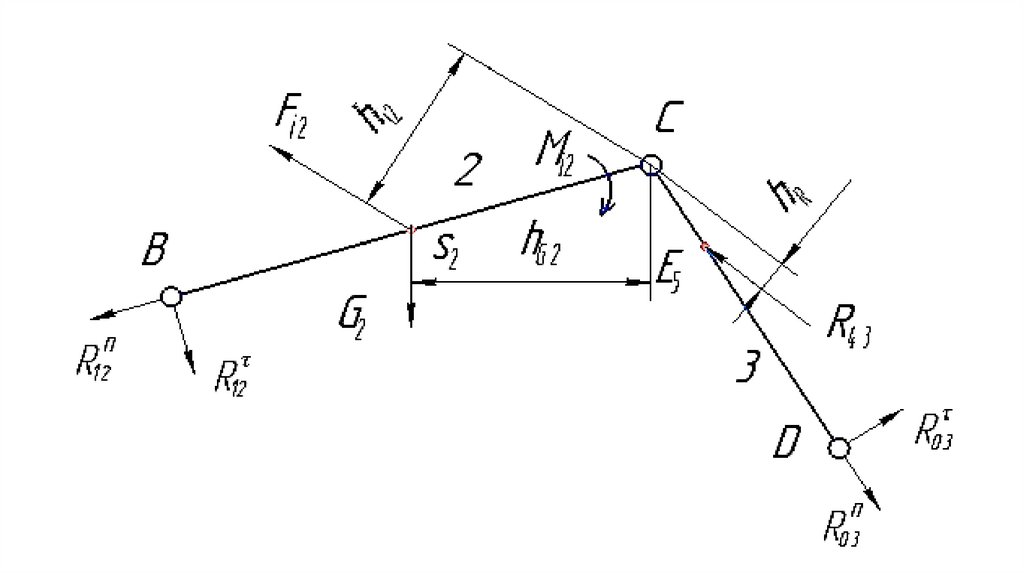
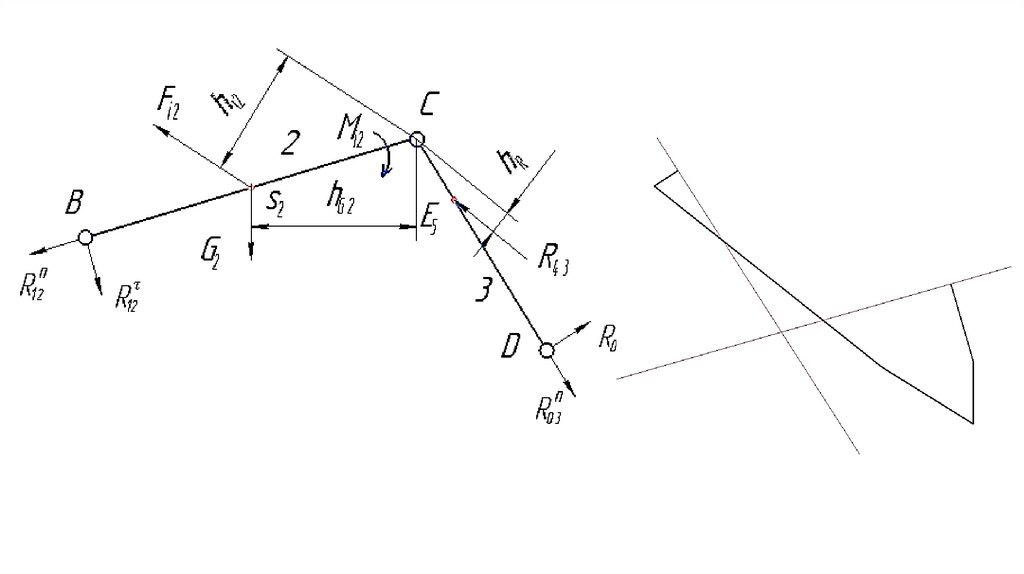
вращательное движение на неполный
оборот;
41.
кулиса - звено рычажного механизма,вращающееся (качающееся) вокруг
неподвижной оси, кулиса является
подвижной направляющей для камня;
камень - ползун, перемещающийся по
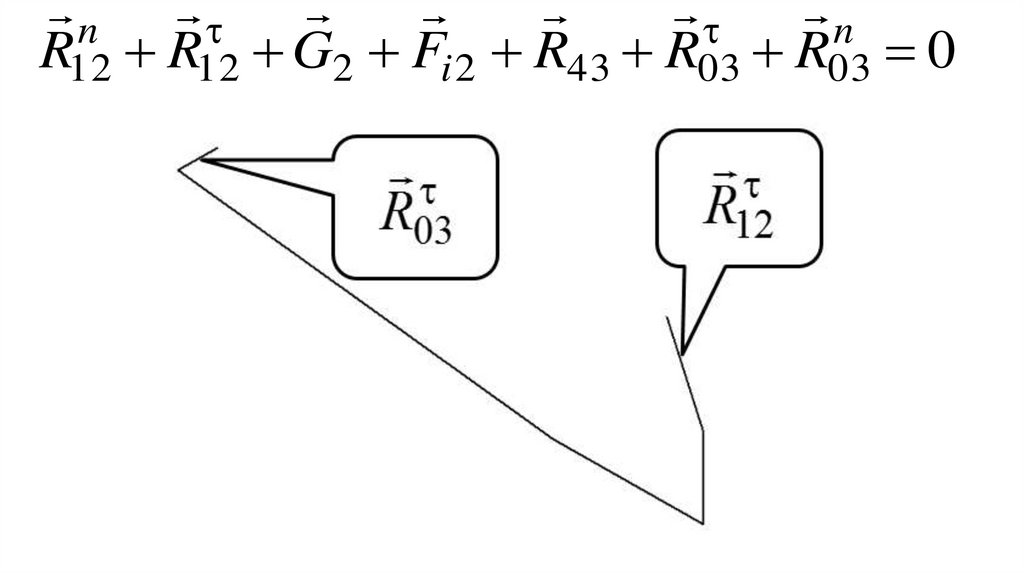
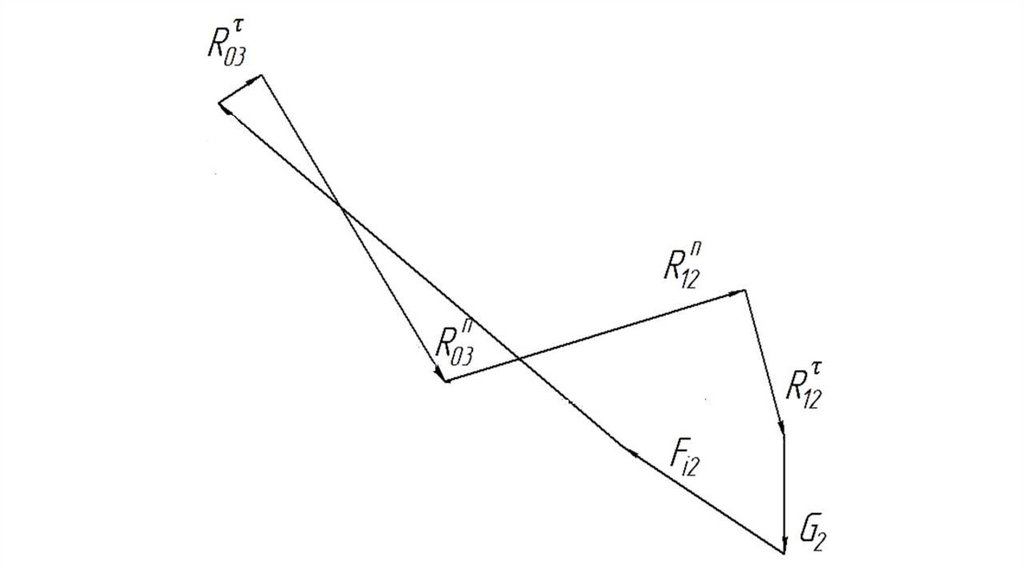
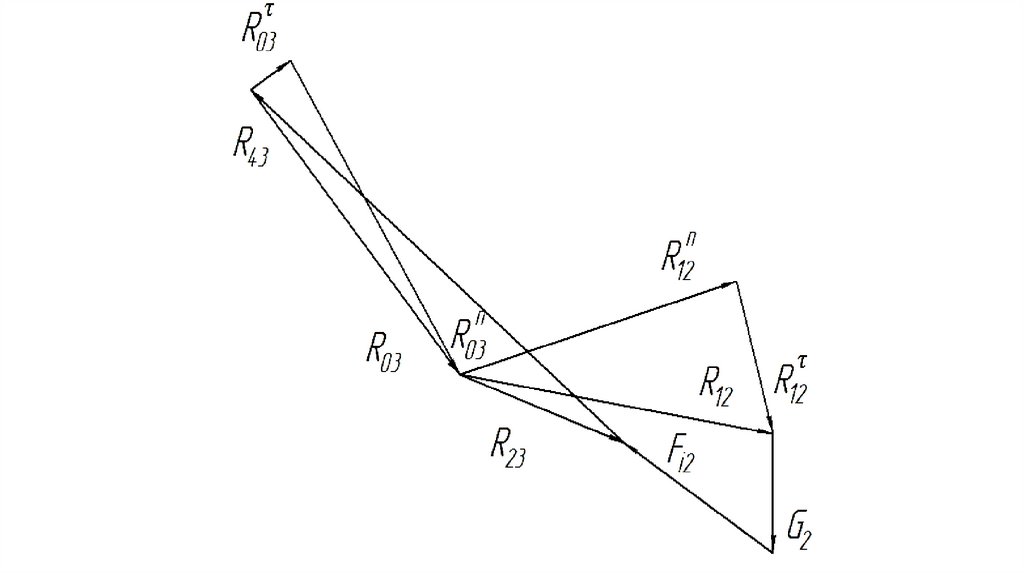
кулисе;
стойка - неподвижное звено
механизма.
42.
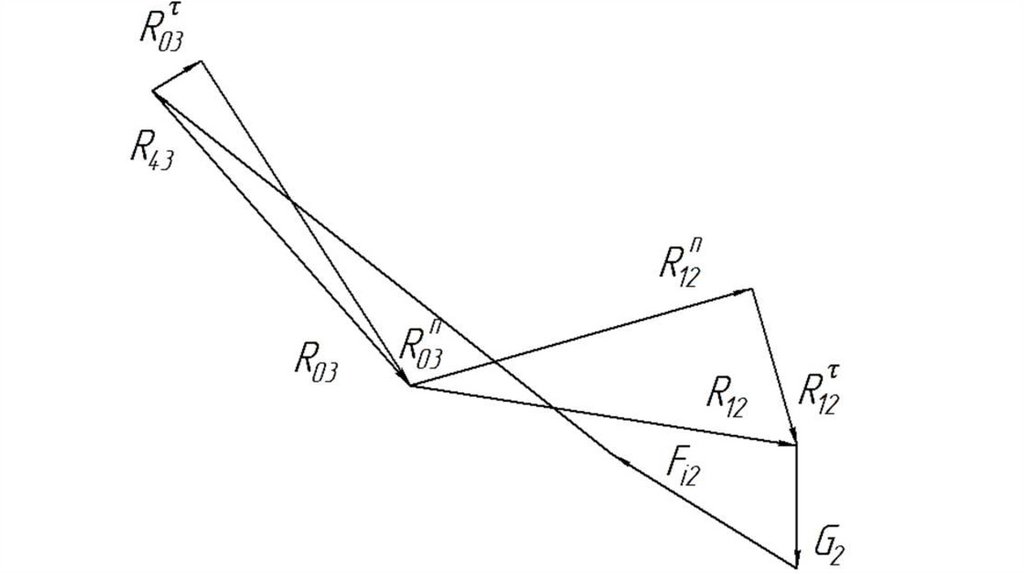
ползун - звено, совершающеевозвратно-поступательное движение по
неподвижной направляющей;
шатун - звено, совершающее
одновременно вращательное и
поступательное движение.
43.
1.5 Классификациякинематических пар
Кинематические пары подразделяются на
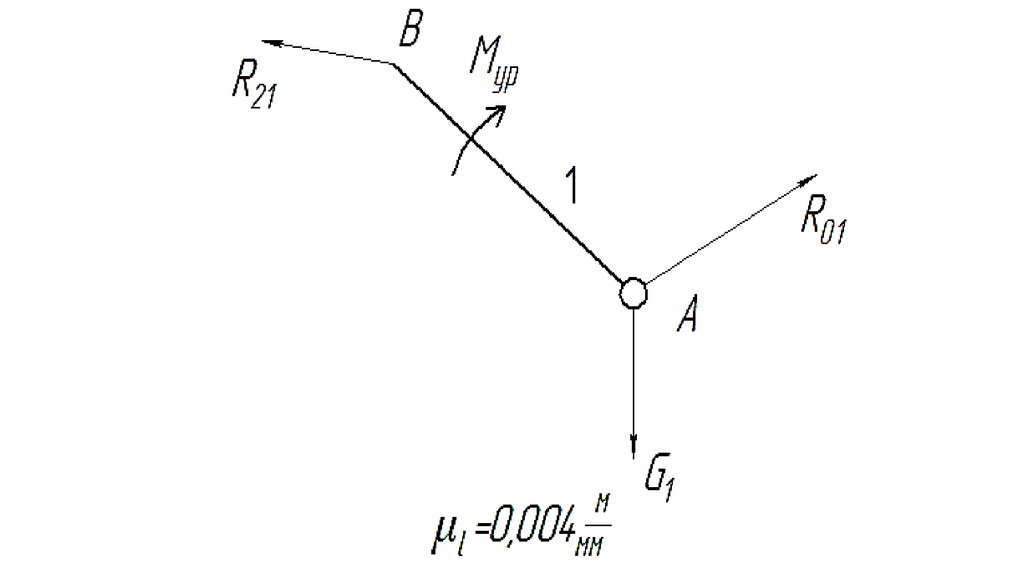
классы в соответствии с количеством связей,
накладываемых на относительное
движение соединенных в данную
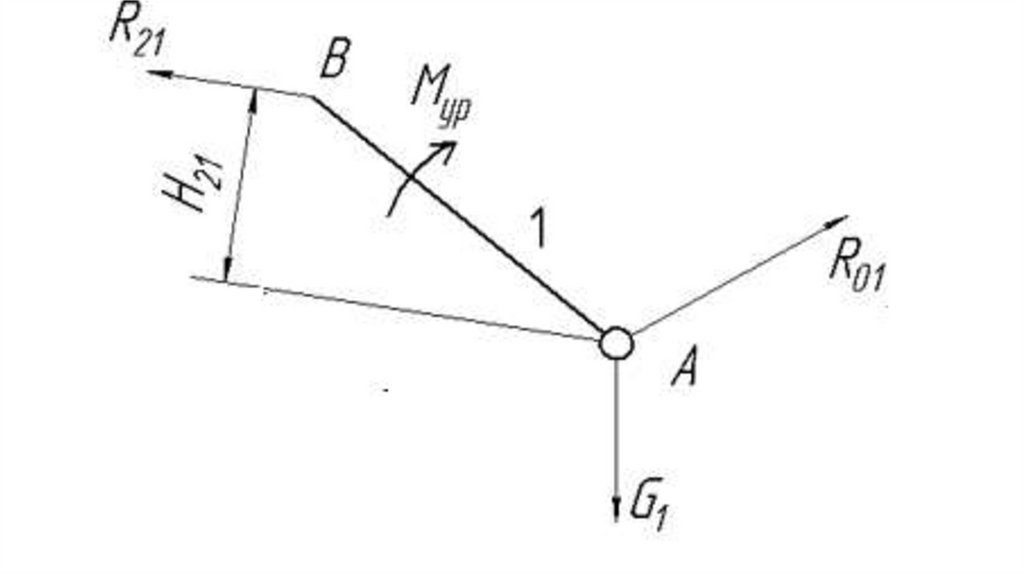
кинематическую пару звеньев.
44.
При этом приняты следующиеобозначения:
W – число степеней свободы;
S – количество связей, накладываемых
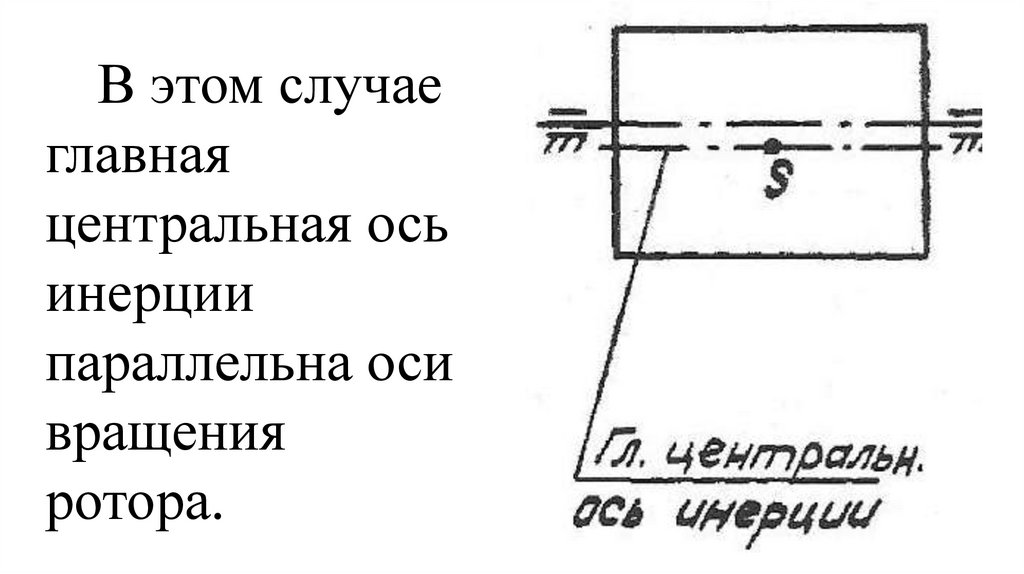
на относительное движение звеньев.
45.
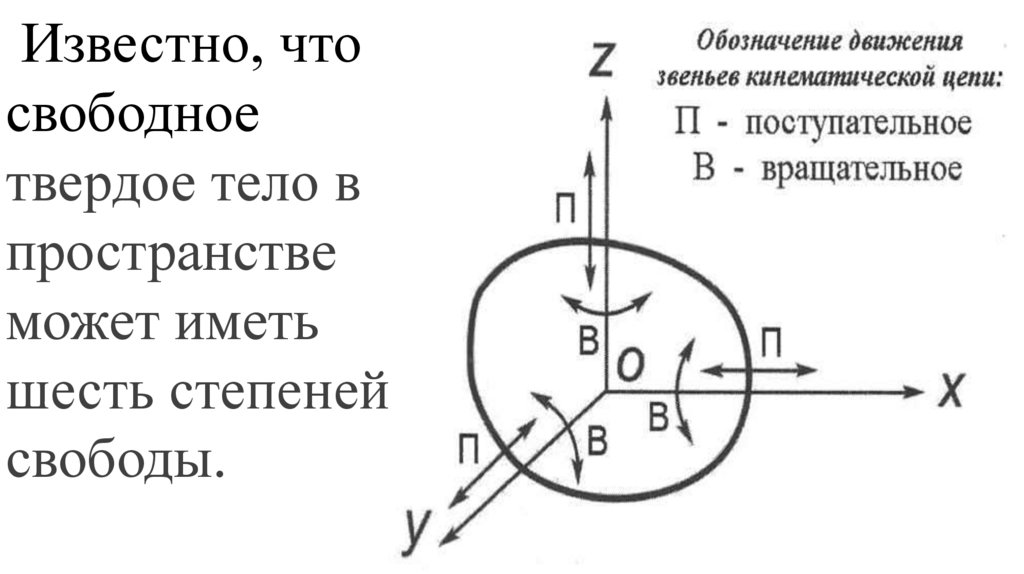
Известно, чтосвободное
твердое тело в
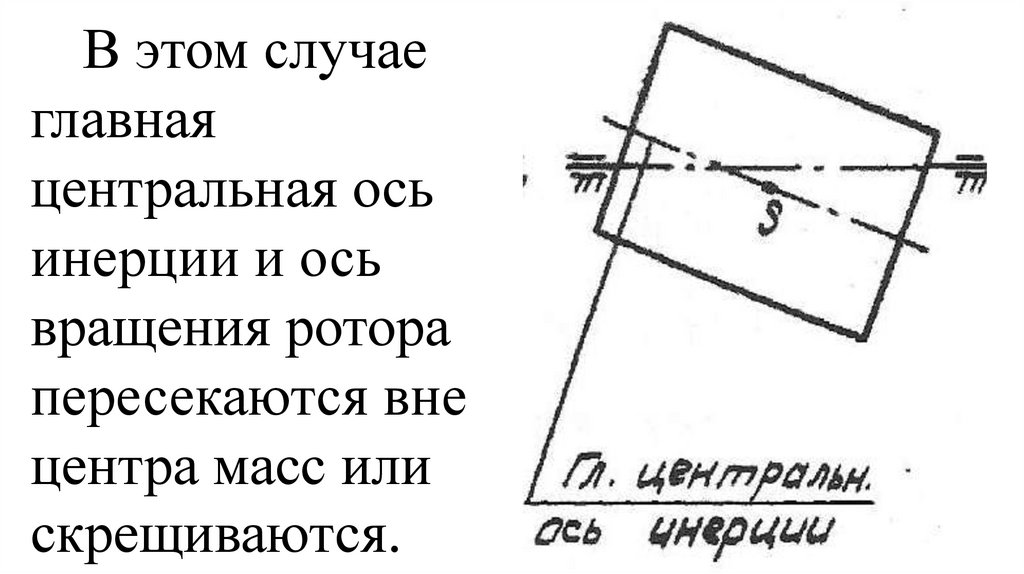
пространстве
может иметь
шесть степеней
свободы.
46.
Перемещение тела в пространствеможно представить как результат
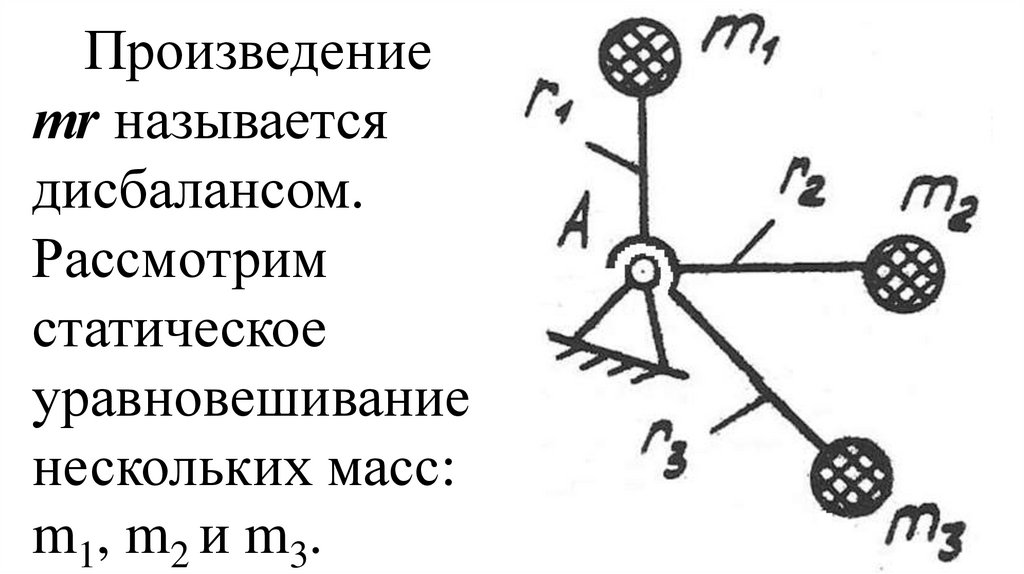
сложения шести независимых
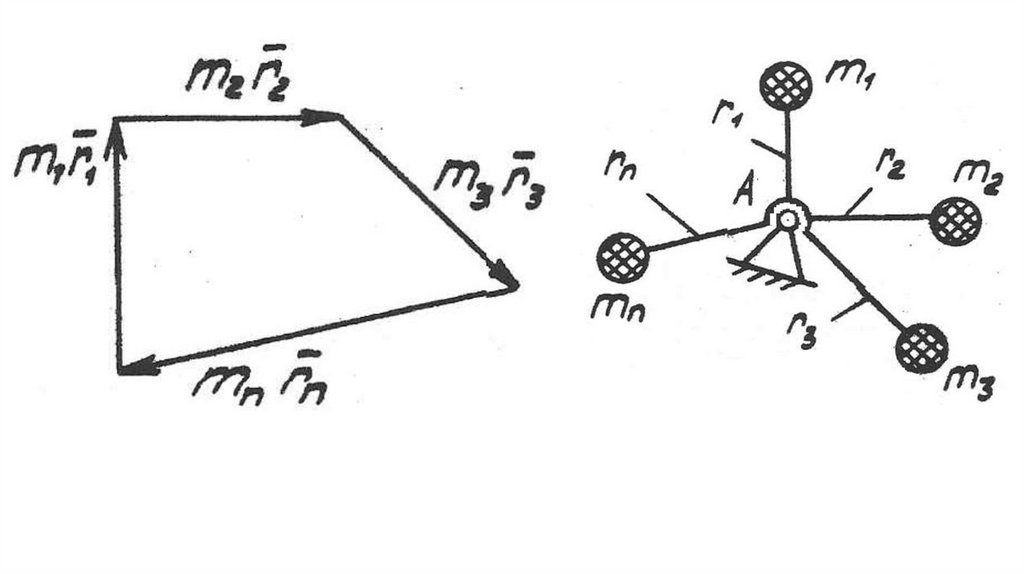
движений, а именно, трех
поступательных параллельно осям
координат OX, OY, OZ и трех
вращательных относительно этих осей.
47.
Всякая кинематическая параограничивает движение соединяемых
звеньев. Ограничение, накладываемое
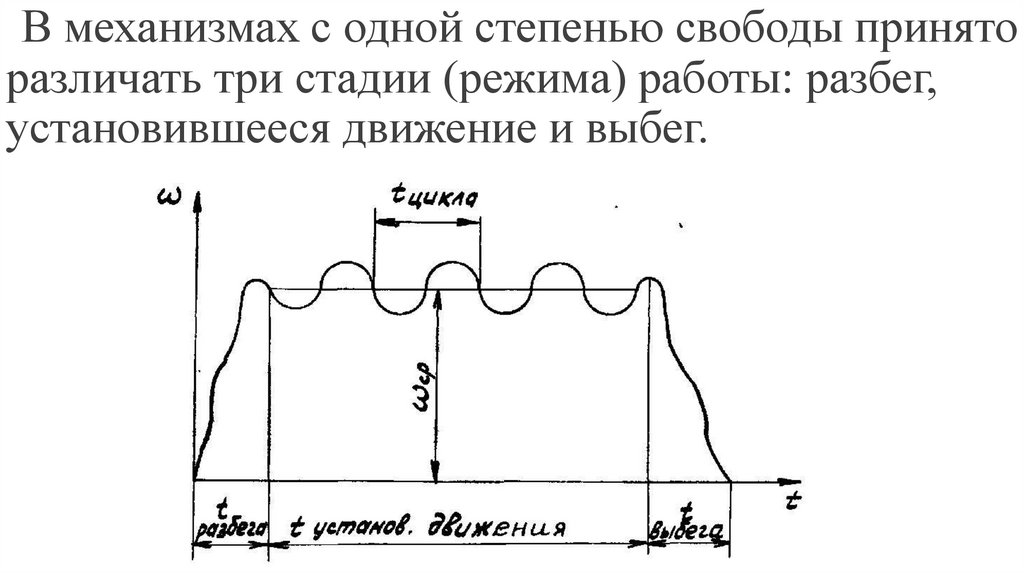
на движение твердого тела, называется
условием связи.
Каждое одно условие связи
устраняет одну степень свободы.
48.
Количество связей S,ограничивающих движения звеньев,
определяется равенством:
где Н - число степеней подвижности
кинематической пары (число
независимых движений одного звена
относительно другого).
49.
Кинематические пары делят на пятьклассов в зависимости от числа связей S
(изменяющихся от 1 до 5) или от
степени подвижности Н.
При S = 6 кинематическая пара
превращает подвижные звенья в одно
жесткое звено.
При S = 0 кинематической пары не
существует.
50.
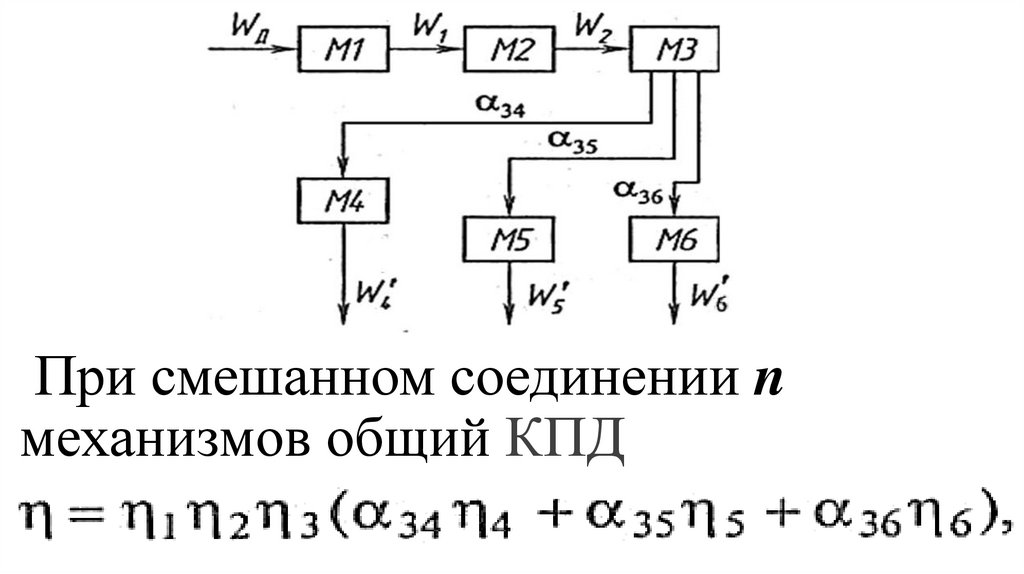
Пример кинематической пары 1-гокласса — шар на плоскости. Шар
можно вращать вокруг осей х, у, z и
перемещать его
вдоль осей х и у.
S = 6 - 5 =1.
51.
Пара "цилиндр наплоскости"
является парой 2го класса, где Н=4,
S=2 (невозможны
движения вдоль
оси Z и вокруг
оси Y).
52.
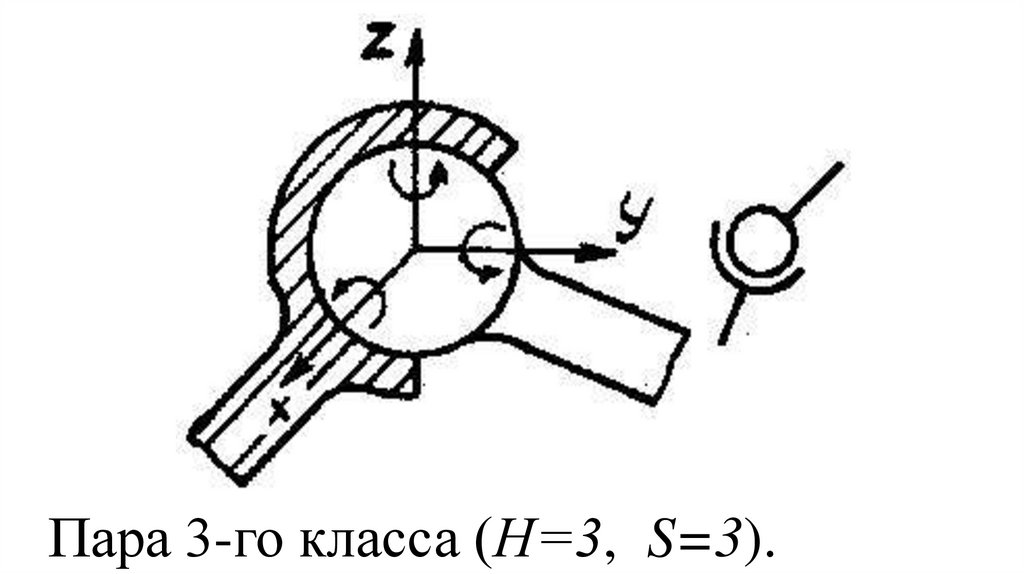
Пара 3-го класса (Н=3, S=3).53.
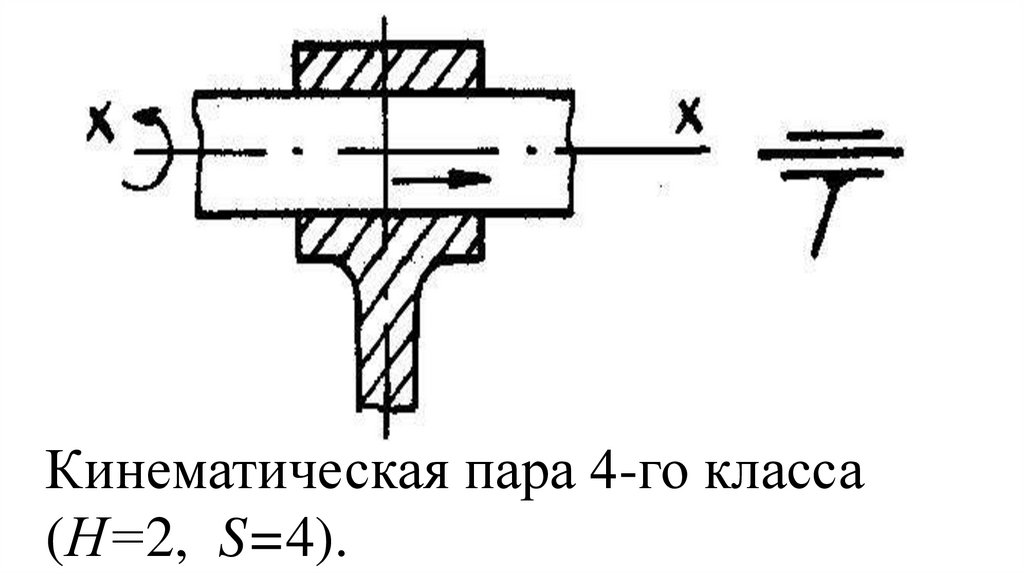
Кинематическая пара 4-го класса(Н=2, S=4).
54.
Наибольшее распространениеполучили кинематические пары 5-го
класса (одноподвижные), и к ним
относятся поступательная,
вращательная и винтовая пары.
55.
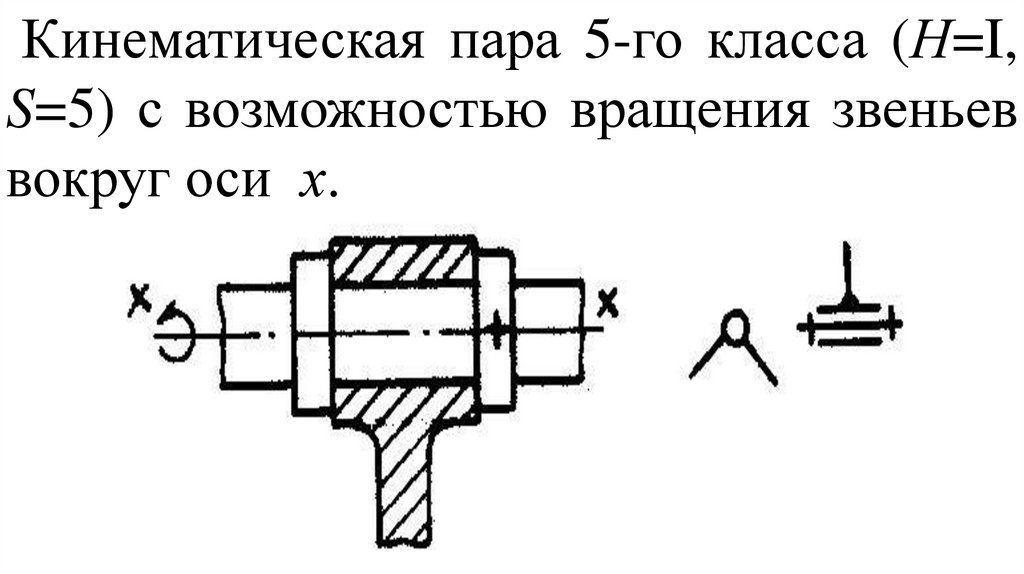
Кинематическая пара 5-го класса (Н=I,S=5) с возможностью вращения звеньев
вокруг оси х.
56.
Пары 5-го класса(Н=1, S=5) с
возможностью
поступательного
движения одного
звена относительно
другого вдоль оси
х.
57.
Если в кинематической паре имеются двафункционально связанных движения (одно
без другого существовать не может), то они
дают одну степень свободы.
Например, неподвижный болт с гайкой
составляют кинематическую пару пятого
класса, так как гайка вращаясь вокруг оси
болта поступательно движется вдоль этой
оси.
58.
Кинематические пары разделяют нанизшие и высшие. Кинематическая
пара, у которой соединение двух
звеньев происходит по поверхности,
называется низшей.
Это пары – поступательные,
вращательные, сферические,
винтовые и плоскостные.
59.
Соединение двух звеньев по линии илиточке образует высшую кинематическую
пару. К высшим кинематическим парам
относятся пары «шар на плоскости» и
«цилиндр на плоскости». Например,
колесо и рельс, фрикционные катки,
кулачковые пары и другие.
60.
Низшие пары способны передаватьзначительные усилия при меньшем
износе в сравнении с высшими
кинематическими парами, так как сила
давления одного звена на другое звено у
них распределяется по площади
поверхности соприкосновения.
61.
У высших пар соприкосновениезвеньев происходит в точках или по
линиям. В зоне контакта звеньев
возникают большие напряжения.
К достоинствам высших пар можно
отнести возможность воспроизводить с
их помощью достаточно сложные
относительные движения.
62.
1.6 Кинематические цепиКинематической цепью называют
систему звеньев, связанных между
собой кинематическими парами. Если
звенья совершают движение в одной
плоскости, то кинематическая цепь
плоская, в противном случае пространственная.
63.
В зависимости от строениякинематическая цепь может быть простой и
сложной, замкнутой и разомкнутой.
К простым цепям относят кинематические
цепи, у которых каждое звено входит в две
кинематические пары.
64.
65.
К сложным относят кинематическиецепи, имеющие звенья, входящие в
состав трех и более кинематических
пар, т. е. содержит хотя бы одно звено с
тремя или более вершинами (звено 2).
66.
67.
Механизмы могут быть образованыкак замкнутыми, так и незамкнутыми
кинематическими цепями.
К замкнутым цепям относятся цепи,
у которых каждое звено входит, по
крайней мере, в две кинематические
пары (рис. 4).
68.
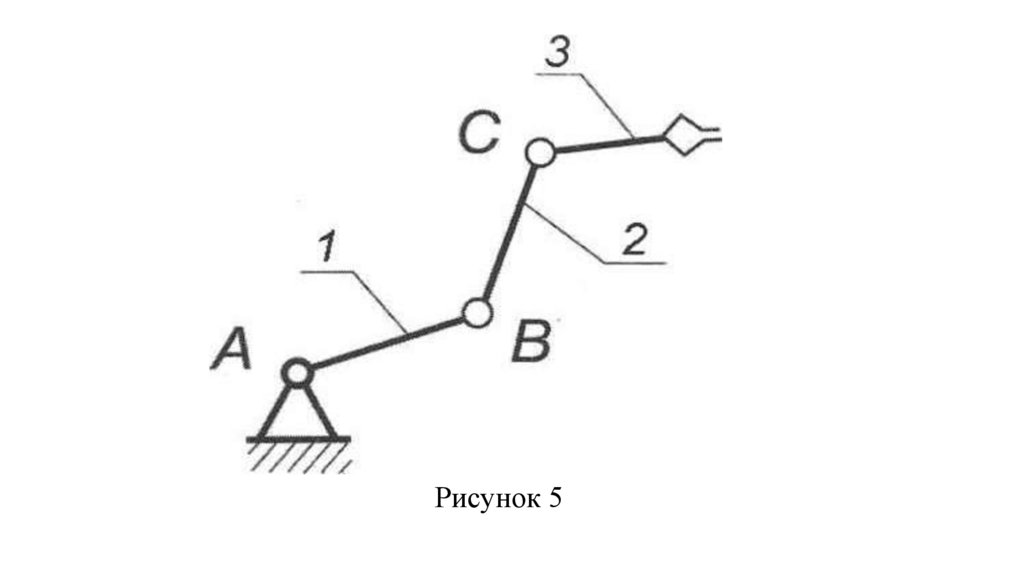
Рисунок 469.
К незамкнутым цепям относятся цепиу которых есть звенья (звено 3),
входящие только в одну
кинематическую пару (рис. 5).
70.
Рисунок 571.
Подвижные звенья плоскойкинематической цепи совершают
движения в одной неподвижной
плоскости (см. рис. 1, 3, 5).
72.
В пространственных кинематическихцепях точки звеньев описывают
пространственные кривые, либо
движутся по плоским кривым, лежащим
в пересекающихся плоскостях (рис. 4).
73.
1.7 Основные виды механизмовИзвестны шарнирно-рычажные,
фрикционные, зубчатые, мальтийские,
храповые, кулачковые, винтовые
механизмы, механизмы с гибкими звеньями,
с неполными зубчатыми колесами и другие,
имеющие различные кинематические,
конструктивные и функциональные свойства.
74.
Шарнирно-рычажные механизмыприменяются для преобразования
вращательного или поступательного
движения входного звена во
вращательное или поступательное
движение выходного звена с
требуемыми параметрами.
75.
Например, плоский четырехзвенник стремя подвижными звеньями и одним
неподвижным, служит для
преобразования равномерного
вращательного движения ведущего
звена 1 в неравномерное вращательное
движение звена 3 (см. рис. 1).
76.
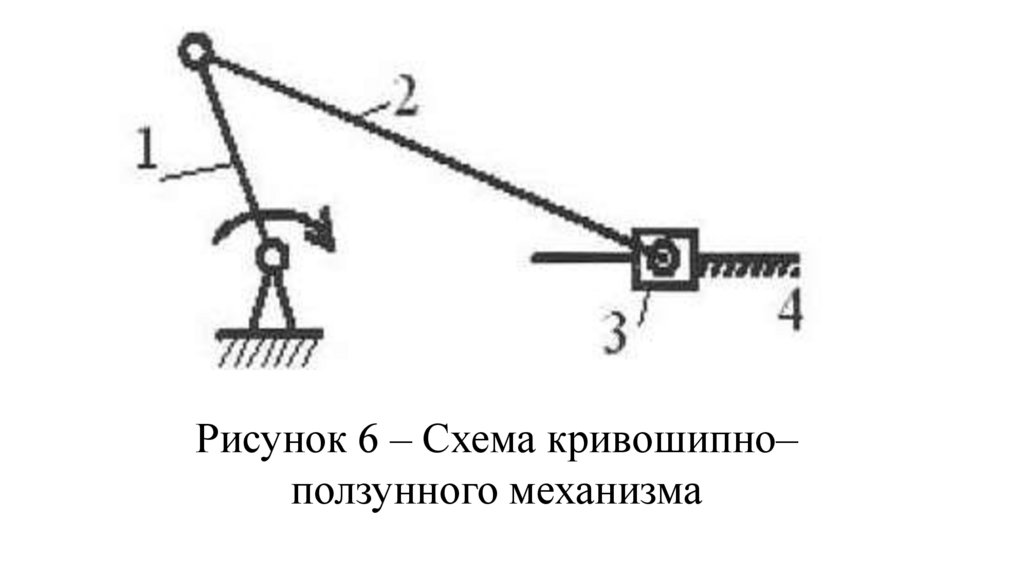
Кривошипно-ползунные механизмы(рис. 6), применяются для
преобразования вращательного движения кривошипа 1 в поступательное
движение ползуна 3 и наоборот.
77.
Рисунок 6 – Схема кривошипно–ползунного механизма
78.
Особенностью кулисных механизмовявляется наличие ползуна (камня),
перемещающегося относительно
подвижной направляющей – кулисы 3
(рис. 7), которая в зависимости от
соотношения размеров звеньев может
совершать вращательные или
качательные движения.
79.
Рисунок 7 – Схемакулисного механизма
80.
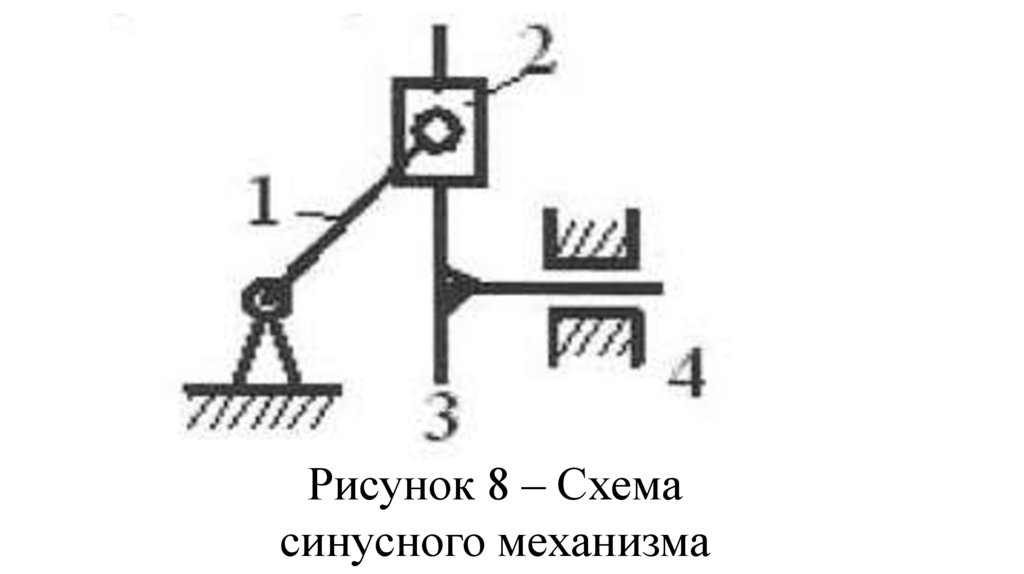
Разновидностью кулисного механизмаявляется синусный механизм (рис. 8), с
помощью которого преобразуется
вращательное движение звена 1 в
возвратно-поступательное движение
кулисы 3. При этом перемещение
кулисы 3 пропорционально синусу угла
поворота звена 1.
81.
Рисунок 8 – Схемасинусного механизма
82.
Принцип действия фрикционныхмеханизмов основан на передаче движение
от ведущих звеньев к ведомым за счет сил
трения. Силы трения возникают в месте
контакта звеньев под воздействием сил
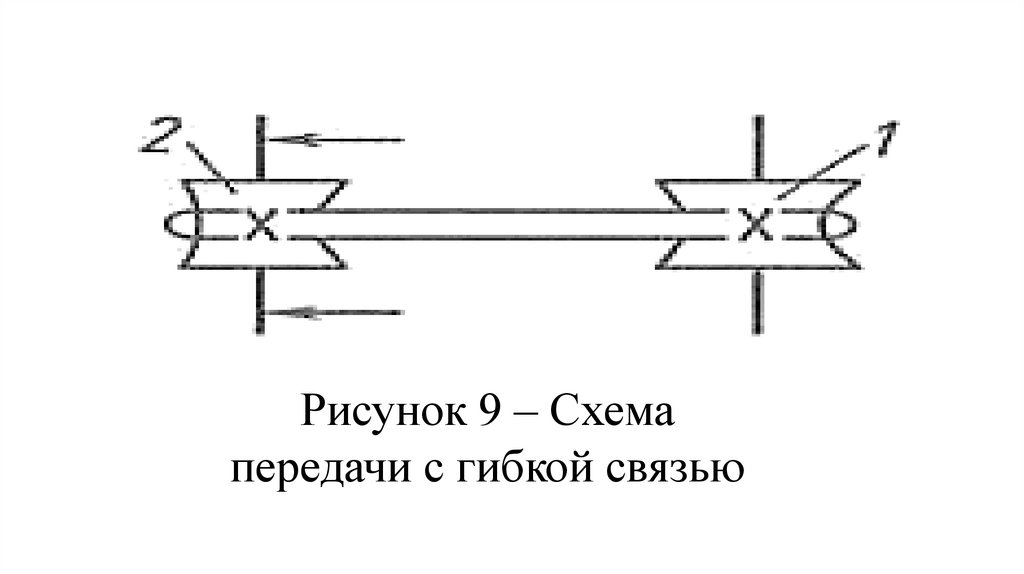
прижимающих звенья друг к другу.
Различают фрикционные передачи с
гибкими и твердыми звеньями.
83.
В передачах с гибкими связямивращательное движение ведущего звена
(шкива) 2 передаётся ведомому звену
(шкиву) 1 за счет сил трения между
гибкой связью (ремнём) и шкивами
(рис. 9).
84.
Рисунок 9 – Схемапередачи с гибкой связью
85.
На рисунке 10 показаныкинематические схемы фрикционных
передач с постоянным передаточным
отношением. Вращательное движение
ведущих катков 1 передается ведомым
каткам 2 благодаря силе трения,
возникающей в месте контакта катков.
86.
Рисунок 10 – Схемы фрикционных передач:а) цилиндрическая, б) коническая
87.
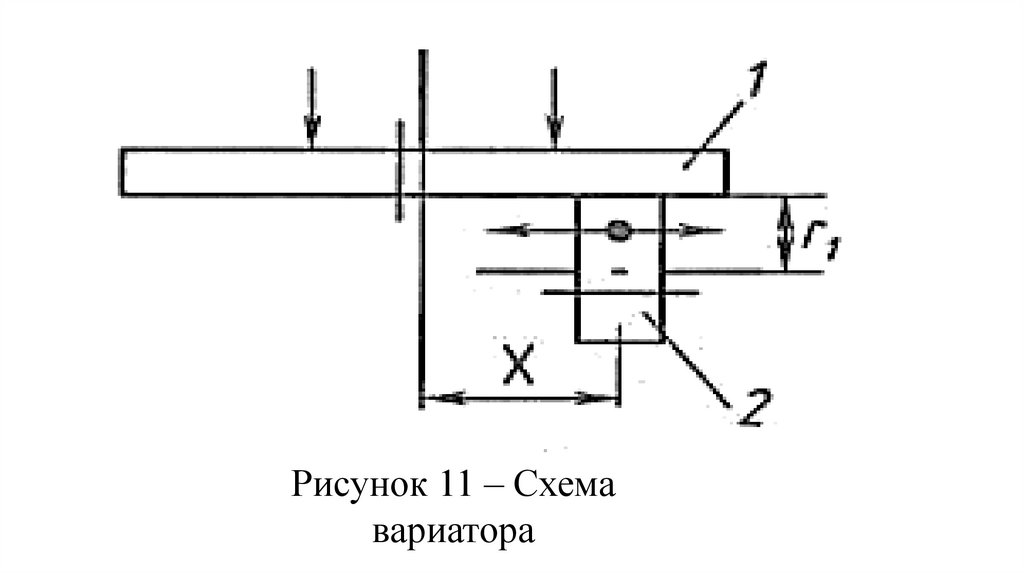
Кинематическая схема передачи спеременным передаточным отношением
(вариатора) представлена на рис. 11.
Ведущий каток 2 может перемещаться
относительно ведомого катка 1. При
этом изменение расстояния Х приводит
к изменению передаточного отношения
вариатора.
88.
Рисунок 11 – Схемавариатора
89.
Фрикционные передачи также служатдля преобразования вращательного
движения ведущего звена в
прямолинейное движение ведомого
звена (рис. 12).
90.
а)Рисунок 12– Схема передачи с
прямолинейным движением ведомого звена
91.
К достоинствам фрикционныхмеханизмов относятся простота конструкции, автоматическое предохранение
от поломок при перегрузках, плавность
передачи движения.
92.
К недостаткам фрикционныхмеханизмов следует отнести
непостоянство передаточного
отношения из-за проскальзывания
звеньев. Кроме того, наличие усилия,
прижимающего катки друг к другу,
приводит значительному износу звеньев.
93.
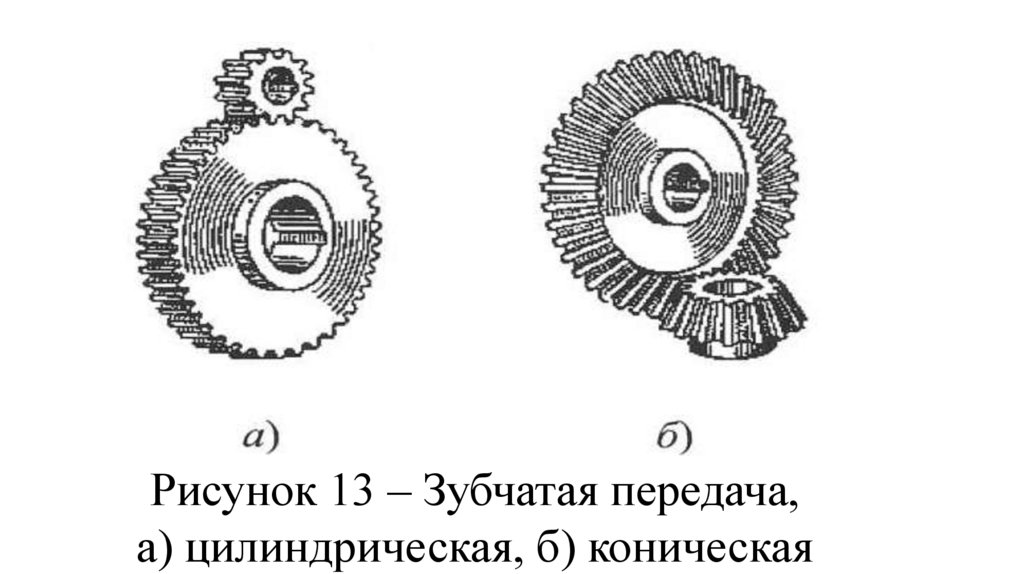
Зубчатые механизмы (передачи)служат для изменения скорости
вращательного движения зубчатых
колёс, преобразования вращательного
движения в поступательное и наоборот.
Передача движения осуществляется
зацеплением зубьев подвижных звеньев
– зубчатых колес (рис. 13).
94.
Рисунок 13 – Зубчатая передача,а) цилиндрическая, б) коническая
95.
Одноступенчатый зубчатый механизмсостоит из стойки и двух подвижных
звеньев – зубчатых колес. Колеса
образуют друг с другом – высшую
кинематическую пару 4-го класса,
называемую зубчатым зацеплением.
96.
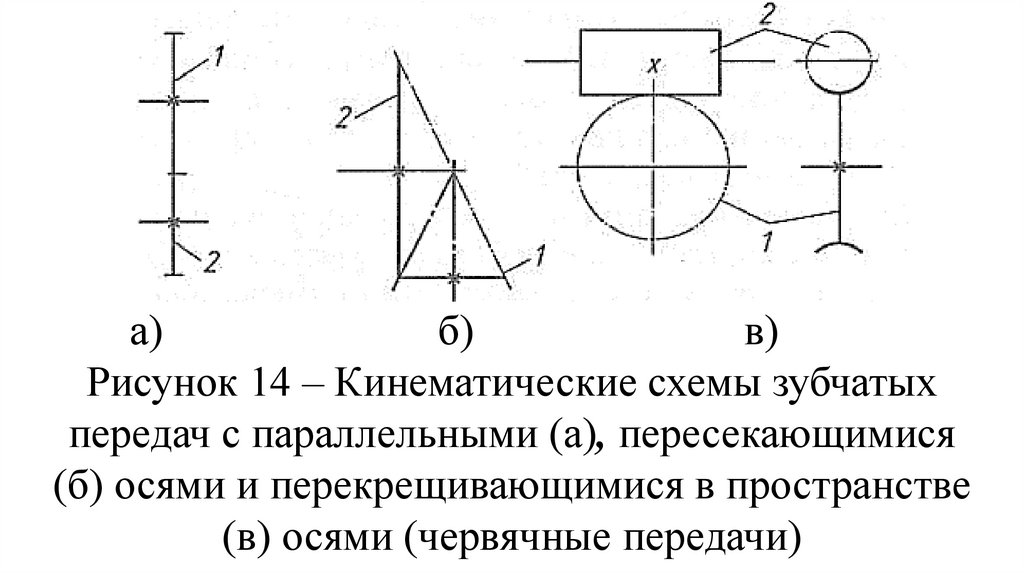
а)б)
в)
Рисунок 14 – Кинематические схемы зубчатых
передач с параллельными (а), пересекающимися
(б) осями и перекрещивающимися в пространстве
(в) осями (червячные передачи)
97.
Различают передачи с внешним (рис.1.14) и внутренним (рис. 1.15)
зацеплением. При внешнем зацеплении
колеса с параллельными осями
вращаются в разные стороны, при
внутреннем – в одну.
98.
Рисунок 15 – Кинематическая схема зубчатой передачи свнутренним зацеплением
99.
Кинематическая схема зубчатогомеханизма (передачи) для
преобразования вращательного
движения зубчатого колеса 1 в
поступательное движения зубчатой
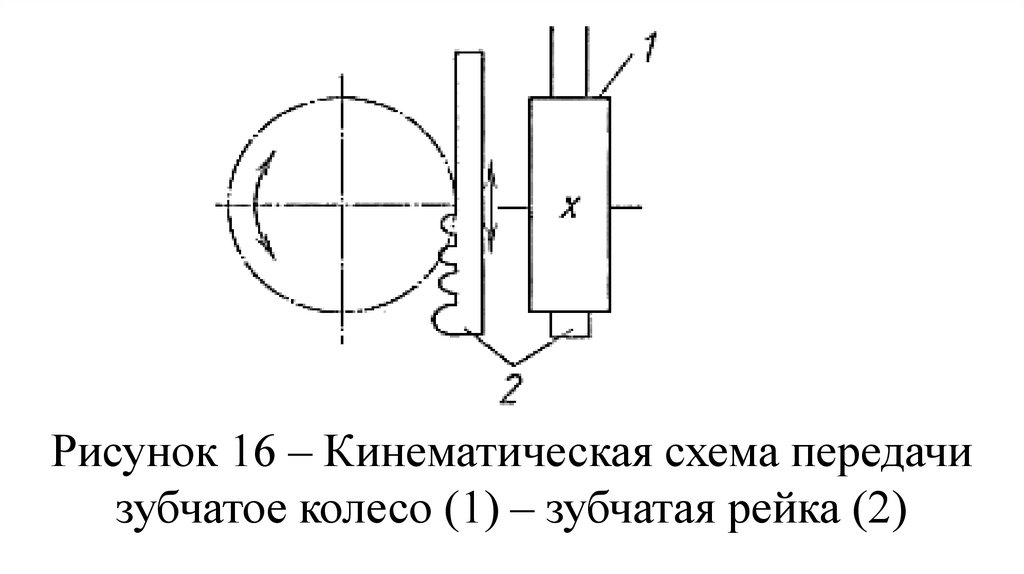
рейки 2 показана на рис. 16.
100.
Рисунок 16 – Кинематическая схема передачизубчатое колесо (1) – зубчатая рейка (2)
101.
Кулачковые механизмы (рис 1.8, 1.9)позволяют получать любой закон
движения ведомого звена. Ведущее
звено кулачкового механизмы –кулачок,
который образует с толкателем высшую
кинематическую пару 4-го класса.
102.
С помощью кулачковых механизмовможно вращательное движение кулачка
1 преобразовывать в возвратно-поступательное или качательное движение
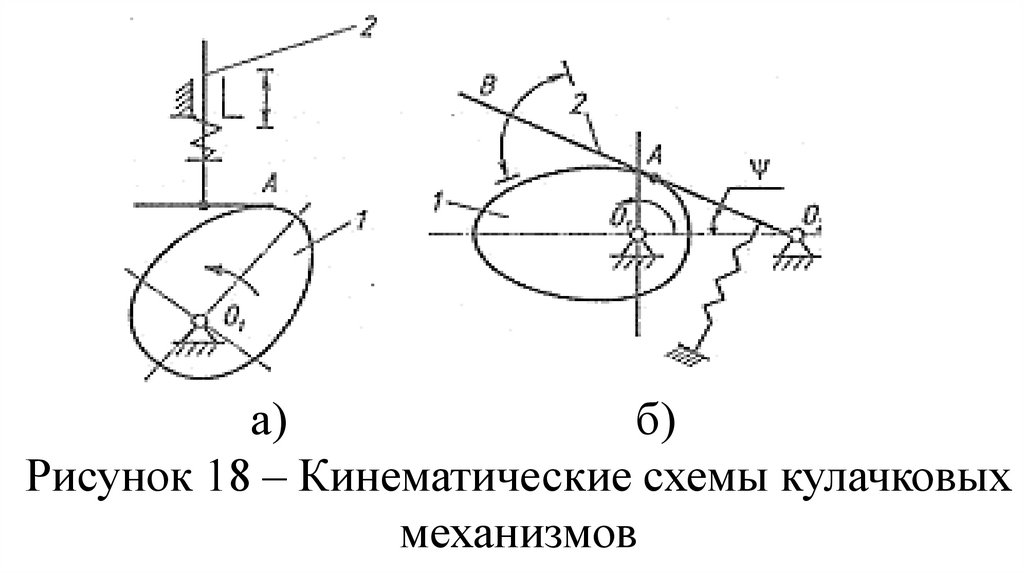
толкателя 2 (рис. 18).
103.
а)б)
Рисунок 18 – Кинематические схемы кулачковых
механизмов
104.
Рисунок 19 – Кинематические схемы механизмовс возвратно-поступательным движением кулачка
105.
К недостаткам кулачковых механизмовследует отнести большие удельные
давления в высшей кинематической
паре что снижает долговечность
механизма, а также необходимость в
силовом замыкании звеньев.
106.
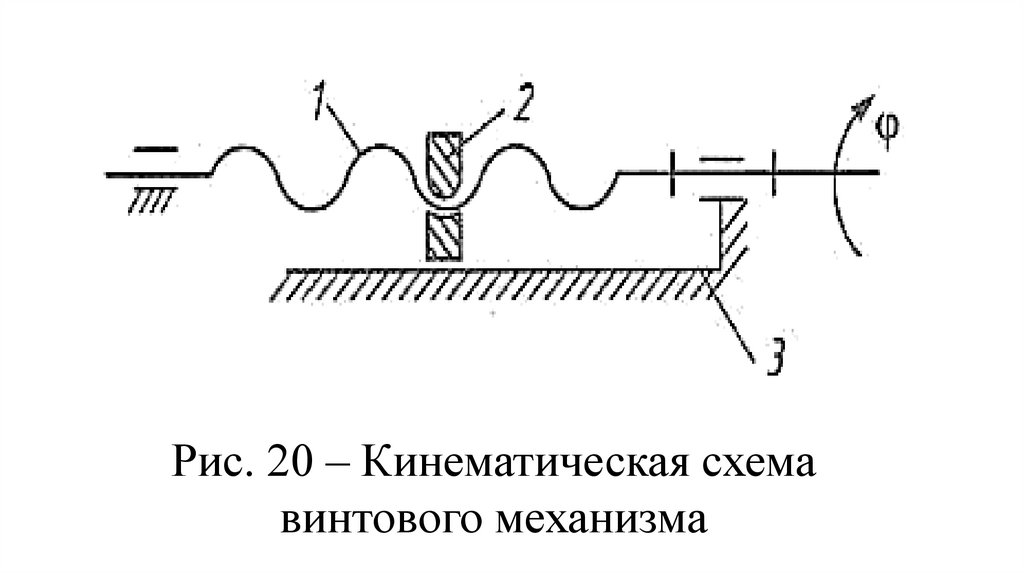
Винтовые механизмы предназначеныдля преобразования вращательного
движения винта в прямолинейное
движение гайки и наоборот. При
вращении винта 1 (рис. 20) гайка 2
поступательно перемещается в
направляющих стойки 3.
107.
Рис. 20 – Кинематическая схемавинтового механизма
108.
Если ведущим звеном являетсязафиксированная в осевом направлении
вращающаяся гайка, то винт движется
поступательно в направляющих стойки.
Винтовые механизмы обеспечивают
высокую точность поступательных
перемещений и большой выигрыш в
силе.
109.
Недостатки винтовых механизмов –большие потери на трение в паре винтгайка, низкий КПД.
Применяются в измерительных
приборах, механизмах точных
перемещений, в подъемнотранспортных устройствах.
110.
Механизмы с гибкими звеньямиприменяют для передачи вращательного
движения при больших межосевых
расстояниях между валами. Условием
нормальной работы передачи трением
является натяжение гибкого звена.
111.
Ведущее и ведомое жесткие звеньятаких механизмов непосредственно не
контактируют друг с другом.
Механизмы с гибкими звеньями
подразделяют на передачи трением и
передачи зацеплением.
112.
В передачах трением в качестве гибкогозвена используют плоские и
клиновидные ремни (рис. 21).
113.
Рис. 21 – Кинематическая схема передачитрением с гибким звеном:
1, 2 – шкивы, 3 – ремень, 4 - натяжной механизм
114.
В передачах зацепления гибкимзвеном служит зубчатый ремень,
перфорированная лента, цепь.
Преимущества этих передач перед
передачами трением соответствуют
преимуществам зубчатых передач по
сравнению с фрикционными.
115.
Механизмы прерывистого движенияприменяют в устройствах требующих
прерывистости движения ведомого
звена. Для получения такого движения
кроме кулачковых механизмов
применяют мальтийские и храповые
механизмы, а также механизмы с
неполными зубчатыми колесами.
116.
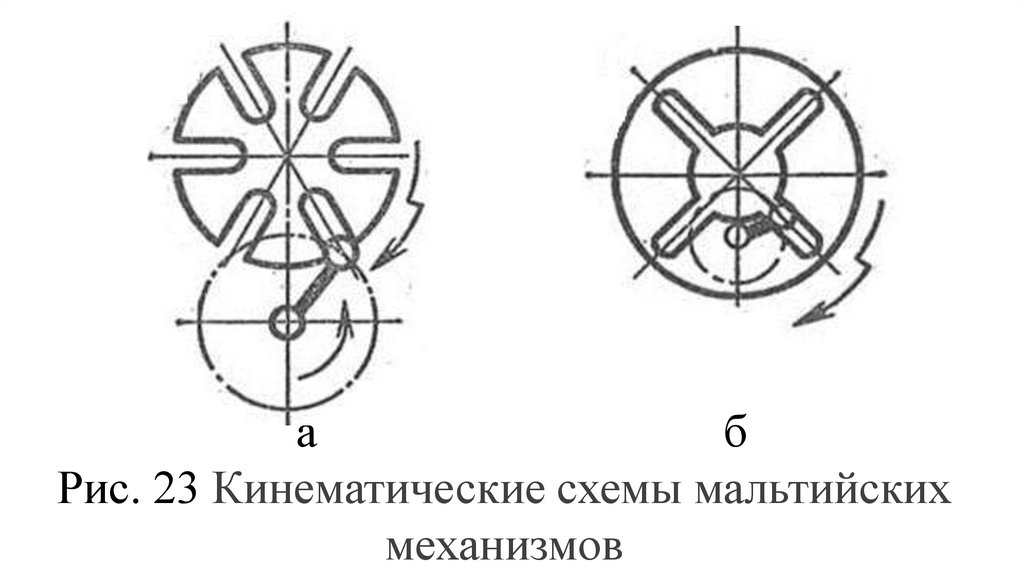
Мальтийские механизмы в сочетании сзубчатыми передачами используют для
прерывистого движения ленточных
транспортеров, в многопозиционных
устройствах (автоматах и т.д.).
Различают два типа мальтийских
механизмов: с внешним зацеплением
(рис. 23, а) и внутренним (рис. 23,б).
117.
аб
Рис. 23 Кинематические схемы мальтийских
механизмов
118.
При вращении кривошипа (рис. 23, а)его палец (цевка) входит в паз креста и,
поворачивает крест на определенный
угол, после чего выходит из прорези.
Ведомый крест остается неподвижным
до тех пор пока цевка кривошипа опять
войдёт в следующий паз креста.
119.
На кривошипе может быть несколькоцевок, что позволяет получать равные и
неравные интервалы перемещений и
остановов за один оборот ведущего
звена.
В механизме с внутренним
зацеплением (рис. 23, б) кривошип и
крест вращаются в одном направлении.
120.
Механизмы с внутреннимзацеплением являются конструктивно
более сложными, но имеют меньшие
габаритные размеры и меньшие
угловые ускорения креста, т.е. меньшие
динамические нагрузки.
121.
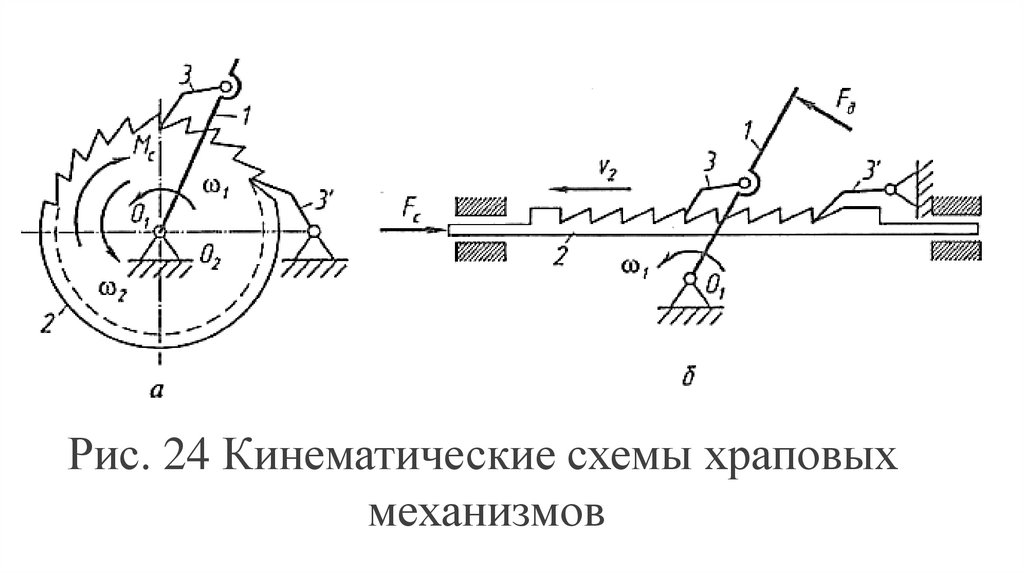
Храповый механизм (рис. 24) состоитиз ведущего звена 1, ведомого звена 2
(храпового колеса или храповой рейки)
с зубьями специального профиля и
неподвижного звена (стойки).
122.
Рис. 24 Кинематические схемы храповыхмеханизмов
123.
Качательное движение от ведущегозвена 1 к ведомому 2 передается с
помощью собачки 3, которая при
движении ведущего звена в рабочем
направлении упирается в зуб ведомого
звена и перемещает его.
124.
При возвращении ведущего звена 1 исобачки 3 в исходное положение
храповое колесо (рейка) 2 стопорится
собачкой 3’ и остается неподвижным.
Зацепление собачки с ведомым звеном
может быть внешним и внутренним.
125.
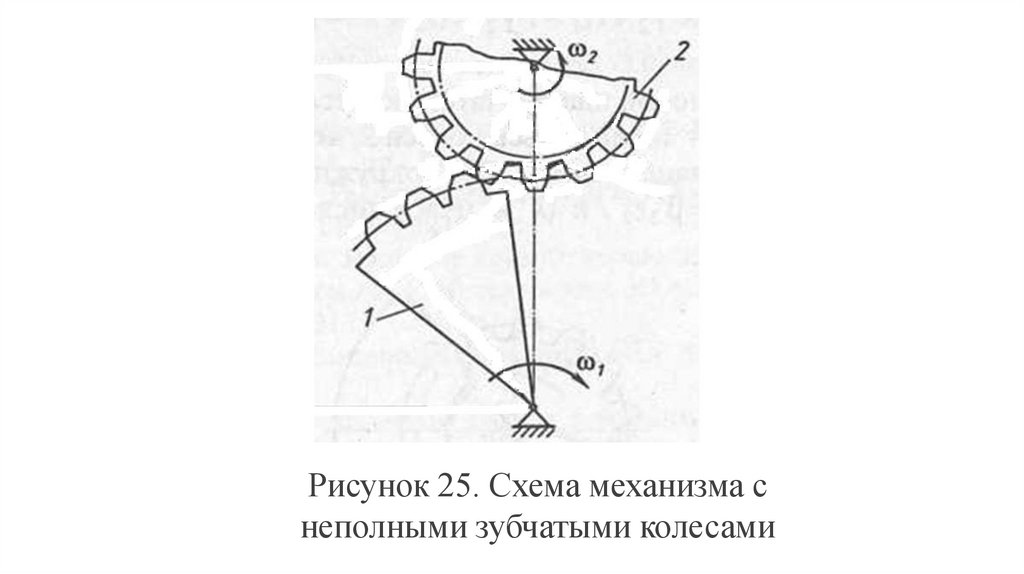
Механизм с неполными зубчатымиколесами состоит из ведущего звена –
зубчатого сектора 1 – и ведомого
зубчатого колеса 2 (рис. 25).
Зубчатые механизмы прерывистого
действия применяют в устройствах
прерывистого перемещения.
126.
Рисунок 25. Схема механизма снеполными зубчатыми колесами
127.
Зубчатые механизмы по сравнению смальтийскими имеют более широкие
пределы соотношения времени
движения и покоя, углов поворота
ведущего и ведомого колес.
Недостатком механизма является
наличие жесткого удара в момент
начала движения.
128.
2 Структурный анализ механизмовПод структурным анализом
механизма понимается определение
количества звеньев и кинематических
пар, определение степени подвижности
и установление класса и порядка
механизма.
129.
Степенью подвижности механизмасчитается число степеней свободы W
относительно стойки.
Степень подвижности W плоского
механизма определяется по формуле
Чебышева:
где n - число подвижных звеньев, Рн и
Рв - число низших и высших
кинематических пар.
130.
Степень подвижностипространственного механизма
определяется по формуле СомоваМалышева:
где P1, Р2, Рз, Р4, Р5 – число одно-,
двух-, трех-, четырех- и пяти
подвижных кинематических пар.
131.
Построение механизма по Ассурусостоит в присоединении ведущего
(начального) звена к стойке и затем в
последовательном присоединении к
ведущему звену структурных групп
Ассура, без изменения степени
подвижности механизма в целом.
132.
Группа Ассура – это кинематическаяцепь с нулевой степенью подвижности
относительно тех звеньев, к которым
она присоединяется своими элементами.
Такая цепь не распадается на еще более
простые кинематические цепи.
133.
Структурные группы характеризуютсяклассом и порядком. Класс группы
определяется числом кинематических
пар наиболее сложного контура.
Порядок определяется числом
свободных элементов кинематических
пар, которыми группа присоединяется к
другим звеньям.
134.
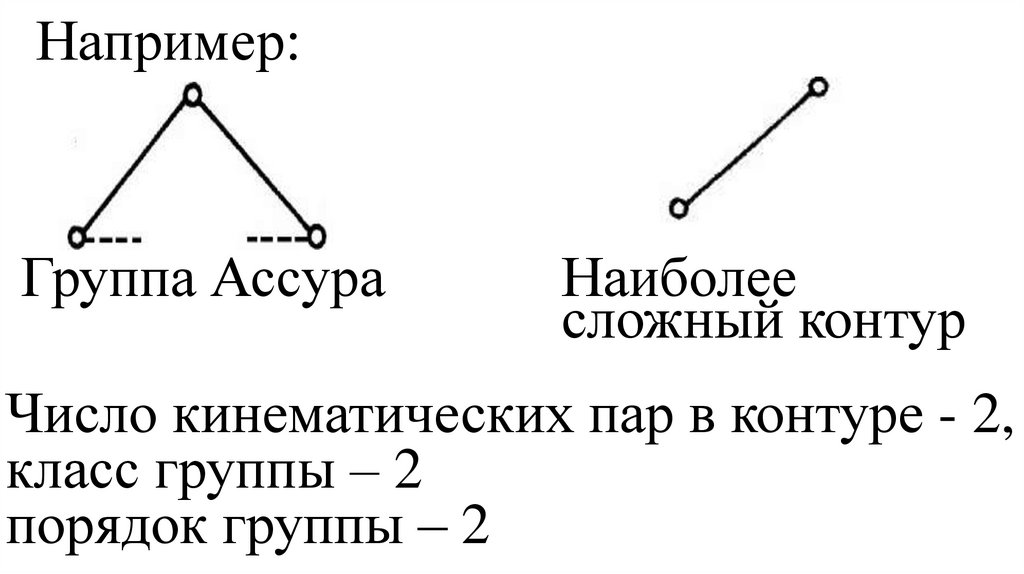
Например:Группа Ассура
Наиболее
сложный контур
Число кинематических пар в контуре - 2,
класс группы – 2
порядок группы – 2
135.
Например:Группа Ассура
Наиболее
сложный контур
Число кинематических пар в контуре – 3,
класс группы – 3,
порядок группы – 3.
136.
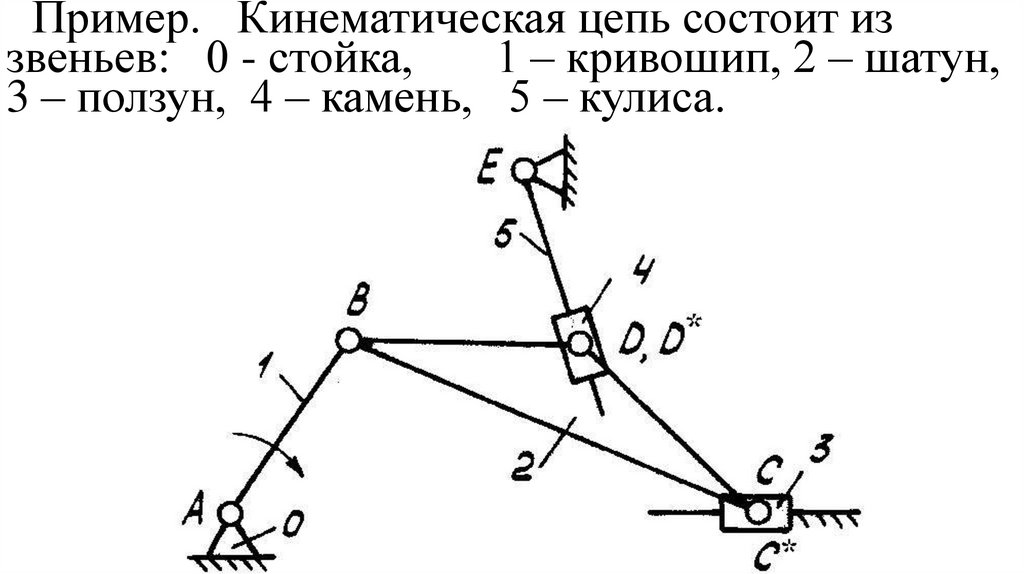
Пример. Кинематическая цепь состоит иззвеньев: 0 - стойка,
1 – кривошип, 2 – шатун,
3 – ползун, 4 – камень, 5 – кулиса.
137.
Кинематические пары образованызвеньями:
А (0-1) - 5 кл.- вращательная, низшая;
В (1-2) - 5 кл.- вращательная, низшая;
С (2-3) - 5 кл. - вращательная, низшая;
С* (3-0) - 5 кл. - поступательная, низшая;
D (2-4) - 5 кл. - вращательная, низшая;
138.
D* (4-5) - 5 кл. - поступательная,низшая;
Е (5-0) - 5кл. - вращательная, низшая.
Точки С* и D* - точки принадлежащие
разным звеньям, но совпадающие с
точками С и D соответственно.
139.
Степень подвижности вычисляется поформуле Чебышева
W = 3n − 2p5 − p4 = 3⋅5 − 2⋅7 −0 = 1.
Степень подвижности совпадает с
числом начальных звеньев (по заданию
звено 1 - начальное). Поэтому заданная
кинематическая цепь является
механизмом.
140.
При проведении структурного анализаструктурные группы следует выделять,
начиная с группы наиболее удаленной от
начального звена.
Структурная группа 4-5:
W = 3n − 2p5 = 3⋅2 − 2⋅3 = 0.
Группа 2-го класса, 2-го
порядка, 3-го вида.
141.
Структурная группа 2-3:W = 3n − 2p5 = 3⋅2 − 2⋅3 = 0,
Группа 2-го класса, 2-го порядка, 2-го
вида.
142.
Оставшаяся частьявляется начальным звеном:
W = 3n − 2p5 = 3⋅1− 2⋅1= 1.
Рассмотренный в этом
примере механизм является
механизмом 2-го класса, т.к.
структурных групп выше
2-го класса нет.
143.
2.3. Синтез рычажныхмеханизмов
Синтез механизмов выполняется в два
этапа. Первый этап называется
структурным синтезом, а второй –
метрическим синтезом.
144.
Структурный синтез – это процесспроектирования структуры нового или
модернизация структуры уже
существующего механизма.
145.
На этапе структурного синтезаосуществляется формирование
структурной схемы механизма, которая
определяет число звеньев, количество,
вид и подвижность кинематических пар
146.
В то же время определяющимиусловиями являются: заданный закон
движения и расположение осей
входного и выходного звеньев.
147.
Структурный синтез плоскихрычажных механизмов выполняется в
соответствии со структурной
классификацией Ассура Л.В.
В качестве примера рассмотрим
структурный синтез кривошипноползунного механизма.
148.
К выбранному первичному механизму(рис. 2.6, а) присоединяем структурную
группу звеньев 2-го класса 2-го порядка
2-го вида (рис. 2.6, б).
Полученный таким образом механизм
будет обладать подвижностью равной
единице.
149.
Рис. 2.6. Схема структурного синтезакривошипно-ползунного механизма
150.
Метрический синтез – это процессопределения основных геометрических
размеров звеньев механизма и
конфигураций профилей рабочих
поверхностей, которые наилучшим
образом удовлетворяют заданным
условиям и обеспечивают оптимальное
сочетание качественных показателей.
151.
Результатом синтеза являетсякинематическая схема механизма.
Кинематическая схема – это
графическое изображение механизма,
выполненное с учётом масштабного
коэффициента длины с использованием
условных обозначений,
рекомендованных ГОСТ.
152.
Масштабный коэффициент длины –это отношение действительной
величины длины звена l, взятой в
метрах, к длине отрезка ⏐l⏐,
измеряемого в миллиметрах и
изображающего эту величину в составе
кинематической схемы.
153.
Значения масштабного коэффициентапринимаются произвольно в
зависимости от заданных условий и
целей решения требуемых задач.
154.
3 Кинематический анализ плоскихрычажных механизмов
3.1 Задачи и методы кинематического
анализа
155.
Задачами кинематического анализамеханизма являются:
а) определение положений звеньев и
построение траекторий точек;
б) определение линейных скоростей и
ускорений точек звеньев механизма;
в) определение угловых скоростей и
ускорений звеньев механизма.
156.
С целью проведения кинематическогоанализа механизмов используют
различные методы:
а) графический - наглядный, но
неточный;
б) графоаналитический - наглядный и
достаточно точный;
157.
в) аналитический - более точный, чемпредыдущие, однако не обладает
наглядностью и достаточно трудоемкий;
г) экспериментальный - не требует
допущений, предполагаемых в трех
предыдущих методах, но требует
наличия реального механизма и
измерительной аппаратуры, обладает
большой трудоёмкостью.
158.
3.2 Графический методАнализ начинается с построения
совмещенных планов механизма,
выполненных в одной системе
координат для ряда последовательных
последовательных положений
начального звена с учетом принятого
масштабного коэффициента длины.
159.
На рис. 3.1 показаны совмещенныевосемь планов кривошипноползунного механизма выполненные с
учётом масштабного коэффициента
µl = lAB / AB , (м/мм).
160.
161.
На рис. 2.2, а построена диаграммаперемещений точки С в зависимости от
времени (t). По оси абсцисс отложено время.
Масштабный коэффициент времени принят
µt = T / lT (с/мм), где T - время одного
оборота кривошипа, a lT - отрезок в мм,
изображающий это время. По оси ординат
отложено перемещение точки С. В данном
случае принято µS = µl .
162.
163.
Диаграмму скоростей Vc в зависимости отвремени (t) получают методом графического
дифференцирования диаграммы перемещений
точки С методом хорд. Для этого на каждом
участке кривую Sc заменяют хордой, т.е.
неравномерное движение приближенно заменяют
равномерным. Для этого, выбрав произвольно
полюсное расстояние Н1, из точки Р1 проводят
лучи, параллельные хордам на кривой Sc.
164.
165.
Отрезки на оси ординат, отсекаемые этимилучами, показывают постоянные скорости на
соответствующих участках. Затем проводят
плавную кривую таким образом, чтобы площади
фигур, расположенных с обеих сторон кривой, на
каждом участке были одинаковы.
Для построения диаграммы ускорений ac
аналогичным образом графически
дифференцируют функцию диаграмму Vc .
166.
При вычислении скоростейи ускорений нужно
учитывать масштабные
коэффициенты которые
определяются по формулам:
167.
3.3. Графоаналитический методГрафоаналитический метод
кинематического анализа механизмов
предполагает аналитическую запись
векторных уравнений и графическое их
решение с помощью построения планов
скоростей и ускорений.
168.
Планом скоростей (ускорений)называется фигура, составленная из
векторов абсолютных скоростей
(ускорений) точек звеньев, выходящих
из одной точки, называемой полюсом
плана скоростей (ускорений), и векторов
относительным скоростей (ускорений),
соединяющих концы векторов
абсолютных скоростей (ускорений).
169.
Методику выполнениякинематического анализа механизма
графоаналитическим методом
рассмотрим на примере анализа
плоского шарнирного механизма,
ведущее звено которого вращается с
постоянной угловой скоростью ω1
(рис.2.8).
170.
Рисунок 2.8 – План механизма171.
Механизм состоит из ведущего звена1 (кривошипа), группы Ассура 2-го
класса, состоящей из звеньев 2 (шатуна)
и 3 (коромысла), а также группы Ассура
2-го класса, состоящей из звеньев 4
(шатуна) и 5 (ползуна).
172.
Данный механизм предназначендля преобразования равномерного
вращательного движения
кривошипа 1 в возвратнопоступательное движение ползуна
5.
173.
Механизм имеет одну степеньподвижности. За обобщенную
координату принимается заданный
угол φ1.
174.
Выполнение кинематическогои кинетостатического анализов
начинается с построения
совмещенных планов механизма
в нескольких положениях входного
звена, например, шести.
175.
Планы положения механизма строят сучётом масштабного коэффициента
длины µl (м/мм) под которым
понимают отношение изображаемой на
чертеже величины длины звена lAB к
соответствующему отрезку чертежа.
где lАВ - длина звена 1, м; АВ - отрезок,
изображающий звено 1 на чертеже, мм.
176.
177.
Под кинематическим анализомподразумевается определение угловых
скоростей и ускорений звеньев 2, 3, 4, а
также скоростей и ускорений
характерных точек В, С, Е и F звеньев
механизма при заданной угловой
скорости ведущего звена ω1 в каждом из
шести положение механизма.
178.
В учебных целях методикавыполнения построений планов сил
показана только для одного, например,
пятого положения механизма.
179.
Построение плана скоростейp
начинается с построения полюса v
в непосредственной близости с планом
механизма. Точки A и D механизма
неподвижны. Их скорости равны нулю.
Поэтому точки a и d также находятся в
полюсе.
180.
181.
Скорость точки В ведущего звена VB (м/с)и масштабный коэффициент скорости µv
-1
(м·с /мм) определяются по формулам:
где (рvb) - длина отрезка, изображающего
скорость VB на плане скоростей (выбирается
максимально возможным для имеющегося
места построения плана скоростей).
182.
Точка С принадлежит одновременно звену2 и звену 3. Абсолютную скорость точки С
можно представить суммой скоростей
переносного и относительного движений.
Переносным движением является
поступательное движение звена 2 со
скоростью точки В (VB), а относительным вращательное движение этого звена вокруг
точки В (VСB).
183.
Поэтому на основании теоремы «Осложении скоростей», вектор скорости
точки С можно
определить
из
векторных
уравнений VC VB VCB и VC VD VCD .
VCB и VCD - векторы скорости точки С
во вращательном движении звена 3
относительно точек B и D.
.
184.
При определении направлений векторов наплане скоростей руководствуются
следующими правилами:
вектор абсолютной скорости всегда
направлен из полюса;
вектор относительной скорости всегда
направлен к точке плана,
соответствующей первой букве индекса в
обозначении этой скорости.
185.
Для построения плана скоростей изполюса рv откладывают отрезок (рv b).
Отрезок направлен перпендикулярно
звену АВ в сторону, соответствующую
направлению вращения звена АВ.
186.
187.
Затем из точки b проводят линиюперпендикулярно звену СВ.
VD = 0, конец вектора vD (точка d на плане
скоростей) совпадает с полюсом рv. Из точки d
проводят линию действия вектора, направленную
перпендикулярно звену CD. Точка с на
пересечении построенных линий определяет
положение конца вектора скорости VC. Вектор
скорости VCВ на плане скоростей – отрезок cb.
188.
189.
Положение точки е на планескоростей определяется на основании
теоремы подобия из пропорции
p v e l DE
.
p v c l CD
.
190.
Составляется векторное уравнениеУравнение решается графически.
Ускорение точки F – вектор рv f на
плане скоростей.
191.
192.
Значенияискомых
скоростей,
например VCВ и VCD , находятся путем
измерения длин отрезков cb и cd на
плане скоростей и умножением их на µv .
Полученные результаты
используются при определении угловых
скоростей звеньев механизма.
193.
Модуль угловой скорости вращениязвена 2 (шатуна) подсчитывается по
формуле:
Мысленный перенос вектора VCD с
плана скоростей в точку С на плане
механизма позволяет установить, что
угловая скорость ω3 звена 3 направлена,
так как и ω2 шатуна 2.
194.
На схеме механизма направленияугловых скоростей звеньев указывают
круговыми стрелками.
Построение плана скоростей
позволяет определить скорости любых
точек механизма.
195.
Для определения ускорений точекзвеньев механизма строят план
ускорений при заданном значении
обобщенной координаты φ1. Точка В
движется с постоянной угловой
скоростью по окружности и её
2
ускорение равно a B 1 l AB .
196.
Построение плана ускоренийначинается с отображения полюса pα в
непосредственной близости с планом
механизма. Точки A и D на плане
механизма неподвижны. Их ускорения
равны нулю, поэтому точки a и d также
находятся в полюсе
.
197.
Масштабный коэффициент ускорениявыбирается произвольно.
На плане ускорений вектор ускорения
точки В параллелен кривошипу АВ и
направлен из полюса в направлении от
точки В к точке А на плане механизма.
pa
198.
199.
Точка С одновременно принадлежитшатуну ВС и коромыслу CD. На
основании теоремы «О сложении
ускорений», можно записать следующие
векторные уравнения для определения
ускорения точки С:
200.
nac aB aCB aCB ;
n
ac a D aCD aCD .
Модули нормальных составляющих
относительных ускорений равны:
201.
nn
a B aCB aCB aCD aCD .
202.
nn
a B aCB aCB aCD aCD .
203.
Для определения положения точки е,лежащей на этом векторе pac
используют теорему подобия и
рассчитывают длину отрезка pae по
формуле:
204.
205.
Для определения ускорения точки Fсоставляется векторное уравнение
206.
207.
Угловые ускорения звеньев 2, 3 и 4:208.
Для определения сил инерциизвеньев при проведении силового
анализа механизма нужно знать
ускорения центров масс звеньев.
Центр масс кривошипа 1 (точка S1)
совпадает с неподвижной точкой А,
ускорение которой равно нулю.
209.
Центр масс шатуна 2 (точка S2) лежитна середине звена BC. Поэтому нужно
разделить отрезок cb на плане
ускорений на две равные части и точку
соответствующую середине отрезка cb
соединить с полюсом и обозначить S2.
210.
Центр массы шатуна 4 (точка S4)расположен, например, на расстоянии
равном 1/3 lЕF от точки Е. Разделите
отрезок ef на плане ускорений на три
равные части. Обозначьте S4 точку,
лежащую ближе к точке e. На плане
ускорений соедините точку S2 с
полюсом.
211.
Центр масс точка S5 ползунасовпадает с точкой F, поэтому ускорение
центра массы звена 5 равно ускорению
точки F.
Масса коромысла 3, например, в
соответствии с исходными данными не
задана.
212.
213.
4 Кинетостатический анализплоских рычажных механизмов
Целью кинетостатического (силового)
анализа является определение реакций
в кинематических парах механизма, а
также определение внешнего
уравновешивающего момента сил,
приложенного к ведущему звену.
214.
Сила, движущая ведущее звеномеханизма в рассматриваемом
положении и уравновешивающая
действие сил, приложенных к
механизму, называется
уравновешивающей силой Fy.
215.
Момент движущих сил, который вданном положении уравновешивает
действие всех сил в механизме, носит
название уравновешивающего момента
Му. Этот момент действует на ведущее
звено со стороны двигателя
обеспечивая вращение ведущего звена
вокруг оси.
216.
В общем случае силы движущие исилы сопротивления являются
функциями кинематических параметров
(скорости, ускорения). Эти функции для
конкретных двигателей и рабочих
машин называют механическими
характеристиками.
217.
В основу метода кинетостатикиположен принцип Д’Аламбера, согласно
которому движущееся звено можно
рассматривать как находящееся в покое,
если к действующим на него заданным
силам приложены силы инерции и
моменты инерции.
218.
Для проведения силового анализадолжны быть заданы: кинематическая
схема и размеры всех звеньев механизма,
закон движения ведущего звена, массы
звеньев, внешние силы, действующие на
звенья, а также определены силы
инерции и моменты инерции звеньев.
219.
Для определения неизвестныхреакций и уравновешивающих силы и
момента можно применить метод
планов сил. План сил можно построить
для кинематической цепи (группы
Ассура), степень подвижности которой
равна нулю.
220.
Поэтому при силовом исследованиимеханизм предварительно расчленяют
на структурные группы Ассура. При
этом действие отсоединённых при
расчленении механизма групп Ассура
заменяется силами реакций.
221.
Силовой расчет начинается дляструктурной группы, которая в процессе
создания механизма присоединена последней, и заканчивается расчетом
ведущего звена.
222.
Под реакциями в кинематическихпарах подразумеваются силы, с
которыми звенья механизма
воздействуют друг на друга.
223.
В учебных целях методикавыполнения построений планов сил
показана только для одного, например,
пятого положения механизма (см. рис.)
224.
Силовой анализ начинается сотображения точек S2 и S4 (центров
масс) на звеньях 2 и 4 плана механизма
в соответствии с исходными данными.
Точка S5 совпадает с точкой F.
225.
226.
Для определения направленияуглового ускорения звена 2 мысленно
переносится с плана ускорений вектор
тангенциальной составляющей
(вектор n2c на плане ускорений)
в точку С на плане механизма.
227.
Аналогично мысленно переносится вточку F вектор n4f на плане ускорений.
Векторы n2c и n4f на плане механизма
не рисуются.
В данном случае угловые ускорения ε2
и ε4 направлены против хода часовой
стрелки и отображаются дугообразными
стрелками на плане механизма.
228.
Центр масс кривошипа 1 находитсяна оси его вращения, поэтому сила
инерции кривошипа равна нулю (Fi1= 0).
Главный момент сил инерции
кривошипа 1 также равен нулю (Mi1 = 0),
так как угловая скорость кривошипа
величина постоянная.
229.
Инерционные нагрузки шатуна ВС(звена 2) равны:
- момент инерции звена 2
относительно центральной оси.
230.
Для шатуна EF (звена 4) инерционныенагрузки определяются аналогично.
Ползун (звено 5) не вращается и
движется поступательно, поэтому
имеет место только сила инерции
231.
Силовой анализ начинается сгруппы Ассура, включающей в себя
выходное звено (ползун).
232.
К звеньям группы прикладываютсявнешние нагрузки: сила тяжести G4,
сила тяжести G5 и сила полезного
сопротивления Р.
Вектор силы инерции звена 4,
прикладывается к центру масс в
направлении противоположном вектору
ускорения рas4.
233.
Вектор силы инерции ползунаприкладывается в точке F в
направлении противоположном
вектору ускорения этой точки рaf.
234.
Реакция R05 стойки 0 на ползун 5,(без учёта трения) направлена
вертикально вверх перпендикулярно
траектории движения ползуна 5.
Момент сил инерции Мi4 направлен
противоположно направлению углового
ускорения ε4 (показан стрелкой).
235.
Реакции во внешних кинематическихпарах группы обычно представляют в
виде нормальной и тангенциальной
составляющих. В данном случае это
составляющие соответственно
направленные параллельно и
перпендикулярно звену ЕF).
236.
237.
Отобразите плечо hG4 силы G4.Аналогично постройте плечо hi4
силы G5
238.
239.
Силовой анализ группы Асссураначинается с определения
тангенциальной составляющей R34 .
Для этого составляется уравнение
равновесия моментов сил, действующих
на звено 4 относительно точки F:
240.
Если направление вектора быловыбрано неправильно, то результат
получился со знаком минус. В этом
случае нужно перенаправить вектор R34
на противоположное направление.
241.
242.
На схеме группы Ассура осталосьдва известных по направлению, но
n
R
неизвестных
по
модулю
вектора:
и
34
R05. Для их определения составляется
векторное уравнение равновесия сил,
действующих на группу Ассура 4–5 и
строится план сил.
243.
nR34 R34 G4 Fi 4 G5 Fi 5 P R05 0.
Примите масштабный коэффициент
сил, который учитывается следующим
образом
.
244.
Построение плана сил начните изпроизвольной точки, из которой
отложите первый известный вектор R34 .
245.
Через конец последнего вектора Pпроводится вертикальная линия
параллельно направлению вектора R05
а через начало первого вектора R05
проводится линия параллельно
звену
n
EF (направление вектора R34)
и тем самым замыкается
многоугольник сил.
246.
247.
Для определения реакции R34соединяется стрелкой точка
пересечения вспомогательных
линий
с
концом вектора R34 .
248.
249.
Для определения реакции вовнутренней кинематической паре F
группы, записывается уравнение
равновесия сил, действующих на одно
из звеньев
группы,
например,
на
4
звено R G F R 0.
34
4
i4
54
250.
R34 G4 Fi 4 R54 0.251.
Для продолжения кинетостатическогоанализа нужно отобразить группу
Ассура 2–3.
252.
К звеньям группы 2-3прикладываются внешние нагрузки:
реакция R43, направленная
противоположно реакции R34 и сила
тяжести G2. Силой тяжести G3 в данном
конкретном случае можно пренебречь,
так как масса звена 3 не задана.
253.
По этой же причине инерционныенагрузки приладываются только к
второму звену. Сила инерции Fi2
направлена противоположно вектору
as2 на плане ускорений, а момент сил
инерции Mi2 противоположен угловому
ускорению ε2.
254.
Отображаются плечи сил,относительно общей точки С, а также
реакции во внешних кинематических
парах группы, представленные в виде
нормальных и тангенциальных
составляющих.
Направление указанных реакций
выбирается произвольно.
255.
256.
Определяются длины плечей hG2, hi2 иhR. Для этого необходимо измерить их
на плане группы Ассура и умножить
результаты измерений на масштабный
коэффициент длины.
257.
Для определениятангенциальной
составляющей R12 составляется
уравнение равновесия моментов сил
относительно точки С для звена 2:
M C R12 l BC G 2 hG 2 Fi 2 hi 2 M i 2 0.
258.
Затем для определения R03составляется уравнение равновесия
моментов сил относительно точки С для
звена 3:
M C R03 lCD R43 hR 0.
259.
Для построения плана силсоставляется векторное уравнение
равновесия сил, действующих на всю
группу Ассура 2–3. Длины векторов на
плане сил получаются делением
модулей векторов на масштабный
коэффициент
сил.
n
n
R12 R12 G2 Fi 2 R43 R03 R03 0
260.
Известные по величине инаправлению векторы последовательно
откладываются из произвольно
выбранной точки начиная с R12
аналогично как при построении плана
сил для группы Ассура 4–5.
261.
nn
R12 R12 G2 Fi 2 R43 R03 R03 0
262.
Через конец последнего вектора R03проводится прямая параллельно звену
3, а через начало первого вектора R12
проводится прямая параллельно звену
2.
263.
264.
Точка пересечениявспомогательных линий соединяется
стрелкой с концом вектора
.
R
03
Конец вектора R03 соединяется
стрелкой с началом вектора R12.
Полученные векторы
соответственно
n
n
обозначаются R03 и R12 .
265.
266.
nНачало вектора R12 соединяется
стрелкой с концом вектора
R12
.
Начало вектора R03 соединяется
n
.
03
стрелкой с концом вектора R
Полученные векторы
соответственно
обозначаются R12 и R03 .
267.
268.
Для определения реакции в шарниреС составляется уравнение равновесия
сил, действующих на коромысло ЕС:
R23 R43 R03 0.
269.
В этом уравнениинеизвестным
является вектор R23 .
R
Его начало, это конец вектора
,
03
а конец – это начало вектора R43 .
Этот вектор обозначается R23.
270.
271.
Для завершения кинетостатическогоанализа отображается входное звено
(кривошип АВ), к которому
прикладывается в точке В реакция R21,
направленная
противоположно
реакции
R12, сила тяжести G1 в точке А
направленная вертикально вниз и
неизвестная реакция R01 в точке А.
272.
273.
Векторное уравнение равновесиясил, действующих
на
кривошип,
имеет
R21 G1 R 01 0 .
вид:
274.
Для равновесия кривошипа к немудолжен быть приложен внешний
уравновешивающий момент сил Мур,
который определяется по формуле
M ур R21 h21
где – h21 плечо силы R21 .
275.
276.
5 УРАВНОВЕШИВАНИЕВРАЩАЮЩИХСЯ МАСС
Рост производительности машин
связан с увеличением рабочих скоростей
и ускорений, и, следовательно, ростом
сил инерции. Силы инерции вызывают
дополнительные динамические нагрузки
в кинематических парах.
277.
Поэтому при проектированиимеханизма стремятся к полному или
частичному устранению динамических
нагрузок. Эта задача делится на две
самостоятельные задачи:
• уравновешивание вращающихся масс
механизма;
• уравновешивание динамических
нагрузок на фундамент.
278.
Любое тело вращающеесяотносительно неподвижного тела
называется ротором. Даже
симметричный по конструкции ротор
может быть неуравновешен вследствие
неоднородности материала, неточности
изготовления, погрешностей монтажа.
Различают три варианта
неуравновешенности ротора.
279.
1. Статически неуравновешенныйротор - ротор, у которого главный
вектор сил инерции не равен нулю, а
главный момент сил инерции равен
нулю
280.
В этом случаеглавная
центральная ось
инерции
параллельна оси
вращения
ротора.
281.
2. Моментно неуравновешенный ротор- ротор, у которого главный вектор сил
инерции равен нулю, а главный момент
сил инерции не равен нулю
282.
В этом случаеглавная центральная
ось инерции и ось
вращения ротора
пересекаются в
центре масс.
283.
3. Динамически неуравновешенныйротор - ротор, у которого и главный
вектор, и главный момент сил инерции
не равны нулю
284.
В этом случаеглавная
центральная ось
инерции и ось
вращения ротора
пересекаются вне
центра масс или
скрещиваются.
285.
Уравновешивание роторовосуществляют установкой на него
дополнительных масс. Различают
статическое, моментное и
динамического уравновешивание
286.
Например, масса mвращается с угловой
скоростью ω вокруг оси А.
В этом случае возникает
сила инерции
вызывающая переменное
нагружение опоры А.
287.
Установим противовес тп, которыйприведет к возникновению силы
инерции
, равной по величине, но
противоположно направленной к силе
инерции , т.е.
После преобразования получаем
288.
Зададимся массой тп иопределим радиус rп .
В общем случае условие
статического
уравновешивания
289.
Произведениетr называется
дисбалансом.
Рассмотрим
статическое
уравновешивание
нескольких масс:
m1, m2 и m3.
290.
Для того, чтобы центр масссовместить с точкой А, необходимо,
чтобы выполнялось условие
291.
Задаваясь масштабнымкоэффициентом, строим векторный
многоугольник дисбалансов и получаем
дисбаланс противовеса, и его
направление.
292.
293.
Задаваясь массой, определим радиусrп или наоборот. Вместо постановки
противовеса можно убрать массу с
противоположной стороны ротора,
равную тп на расстоянии rп .
294.
На практике уравновешиваниебыстровращающихся деталей
(балансировку) производят на
специальных балансировочных
машинах. Причем, сначала выполняется
статическое уравновешивание, затем
уравновешивание моментное и только
потом динамическое.
295.
6 Уравнения и стадии движениямеханизма
Уравнениями движения называют
аналитические зависимости,
которые связывают силы,
действующие на звенья механизма, с
параметрами движения этих звеньев.
296.
Начальное звено механизмапринимается за звено приведения.
Момент инерции этого звена Jn
относительно оси вращения называется
приведенным моментом инерции.
Момент Мп пары сил, действующей на
звено приведения, называется
приведенным моментом сил.
297.
В механизмах с одной степенью свободы приняторазличать три стадии (режима) работы: разбег,
установившееся движение и выбег.
298.
Время разбега tразбега механизмахарактеризуется возрастанием скорости
начального звена от нуля до некоторого
значения, соответствующего началу
установившегося движения.
299.
Время установившегося движенияхарактеризуется периодическим
изменением скорости начального звена.
Время выбега tвыбега характеризуется
убыванием скорости начального звена
до нулевого значения.
300.
Промежуток времени tцикла, поистечении которого положения,
скорости и ускорения начального звена
принимают свои первоначальные
значения, восстанавливается запас
кинетической энергии, называется
циклом установившегося движения
механизма.
301.
Уравнение движения машины режимеустановившегося движения, используя
теорему об изменении кинетической
энергии, можно записать:
302.
где Т - кинетическая энергиямашины в конечный момент времени;
То - кинетическая энергии машины в
начальный момент времени; Ад - работа
движущих сил; Апс - работа сил
производственного сопротивления; Авс работа сил вредного сопротивления.
303.
Если на стадии разбега То = 0, то:Следовательно, на стадии разбега
при запуске механизма движущие
силы должны не только преодолеть
силы сопротивлений, но и сообщить
кинетическую энергию.
304.
Время цикла установившегося движения tц,то есть минимальный промежуток времени,
по
истечении
которого
обобщенная
координата
и
кинетическая
энергия
механизма принимают начальные значения.
305.
Изменение кинетической энергии завесь период установившегося движения
равно нулю, и тогда уравнение
принимает следующий вид:
Из уравнения видно, что чем меньше
работа сил вредного сопротивления
(трения и др.), тем эффективнее
используется энергия в машине.
306.
На стадии выбега (останова)скорости звеньев механизма убывают до
нуля, движущие силы отключают, и
поэтому Аd = 0. В конце выбега T=0, и
уравнение имеет вид:
307.
Когда вся кинетическая энергиямеханизма оказывается
израсходованной на преодоление сил
сопротивлений, механизм
останавливается. Для уменьшения
времени останова используются
тормозные устройства.
308.
7 Коэффициент полезногодействия механизмов
Одним из важнейших параметров,
оценивающих работу и качество машин
и механизмов, а также эффективность
использования ими поступающей
энергии, является коэффициент
полезного действия (КПД).
309.
Механическим КПД механизма η называют отношение работы Wп.c(мощности Pп.c) сил полезных
сопротивлений к работе WД (мощности
PД) движущих сил.
310.
О механических потерях напреодоление сил вредного
сопротивления судят по отношению
значения потерянной работы
(мощности), к работе (мощности)
движущих сил. Эту величину называют
коэффициентом потерь механизма
311.
Во всех механизмах КПД меньше единицы.Значения КПД многих механизмов определяют
экспериментально. Они приводятся также в
справочниках. КПД для ряда механизмов
можно рассчитать, зная их основные
параметры.
312.
Повысить КПД можно путем:• уменьшения потерь на трение в
кинематических парах;
• использования механизмов при
полной нагрузке;
• выбора рациональных схем
механизмов
313.
Чаще всего механические приводысостоят из совокупности отдельных
механизмов, соединенных между собой
для передачи движения
последовательно, параллельно или
смешанным способом. КПД привода
зависит от КПД каждого механизма и
характера его расположения.
314.
При последовательном соединениив машине n механизмов КПД машины
равен произведению КПД частных
механизмов, входящих в этот ряд
315.
С увеличением числа механизмовобщий КПД привода уменьшается и
всегда меньше наименьшего из КПД
механизмов, входящих в привод.
316.
При параллельном соединении n механизмовработа движущих сил выражается равенством
317.
гдекоэффициенты,
показывающие, какая часть работы всех
движущих сил подведена к первому,
второму и последующим механизмам;
следовательно,
.
Общий КПД механизмов в этом
случае определяется так:
318.
При смешанном соединении nмеханизмов общий КПД
319.
где- коэффициенты,
показывающие, какая часть работы
движущих сил от механизма М3
подведена к механизмам М4, М5, М6.
КПД механизмов на практике обычно
задаются или определяются
экспериментально.

















































































































































































































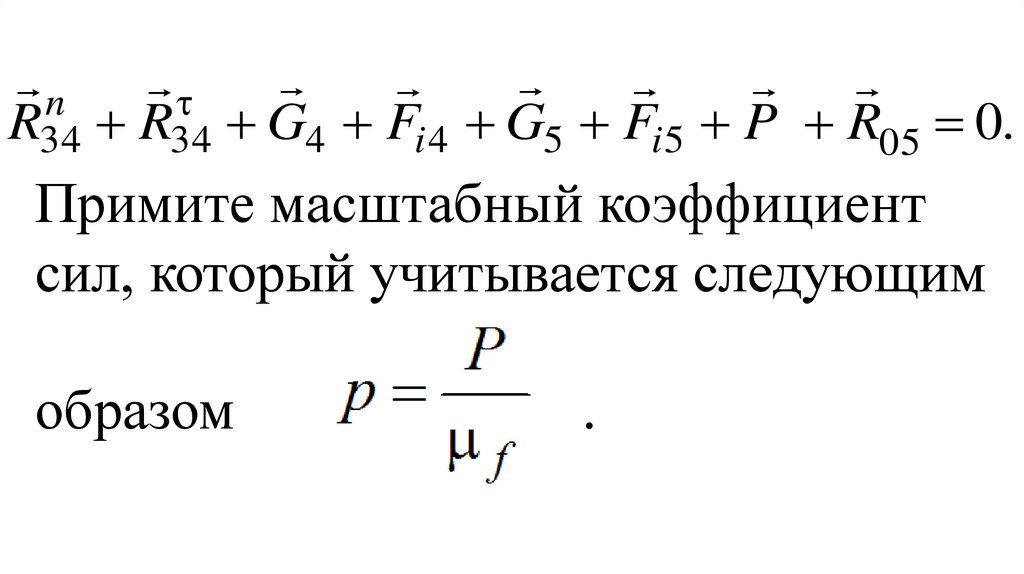
































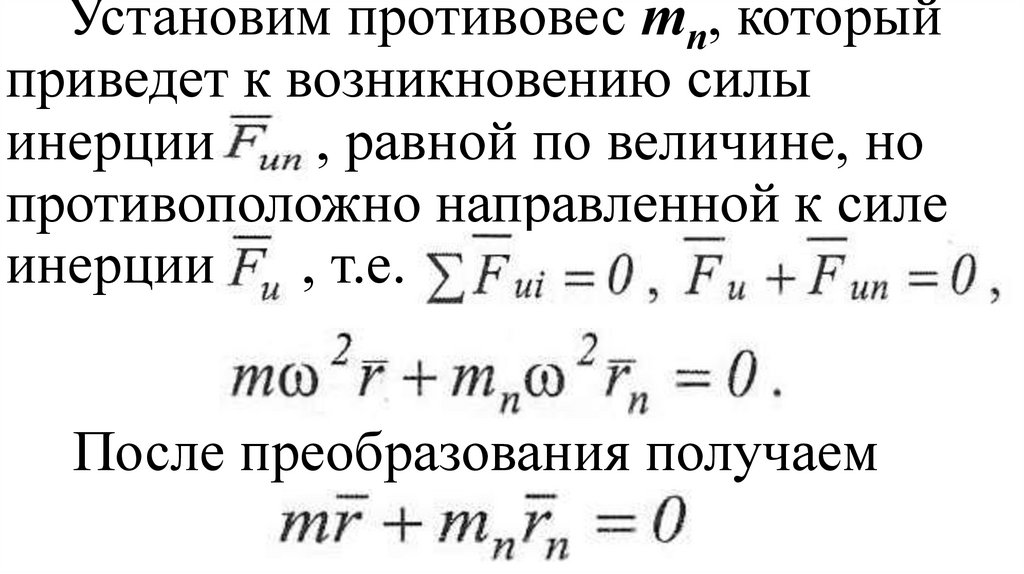




























 Механика
Механика








