Похожие презентации:
Тема №3. Занятие №5. Особенности третичной обработки радиолокационной информации
1.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙУНИВЕРСИТЕТ
Военный учебный центр
ОСНОВЫ ОБРАБОТКИ И ПЕРЕДАЧИ
ИНФОРМАЦИИ В АСУ
Тема №3 Автоматизация третичной обработки РЛИ
Занятие № 5 Особенности третичной обработки
радиолокационной информации. Группирование и
усреднение координатных точек
Руководитель занятия:
преподаватель кафедры АСУ ВКС
майор запаса Бейльман С.В.
2.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТУчебные вопросы:
1. Группирование
точек.
2. Усреднение
отождествлённых
точек.
координатных
координат
координатных
2
3.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТУчебный вопрос № 1
Группирование координатных
точек
3
4.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ4
5.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТПри выявлении возможных гипотез учитывается
правило, согласно которому, КТ полученные от
одного источника, принадлежат к различным
локационным объектам.
Для рассматриваемого примера каждой гипотезе
соответствуют две группы. В состав одной группы
следует включить две КТ от различных источников и
одну из экстраподяционных точек (ЭТ1 или ЭТ2), в
состав другой группы - оставшиеся две КТ и другую
ЭТ.
При этом получаем четыре варианта (рис. 1), т.е.
выявляем
четыре
альтернативные
гипотезы
группирования,
не
противоречащие
условию
логического правила "а".
5
6.
Варианты группирования ЭТ и КТ11
12
ЭТ1
ЭТ 2
21
22
Рис.1а
6
7.
Варианты группирования ЭТ и КТ11
12
ЭТ1
ЭТ 2
21
22
Рис.1б
7
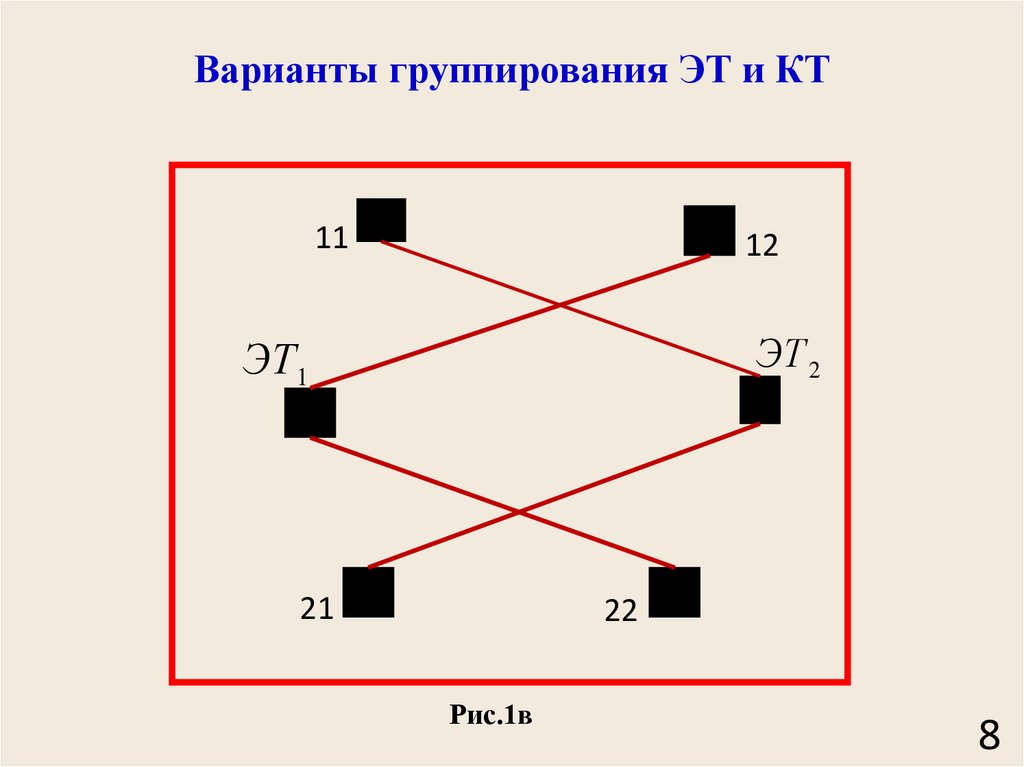
8.
Варианты группирования ЭТ и КТ11
12
ЭТ 2
ЭТ1
21
22
Рис.1в
8
9.
Варианты группирования ЭТ и КТ11
12
ЭТ 2
ЭТ1
21
22
Рис.1г
9
10.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТОбсудим методику выявления возможных
вариантов группирования для произвольного
числа КТ от нескольких источников.
Пусть (m-1) - число удаленных источников
РЛИ , а их общее число (с учетом пункта
объединения как источника ЭТ обобщенных
траекторий) - m.
Проранжируем источники, т.е. пронумеруем
их таким образом, чтобы число КТ (ЭТ) группы
А последующего номера было - не меньше, чем
предыдущего.
В таком случае справедливо неравенство:
n1 n2 n3 ..... nm
10
11.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ11
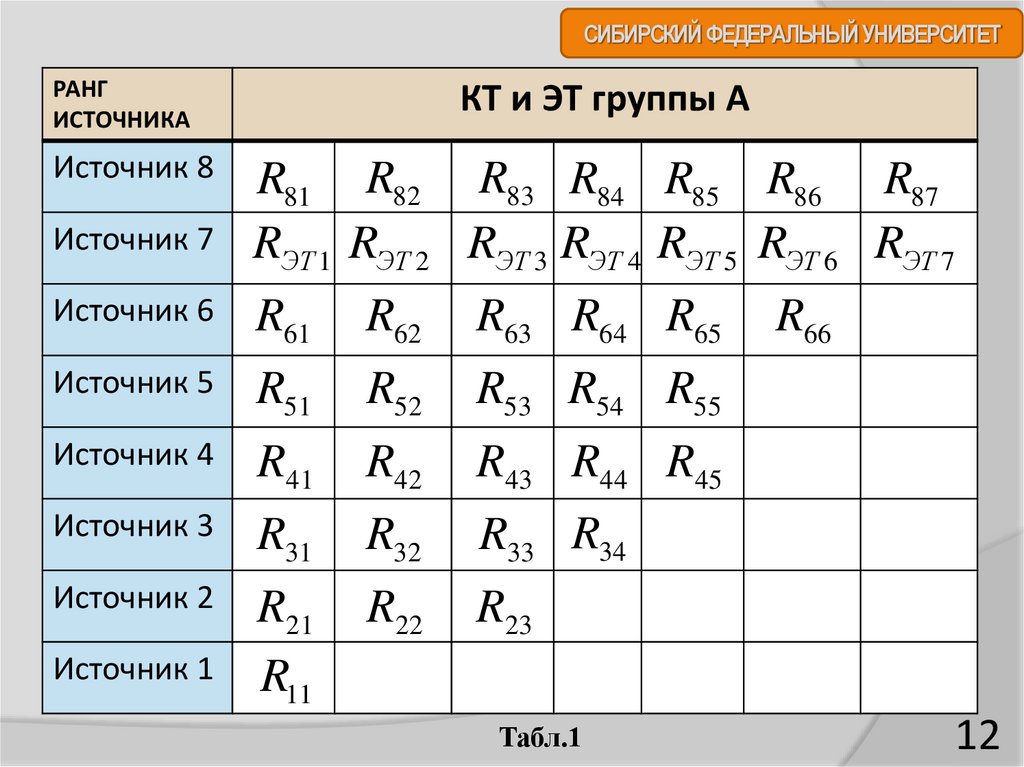
12.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРАНГ
ИСТОЧНИКА
КТ и ЭТ группы А
Источник 8
R81 R82 R83 R84 R85 R86 R87
RЭТ 1 RЭТ 2 RЭТ 3 RЭТ 4 RЭТ 5 RЭТ 6 RЭТ 7
Источник 7
Источник 6
R61
R62
R63 R64 R65
Источник 5
R51
R52
R53 R54 R55
Источник 4
R41
R42
R43 R44 R45
Источник 3
R31
R32
R33 R34
Источник 2
R21
R11
R22
R23
Источник 1
Табл.1
R66
12
13.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ13
14.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ(1)
14
15.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ15
16.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ16
17.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ17
18.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ(2)
18
19.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТТак, например, для условий задачи на рис.1 (от двух
источников по две КТ и от одного - две ЭТ) количество
гипотез группирования
а для условий таблицы количество гипотез
группирования весьма велико - примерно 1,99*1020. На
практике количество источников информации обычно не
превышает трех-четырех, а число стробированных КТ не
столь значительно, как в приведенном примере. Поэтому
количество гипотез существенно меньше. Заметим, что
рассмотренный
алгоритм
выявления
гипотез
группирования несложно реализовать программным
способом на ЭВМ.
19
20.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТГруппирование КТ с учетом
ЭТ обобщенных траекторий
20
21.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТгипотеза H 1 - R11 , R21 , RЭТ 1 - относятся к
траектории 1, а
R12 , R22 , RЭТ 2 - к траектории 2;
гипотеза H 2 -
R11 , R22 , RЭТ 2 - относятся к
траектории 1, а
R12 , R21 , RЭТ 2 - к траектории 2;
гипотеза H 3 . - R12 , R22 , RЭТ 1 относятся к траектории 1,
R11 , R21 , RЭТ 2 - к траектории 2;
гипотеза H 4
R12 , R21 , RЭТ 1 - относятся к траектории 1
R11 , R22 , RЭТ 2 - к траектории 2.
21
22.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРезультатом статистического отождествления КТ
является выбор одной из альтернативных гипотез. При
этом возможны ошибочные решения. Каждому
ошибочному решению поставим в соответствие
некоторую стоимость (штраф). Для правильных
решений стоимости считаются равными нулю. В
данной задаче нет оснований считать, что ошибочные
решения имеют различные стойкости. Поэтому в
качестве критерия оптимального выбора той или иной
гипотезы
может
быть
использован
критерий
максимального правдоподобия.
Согласно критерию максимального правдоподобия,
верной считается та гипотеза, для которой
соответствующая функция правдоподобия имеет
максимальное значение.
22
23.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТДля четырех гипотез составим четыре функции
правдоподобия, каждая из которых представляет
совместную
плотность
вероятности
координат
полученных КТ при условии их принадлежности к
соответствующим обобщенным траекториям:
X 11 , Y11 , X 21 , Y21 / X ЭТ 1 , YЭТ 1;
LH 1 W
X 12 , Y12 , X 22 , Y22 / X ЭТ 2 , YЭТ 2
X 11 , Y11 , X 22 , Y22 / X ЭТ 1 , YЭТ 1;
LH 2 W
X 12 , Y12 , X 21 , Y21 / X ЭТ 2 , YЭТ 2
23
24.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТX 12 , Y12 , X 22 , Y22 / X ЭТ 1 , YЭТ 1;
LH 3 W
X 11 , Y11 , X 21 , Y21 / X ЭТ 2 , YЭТ 2
X 12 , Y12 , X 21 , Y21 / X ЭТ 1 , YЭТ 1;
LH 4 W
X 11 , Y11 , X 22 , Y22 / X ЭТ 2 , YЭТ 2
24
25.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТLH 1 W X11,Y11 / X ЭТ 1,YЭТ 1 W X 21,Y21 / X ЭТ 1,YЭТ 1
W X12 ,Y12 / X ЭТ 2 ,YЭТ 2 W X 22 ,Y22 / X ЭТ 2 ,YЭТ 2
LH 2 W X11,Y11 / X ЭТ 1,YЭТ 1 W X 22 ,Y22 / X ЭТ 1,YЭТ 1
W X12 ,Y12 / X ЭТ 2 ,YЭТ 2 W X 21,Y21 / X ЭТ 2 ,YЭТ 2
LH 3 W X12 ,Y12 / X ЭТ 1,YЭТ 1 W X 22 ,Y22 / X ЭТ 1,YЭТ 1
W X11,Y11 / X ЭТ 2 ,YЭТ 2 W X 21,Y21 / X ЭТ 2 ,YЭТ 2
LH 4 W X12 ,Y12 / X ЭТ 1,YЭТ 1 W X 21,Y21 / X ЭТ 1,YЭТ 1
W X11,Y11 / X ЭТ 2 ,YЭТ 2 W X 22 ,Y22 / X ЭТ 2 ,YЭТ 2
(3)
25
26.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТX ij X ЭТК
X ij / к
Rij / к
Yij YЭТК
Yij / к
(4)
26
27.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВ таком случае функции правдоподобия (3) принимают вид:
LH 1 W R11/1 W R21/1 W R12/2 W R22/2
LH 2 W R11/1 W R22/1 W R12/2 W R21/2
LH 3 W R12/1 W R22/1 W R11/2 W R21/2
(5)
LH 4 W R12/1 W R21/1 W R11/2 W R22/2
27
28.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТKij / к
2
2
X2 Xij
Xk
2
X
K XY
K XY
2
Y
(6)
2
Xij
2
Xk
Y2 Yij2 Yk2
Yij2
Yk2
28
29.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТW Rij / k
1
2 Kij / k
1/2
1
2
2
2
2
exp
y X ij / k 2 K XY X ij / k Yij / k x Yij / k
2 Kij / k
C exp Qij / k
где
C
1
2 K ij / k
1/2
(7)
— постоянный множитель, нормирующий площадь
под кривой распределения единице;
1
Qij / k
y2 X ij2/ k 2 K XY X ij / k Yij / k x2 Yij2/ k
2 Kij / k
- квадратичная
форма
29
30.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТС учетом (7) функции правдоподобия (5) принимают вид:
LH 1 C exp Q11/1 exp Q21/1 exp Q12/2 exp Q22/2
LH 2 C exp Q11/1 exp Q22/1 exp Q12/2 exp Q21/2
LH 3 C exp Q12/1 exp Q22/1 exp Q11/2 exp Q21/2
(8)
LH 4 C exp Q12/1 exp Q21/1 exp Q11/2 exp Q22/2
30
31.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТОбозначим сумму квадратичных форм каждой гипотезы одним
символом:
QH 1 Q11/1 Q21/1 Q12/2 Q22/2
QH 2 Q11/1 Q22/1 Q12/2 Q21/2
(9)
QH 3 Q12/1 Q22/1 Q11/2 Q21/2
QH 4 Q12/1 Q21/1 Q11/2 Q22/2
что позволит
компактном виде:
записать
LH 1 C exp QH 1
LH 2 C exp QH 2
функции
правдоподобии
в
LH 3 C exp QH 3
LH 4 C exp QH 4
(10)
31
32.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ32
33.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТГруппирование КТ без учета
ЭТ обобщенных траекторий
Реализация оптимального группирования связана с
определенными трудностями.
Во-первых, учет ЭТ обобщенных траекторий
эквивалентен увеличению количества источников,
информации, что приводит к существенному росту числа
гипотез группирования.
Во-вторых, оптимальный выбор гипотез связан с
заданием
корреляционных
матриц
распределений
координатной информации, элементы которых известны
весьма приблизительно. В этой связи представляют
интерес практически реализуемые квазиоптимальные
алгоритмы группирования.
33
34.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТНа практике нередко используется алгоритм
группирования, выполняемый в три этапа.
На первом этапе группируются КТ без учета ЭТ
обобщенных траекторий.
На втором этапе рассчитываются усредненные
координаты
и
параметры
движения
сгруппированных КТ.
На третьем этапе выполняется привязка
усредненных координат и параметров движения к
обобщенным траекториям.
34
35.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТR11
R12
R21
R22
35
36.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТLH 1 W R1121 W R1222
LH 2 W R1122 W R1221
(12)
36
37.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТK ijkI
X
2
2
Xij
X2
0
0
2
XkI
(13)
2
Y
Y
2
2
Yij
2
YkI
X ij X ki
2
2
Y ij Y 2kI
2
37
38.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ2
2
X ijkI
YijkI
W RijkI
exp
C exp QijkI
2
2
2 X Y
2 Y
2 X
1
(14)
LH 1 C exp Q1121 exp Q1222 C exp QH 1
LH 2 C exp Q1122 exp Q1221 C exp QH 2
(15)
38
39.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТгде QH 1 Q1121 Q1222
QH 2 Q1122 Q1221
2
2
X1121
X 1222
2
X
2
2
X1122
X1221
2
X
2
2
Y1121
Y1222
Y2
2
2
Y1122
Y1221
(16)
Y2
Согласно критерию максимального правдоподобия
выбирается тот вариант группирования КТ, для которого
сумма квадратичных форм минимальна, т.е.
1, еслиQH 1 QH 2
H
0, еслиQH 1 QH 2
1
(17)
39
40.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТДальнейшее упрощение алгоритма группирования
КТ связано с допущением о равноточности намерения
координат X и Y, т.е.
Xij XkI Yij YkI
(18)
Тогда квадратичные формы (16) оказываются
пропорциональными
сумме квадратов расстояний
между отождествляемыми КТ:
QH 1
где
2
2
I1121
I1222
2
QH 2
2
2
I1122
I1221
2
(19)
40
41.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ(20)
41
42.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ42
43.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТУчебный вопрос № 2
Усреднение координат
отождествленных КТ
43
44.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТУсреднение координат отождествленных КТ
В результате точного отождествления сведения о
каждом локационном объекте представляются группой
КТ Rij . Необходимо сформировать обобщенную
координатную точку
путем статистического
Rk
усреднения координатной информации отождествленной
КТ. Известно несколько методов усреднения, основные из
которых рассмотрим на примере усреднения координаты
X.
44
45.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТМетод средневзвешенных
Согласно
методу
средневзвешенных,
усреднение
координатной информации выполняется с учетом весовых
коэффициентов,
значение
которых
определяются
точностными характеристиками источников РЛИ:
m
X
X i 1m
Xi
i 1
где
i
(22)
Xi
X - усредненное значение координаты;
X i - значение координаты X КТ от i-го источника РЛИ;
Xi - весовой коэффициент;
m- число КТ, используемых для .усреднения.
45
46.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТЗначения весовых коэффициентов Xi определяются
дисперсиями оценивания координаты соответствующими
источниками информации:
2
(23)
Xi
Xi
Если источники информации равноточные, то соотношение
(22) упрощается:
1/
m
1
X Xi
m i 1
(24)
Согласно данному выражению, средневзвешенное
усреднение, сводится к среднему арифметическому. При
этом дисперсия ошибки усредненной координаты
уменьшается в m раз.
46
47.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТМетод предпочтительного отбора по весовому коэффициенту
В раде случаев в интересах упрощения алгоритма
третичной обработки РЛИ отказываются от метода
средневзвешенных
и
пользуются
методом
предпочтительного отбора по весовому коэффициенту.
Согласно данному методу из отождествленной группы
выбирают одну из КТ, исключая из анализа остальные.
Отобранная (опорная) КТ представляет в дальнейшем всю
группу отождествленных КТ. Метод предпочтительного
отбора по весовому коэффициенту дает менее точный
результат,
чем
метод
средневзвешенных,
однако
оправдывается в том случае, когда выбираемый источник
информации (головной) имеет существенно более высокие
точностные характеристики, чем остальные.
47
48.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТМетод предпочтительного
отбора по весовому
коэффициенту является частным случаем метода
средневзвешенных. Действительно, пусть дисперсия
2
оценивания координаты головным источником XO
2
намного меньше дисперсий Xi остальных источников.
Тогда справедливо неравенство:
XO Xi
согласно которому выражение (22) принимает вид:
m
X
X
i 1
m
Xi
i 1
i
XO X O
XO
XO
(25)
Xi
48
49.
Метод предпочтительного отбора по временипоступления информации
Согласно методу предпочтительного отбора по времени
поступления информации считается, что наименее
устаревшие данные содержат самые достоверные сведения о
локационном объекте. Поэтому координатная информация
(например, координата X) обобщенной КТ определяется по
правилу:
X X iЭ при tiЭ мин (26)
Метод
предпочтительного
отбора
по
времени
поступления информации целесообразно использовать при
обработке КТ маневрирующей цели, так как методы
усреднения,
учитывающие
устаревшие
данные,
оказываются менее точными. Среднеквадратическая
ошибка усредненной координаты при использовании
рассматриваемого метода определяется точностными
характеристиками одного источника РЛИ.
49
50.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТПривязка усредненной КТ к обобщенной траектории
Привязка усредненных координат к обобщенным
траекториям для рассматриваемого примера (от двух
источников по две КТ ) сводится к выбору одной ив двух
гипотез J1 , J 2 . Гипотезе J1 соответствует решение о
принадлежности условно первой группы КТ, имеющих
усредненные координаты X1 , Y1 к ЭТ1 (представляющей
первую обобщенную траекторию), а гипотезе J 2 - решение
о принадлежности условно второй группы КТ с
усредненными координатами X 2 , Y2 к ЭТ1.
50
51.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТРешающее правило выбора гипотез, использующее
степень взаимного отклонения усредненных координат и
ЭТ обобщенных траекторий, аналогично полученному для
выбора гипотез H 1 и H 2 т.е.
(27)
X X X X Y Y Y Y
Q
2
Где
1
2
1
2
2
2
1
1
X2
J1
2
2
Y2
X X X X
Y Y Y Y
Q
2
1
J2
2
2
2
2
1
X2
2
1
2
2
2
1
Y2
X2 , Y2 - сумма дисперсий усредненной КТ и ЭТ по
координате X и У соответственно.
51
52.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТВ первом приближении можно считать, что в результате
усреднения
координаты
ее
дисперсия
становится
соизмеримой с дисперсией ЭТ обобщенной траектории. С
учетом данного допущения решающее правило (27)
принимает вид:
(28)
52
53.
Вопросы на самоподготовку:1.
2.
3.
4.
5.
6.
7.
8.
Приведите пример возможных вариантов группирования КТ,
поступающих от трех источников информации, для которых
стробируются по две КТ.
Поясните методику группирования произвольного числа КТ.
От каких параметров зависит число вариантов группирования КТ?
Поясните физический смысл операций статистического выбора
гипотез группирования.
Каковы преимущества метода группирования КТ без учета ЭТ
обобщенных траекторий?
С какой целью выполняется задача усреднения координат отождествленных КТ?
Поясните методы усреднения координат и дайте сравнительную характеристику данных методов.
Поясните физический смысл операции привязки усредненной КТ к
обобщенной траектории.
53
54.
Литература1
Виноградов А.П. Основы обработки радиолокационной
информации. ч.3. Третичная обработка радиолокационной
информации. Военный университет ПВО г. СанктПетербург 2002 г.
2
А.Я. Матов, П.Я. Сависько, Б.М. Герасимов. Основы
обработки и передачи информации в АСУ РТВ ПВО. –
Киев: КВИРТУ ПВО, 1985.
54
55.
СИБИРСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТСПАСИБО
ЗА ВНИМАНИЕ
55





















































 Информатика
Информатика Военное дело
Военное дело








