Похожие презентации:
Обратные тригонометрические функции. Тема 9
1.
МатематикаПреподаватели:
Мовсисян Геворг Суренович,
Попова Ольга Николаевна
2.
Тема 9.Обратные
тригонометрические
функции
3.
План лекции1.Арксинус.
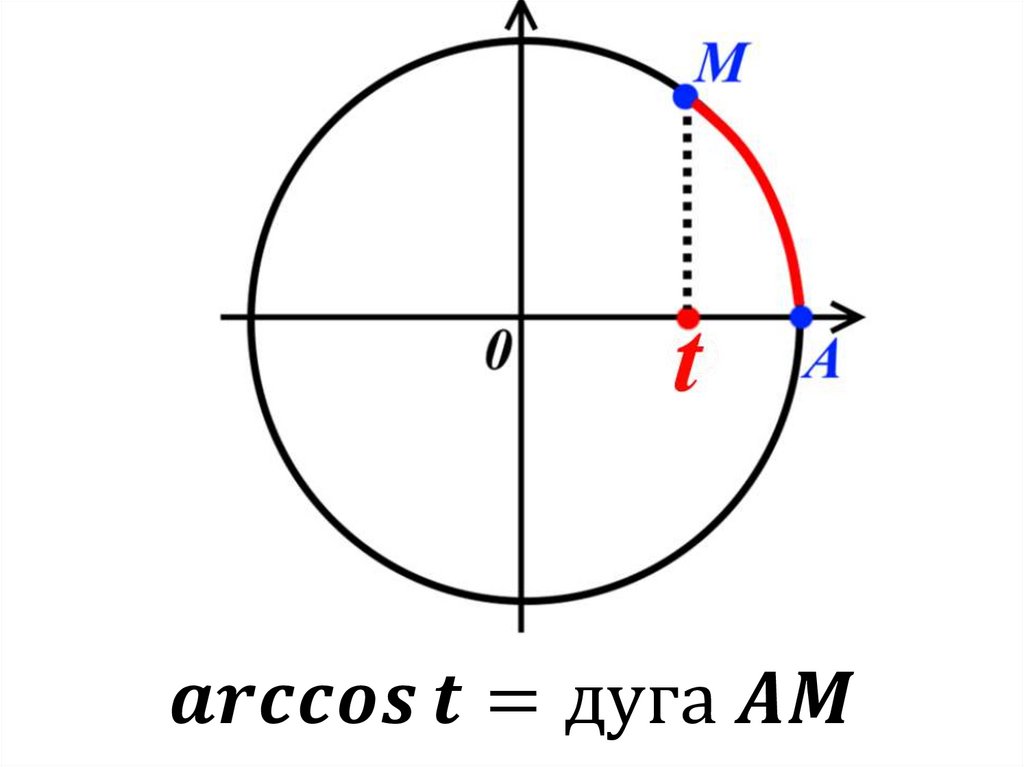
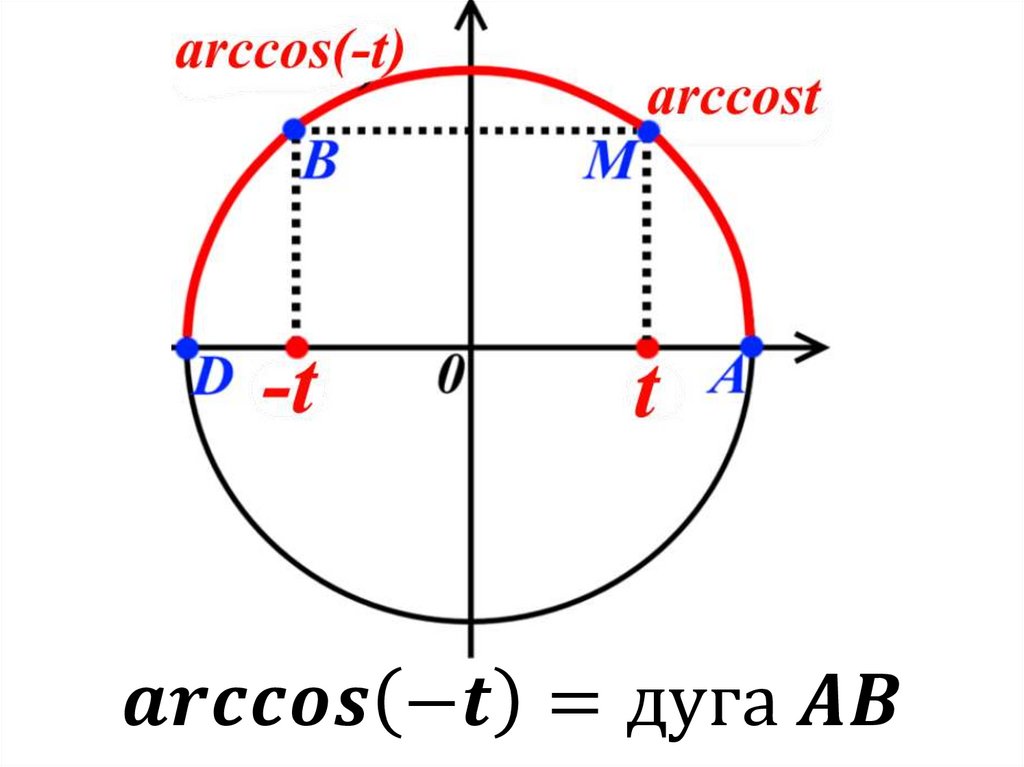
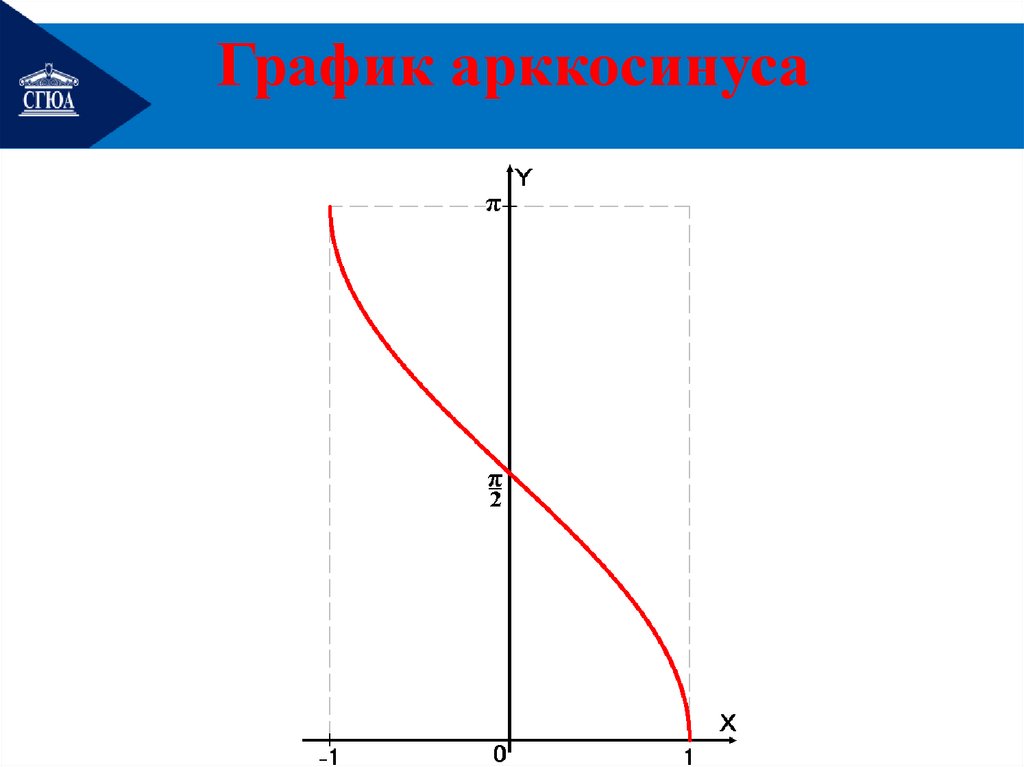
2.Арккосинус.
3.Связь арксинуса и
арккосинуса.
4.
ВведениеНазвание обратной
тригонометрической функции
образуется от названия
соответствующей ей
тригонометрической функции
добавлением приставки «арк-»
(от лат. arcus — дуга).
5.
Это связано с тем, чтогеометрически значение
обратной тригонометрической
функции можно связать
с длиной дуги единичной
окружности (или углом,
стягивающим эту дугу),
соответствующей тому или
иному отрезку.
6.
Манера обозначать такимобразом обратные
тригонометрических функции
появилась у австрийского
математика Карла Шерфера
(1716—1783г.) и закрепилась
благодаря Жозефу
Лагранжу(1736—1813г).
7.
Впервые специальный символдля обратной
тригонометрической функции
использовал Даниил
Бернулли в 1729 году.
8.
Мы знаем, каким образом длязаданного угла α
определяются значения его
тригонометрических функций
(синуса, косинуса, тангенса и
котангенса).
9.
Очень важной являетсяобратная задача: по известному
значению тригонометрической
функции угла α определить сам
угол α. При решении этой
задачи и возникают обратные
тригонометрические функции
(или аркфункции).
10.
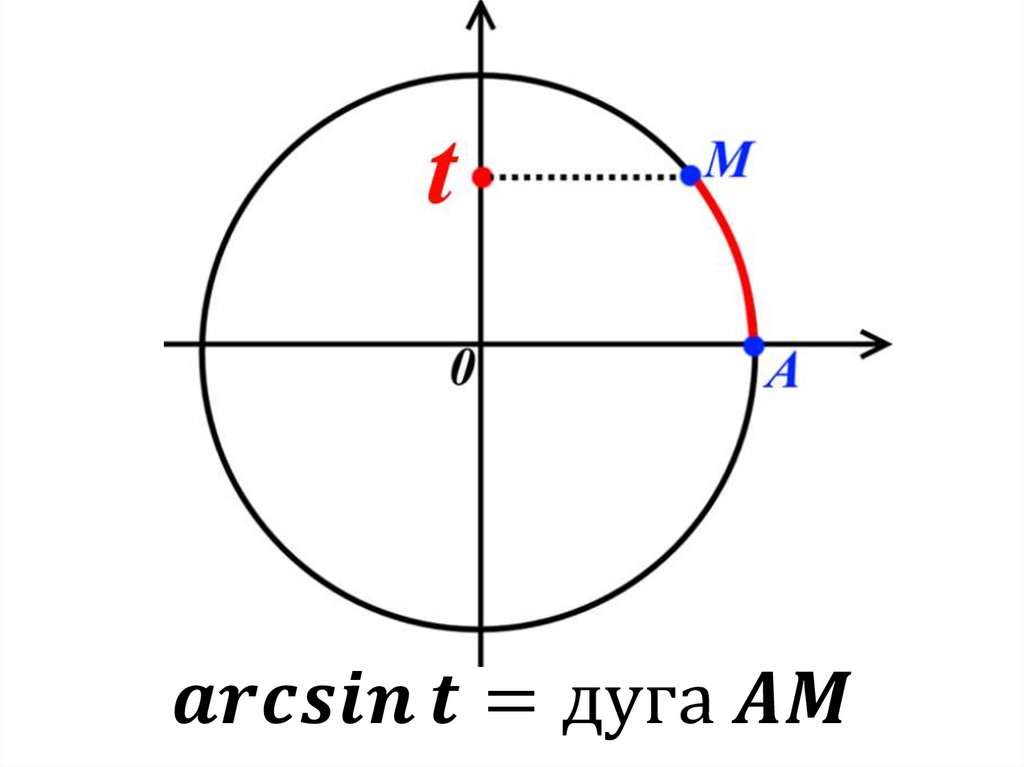
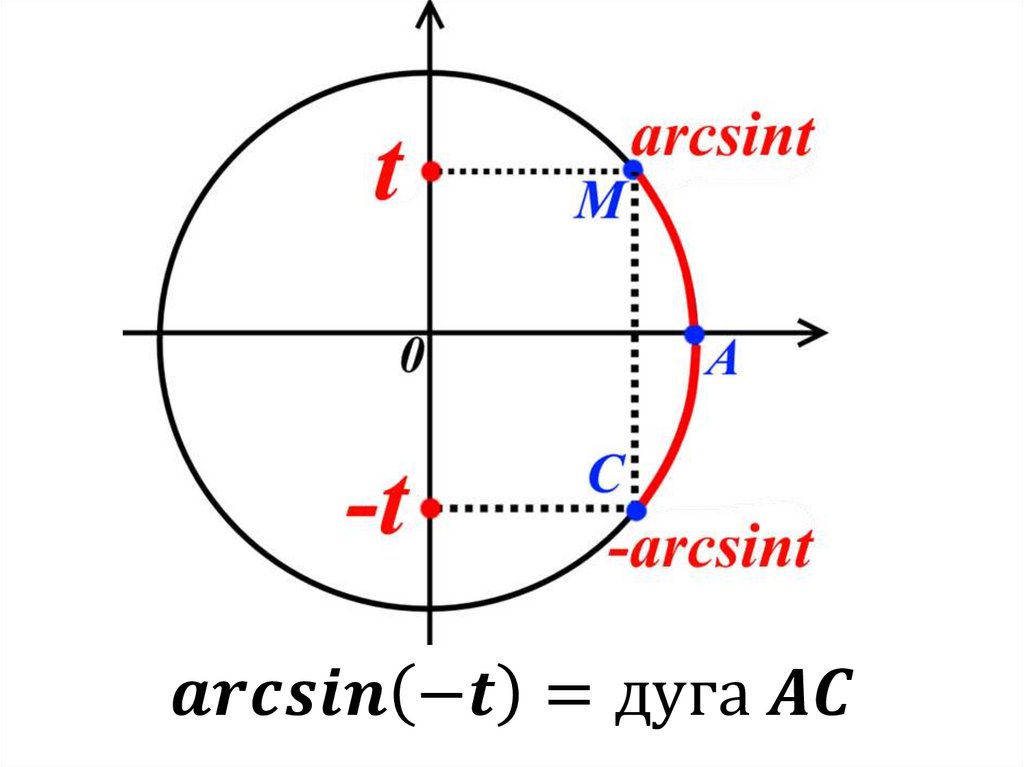
1. АрксинусОпр. Арксинусом числа

























 Математика
Математика








