Обратные тригонометрические функции

1.

Обратные
тригонометрические
функции

2.

Arcsin х
Арксинусом числа m называется
такой угол x, для которого sinx=m, π/2≤X≤π/2,|m|≤1
Функция y = sinx непрерывна и ограничена
на всей своей числовой прямой. Функция y
= arcsinx является строго возрастающей.
График обратной функции симметричен с
графиком основной функции относительно
биссектрисы I - III координатных углов.

3.

Свойства функции y = arcsin x
1)Область определения: отрезок [-1; 1];
2)Область изменения: отрезок[-π/2,π/2];
3)Функция y = arcsin x нечетная:
arcsin (-x) = - arcsin x;
4)Функция y = arcsin x монотонно
возрастающая;
5)График пересекает оси Ох, Оу в
начале координат.

4.

Arccos х
Арккосинусом числа m называется такой угол x,
для которого:
cos x = m
0≤x≤π
|m|≤1

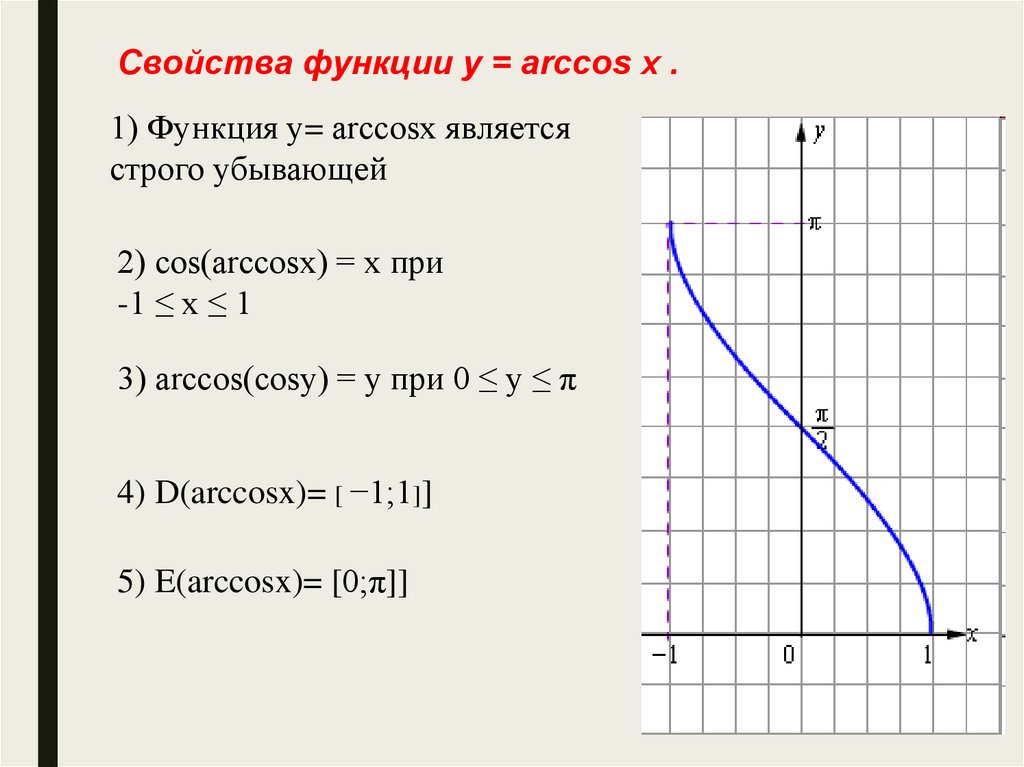
5.

Свойства функции y = arccos x .
1) Функция y= arccosx является
строго убывающей
2) cos(arccosx) = x при
-1 ≤ x ≤ 1
3) arccos(cosy) = y при 0 ≤ y ≤ π
4) D(arccosx)= [ −1;1]]
5) E(arccosx)= [0;π]]

6.

Arctgх
Арктангенсом числа m
называется такой угол x,
для которого tgx=m,
-π/2<X<π/2.
График функции y=arctgx
Получается из графика
Функции y=tgx, симметрией
Относительно прямой y=x.

7.

y=arctgх
1) Область определения: R
2) Область значения: отрезок
[-π/2,π/2];
3) Функция y = arctg x нечетная: arctg (-x) = - arctg x;
4) Функция y = arctg x монотонно возрастающая;
5) График пересекает оси Ох, Оу в начале координат.
y
2
2
yx

8.

Arcctgх
Арккотангенсом числа m
называется такой угол x, для
которого ctgx=a, 0<x<π
2

9.

Arcctgх
1) Функция y=arcctgx непрерывна и ограничена
на всей своей числовой прямой.
2) Функция y=arcctgx является строго
убывающей.
3) ctg(arcctgx)=x при xєR
4) arcctg(ctgy)=y при 0 < y < π
5) D(arcctgx)=(-∞;∞)
6) E(arcctgx)=(0; π)

10.

Преобразование выражений
Вычислить :
3tg arcsin 0,5 ;
1) 24
2) 4
2 cos arcctg1 ;
3
7 ctg
arcsin 4
.
Решение :
1
1) 24 3tg
24 3
24.
6
3
3) 12
2) 4
2 cos
4
2
2
4.
2
4
3
9
7
3) sin - , cos 1 sin 2 1
,
4
16
4
ctg
12
7
,
3
3
7ctg
arcsin
12
4
12
7 (
7
) 28.
3
3
7ctg
arcsin
4

11.

Преобразование выражений
1. Вычислить без калькулято ра
1
1
4arctg arctg
5
239
Решение :
1
1
1
1
arctg , arctg
, ттогд tg , tg
5
239
5
239
Надо вычислить В 4
Возьмем ттанген от обеих частей этого равенства :
tg 4 tg
tgB tg (4 )
1 tg 4 tg
1
5
2
2tg
5 5 , tg 4
12 120
tg 2
25
1 tg 2 1 1
12
119
1
25
144
120
1
239 120 119
tgB 119 239
1. Так как tgB 1, т B .
120 1
119 239 120
4
1
119 239
2

12.

Уравнения, содержащие
обратные тригонометрические функции
1.Решить уравнение arccos(2x 1)
3
.
4
3
0; , тт по определению арккосинус а
4
числа данное уравнение равносильно уравнению
Так как
3
2
2 2
, откуда 2x 1 ,x
.
4
2
4
2
2.Решить уравнение 2(arcsinx) 5 arcsin x 2 0.
2x 1 cos
Пусть arcsinx t, причем t - ; , тогда
2 2
2t 2 5t 2 0.
1
, но 2 - ; ,
2
2 2
1
1
arcsinx , x sin .
2
2
t 1 2, t 2

13.

Задания различного уровня сложности
Решить уравнение
2arcsin2x arccos7x.
Решение : найдем ОДЗ уравнения :
1
1
x
- 1 2x 1
2
2
или
- 1 7x 1
1 x 1
7
7
1
1
то есть - x .
7
7
На этом промежутке уравнение равносильно следующему :
cos(2arcsi n2x) cos(arccos 7x)
Так как cos(farcco s7x) 7x,
cos(2arcsi n2x) 1 - 2sin 2 (arcsin2x) 1 - 2(2x) 2 1 8 x 2
1
1 8 x 2 7 x или 8x 2 7 x 1 0, x 1, x .
8
1
С учетом ОДЗ получаем окончательно x .
8

14.

Задания различного уровня сложности
Решить задачу :
Боковая грань правильной четырехуго льной пирамиды
образует с плоскостью основания угол, равный 60 0.
Найдите угол между боковыми гранями.
Решение :
Воспользуе мся соотношением между данным и искомым
2
2
3
6
sin . Получим, что cos
.
2
2
2
2
2
4
6
1
Найдем cos 2cos 2 - 1 2 - 1 - .
2
16
4
1
Получим, что - arccos .
4
углами. cos

15.

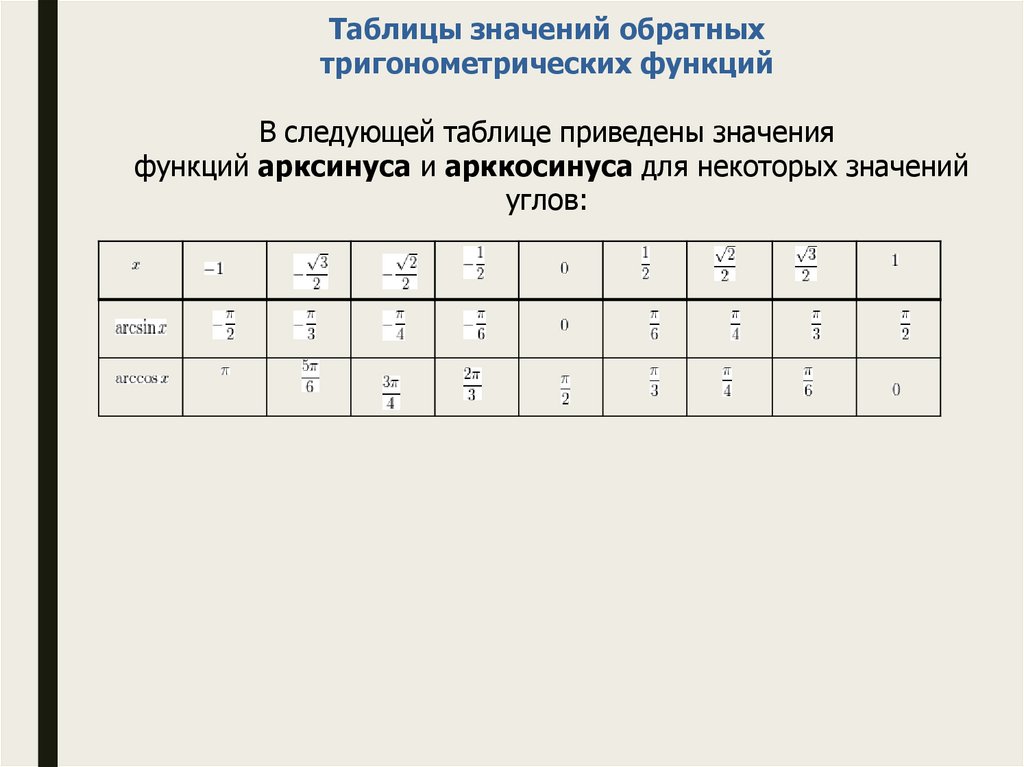
Таблицы значений обратных
тригонометрических функций
В следующей таблице приведены значения
функций арксинуса и арккосинуса для некоторых значений
углов:

16.

В следующей таблице приведены значения функций
арктангенса и арккотангенса
для некоторых значений углов: