Пифагор и его теорема

1.

«ПИФАГОР И ЕГО ТЕОРЕМА»
Проектная работа Шайхуловой Алины и Сватовой Дарины

2.

Геометрия владеет двумя сокровищами: одно из них – это
теорема Пифагора, а другое деление отрезка в среднем и
крайнем отношении. Первое можно сравнить с мерой
золота, второе же больше напоминает драгоценный
камень»
Иоганн Кеплер

3.

Цель работы
Изучение истории появления и развития теоремы
Пифагора.
Изучение исторических сведений по использованию
теоремы Пифагора.
Рассмотрение различных видов доказательств теоремы
Пифагора.
Изучить практическое применение теоремы Пифагора
Задачи:
Изучить историю появления и развития теоремы
Пифагора;
Собрать материал по использованию теоремы Пифагора
в Древние века;
Познакомиться с различными способами доказательства
теоремы Пифагора;
Узнать практическое применение теоремы Пифагора;
Исследовать пифагоровы тройки.

4.

БИОГРАФИЯ
ПИФАГОРА

5.

Биография Пифагора

6.

ШКОЛА ПИФАГОРА

7.

Школа Пифагора

8.

ИСТОРИЯ ТЕОРЕМЫ
ПИФАГОРА

9.

Гео́рг Ка́нтор — немецкий математик,
ученик Вейерштрасса. Наиболее известен
как создатель теории множеств.
Основатель и первый
президент Германского математического
общества, инициатор
создания Международного конгресса
математиков.

10.

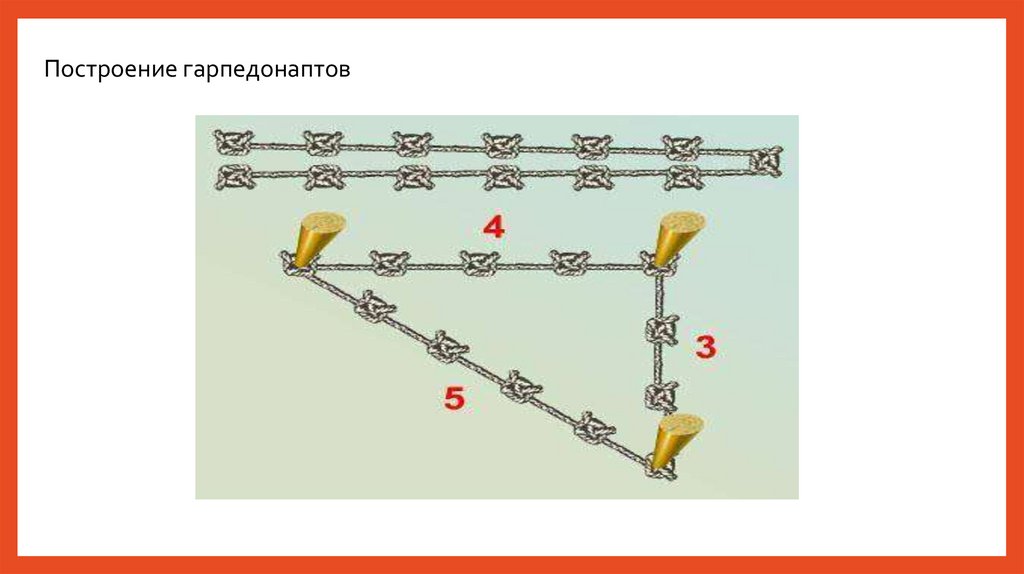
Построение гарпедонаптов

11.

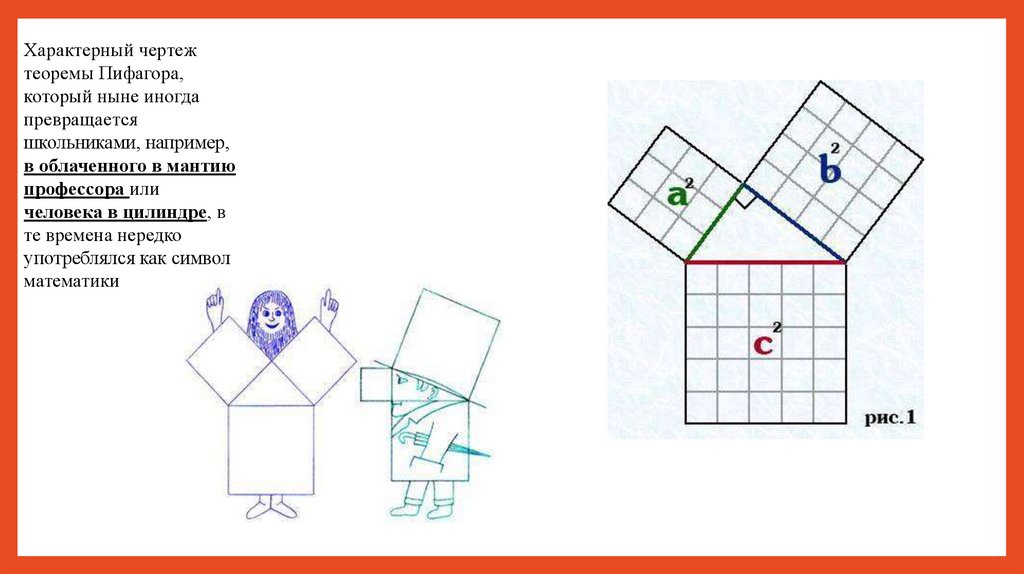
Характерный чертеж
теоремы Пифагора,
который ныне иногда
превращается
школьниками, например,
в облаченного в мантию
профессора или
человека в цилиндре, в
те времена нередко
употреблялся как символ
математики

12.

Евкли́д- древнегреческий математик,
автор первого из дошедших до нас
теоретических трактатов по
математике.

13.

Витрувий — римский архитектор и
инженер, живший в I веке до н. э.
Известен как автор формулы о
триединой сущности строительного
искусства «прочность, польза,
красота» и идеи «витрувианского
человека» — схемы пропорций
совершенного тела.
Плута́рх — древнегреческий писатель
и философ, общественный
деятель римской эпохи. Наиболее
известен как автор
труда «Сравнительные
жизнеописания», в котором
воссоздавал образы выдающихся
политических деятелей Греции и Рима.

14.

Адельбе́рт фон Шами́ссо —
немецкий писатель, поэт и естествоиспытатель (ботан
ик и зоолог). Систематик высших растений,
коллектор, флорист.
Пребудет вечной истина, как скоро
Её познает каждый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За свет луча, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, её почуя, вслед.
Они не в силах свету помешать,
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.

15.

РАЗЛИЧНЫЕ СПОСОБЫ
ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ
ПИФАГОРА.

16.

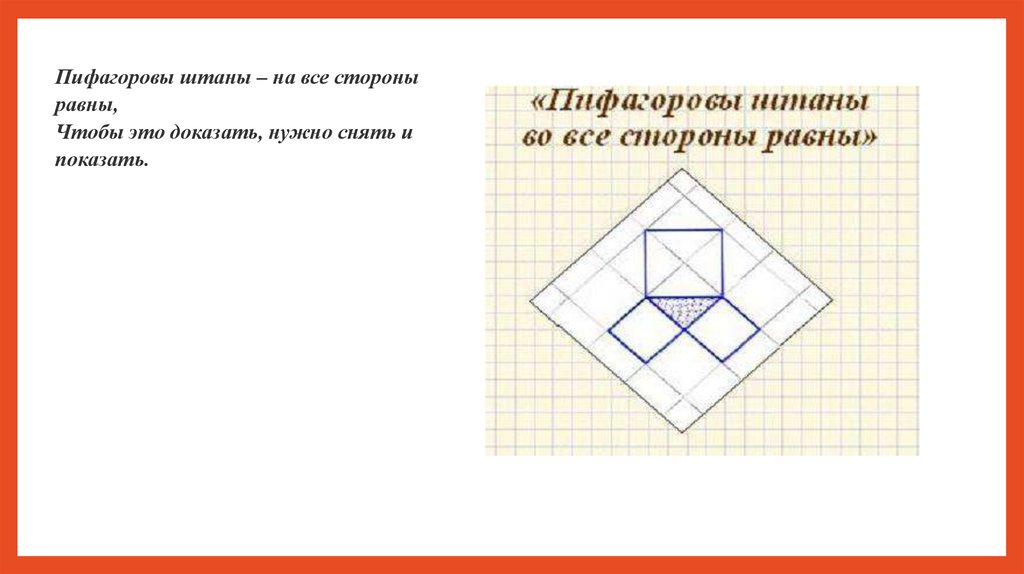
Пифагоровы штаны – на все стороны
равны,
Чтобы это доказать, нужно снять и
показать.

17.

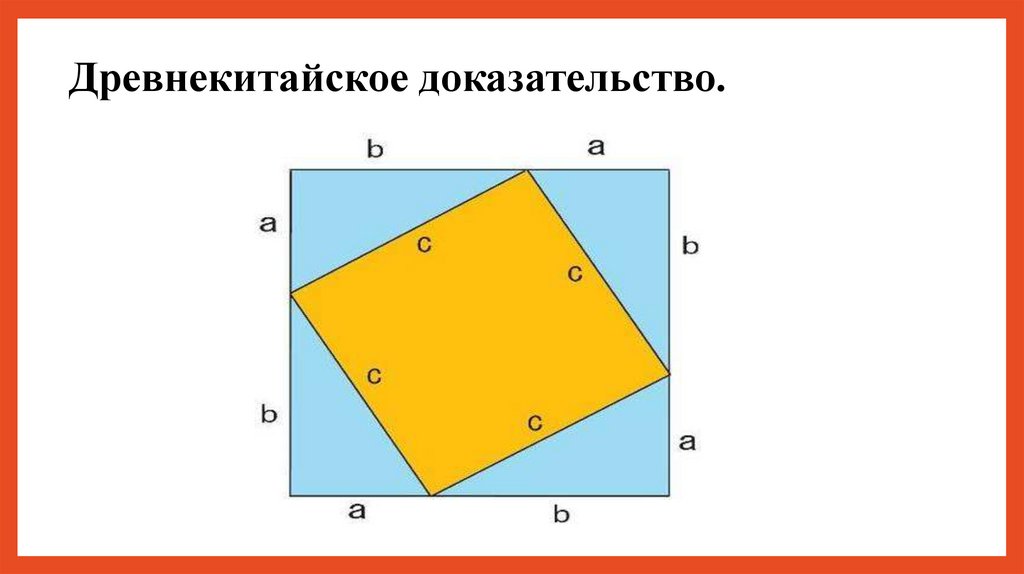
Древнекитайское доказательство.

18.

19.

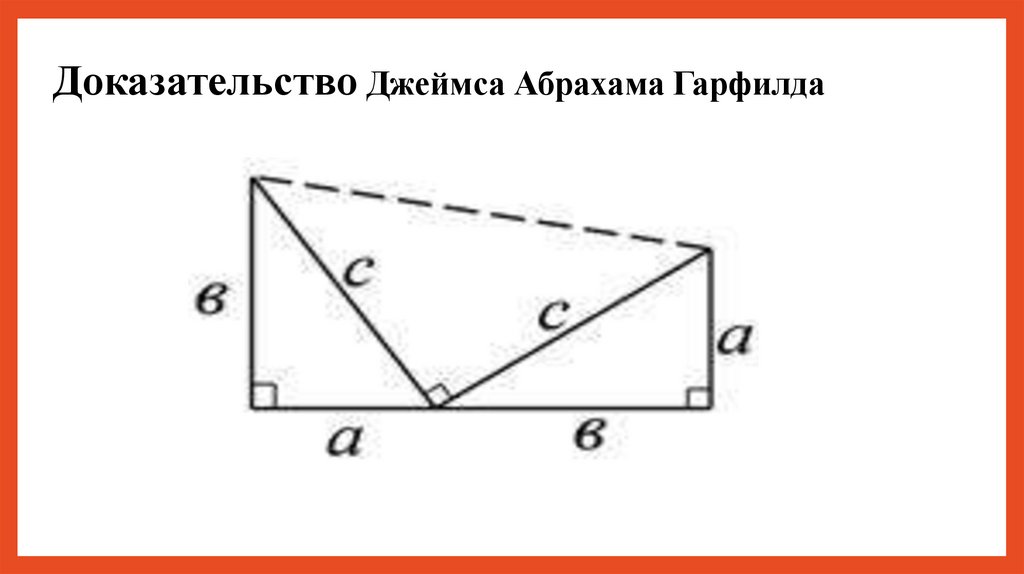
Доказательство Джеймса Абрахама Гарфилда

20.

Приравнивая эти выражения, получим
Раскрывая скобки и сокращая, получим

21.

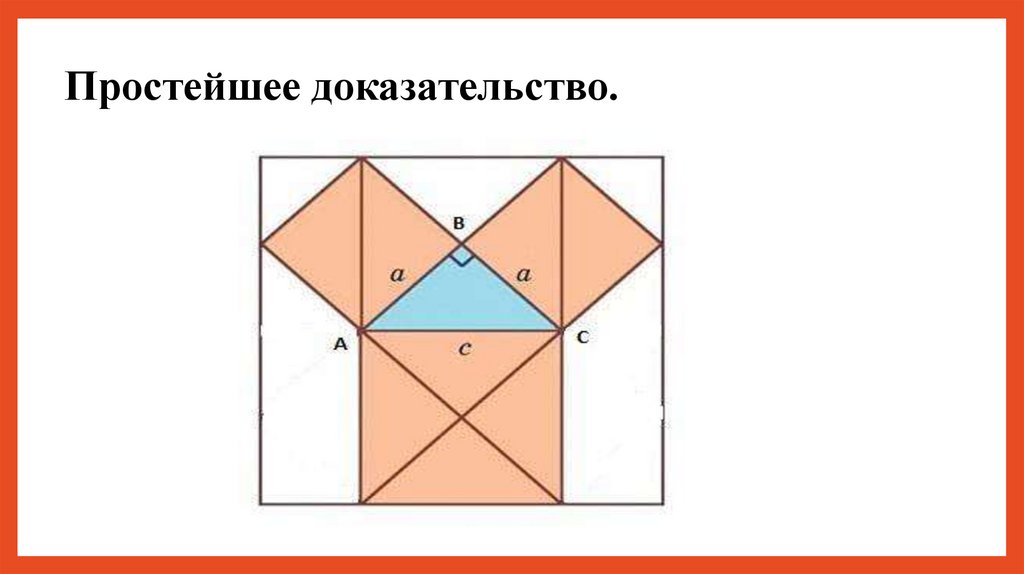
Простейшее доказательство.

22.

Доказательство Бхаскары.

23.

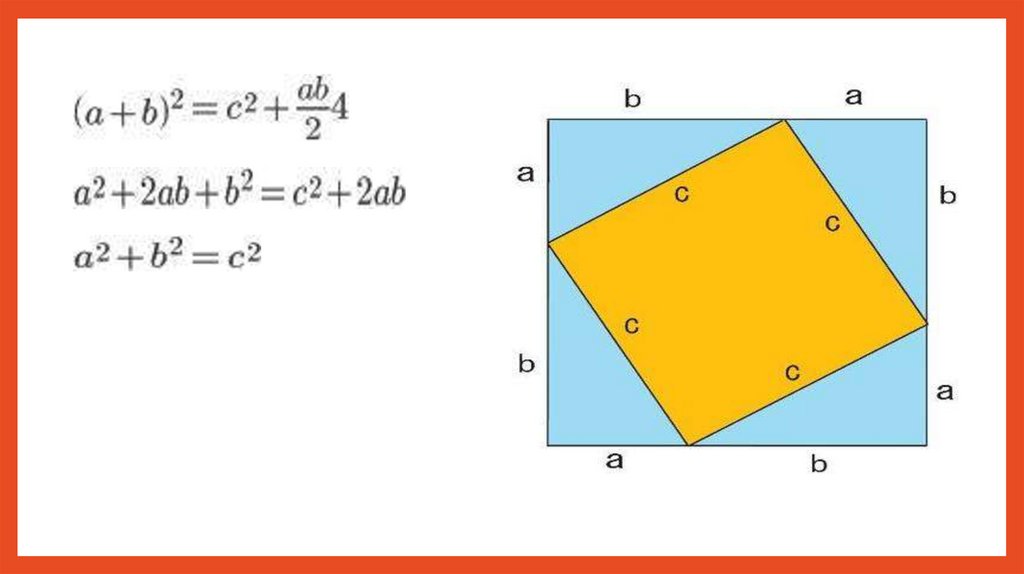
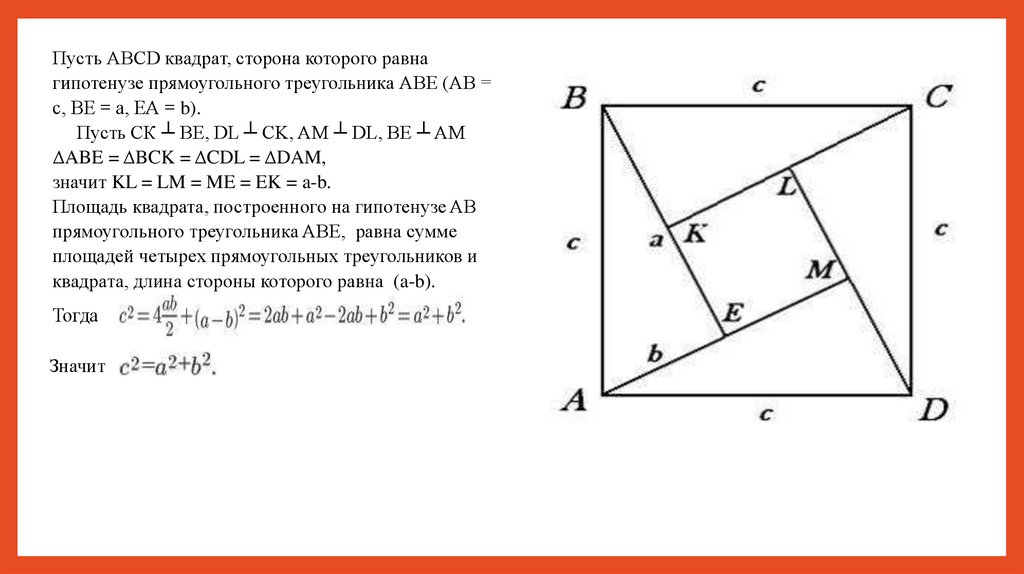
Пусть АВСD квадрат, сторона которого равна
гипотенузе прямоугольного треугольника АВЕ (АВ =
с, ВЕ = а, ЕА = b).
Пусть СК ┴ BE, DL ┴ CK, AM ┴ DL, BE ┴ AM
ΔABE = ΔBCK = ΔCDL = ΔDAM,
значит KL = LM = ME = EK = a-b.
Площадь квадрата, построенного на гипотенузе AB
прямоугольного треугольника ABE, равна сумме
площадей четырех прямоугольных треугольников и
квадрата, длина стороны которого равна (a-b).
Тогда
Значит

24.

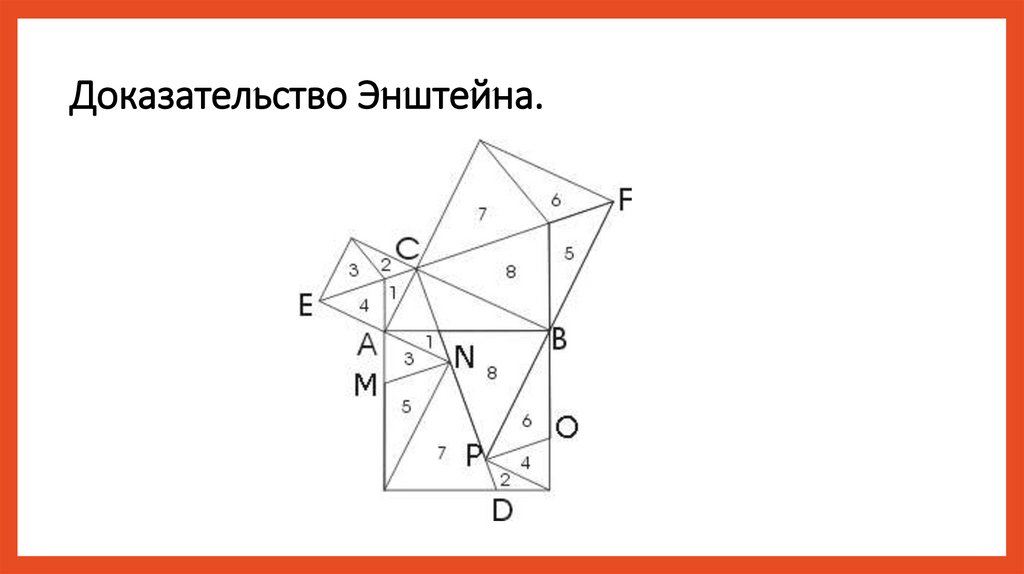
Доказательство Энштейна.

25.

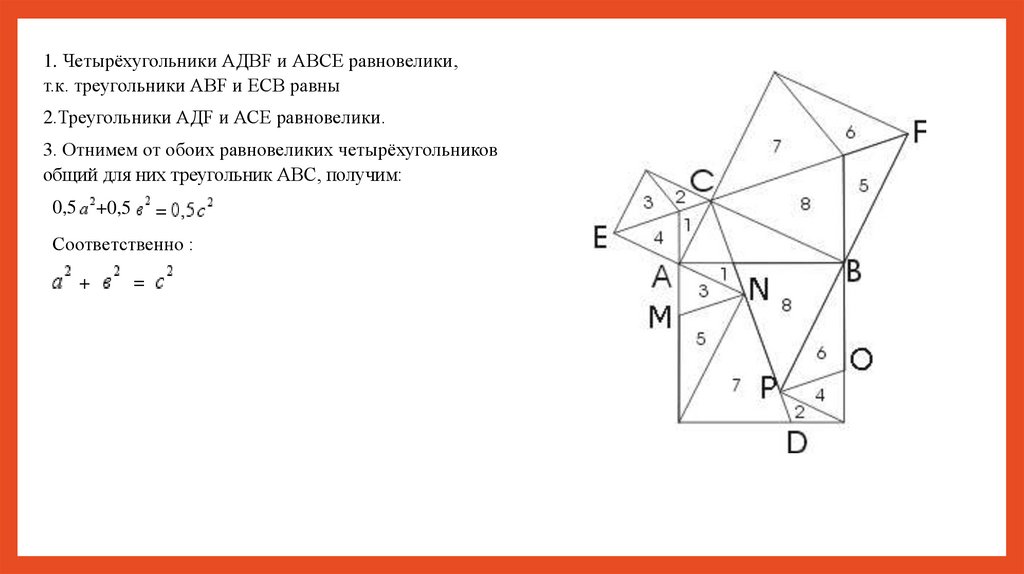
1. Четырёхугольники АДВF и АВСЕ равновелики,
т.к. треугольники АВF и ЕСВ равны
2.Треугольники АДF и АСЕ равновелики.
3. Отнимем от обоих равновеликих четырёхугольников
общий для них треугольник АВС, получим:
0,5
+0,5
=
Соответственно :
+
=

26.

Доказательство Мёльманна.
Площадь данного треугольника с одной
стороны равна 0,5ab,
с другой 0,5pr, где
p – полупериметр треугольника,
r – радиус вписанной в него окружности
(r=0,5(a+b-c)).
Имеем: 0,5ab=0,5pr=0,5(a+b+c)·0,5(a+b-c)
0,5ab=0,5(a+b+c)·0,5(a+b-c)
аb=0,5(а2 + ab – ac + ab + b2 – bc + ca + cb - с2)
аb=0,5(а2 + b2- с2 +2ab)/·2
2аb=а2 + b2- с2 +2ab
а2 + b2- с2 =0
3. Отсюда следует, что с2= а2+b2

27.

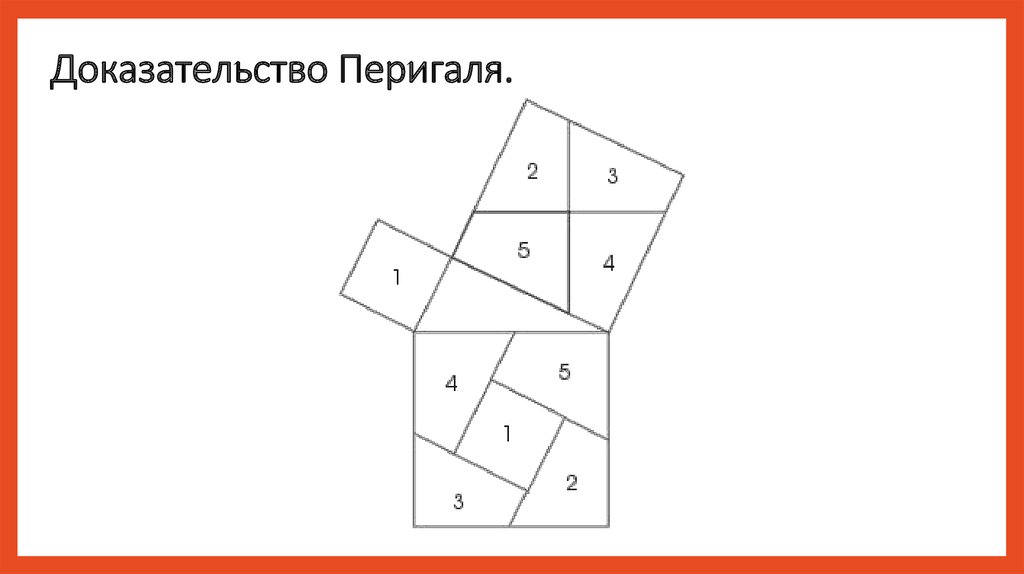
Доказательство Перигаля.

28.

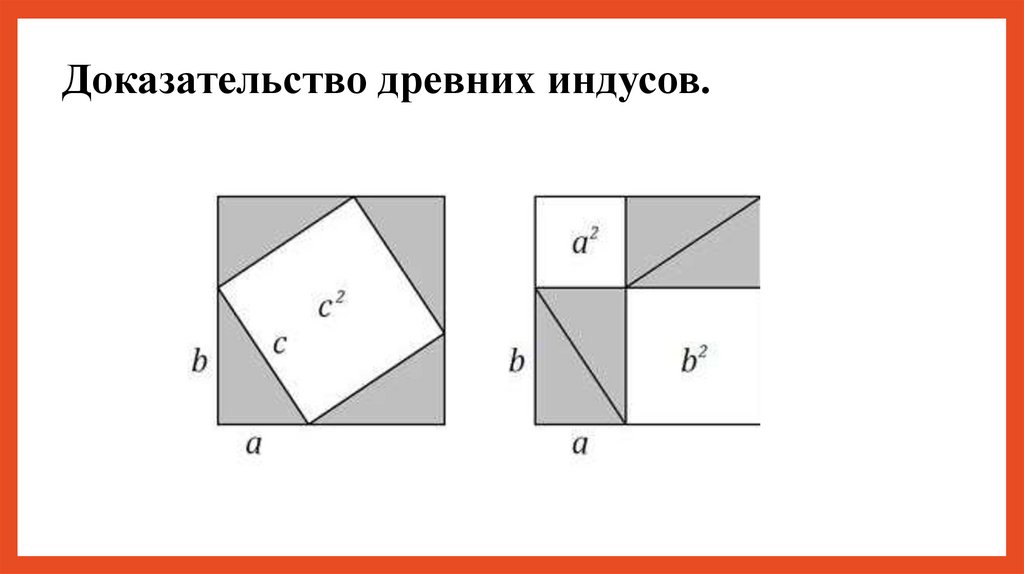
Доказательство древних индусов.

29.

ЗАНИМАТЕЛЬНЫЕ ЗАДАЧИ
ПО ТЕМЕ «ТЕОРЕМА
ПИФАГОРА».

30.

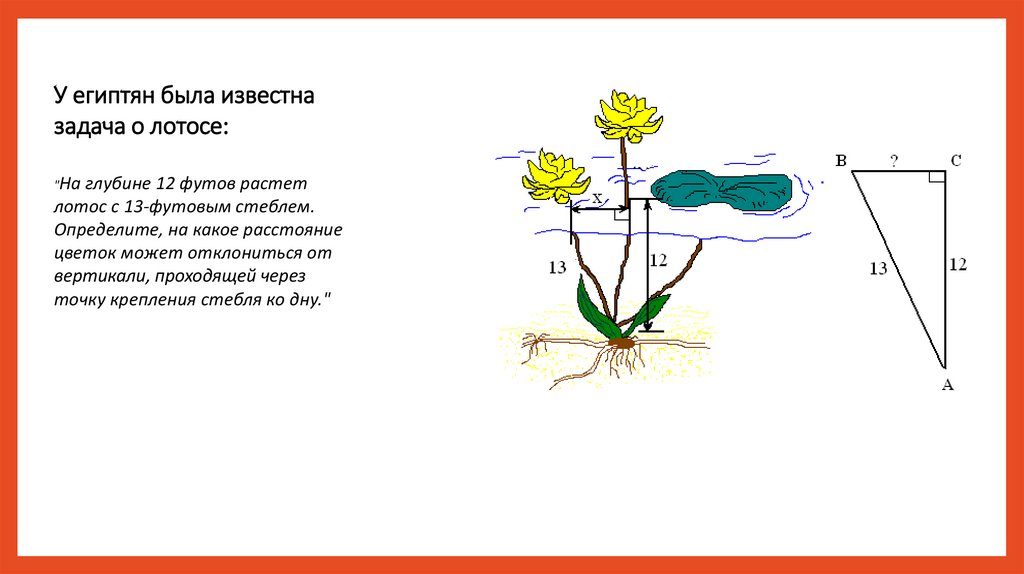
У египтян была известна
задача о лотосе:
"На
глубине 12 футов растет
лотос с 13-футовым стеблем.
Определите, на какое расстояние
цветок может отклониться от
вертикали, проходящей через
точку крепления стебля ко дну."

31.

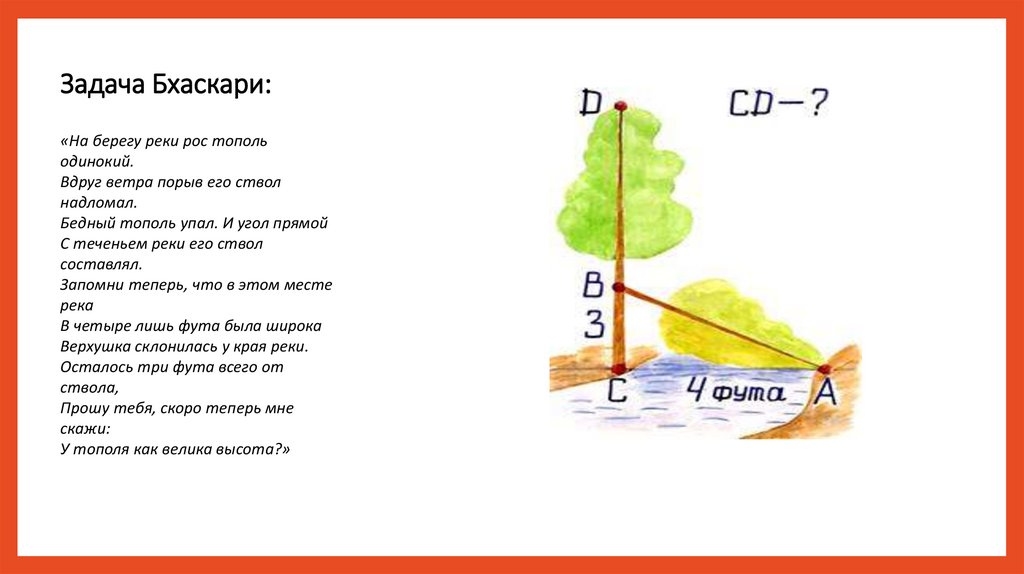
Задача Бхаскари:
«На берегу реки рос тополь
одинокий.
Вдруг ветра порыв его ствол
надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол
составлял.
Запомни теперь, что в этом месте
река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от
ствола,
Прошу тебя, скоро теперь мне
скажи:
У тополя как велика высота?»

32.

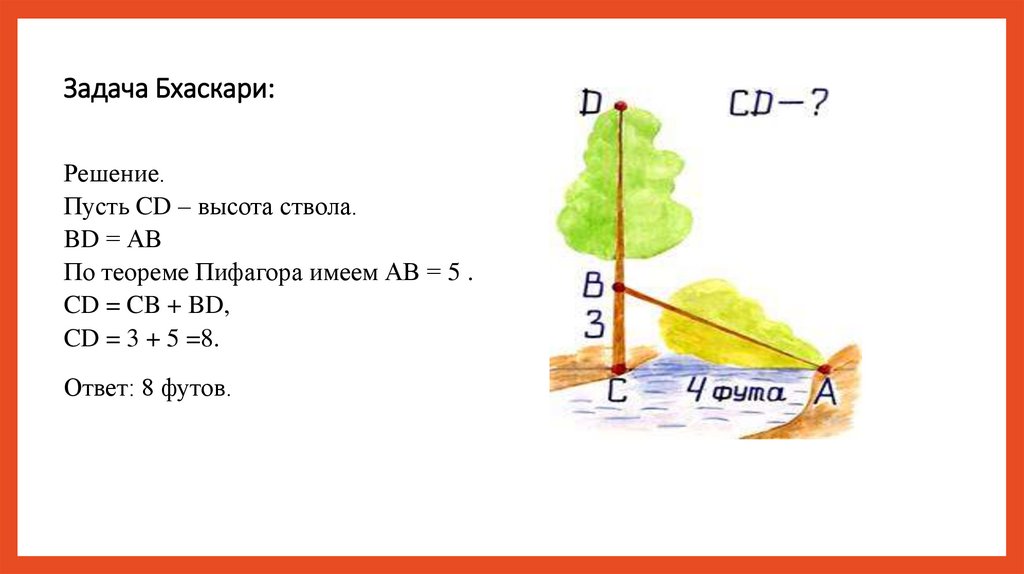
Задача Бхаскари:
Решение.
Пусть CD – высота ствола.
BD = АВ
По теореме Пифагора имеем АВ = 5 .
CD = CB + BD,
CD = 3 + 5 =8.
Ответ: 8 футов.

33.

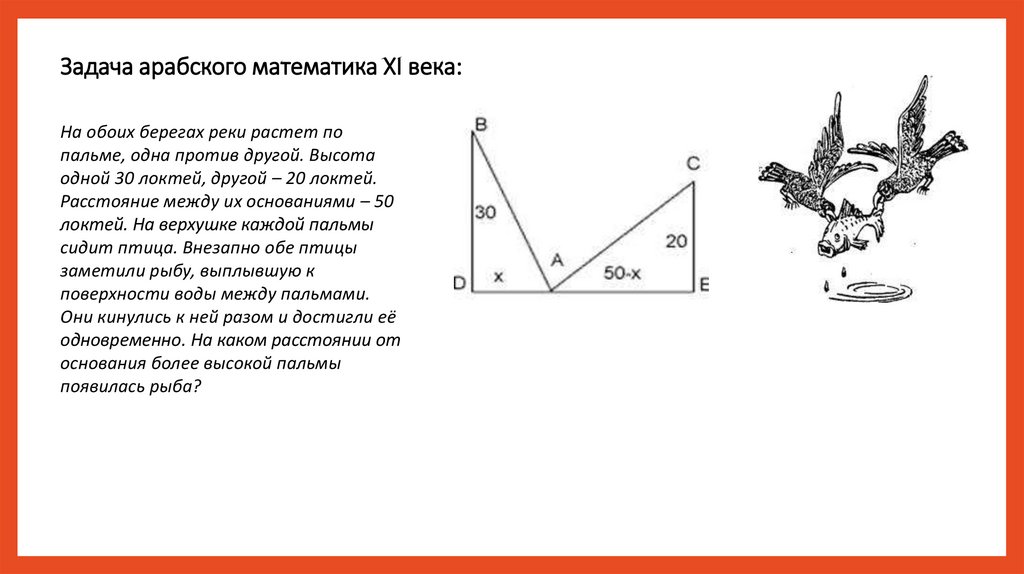
Задача арабского математика XI века:
На обоих берегах реки растет по
пальме, одна против другой. Высота
одной 30 локтей, другой – 20 локтей.
Расстояние между их основаниями – 50
локтей. На верхушке каждой пальмы
сидит птица. Внезапно обе птицы
заметили рыбу, выплывшую к
поверхности воды между пальмами.
Они кинулись к ней разом и достигли её
одновременно. На каком расстоянии от
основания более высокой пальмы
появилась рыба?

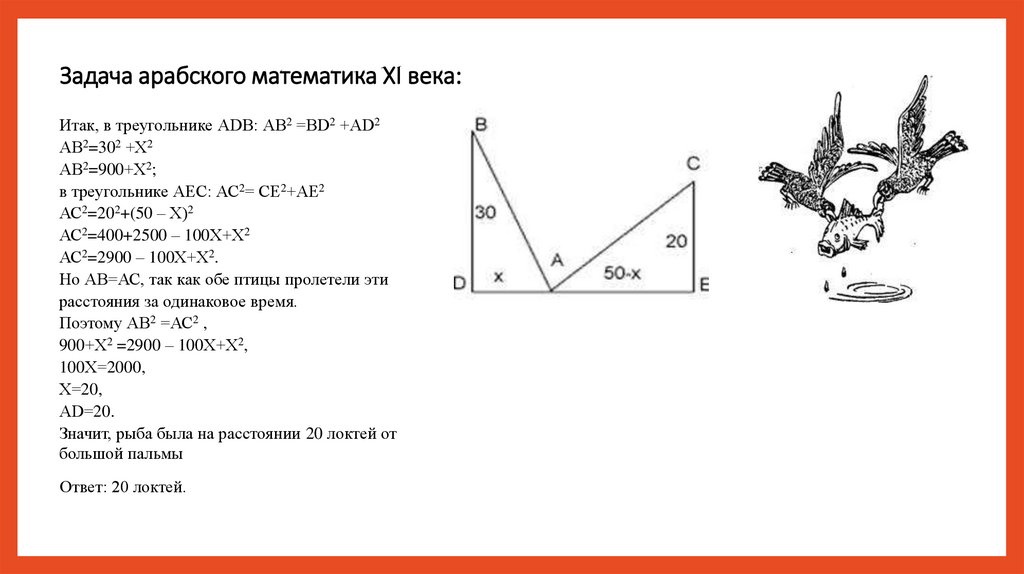
34.

Задача арабского математика XI века:
Итак, в треугольнике АDВ: АВ2 =ВD2 +АD2
АВ2=302 +Х2
АВ2=900+Х2;
в треугольнике АЕС: АС2= СЕ2+АЕ2
АС2=202+(50 – Х)2
АС2=400+2500 – 100Х+Х2
АС2=2900 – 100Х+Х2.
Но АВ=АС, так как обе птицы пролетели эти
расстояния за одинаковое время.
Поэтому АВ2 =АС2 ,
900+Х2 =2900 – 100Х+Х2,
100Х=2000,
Х=20,
АD=20.
Значит, рыба была на расстоянии 20 локтей от
большой пальмы
Ответ: 20 локтей.

35.

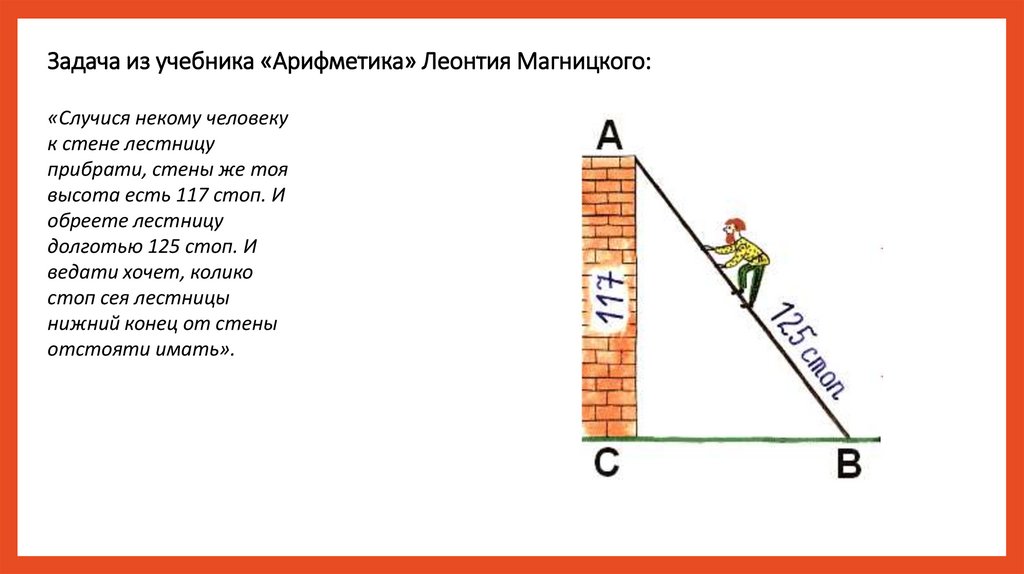
Задача из учебника «Арифметика» Леонтия Магницкого:
«Случися некому человеку
к стене лестницу
прибрати, стены же тоя
высота есть 117 стоп. И
обреете лестницу
долготью 125 стоп. И
ведати хочет, колико
стоп сея лестницы
нижний конец от стены
отстояти имать».

36.

ПРИМЕНЕНИЕ
ТЕОРЕМЫ ПИФАГОРА.

37.

Строительство.
Окно:
По теореме Пифагора имеем:
(b/4+p)=(b/4)+(b/4-p)
или
b/16+b*p/2+p=b/16+b/4-b*p+p,
откуда
b*p/2=b/4-b*p.
Разделив на b и приводя подобные
члены, получим:
(3/2)*p=b/4, p=b/6.

38.

Строительство.
Крыша:
Какой длины должны быть стропила, если изготовлены балки AC=8 м, и AB=BF.
Треугольник ADC - равнобедренный AB=BC=4 м, BF=4 м. Если предположить, что
FD=1,5 м, тогда:
А) Из треугольника DBC: DB=2,5м
DC=
Б)Из треугольника ABF:
AF=

39.

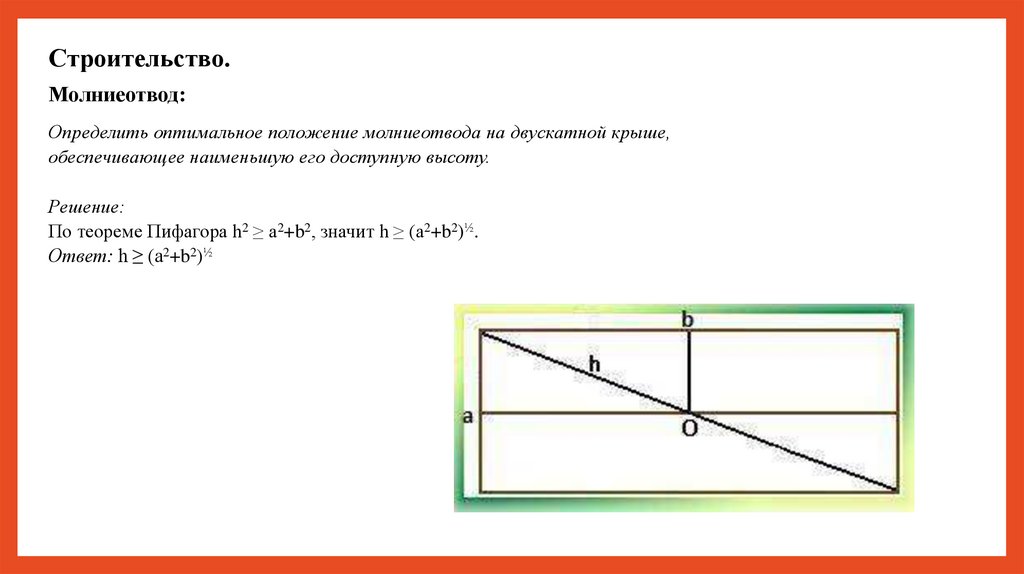
Строительство.
Молниеотвод:
Определить оптимальное положение молниеотвода на двускатной крыше,
обеспечивающее наименьшую его доступную высоту.
Решение:
По теореме Пифагора h2 ≥ a2+b2, значит h ≥ (a2+b2)½.
Ответ: h ≥ (a2+b2)½

40.

Мобильная связь.
Современные технологии.
Социальные сети.

41.

ПИФАГОРОВЫ
ТРОЙКИ.

42.

Пифагорова тройка- упорядоченный ряд чисел(x,y,z),
удовлетворяющий уравнению:
x^2+y^2=z^2

43.

упорядоченный ряд чисел(x,y,z), удовлетворяющий уравнению:
Пифагорова тройка- x^2+y^2=z^2
Примитивная-
Пифагорова тройка, которая не может быть получена способом,
названным ранее, из какой-то другой пифагоровой тройки, то
есть x, y и z являются взаимно простыми числами.

44.

Формула Евклида является основным средством построения пифагоровых троек. Согласно
ей для любой пары натуральных чисел
целые числа
образуют пифагорову тройку.
Тройки по формуле Евклида примитивны, когда m и n взаимно простые и (m-n)^m-n нечётно.

45.

Свойства пифагоровых троек:
Свойство 1. Числа, входящие в простейшую пифагорову тройку, попарно взаимно просты
Свойство 2. В простейшей пифагоровой тройке только одно число может быть чётным.
Свойство 3. В простейшей пифагоровой тройке числа x и y не могут быть одновременно нечётными.
Пифагоровы числа обладают рядом любопытных особенностей:
Один из катетов должен быть кратен трём.
Один из катетов должен быть кратен четырём.
Одно из пифагоровых чисел должно быть кратно пяти.

46.

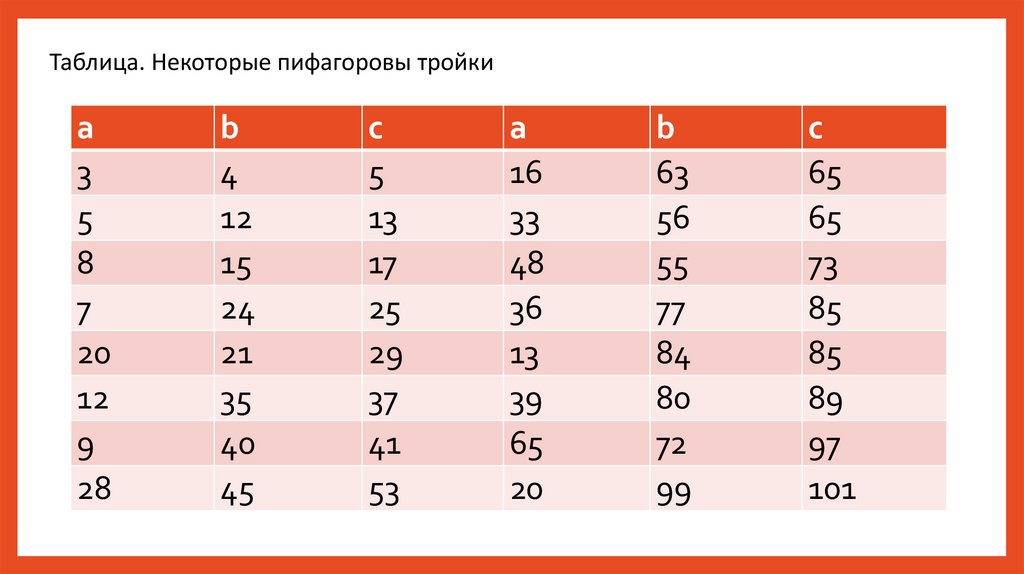
Таблица. Некоторые пифагоровы тройки
a
3
5
8
7
20
12
9
28
b
4
12
15
24
21
35
40
45
c
5
13
17
25
29
37
41
53
a
16
33
48
36
13
39
65
20
b
63
56
55
77
84
80
72
99
c
65
65
73
85
85
89
97
101

47.

РЕШЕНИЕ ЗАДАЧ С
ПОМОЩЬЮ
ПИФАГОРОВЫХ ТРОЕК
(Учебник «Геометрия 7 8 9» Л.С. Атанасян).

48.

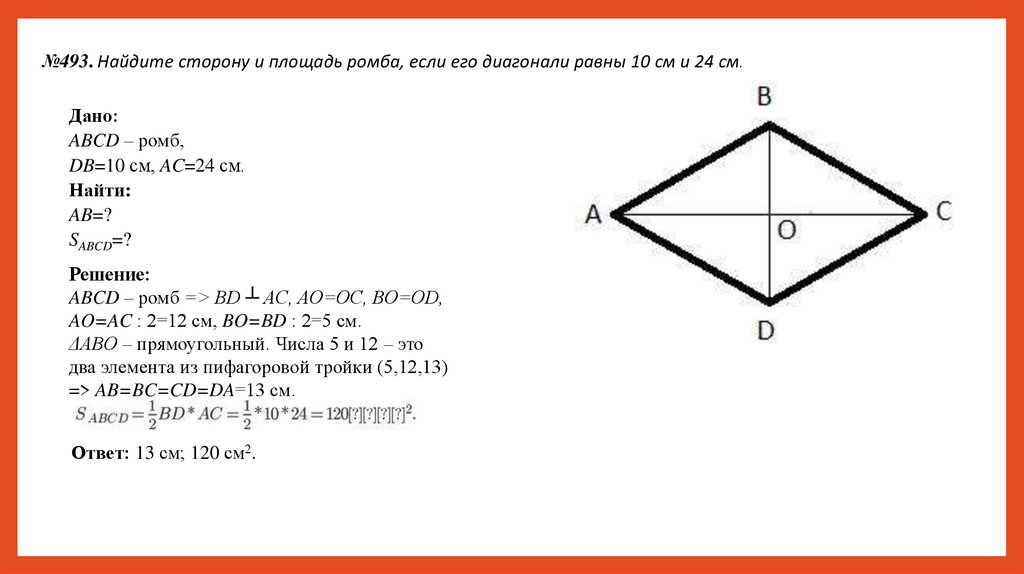
№493. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.
Дано:
ABCD – ромб,
DB=10 см, AC=24 см.
Найти:
AB=?
SABCD=?
Решение:
ABCD – ромб => BD ┴ AC, AO=OC, BO=OD,
AO=AC : 2=12 см, BO=BD : 2=5 см.
ΔABO – прямоугольный. Числа 5 и 12 – это
два элемента из пифагоровой тройки (5,12,13)
=> AB=BC=CD=DA=13 см.
Ответ: 13 см; 120 см2.

49.

№498. Выясните, является ли треугольник прямоугольным, если его стороны выражаются числами: а) 6,8,10;
б) 5,6,7; в) 9,12,15; г) 10,24,26; д) 3,4,6; е) 11,9,13; ж) 15,20,25. В каждом случае ответ обоснуйте.
а) Числа 6,8,10 имеют общий делитель 2. Разделив получаем пифагорову тройку (3,4,5) => треугольник
является прямоугольным.
б) Числа 5,6,7 не являются пифагоровой тройкой. Значит треугольник не прямоугольный.
в) Числа 9,12,15 не являются пифагоровой тройкой. Значит треугольник не прямоугольный.
г) Числа 10,24,26 имеют общий делитель 2. Разделив получаем пифагорову тройку (5,12,13) => треугольник
является прямоугольным.
д) Числа 3,4,6 не являются пифагоровой тройкой. Значит треугольник не прямоугольный.

50.

Общий вывод работы:
Теорема Пифагора – одна из важнейших теорем
геометрии;
На ее основании решается множество задач геометрии;
Теорема имеет большое практическое значение при
расчетах в архитектуре , строительстве, физике,
астрономии и т.д.;

51.

Спасибо за внимание!