Похожие презентации:
Тригонометрические неравенства и методы их решения
1.
Тригонометрическиенеравенства
и методы их решения
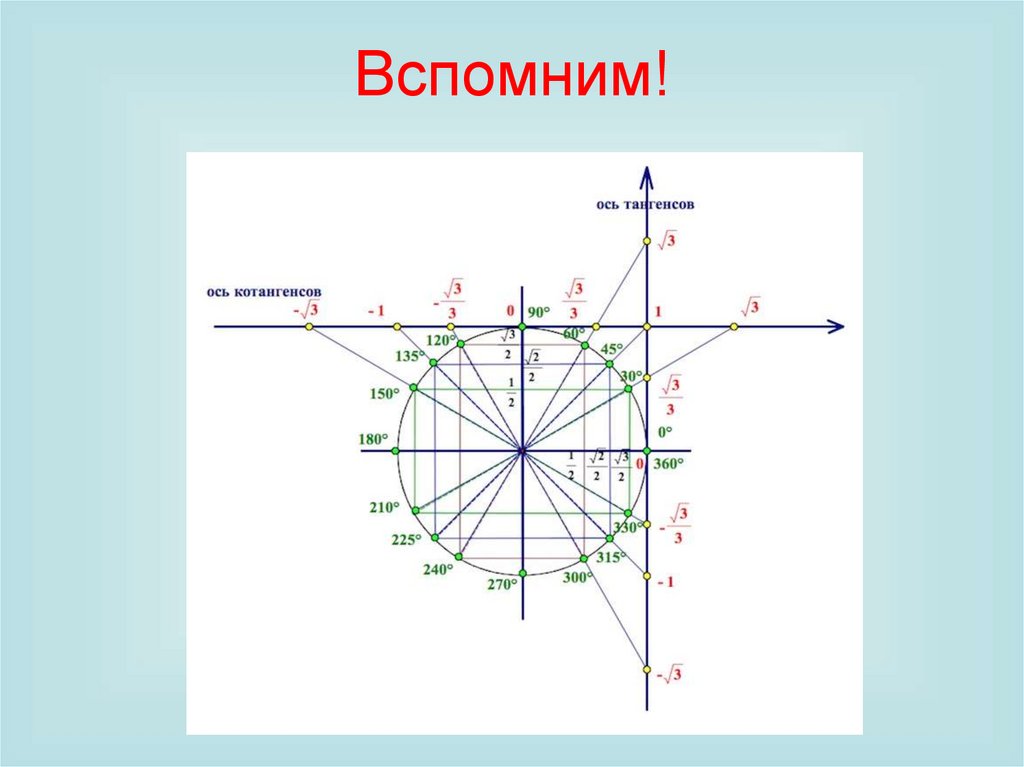
2. Вспомним!
3.
Вспомним!4.
Тригонометрическое неравенство - этонеравенство, содержащее переменную в
аргументе тригонометрической функции.
Решить тригонометрическое
неравенство - это значит, найти
множество значений неизвестных,
входящих в неравенство, при которых
неравенство выполняется.
5.
Тригонометрические неравенства можнорешать с помощью графиков
функций y = sin x, y = cos x, y = tg x,
y= ctg x или с помощью единичной
окружности.
Решение тригонометрических
неравенств, сводится, как правило, к
решению простейших неравенств вида:
sin x>a, sin x≥a, sin x≤a, sin x<a, cos x<a
и т. п.
6.
Алгоритм решения тригонометрическихнеравенств с помощью единичной
окружности:
1) На оси ординат (абсцисс) отметить точку a и провести
прямую y = a (x = a), перпендикулярную соответствующей оси
(точки пересечения можно соединить с центром окружности).
2) Отметить на окружности дугу, состоящую из точек окружности,
удовлетворяющих данному неравенству (эти точки расположены
по одну сторону от построенной прямой).
3) Выбрать положительный обход дуги ( против часовой стрелки)
4) Записать числовой промежуток, точки которого заполняют
отмеченную дугу, учитывая, что начало дуги –меньшее
значение, и к обеим частям неравенства прибавить период
функции ( для y = sin x и y = cos x T=2πn, для y = tg x, y= ctg x T=
πn).
7.
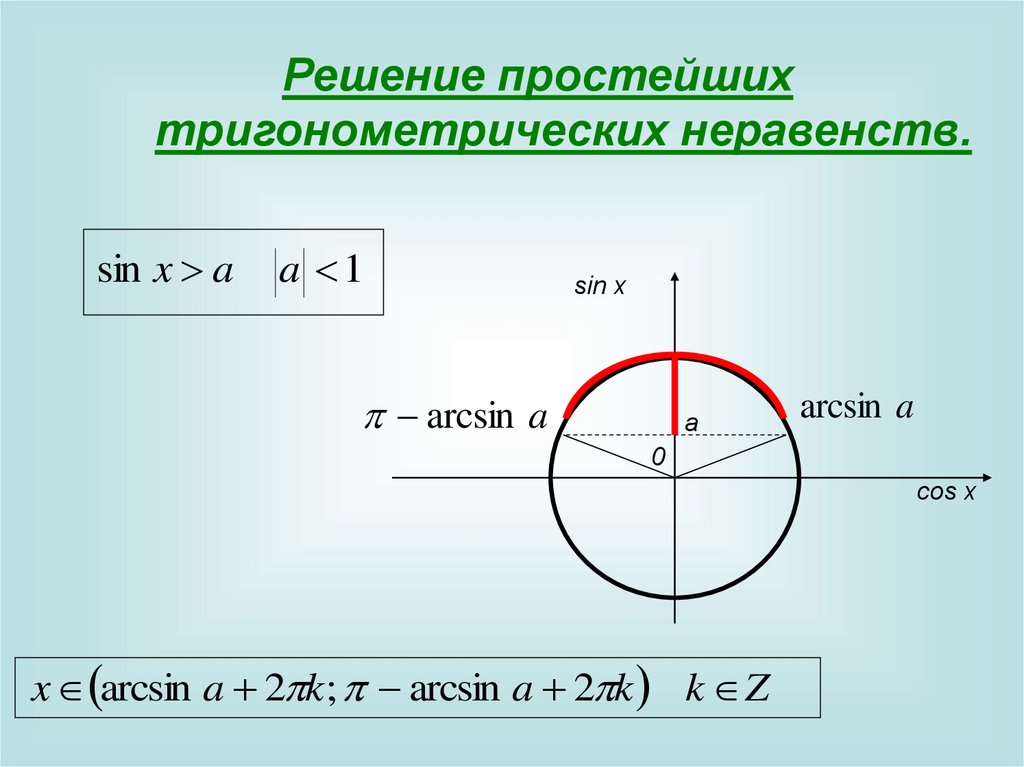
Решение простейшихтригонометрических неравенств.
sin x a
a 1
sin x
arcsin a
a
arcsin a
0
cos x
x arcsin a 2 k; arcsin a 2 k k Z
8.
Решение простейшихтригонометрических неравенств.
sin x a
a 1
sin x
arcsin a
a
arcsin a
0
cos x
x arcsin a 2 k; arcsin a 2 k k Z
9.
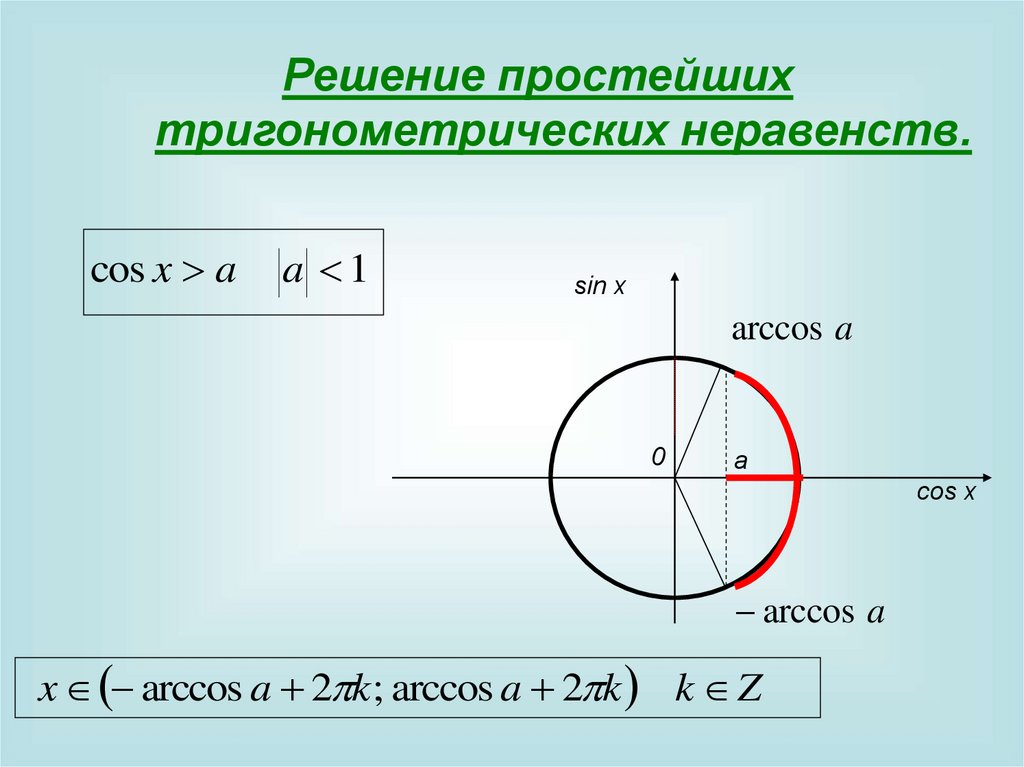
Решение простейшихтригонометрических неравенств.
cos x a
a 1
sin x
arccos a
0
a
cos x
arccos a
x arccos a 2 k; arccos a 2 k k Z
10.
Решение простейшихтригонометрических неравенств.
cos x a
a 1
sin x
arccos a
0
a
cos x
2 arccos a
x arccos a 2 k;2 arccos a 2 k k Z
11.
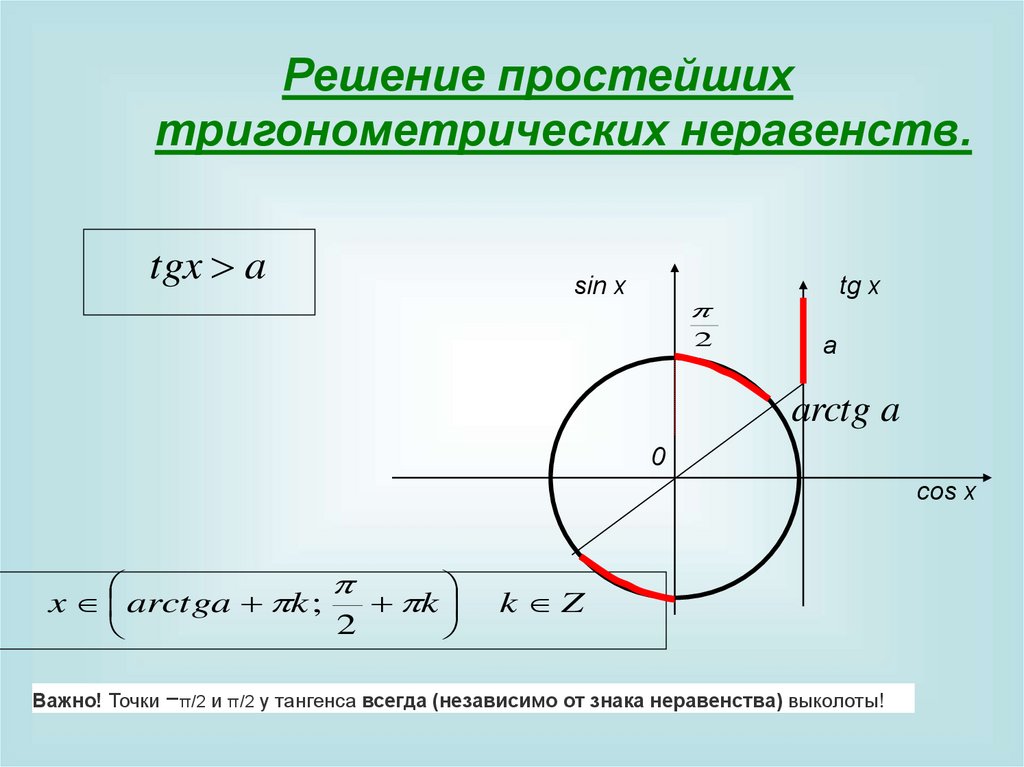
Решение простейшихтригонометрических неравенств.
tgx a
sin x
tg x
2
a
arctg a
0
cos x
x arctga k ;
k
2
k Z
Важно! Точки −π/2 и π/2 у тангенса всегда (независимо от знака неравенства) выколоты!
12.
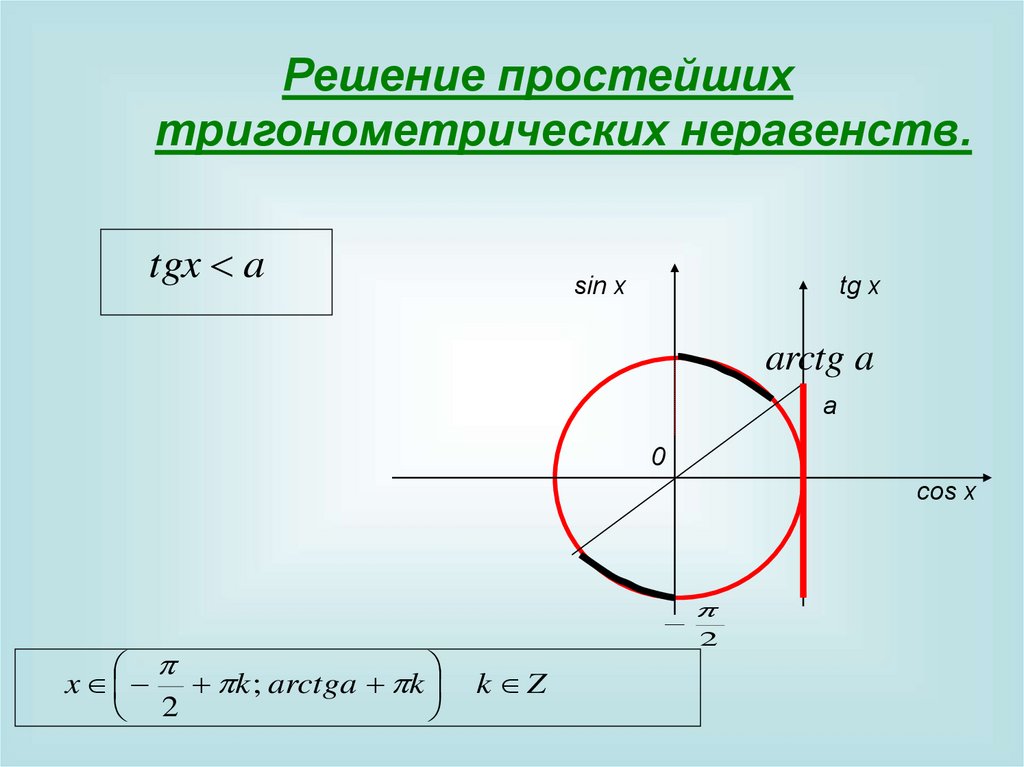
Решение простейшихтригонометрических неравенств.
tgx a
sin x
tg x
arctg a
a
0
cos x
x k ; arctga k
2
k Z
2
13.
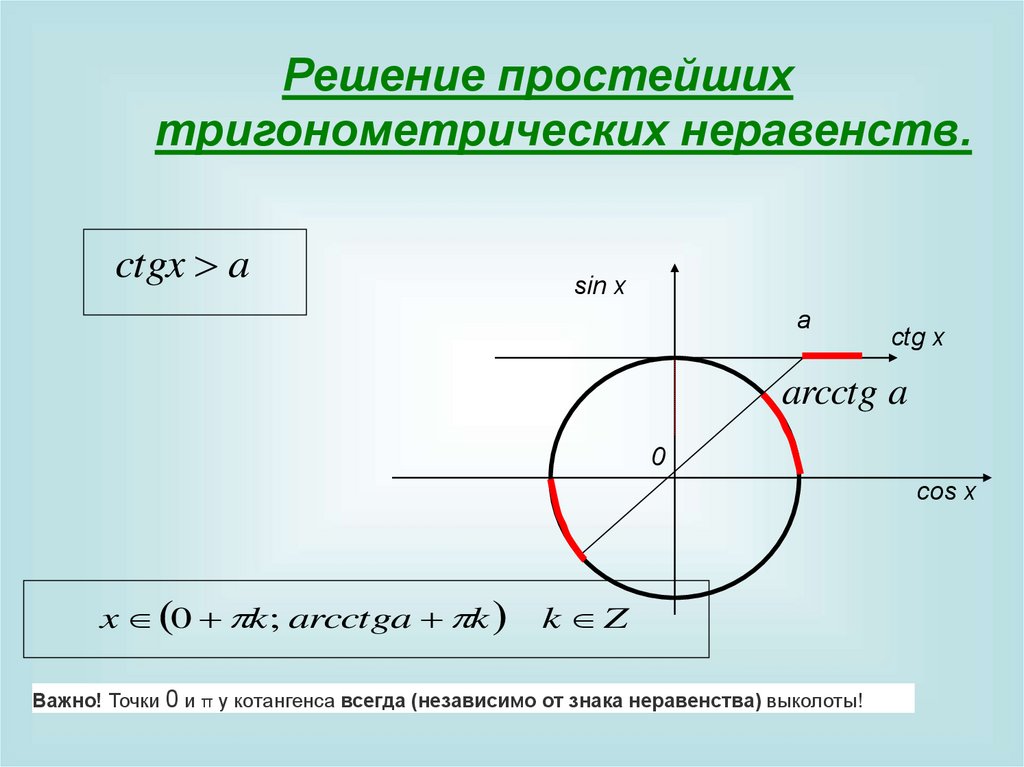
Решение простейшихтригонометрических неравенств.
ctgx a
sin x
a
сtg x
arcctg a
0
cos x
x 0 k ; arcctga k
k Z
Важно! Точки 0 и π у котангенса всегда (независимо от знака неравенства) выколоты!
14.
Решение простейшихтригонометрических неравенств.
ctgx a
sin x
a
сtg x
arcctg a
0
cos x
x arcctga k; k k Z
15. Примеры решений тригонометрических неравенств
16.
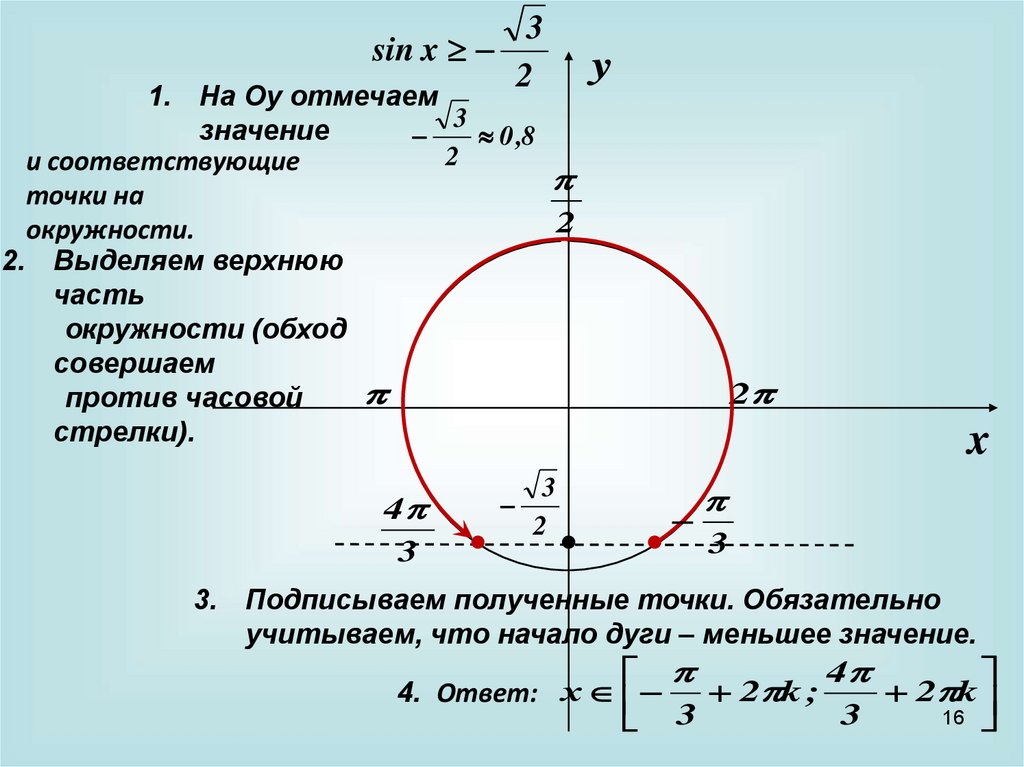
32
sin x
1. На Оу отмечаем
3
значение
0 ,8
2
и соответствующие
точки на
2
окружности.
2. Выделяем верхнюю
часть
окружности (обход
совершаем
против часовой
стрелки).
4
3
3
2
y
2
x
3
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
4
2 k ;
2 k
4. Ответ: х
3
16
3
17.
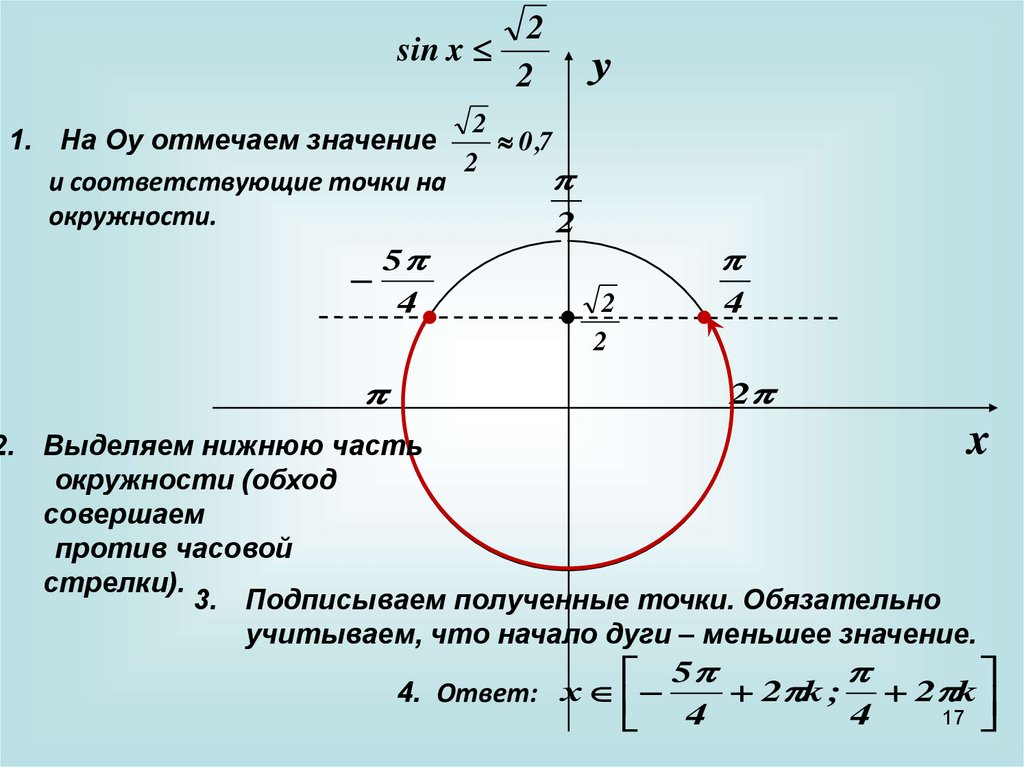
sin x2
2
y
2
1. На Оу отмечаем значение
0 ,7
2
и соответствующие точки на
окружности.
2
5
4
2
2
4
2
x
2. Выделяем нижнюю часть
окружности (обход
совершаем
против часовой
стрелки).
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
5
2 k ; 2 k
4. Ответ: х
4
4
17
18.
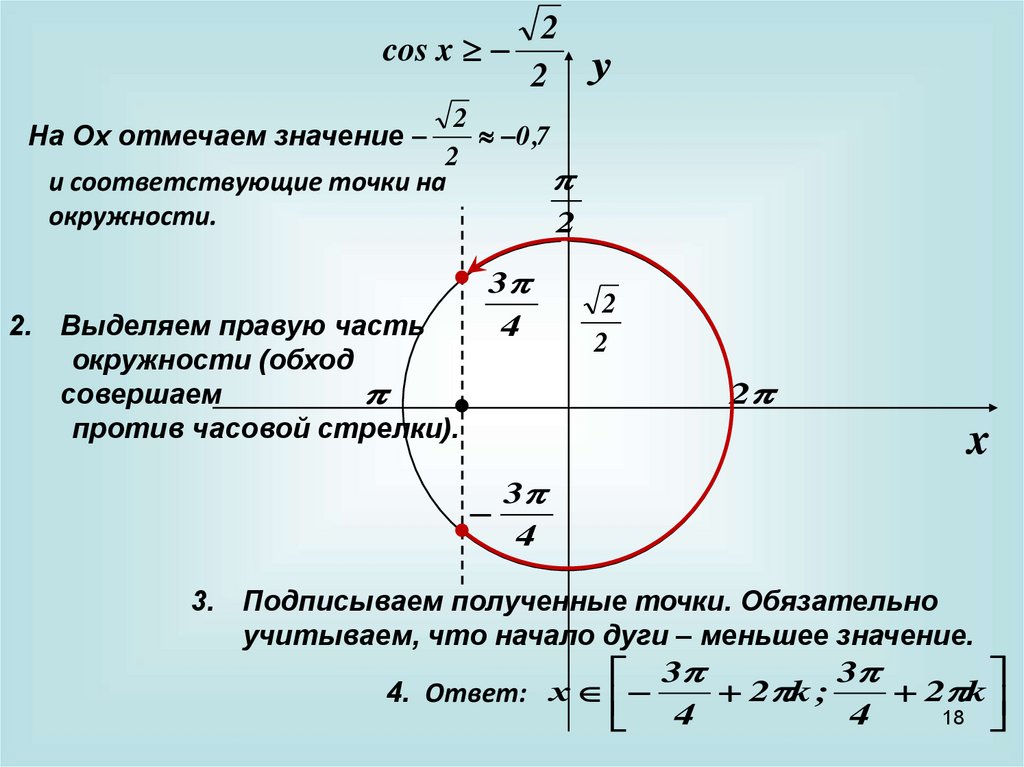
cos x2
2 y
2
0 ,7
2
и соответствующие точки на
окружности.
2
. На Ох отмечаем значение
2. Выделяем правую часть
окружности (обход
совершаем
против часовой стрелки).
3
4
2
2
2
x
3
4
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
3
3
2 k ;
2 k
4. Ответ: х
4
4
18
19.
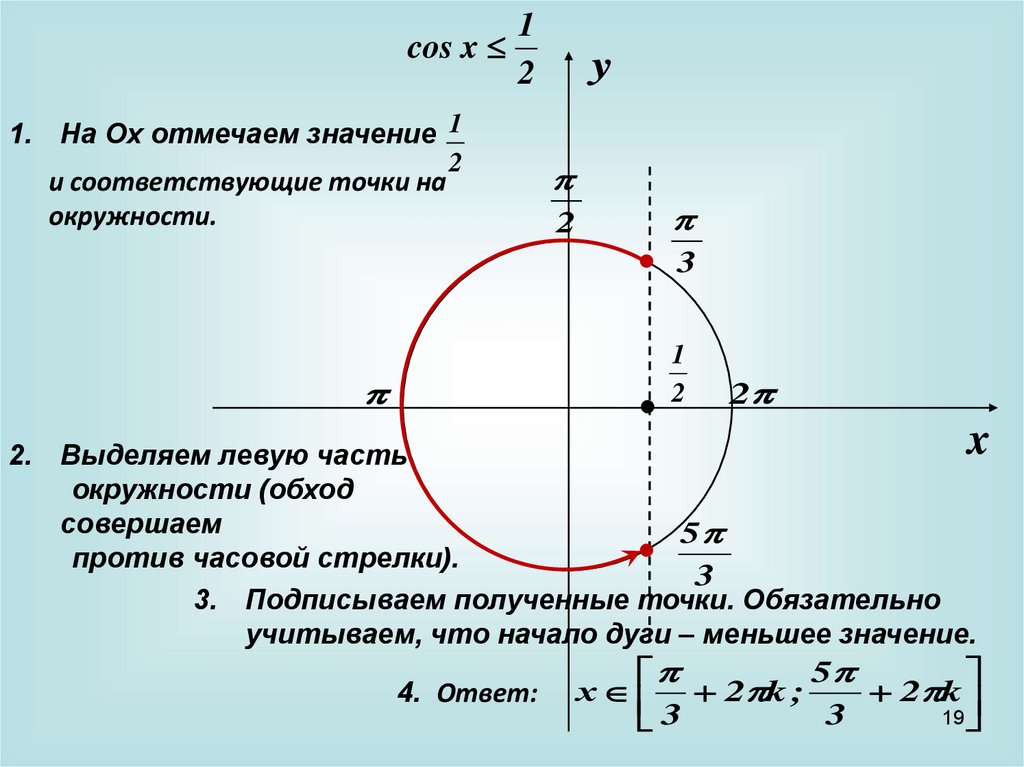
1cos x
2
1. На Оx отмечаем значение 1
2
и соответствующие точки на
окружности.
y
2
3
1
2
2
x
2. Выделяем левую часть
окружности (обход
совершаем
5
против часовой стрелки).
3
3. Подписываем полученные точки. Обязательно
учитываем, что начало дуги – меньшее значение.
4. Ответ:
5
х 2 k ;
2 k
3
19
3
20.
23
2
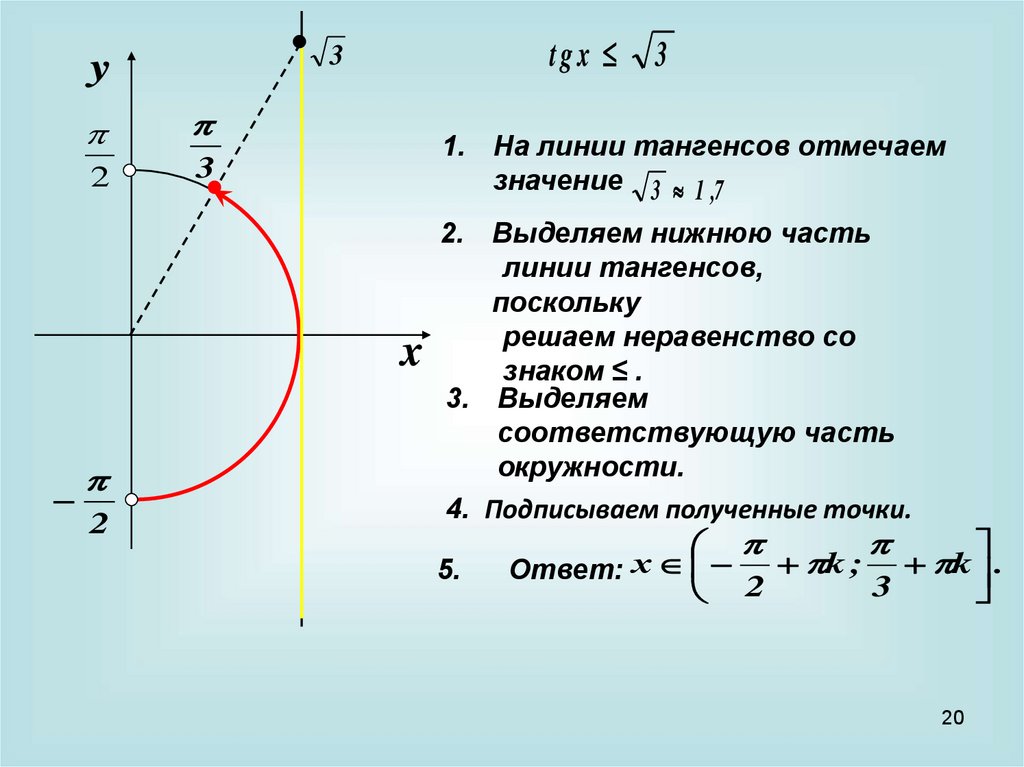
tgx
3
y
3
1. На линии тангенсов отмечаем
значение 3 1 ,7
2. Выделяем нижнюю часть
линии тангенсов,
поскольку
решаем неравенство со
x
знаком ≤ .
3. Выделяем
соответствующую часть
окружности.
4. Подписываем полученные точки.
5.
х
k
;
k
.
Ответ:
3
2
20
21.
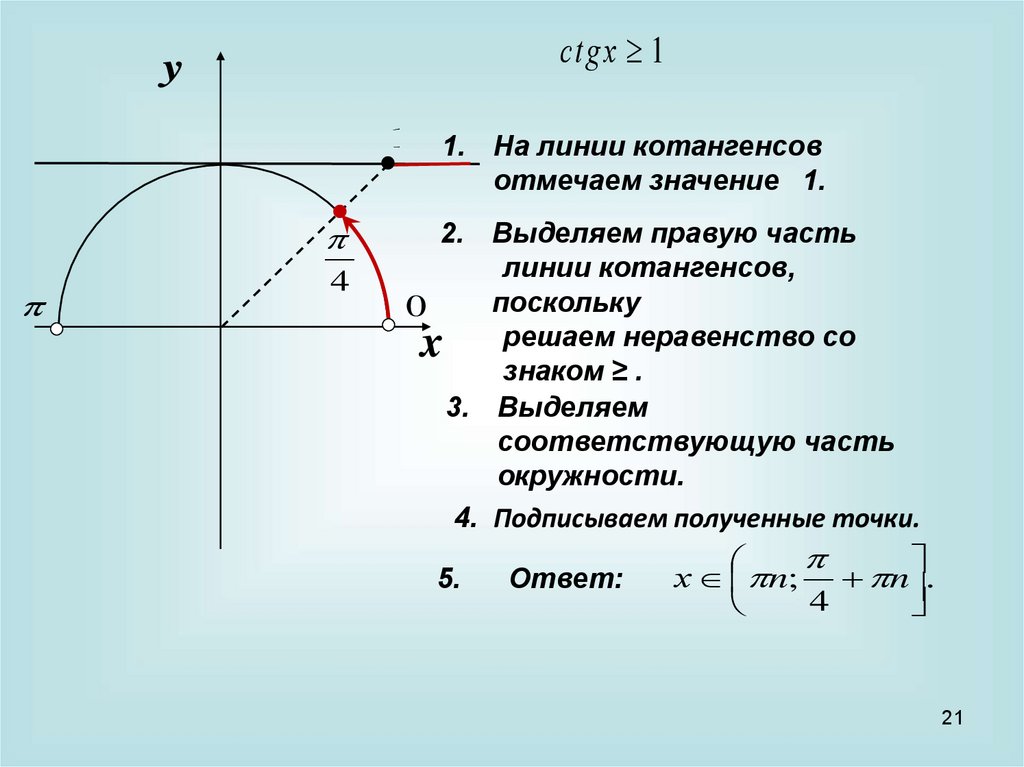
сtgx 1y
1 1. На линии котангенсов
отмечаем значение 1.
4
2. Выделяем правую часть
линии котангенсов,
поскольку
0
x решаем неравенство со
знаком ≥ .
3. Выделяем
соответствующую часть
окружности.
4. Подписываем полученные точки.
5.
Ответ:
х n; n .
4
21









 Математика
Математика








