Похожие презентации:
Переменный ток. Лекция №2
1.
ПЕРЕМЕННЫЙ ТОКЛекция № 2
2.
Преимущества и недостаткипеременного тока
• Проще (с помощью трансформатора) изменять рабочее
напряжение
• Возможность получения источников электрической энергии
большой мощности
• Возможность повышения КПД при передаче электроэнергии на
большие расстояния за счёт повышения напряжения ЛЭП
• Двигатели переменного тока (в частности, асинхронные
двигатели, в которых отсутствуют движущиеся электрические
контакты) проще и дешевле двигателей постоянного тока
• А недостатками переменного тока являются потери, связанные с
излучением электромагнитных волн и наведенными в
окружающих предметах токами, проблема реактивных токов,
сложность сложения мощностей разных генераторов (нужно,
чтобы они работали строго на одной частоте), повышенная
нагрузка на диэлектрики, а при относительно низких (бытовых)
напряжениях - - еще и повышенная опасность.
3.
Преимущества и недостаткипостоянного тока
• Преимущества постоянного тока, это зеркальное отражение
недостатков переменного:
• На предельном напряжении передаваемая мощность
постоянного тока в 2 раза выше, чем переменного.
• При наличии нескольких генераторов в сети, не требуется их
согласование по частоте и фазе (отсутствуют такие понятия у
постоянного тока), только по напряжению.
• Не важна индуктивность и емкость линии.
• Пропускная способность линий ограничена только тепловым
пределом проводов.
• Не создаются помехи.
4.
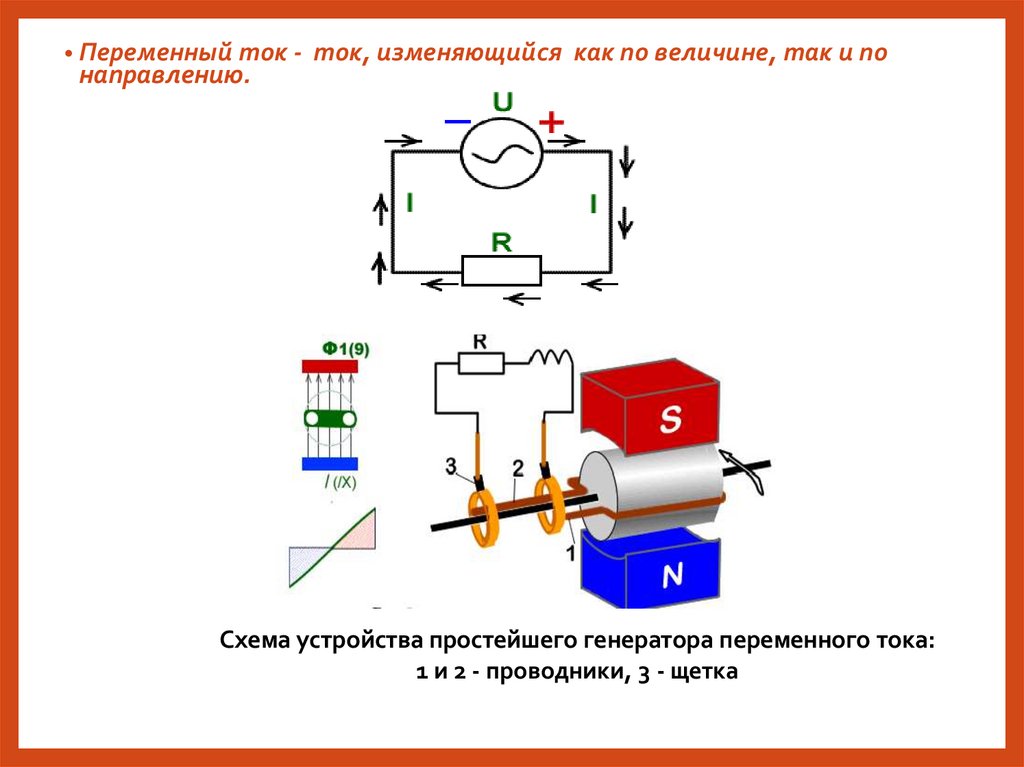
• Переменный ток - ток, изменяющийся как по величине, так и понаправлению.
Схема устройства простейшего генератора переменного тока:
1 и 2 - проводники, 3 - щетка
5.
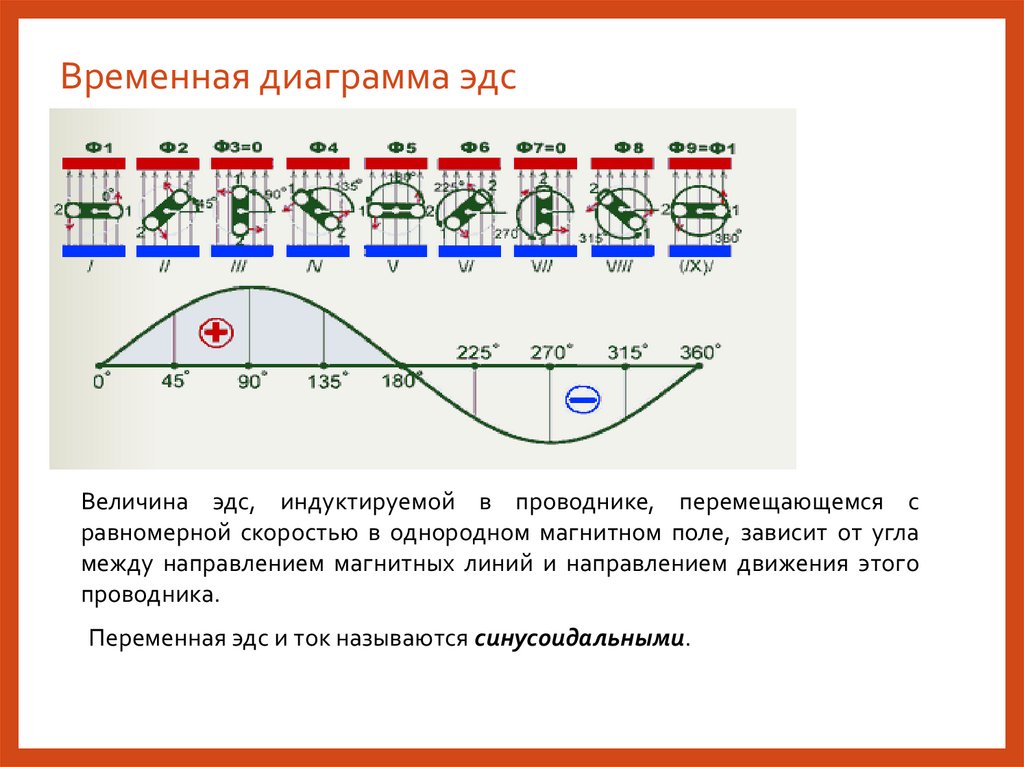
Временная диаграмма эдсВеличина эдс, индуктируемой в проводнике, перемещающемся с
равномерной скоростью в однородном магнитном поле, зависит от угла
между направлением магнитных линий и направлением движения этого
проводника.
Переменная эдс и ток называются синусоидальными.
6.
e = Blv sinα. При α=90° Em =Blvе = Еm sinα, угол α – фаза
Часть эдс, которая уравновешивается во внешней цепи,
называют напряжением генератора и обозначают его
мгновенное значение буквой u, a максимальное
(амплитуду) — буквой Um.
Соотношение между электрическими величинами и их
взаимное расположение на плоскости, выраженное
графически в форме векторов, называется векторной
диаграммой.
Промежуток времени, необходимый для совершения
переменной эдс полного цикла своих изменений,
называется
периодом (T). Измеряется в с.
Число периодов в одну секунду
Частота
обозначается
f=1/Т
называется сокращенно частотой.
и
измеряется
в
герцах
(Гц).
Угловая частота равна: ω=2 π /Т .
Фаза α=ωπ/Т
..\
7.
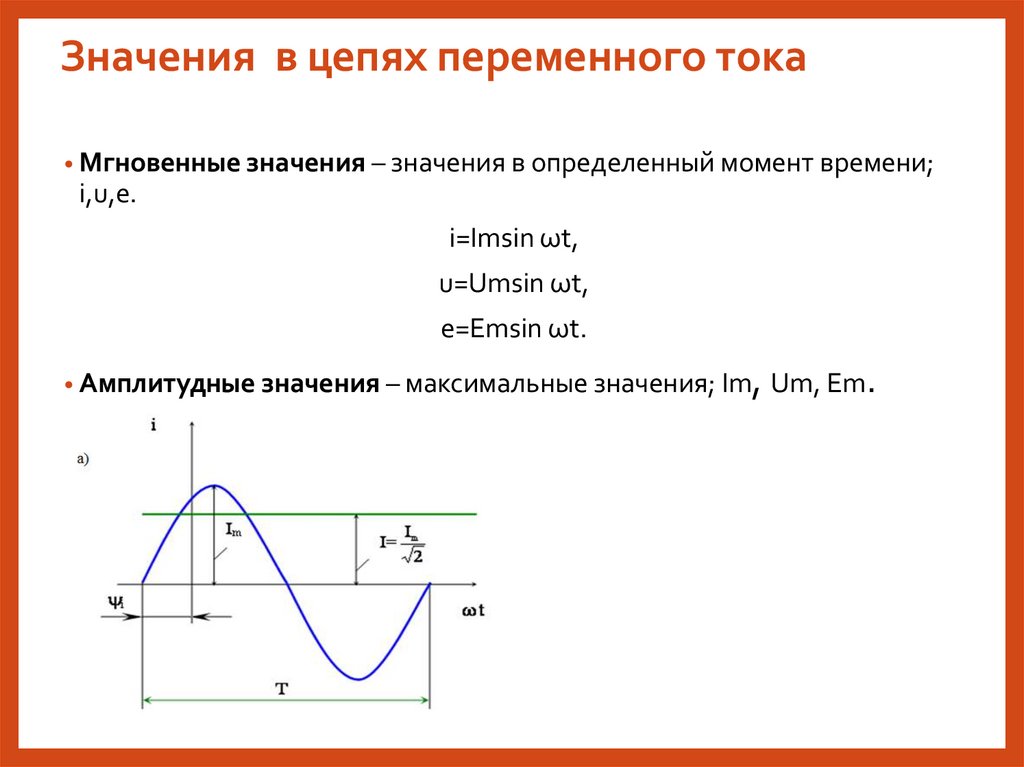
Значения в цепях переменного тока• Мгновенные значения – значения в определенный момент времени;
i,u,e.
i=Imsin ωt,
u=Umsin ωt,
e=Emsin ωt.
, Um, Em.
• Амплитудные значения – максимальные значения; Im
8.
Действующее значение переменного тока равно по величине такомузначению постоянного тока, который, протекая по такому же
сопротивлению, что и переменный ток , за один и тот же промежуток
времени выделяет одинаковое количество тепла.
Вольтметры и амперметры показывают действующие значения.
I = Im/√ 2 = 0.707.
Аналогично: U=Um/√2=0.707Um,
E=Em/√2=0.707Um.
Среднее значение синусоидальной величины за период равно нулю.
Поэтому за среднее значение берется среднее значение за полупериод
Iср=2Im/π,
Uср=2Um/π,
Eср=2Em/π.
9.
Расчет цепей переменного токаЛюбому вектору , расположенному на комплексной
плоскости, соответствует комплексное число , которое
может быть записано в трех формах: алгебраической,
тригонометрической и показательной.
В электротехнике от математики мнимую единицу
обозначают j.
• Алгебраическая форма записи комплексного числа
А а1 jа 2
+j
А
a2
YA>0
a1
где а1- проекция вектора на ось
действительных чисел (+1,Re);
а2- проекция вектора на ось мнимых
чисел (+j,Jm).
+1
10.
• Тригонометрическая форма записиА А cos A jA sin A
где А – длина вектора;
действительных чисел
A- угол наклона вектора к оси
•Показательная форма записи
A Ae
j A
где А – модуль комплексного числа (соответствует действующему
значению синусоидальной функции или длине вектора);
A - аргумент комплексного числа (соответствует углу наклона
вектора к оси действительных
синусоидальной функции);
чисел
или
начальной
фазе
Комплексные числа A и А
называются сопряженными, если их
модули равны, а аргументы равны и противоположны по знаку
11.
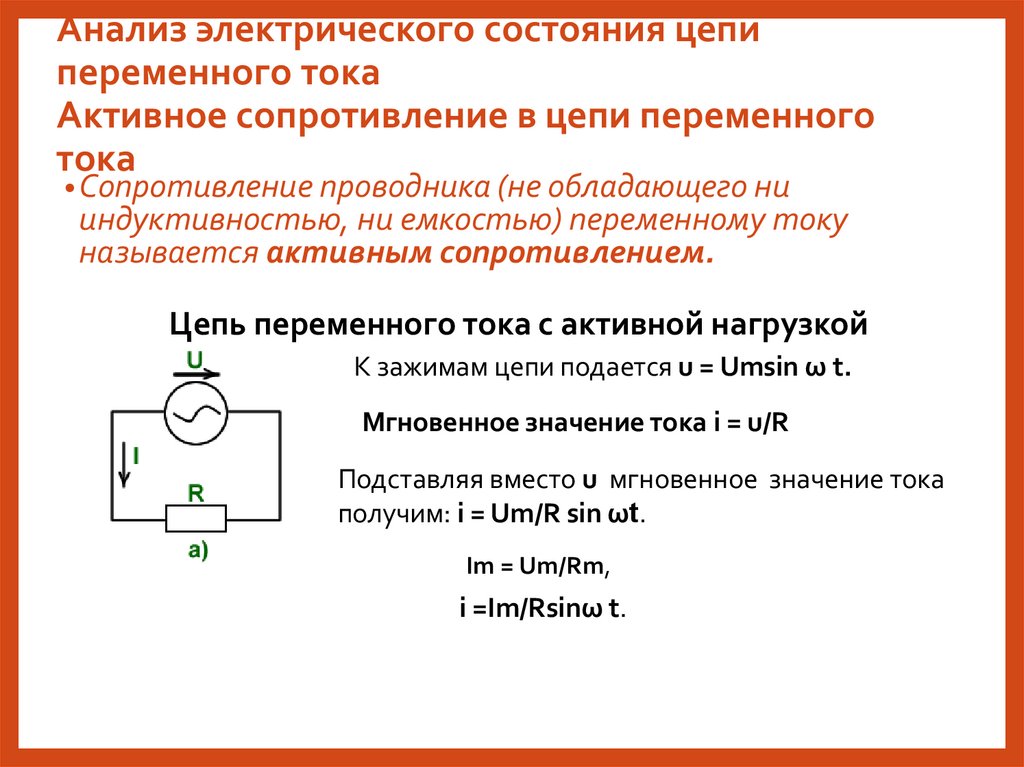
Анализ электрического состояния цепипеременного тока
Активное сопротивление в цепи переменного
тока
• Сопротивление проводника (не обладающего ни
индуктивностью, ни емкостью) переменному току
называется активным сопротивлением.
Цепь переменного тока с активной нагрузкой
К зажимам цепи подается u = Umsin ω t.
Мгновенное значение тока i = u/R
Подставляя вместо u мгновенное значение тока
получим: i = Um/R sin ωt.
Im = Um/Rm,
i =Im/Rsinω t.
12.
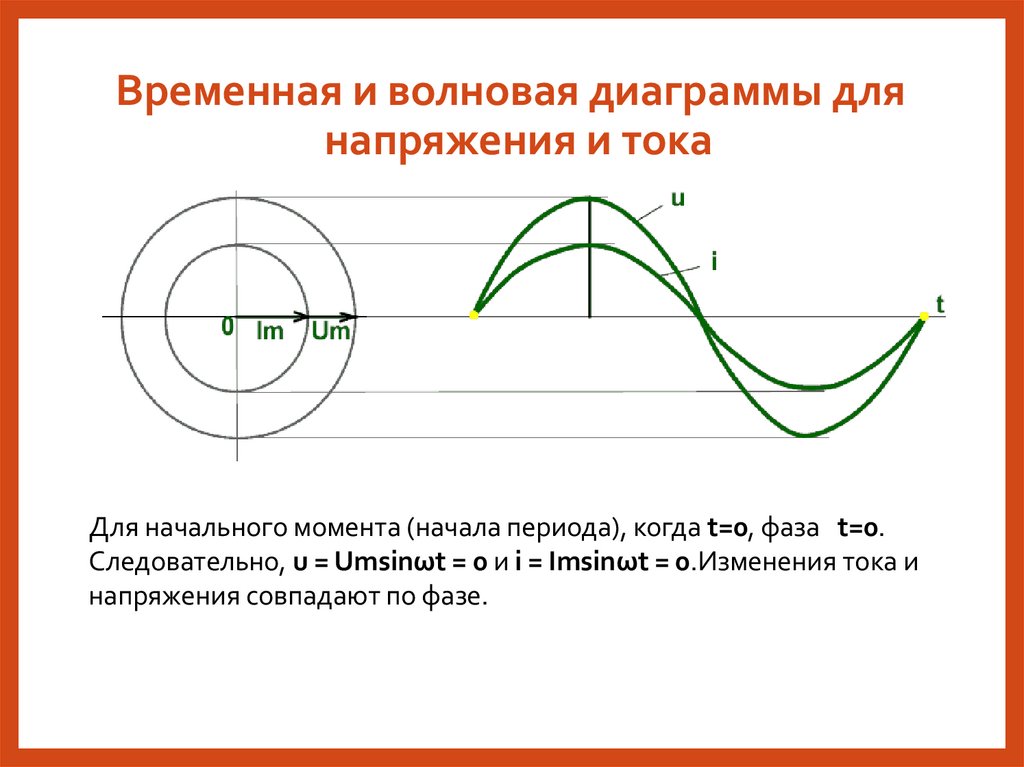
Временная и волновая диаграммы длянапряжения и тока
Для начального момента (начала периода), когда t=0, фаза t=0.
Следовательно, u = Umsinωt = 0 и i = Imsinωt = 0.Изменения тока и
напряжения совпадают по фазе.
13.
Катушка индуктивности в цепипеременного тока
Индуктивный
элемент
характеризуется
преобразованием электрической энергии в
энергию магнитного поля при нарастании
тока и обратным преобразованием энергии
магнитного поля в электрическую энергию
при убывании тока.
di
Эдс самоиндукции
eL . L
dt
eL ELm sin( t 2),
После дифференцирования
где E Lm LI-mамплитуда эдc самоиндукции,
индуктивное сопротивление
L 2 fL X L
14.
,di
u eL L U Lm
dt
где U Lm LI m- амплитуда напряжения
В цепи с индуктивностью напряжение опережает ток по фазе на угол /2.
В комплексной форме
Закон Ома в комплексной форме:
U Ue
j90
UL
UL
I
jX L j L
где jX L j L- комплексное индуктивное сопротивление
15.
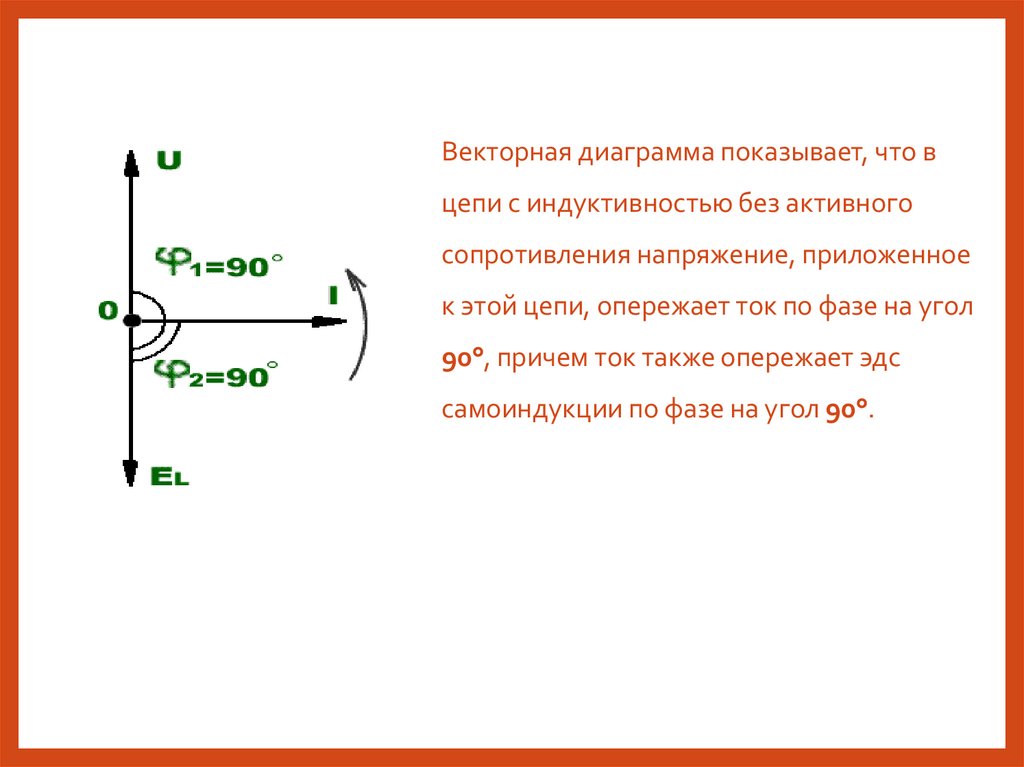
Векторная диаграмма показывает, что вцепи с индуктивностью без активного
сопротивления напряжение, приложенное
к этой цепи, опережает ток по фазе на угол
90°, причем ток также опережает эдс
самоиндукции по фазе на угол 90°.
16.
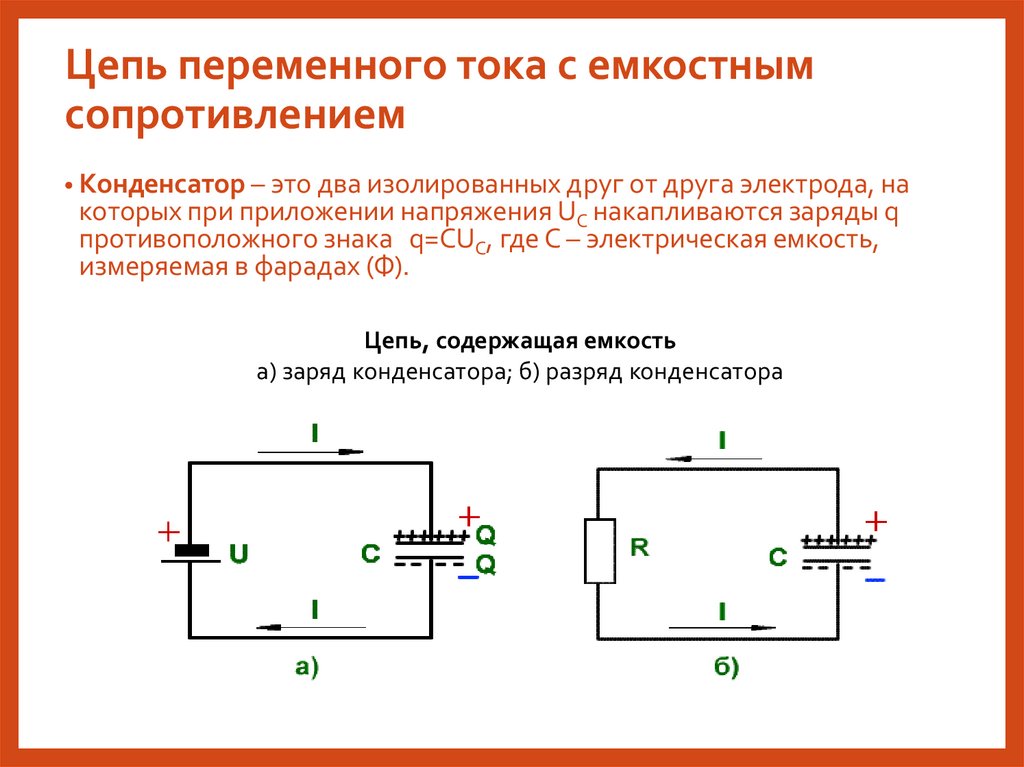
Цепь переменного тока с емкостнымсопротивлением
• Конденсатор – это два изолированных друг от друга электрода, на
которых при приложении напряжения UC накапливаются заряды q
противоположного знака q=CUC, где C – электрическая емкость,
измеряемая в фарадах (Ф).
Цепь, содержащая емкость
а) заряд конденсатора; б) разряд конденсатора
17.
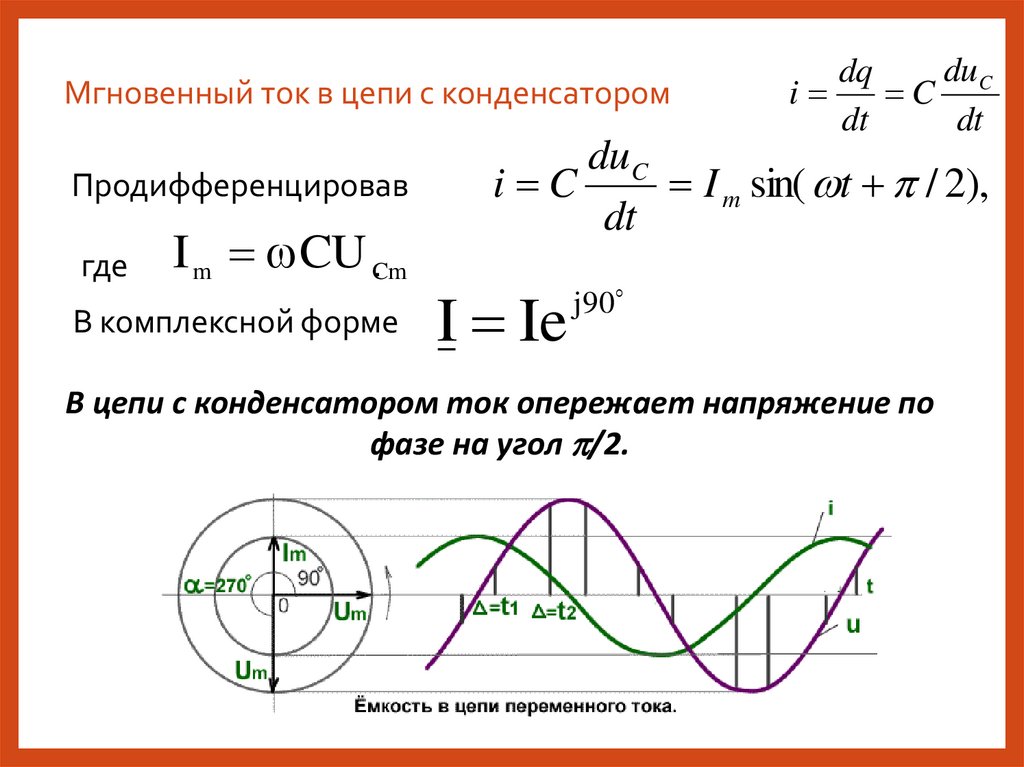
Мгновенный ток в цепи с конденсаторомПродифференцировав
где
I m CU C. m
В комплексной форме
duC
dq
i
C
dt
dt
duC
i C
I m sin( t / 2),
dt
I Ie
j90
В цепи с конденсатором ток опережает напряжение по
фазе на угол /2.
18.
11
XC
C 2 fC
Емкостное сопротивление
Закон Ома в комплексной форме:
UC
I
jX C
Закон Ома для действующих значений I U C U C
C
XC
I
Векторная диаграмма
2
UC
19.
Цепь с последовательным соединением элементов R, L, Ci
u
С
R
L
uR
uL
uC
u U m sin( t U )
i I m sin t i
По второму закону Кирхгофа
u uR uL uC
Для комплексных напряжений
U UR UL UC
закон Ома в комплексной форме:
U
U
I
R j X L X C Z
Где Z R j X L X C - комплексное
сопротивление
X X L X C – реактивное сопротивление.
20.
Модуль комплексного сопротивления (полное сопротивление)Z R (X L X C )
2
2
XL XC
arctg
– аргумент комплексного сопротивления
R
Треугольник сопротивлений
0 90
Если емкостное сопротивление в цепи больше индуктивного
,то нагрузка имеет активно-емкостный характер, то есть ток
по фазе опережает напряжение.
Если индуктивное сопротивление больше емкостного , то
нагрузка в цепи имеет активно-индуктивный характер; ток по
фазе отстает от напряжения на угол
21.
ХL > XCПо второму закону Кирхгофа:
U U R U L U C
Так как
UL > UC .
Х L > X,C то
U p U L UC -реактивная
Ua UR
напряжения
-активная
напряжения
составляющая
составляющая
22.
Порядок построения векторной диаграммыI
1.Cтроим вектор тока I ( при нулевой
начальной
фазе
он
расположен
горизонтально)
2. Cтроим вектор падения напряжения на
активном сопротивлении Ur (он совпадает по
направлению с вектором тока , сдвиг фаз
равен нулю)
3. Cтроим вектор падения напряжения на
индуктивном
сопротивлении
UL
(он
опережает по фазе вектор тока на 90 );
4. Cтроим вектор падения напряжения на
емкостном сопротивлении Uc (он отстает по
фазе от вектора тока на 90 );
5. Cкладывая векторы Ur, UL, Uc получаем
вектор общего напряжения U, который
опережает по фазе на угол > вектор тока ,
что указывает на активно-индуктивный
характер нагрузки.
23.
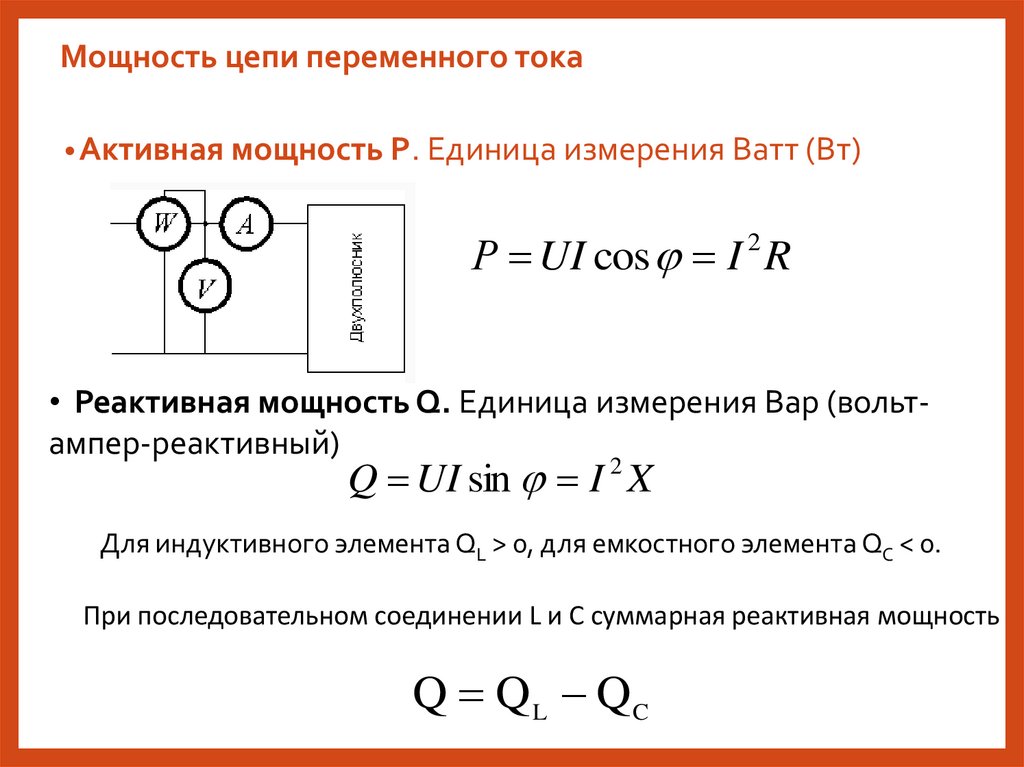
Мощность цепи переменного тока• Активная мощность Р. Единица измерения Ватт (Вт)
Р UI cos I 2 R
• Реактивная мощность Q. Единица измерения Вар (вольтампер-реактивный)
Q UI sin I 2 X
Для индуктивного элемента QL > 0, для емкостного элемента QC < 0.
При последовательном соединении L и C суммарная реактивная мощность
Q Q L QC
24.
• Полная мощность S. Единица измерения ВА (вольт-ампер)..
S UI P2 Q2
Треугольник мощностей
Q
arctg
P
S
Q = QL - QC
P
Р
cos = -коэффициент мощности.
S
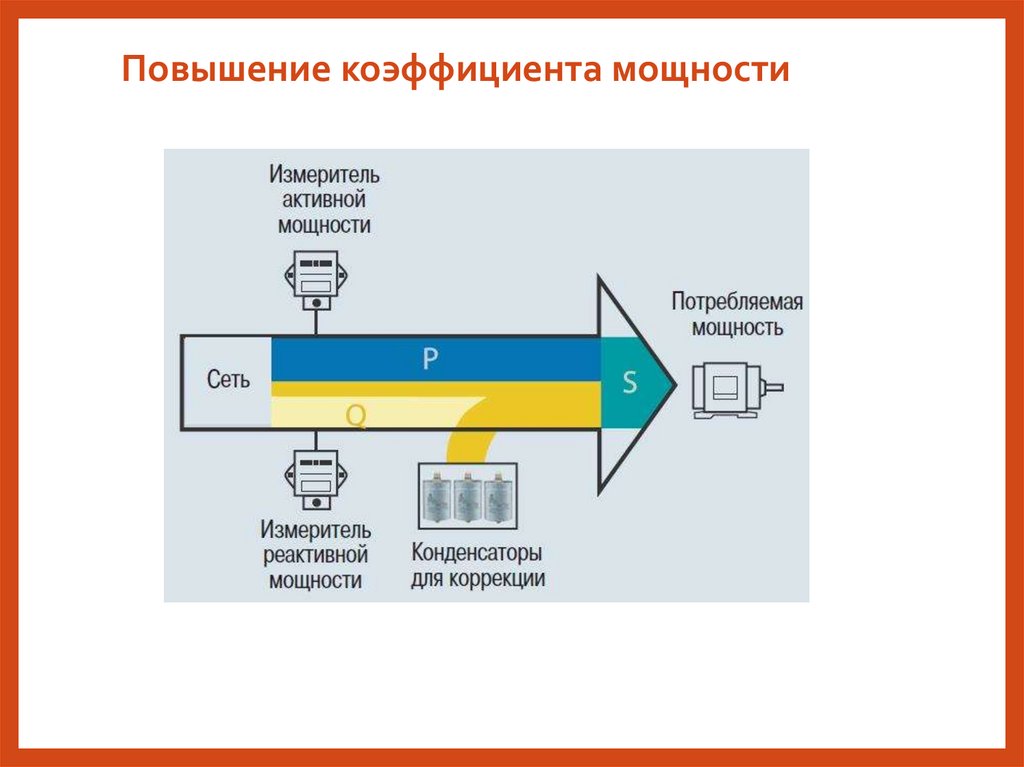
Коэффициент мощности показывает, какая часть электрической
энергии, потребляемой из сети, используется на выполнение полезной
работы.
25.
Повышение коэффициента мощности26.
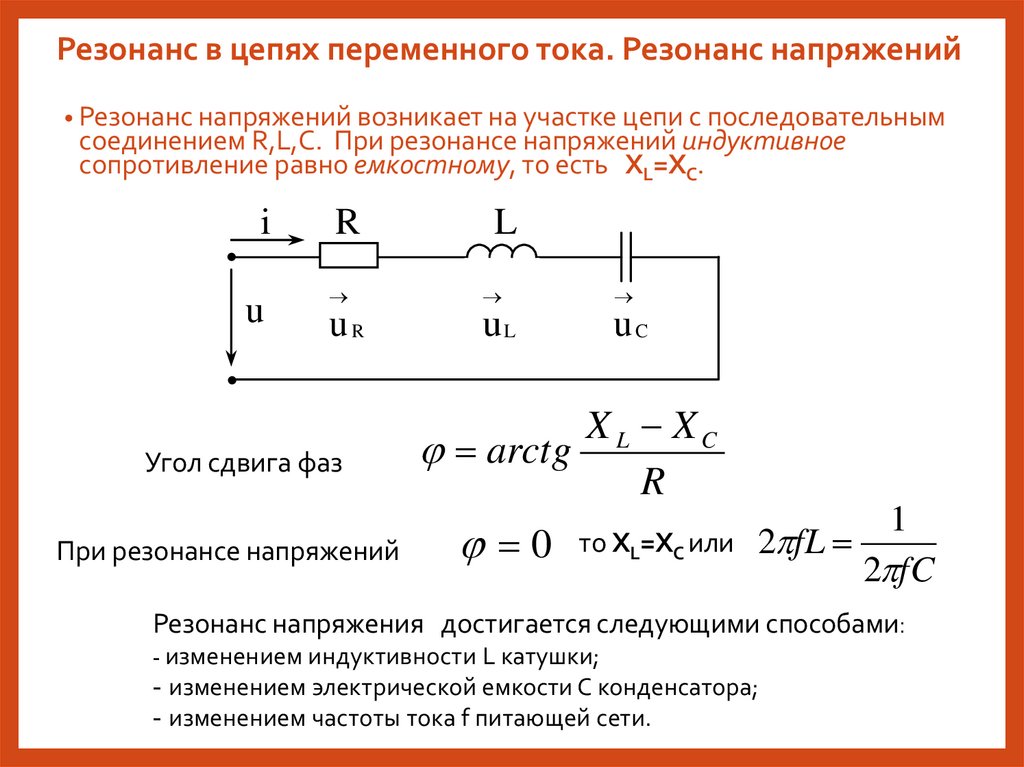
Резонанс в цепях переменного тока. Резонанс напряжений• Резонанс напряжений возникает на участке цепи с последовательным
соединением R,L,C. При резонансе напряжений индуктивное
сопротивление равно емкостному, то есть XL=XC.
i
u
R
L
uR
uL
uC
Угол сдвига фаз
При резонансе напряжений
X L XC
arctg
R
1
0 то XL=XC или 2 fL
2 fC
Резонанс напряжения достигается следующими способами:
- изменением индуктивности L катушки;
- изменением электрической емкости С конденсатора;
- изменением частоты тока f питающей сети.
27.
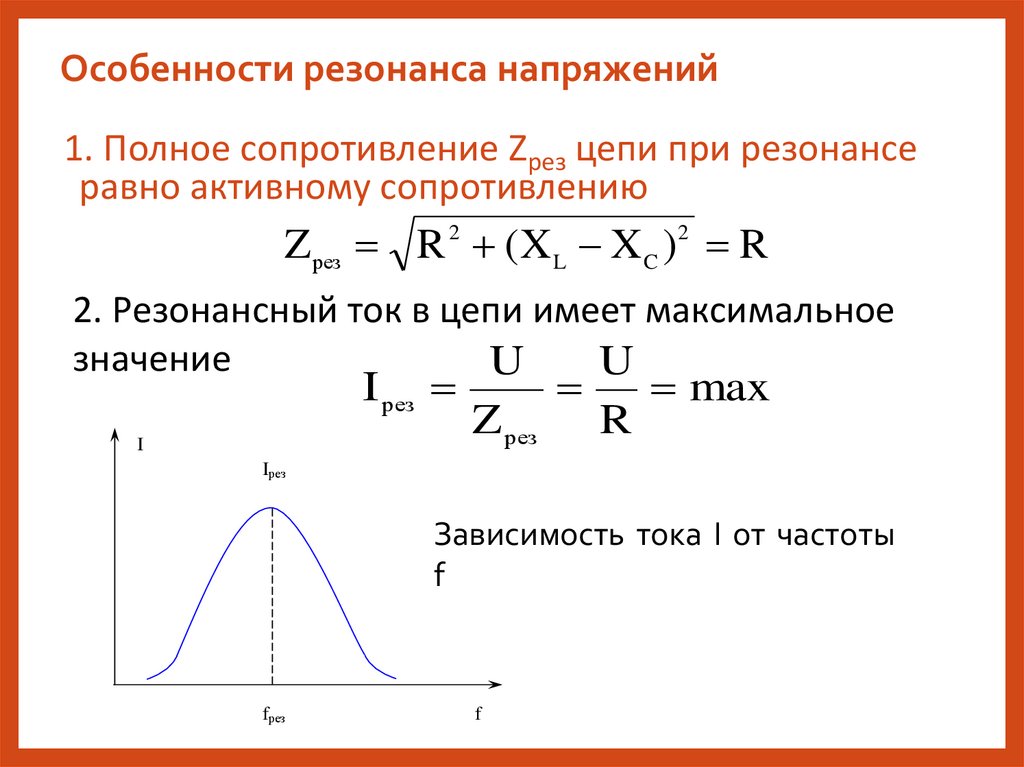
Особенности резонанса напряжений1. Полное сопротивление Zрез цепи при резонансе
равно активному сопротивлению
Z рез R 2 ( X L X C )2 R
2. Резонансный ток в цепи имеет максимальное
значение
U
U
I рез
I
Z рез
R
max
Iрез
Зависимость тока I от частоты
f
fрез
f
28.
3. Напряжение на участке с активным сопротивлением Rравно напряжению питания U и совпадает с ним по фазе.
U UR
4. Активная мощность при резонансе имеет максимальное значение
P RI рез max
2
Если X L X C , > R тогда
UL UC > UR U
То есть напряжения на участках с реактивными элементами
(UL и UC) будут больше напряжения питания U. Свойство
усиления напряжения используется широко используются в
радиоэлектронных устройствах и в заводских промышленных
установках.
29.
,Коэффициент усиления напряжения
равен добротности контура
UL
Q
.
U
Векторная диаграмма при резонансе
напряжений
=0,
U С U L , U R U
30.
Резонанс токов Индуктивная проводимостьЕмкостная проводимость
Угол сдвига фаз
31.
;;.
Характерные особенности
резонанса токов
;
.
YЭ (G1 G2 ) 2 ( BL BC ) 2 G1 G2 GЭ
I UGЭ min .
I1a G1U
I 2a G2U
I1p BLU
I 2p BCU
Токи в первой и второй ветвях
32.
Ток в общей части цепи равен активнойсоставляющей тока





















 Физика
Физика








