Похожие презентации:
Таблица производных
1.
ТАБЛИЦА ПРОИЗВОДНЫХC R, C const
r '
r R
x
C
'
sin x
'
e
x '
a
x '
cos x
a 0, a 1
'
tgx
x n, n Z
2
ctgx '
x n, n Z
ln x
x 0
log a x
x 0, a 0, a 1
'
'
'
'
x
x 0
1
x
arcsin x '
x 1
arccos x '
'
arctgx
'
arcctgx
'
x 0
x 1
2.
==
kсек x 0 k кас
vср
=
=
f
'
x
f
x 0
x
x 0
11)Производная функции
f ' x
y=f(x) в точке x –
12)Физический
смысл(Ньютон):
13)Геометрический смысл
(Лейбниц):
v м гн
14)Функция, имеющая производную в точке x , называется ……..
15)Нахождение производной функции – ………………….
16)П Р А В И Л А Д И Ф Ф Е Р Е Н Ц И Р О В А Н И Я
'
'
1. u v
2. C u
u
4.
v
3. u v
5. f x
'
'
'
3.
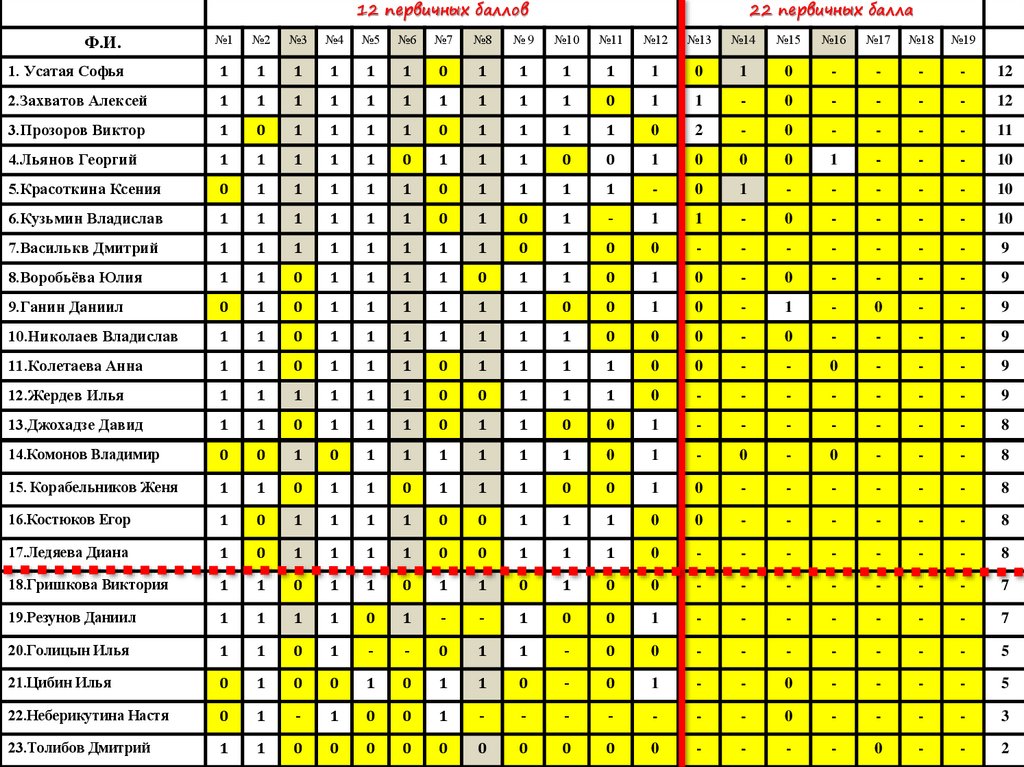
12 первичных баллов22 первичных балла
Ф.И.
№1
№2
№3
№4
№5
№6
№7
№8
№9
№10
№11
№12
№13
№14
№15
№16
№17
№18
№19
1. Усатая Софья
1
1
1
1
1
1
0
1
1
1
1
1
0
1
0
-
-
-
-
12
2.Захватов Алексей
1
1
1
1
1
1
1
1
1
1
0
1
1
-
0
-
-
-
-
12
3.Прозоров Виктор
1
0
1
1
1
1
0
1
1
1
1
0
2
-
0
-
-
-
-
11
4.Льянов Георгий
1
1
1
1
1
0
1
1
1
0
0
1
0
0
0
1
-
-
-
10
5.Красоткина Ксения
0
1
1
1
1
1
0
1
1
1
1
-
0
1
-
-
-
-
-
10
6.Кузьмин Владислав
1
1
1
1
1
1
0
1
0
1
-
1
1
-
0
-
-
-
-
10
7.Василькв Дмитрий
1
1
1
1
1
1
1
1
0
1
0
0
-
-
-
-
-
-
-
9
8.Воробьёва Юлия
1
1
0
1
1
1
1
0
1
1
0
1
0
-
0
-
-
-
-
9
9.Ганин Даниил
0
1
0
1
1
1
1
1
1
0
0
1
0
-
1
-
0
-
-
9
10.Николаев Владислав
1
1
0
1
1
1
1
1
1
1
0
0
0
-
0
-
-
-
-
9
11.Колетаева Анна
1
1
0
1
1
1
0
1
1
1
1
0
0
-
-
0
-
-
-
9
12.Жердев Илья
1
1
1
1
1
1
0
0
1
1
1
0
-
-
-
-
-
-
-
9
13.Джохадзе Давид
1
1
0
1
1
1
0
1
1
0
0
1
-
-
-
-
-
-
-
8
14.Комонов Владимир
0
0
1
0
1
1
1
1
1
1
0
1
-
0
-
0
-
-
-
8
15. Корабельников Женя
1
1
0
1
1
0
1
1
1
0
0
1
0
-
-
-
-
-
-
8
16.Костюков Егор
1
0
1
1
1
1
0
0
1
1
1
0
0
-
-
-
-
-
-
8
17.Ледяева Диана
1
0
1
1
1
1
0
0
1
1
1
0
-
-
-
-
-
-
-
8
18.Гришкова Виктория
1
1
0
1
1
0
1
1
0
1
0
0
-
-
-
-
-
-
-
7
19.Резунов Даниил
1
1
1
1
0
1
-
-
1
0
0
1
-
-
-
-
-
-
-
7
20.Голицын Илья
1
1
0
1
-
-
0
1
1
-
0
0
-
-
-
-
-
-
-
5
21.Цибин Илья
0
1
0
0
1
0
1
1
0
-
0
1
-
-
0
-
-
-
-
5
22.Неберикутина Настя
0
1
-
1
0
0
1
-
-
-
-
-
-
-
0
-
-
-
-
3
23.Толибов Дмитрий
1
1
0
0
0
0
0
0
0
0
0
0
-
-
-
-
0
-
-
2
4.
3A
A
Г
Планиметрия. Углы и длины
Планиметрия. Площади
2
Простейшие уравнения
Графики и диаграммы
1
Теория вероятностей
Арифметические задачи
№
5
6
A
A
Г
К К К К
№1
У У У У
№2
Р Р Р Р
РТ
С С С С
ЫЫЫ Ы
К К №
К
11
У У Р У
Р Р Т Р
С С
С
ЫЫ
Ы
СР
С
6 2 Р 1
4 7 3 5
Геометрический смысл
производной
СТЕРЕОМЕТРИЯ
Значение выражения
Задачи прикладного характера
Задачи на составление уравнений
Исследование функции
Уравнения
Стереометрия
Неравенства
Планиметрия
Экономика
Параметр
Численные задачи
4
A
Г
А
А
А
А
А
Г
А
Г
А
А
А
7
8
9
10 11 12 13 14 15 16 17 18 19
5.
Выпуклость графиков функцийГрафик функции называется выпуклым вниз (#
)
на (a ; b), если касательная, проведённая в ∀ его
точке (a ; b), лежит ниже графика функции.
x
tg
f x
'
f x
f x 0
''
f x
y
y
y f x
1
a
2
3
x1 x2 x3 b x
y f x
a x1 x2
1
x3
2
3
b
x
6.
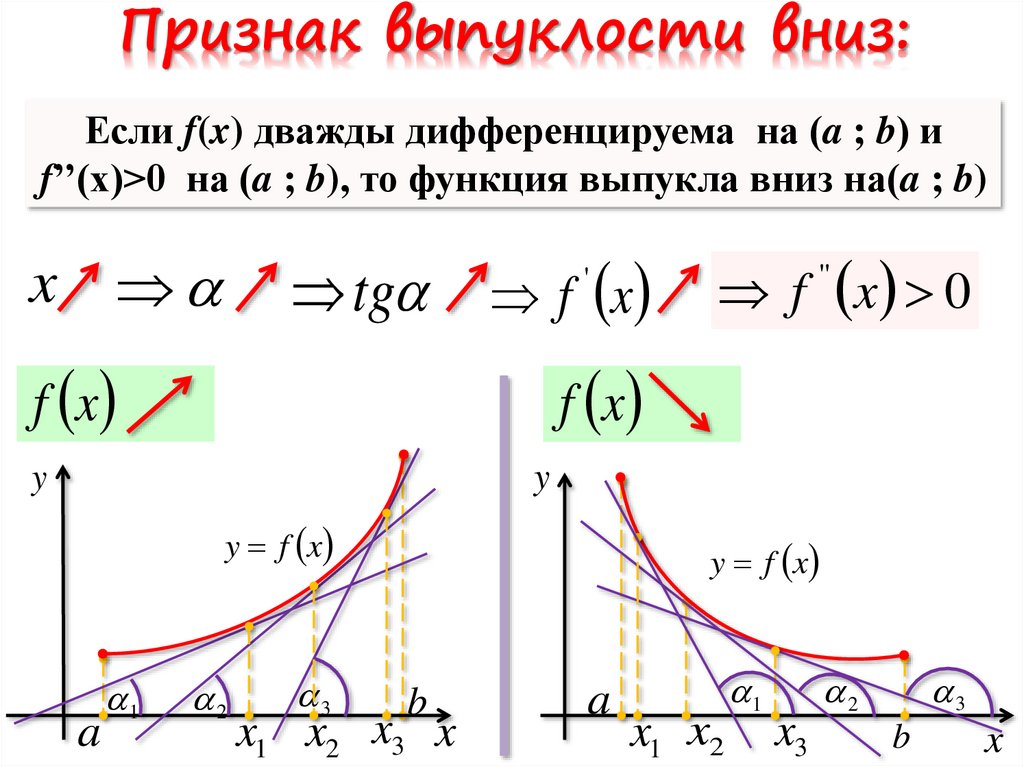
Признак выпуклости вниз:Если f(x) дважды дифференцируема на (a ; b) и
f’’(x)>0 на (a ; b), то функция выпукла вниз на(a ; b)
x
tg
f x
'
f x
f x 0
''
f x
y
y
y f x
a
1
2
3
y f x
b
x1 x2 x3 x
a
x1 x2
1
x3
2
3
b
x
7.
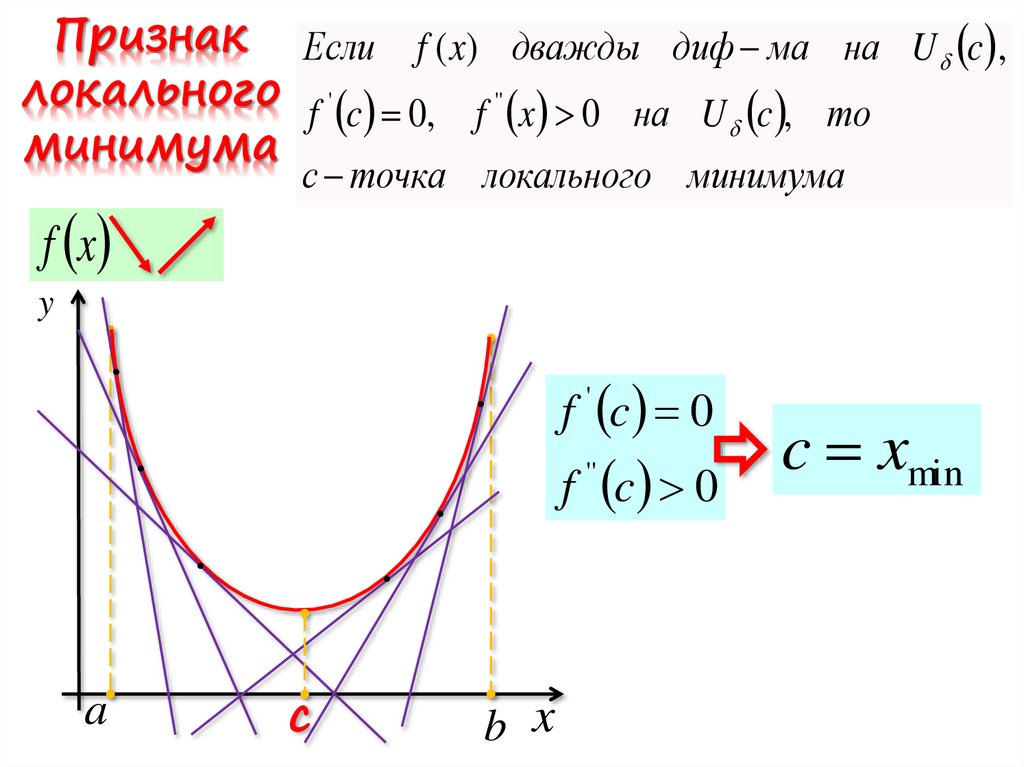
Признак Если f ( x) дважды диф ма на U c ,локального f ' c 0, f '' x 0 на U c , то
минимума
с точка локального минимума
f x
y
f c 0
''
a
f ' c 0
c
b x
c xmin
8.
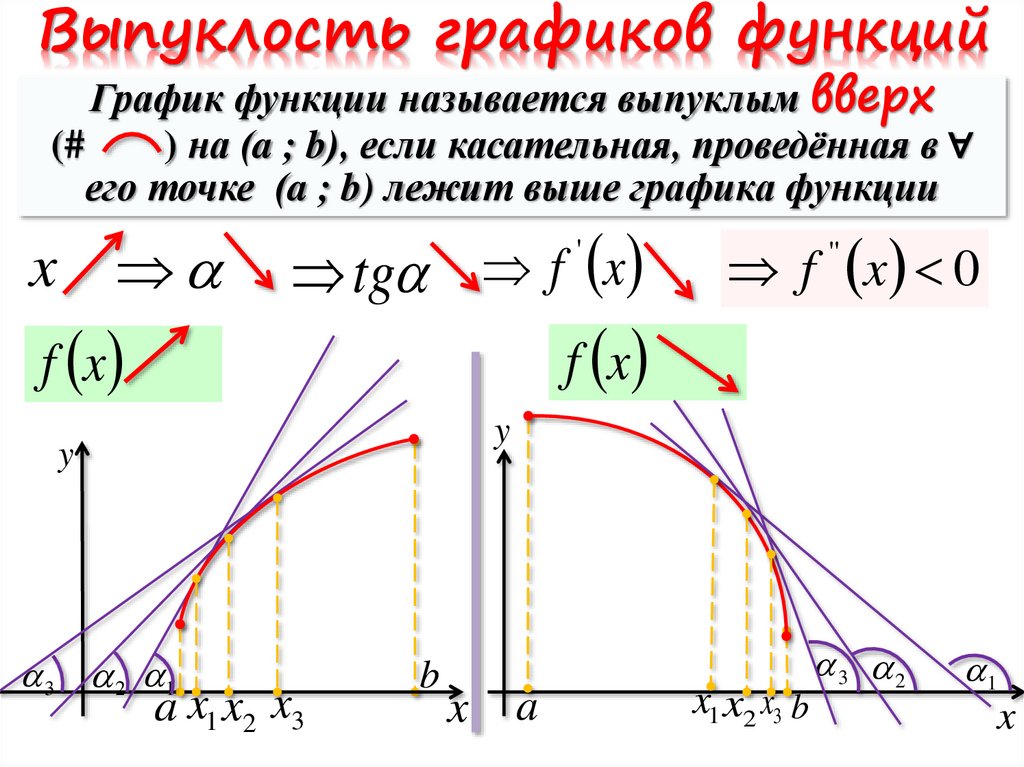
Выпуклость графиков функцийГрафик функции называется выпуклым вверх
(#
) на (a ; b), если касательная, проведённая в ∀
его точке (a ; b) лежит выше графика функции
x
tg f x
'
f x 0
''
f x
f x
y
y
3 2 1
a x1 x2 x3
b
x
a
x1 x2 x3 b
3 2
1
x
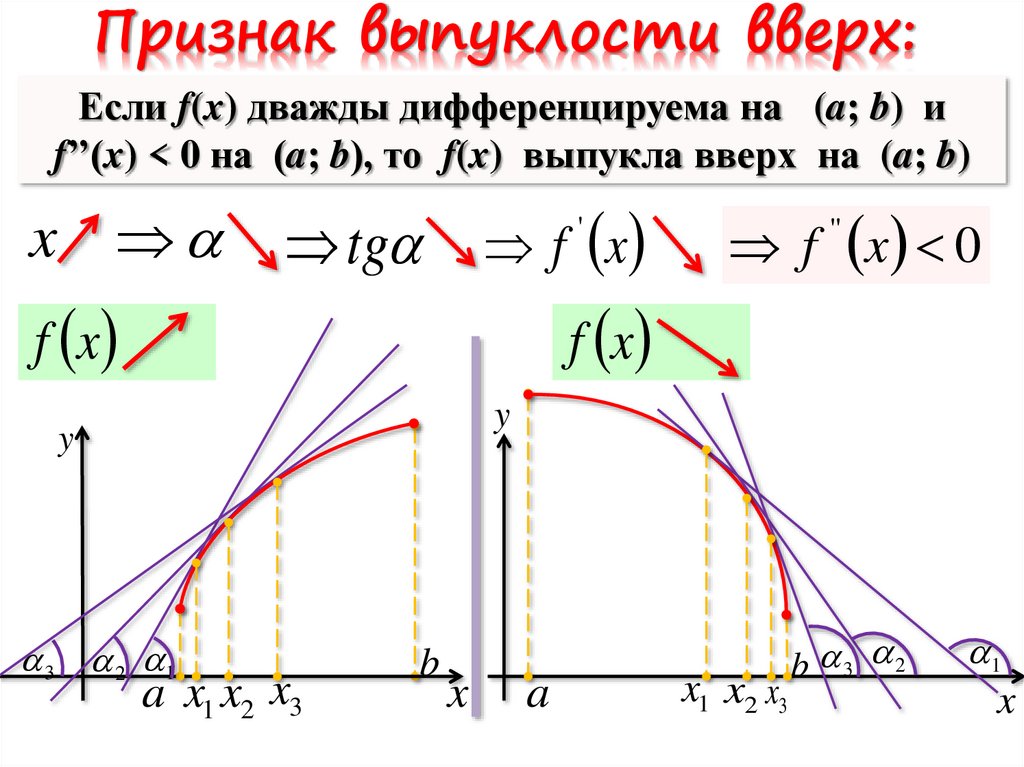
9.
Признак выпуклости вверх:Если f(x) дважды дифференцируема на (a; b) и
f’’(x) < 0 на (a; b), то f(x) выпукла вверх на (a; b)
x
f x
tg
'
f x
f x 0
''
f x
y
y
3 2 1
a x1 x2 x3
b
x
a
x1 x2 x3
b 3 2
1
x
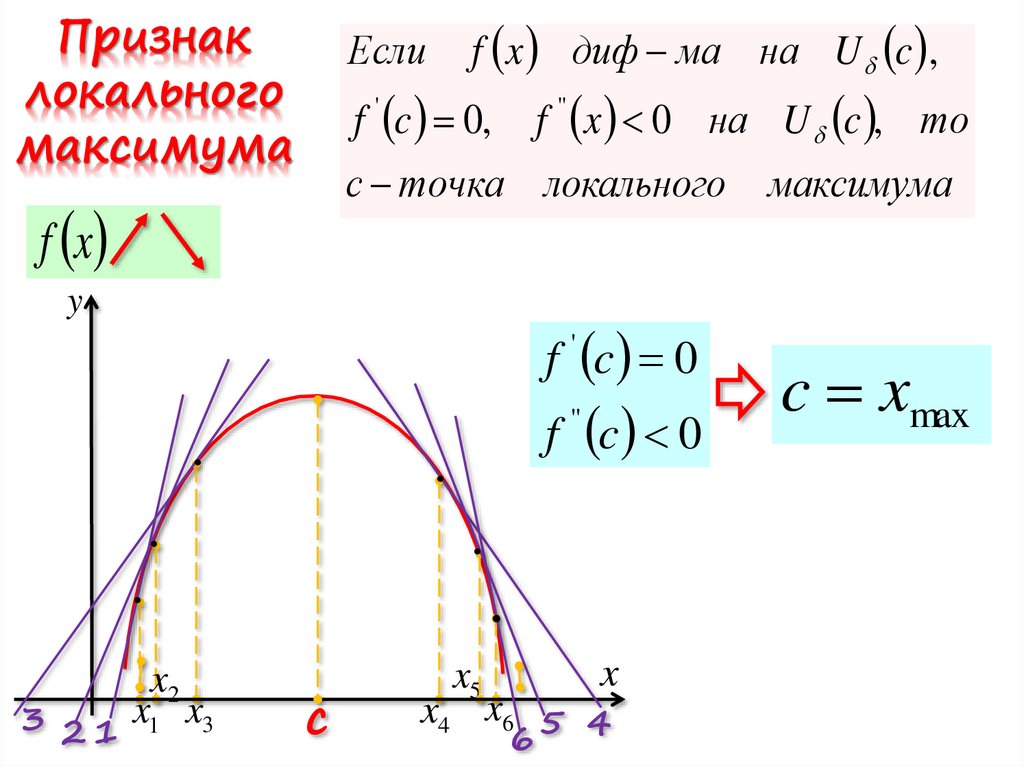
10.
Признаклокального
максимума
f x диф ма на U c ,
Если
f ' c 0,
f '' x 0 на U c , то
с точка локального
f x
y
f ' c 0
f c 0
''
x2
3 2 1 x1 x3
c
x5
x
x4 x6 5 4
6
максимума
c xmax
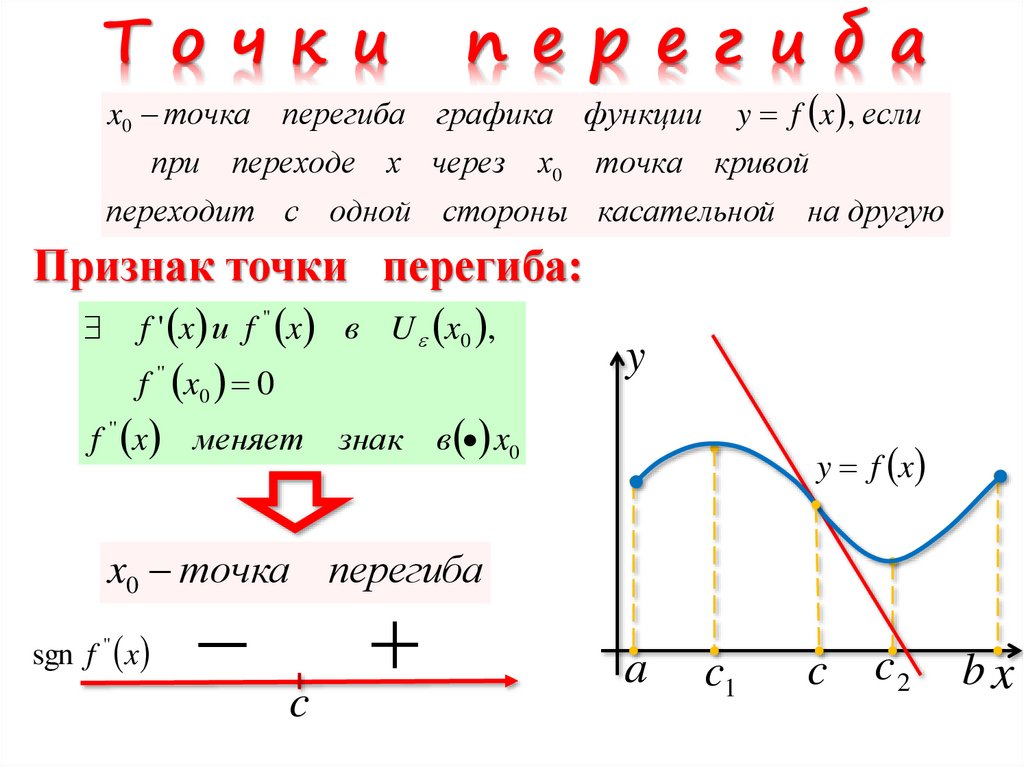
11.
Т о ч киперегиба
x0 точка перегиба графика функции
при переходе х через
х0
y f x , если
точка кривой
переходит с одной стороны касательной на другую
Признак точки перегиба:
f ' x и f " x в U x0 ,
y
''
f x0 0
f '' x меняет знак в x0
y f x
x0 точка перегиба
sgn f '' x
c
a
c1
c
c2
bx
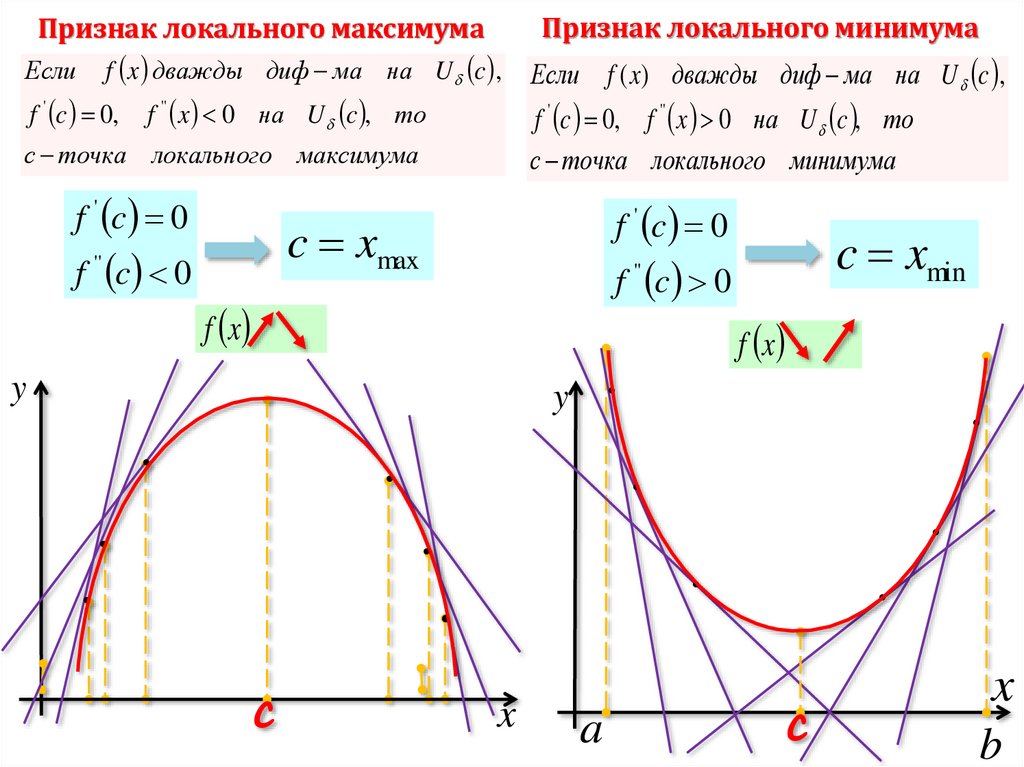
12.
Признак локального максимумаПризнак локального минимума
Если
Если f ( x) дважды диф ма на U c ,
f x дважды диф ма на U c ,
f ' c 0,
f '' x 0 на U c , то
f ' c 0, f '' x 0 на U c , то
с точка локального минимума
с точка локального максимума
f ' c 0
f c 0
f ' c 0
c xmax
''
c xmin
f c 0
''
f x
f x
y
y
c
x
a
c
x
b







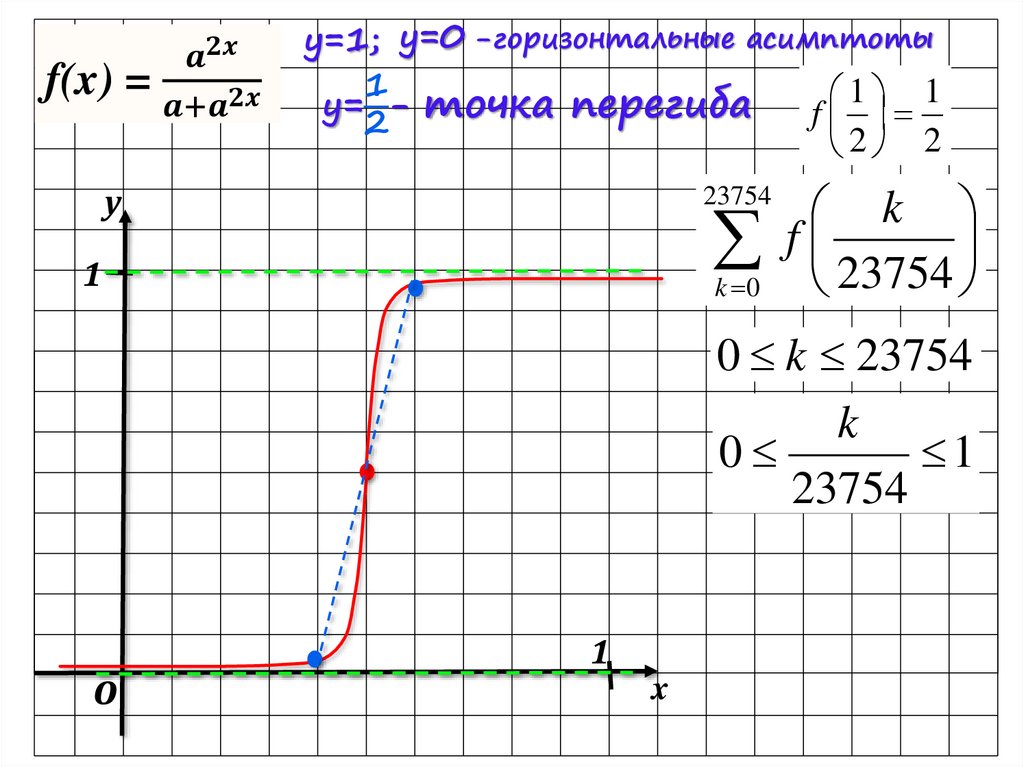
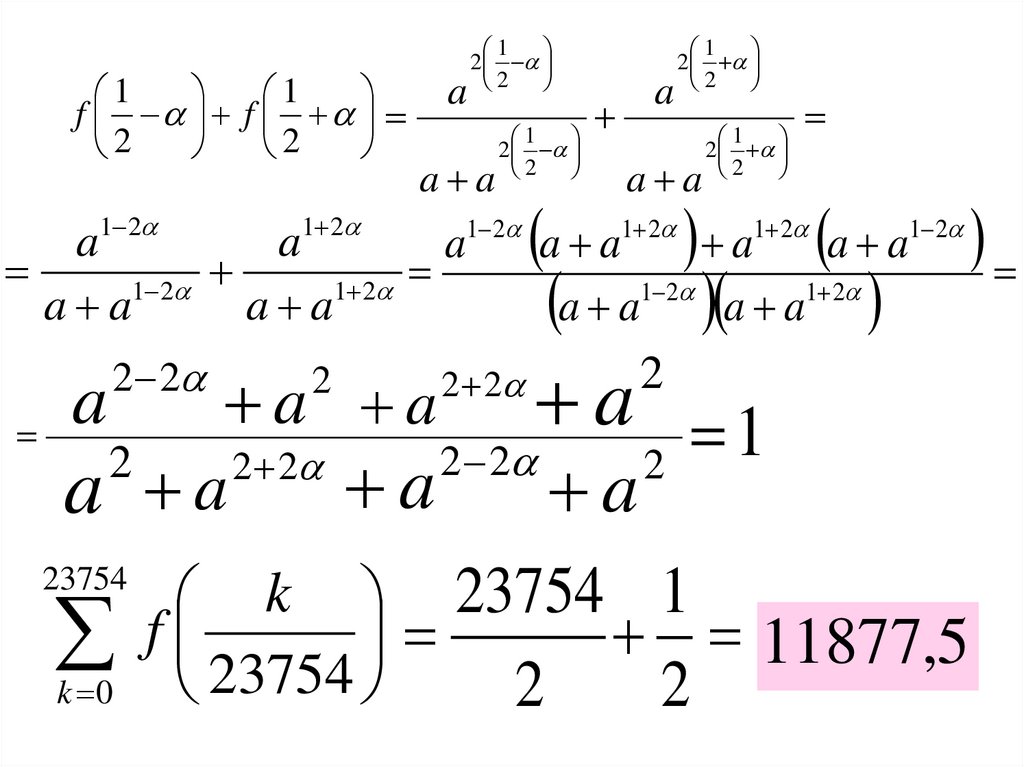
 Математика
Математика








