Производная. Понятие касательной

1.

МБОУ СОШ № 37
Туренко Екатерина
Леонидовна
г. Хабаровск

2.

Понятие касательной
Задача о касательной
Задача о скорости движения
Общее определение производной
Смысл производной
Зависимость между непрерывностью и дифференцируемостью функции
Основные правила Дифференцирования функций
Производная сложной функции
Производная обратной функции
Производная неявной функции
Производная функции, заданной параметрически
Понятие о производных высших порядков
Теорема о конечном приращении функции и ее следствия
Теорема Ролля
Теорема Ферма
Возрастание и убывание функции одной переменной
Экстремум функции одной переменной
Вогнутость и выпуклость графика функции. Точки перегиба

3.

Понятие касательной
Определение: Касательной к данной непрерывной кривой в
данной ее точке М (точка касания)
называется предельное положение секущей
ММ', проходящей через точку М, когда
вторая точка пересечения М' неограниченно
приближается по кривой к первой.
Рис. 1

4.

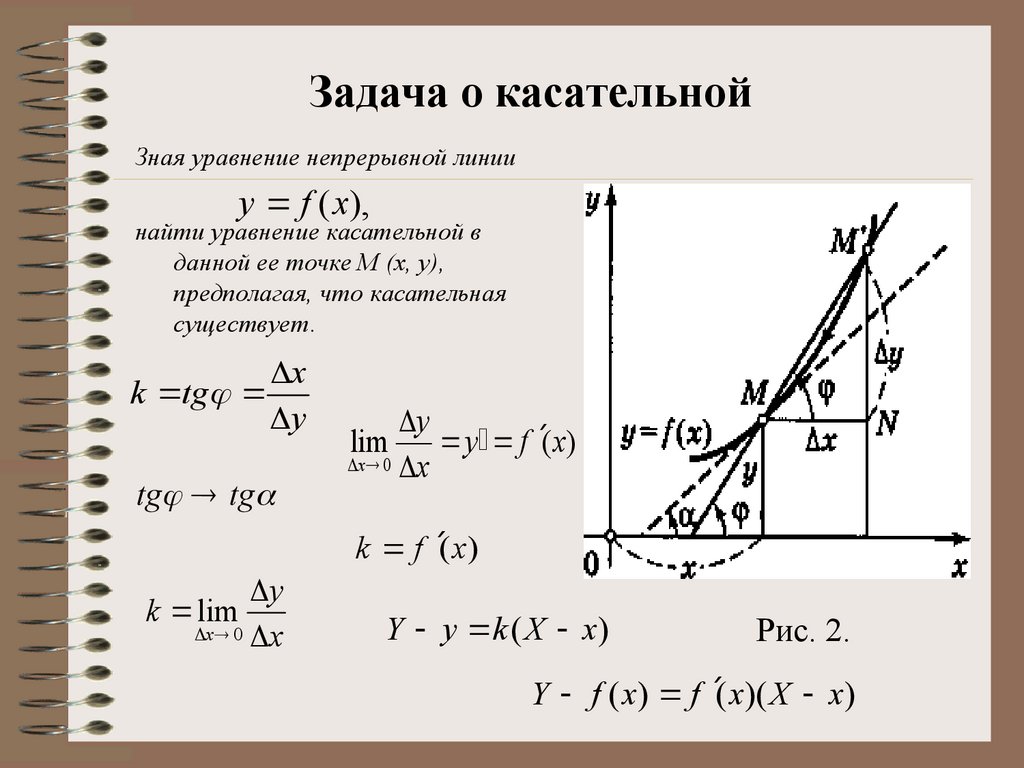
Задача о касательной
Зная уравнение непрерывной линии
y f (x),
найти уравнение касательной в
данной ее точке М (х, у),
предполагая, что касательная
существует.
k tg
x
y
tg tg
y
lim
y f ( x)
x 0 x
k f (x)
y
k lim
x 0 x
Y y k ( X x )
Рис. 2.
Y f ( x) f ( x)( X x)

5. Задача о скорости движения

Задача. Зная закон движения S=f(t), найти скорость движущейся
точки для любого момента времени.
ОМ = х
t t
OM x x
x x f t
x f (t t ) f (t )
x f (t t ) f (t )
y
t
V lim
t 0
y
t
v f (t )

6.

Общее определение производной
Определение: Производной функции у = f(х)
называется предел отношения
приращения функции к
приращению аргумента при
условии, что приращение
аргумента стремится к нулю,
если этот предел существует
y
x 0 x
y f ( x) lim
Найти производную функции у = х2
x 0
y = (х + x )2
y
y lim
lim
(2 x x) 2 x
x 0
x 0
x
y ( x x) 2 x 2 2 x * x ( x) 2
(х2)' = 2х

7.

Смысл производной
Физический
Геометрический
Если функция описывает f ( x) k касательной к
какой-либо физический
графику функции y=f (x) в
процесс, то y f (x) есть точке, абсцисса которой
скорость
протекания
равна x.
y
этого процесса.
Например
Точка движется
прямолинейно по закону S t 2
.Найти скорость
движения в момент
времени
t=3
y=kx+b
Уравнение
касательной к кривой
y x 2 1
в точке А(1;2)
k y ( x) ( x 2 1) 2 x
k=2*1=2
2=2*1+b
b=0
y=2x

8.

Зависимость между непрерывностью
и дифференцируемостью функции
Мы видели, что функция
y f (x)
называется непрерывной в точке х, если в этой
точке
lim
y 0
x 0
Функция называется дифференцируемой в
точке х, если в этой точке она имеет производную,
т. е. если существует конечный предел:
lim
x 0
y
y
x

9.

Зависимость между
непрерывностью и
дифференцируемостью функции
ТЕОРЕМА:
Если функция дифференцируема
в некоторой точке, то в этой
точке функция непрерывна.
Обратное утверждение неверно:
непрерывная функция может не
иметь производной.

10.

Основные правила
дифференцирования функций:
I. Производная постоянной величины равна нулю.
II. Производная алгебраической суммы конечного числа
дифференцируемых функций равна такой же алгебраической
сумме производных этих функций.
III. Производная произведения двух дифференцируемых
функций равна произведению первого сомножителя на производную
второго плюс произведение второго сомножителя на производную
первого.
IV. Производная частного. Если числитель и знаменатель
дроби — дифференцируемые функции и знаменатель не обра
щается в нуль, то производная дроби равна также дроби,
числитель которой есть разность произведений знаменателя
дроби на производную числителя и числителя дроби на
производную знаменателя, а знаменатель есть квадрат
прежнего знаменателя.

11.

Производная сложной функции
ТЕОРЕМА:
Если у = f(z)и z= (x)— дифференцируемые
функции от своих аргументов, то производная
сложной функции
y f (x)
существует и равна производной данной
функции у по промежуточному аргументу z,
умноженной на производную самого промежуточного
аргумента г по независимой переменной х, т. е.
y x y z z x
Например
2
y ln( x 3x 1)
1
y x y * x (2 x 3)
u
y ln
x 2 3x 1
2x 3
x 2 3x 1

12.

Производная обратной функции
ТЕОРЕМА. Для дифференцируемой функции с
производной, не равной нулю, производная обратной
функции равна обратной величине производной данной
функции.
Доказательство. Пусть у = f(х) Например y=arctg x
y 0
x=tg x обратная для y
y x f ( x) 0
1
1
x ( y )
x
y x
1
(tgy )
cos 2 x
x
y
2
1 :
cos
y
cos 2 y
y
x
cos 2 y sin 2 y
1
x
y
2
lim
1 : lim
cos
y
y 0 y
x 0 x
2
1
2
1
ctg
y
sin y
1
1
1
xy
2
1
tg
x
yx
1 x2

13.

Производная неявной функции
Определение:
Если y как функция от x задается
соотношением F(x, y)=0, где F(x, y) выражение, содержащее x и y, то y
называется неявной функции от x.
Алгоритм нахождения производных заданных
функций в неявном виде.
1) Находим производную от
y
Пример.
Найти
левой части равенства F(x,
y)=0, рассматривая y как
x 3 y 2 5 xy 4
функцию от x и
3 2
приравниваем ее к нулю.
(5 xy ) 4
(
x
y
)
2) Решаем полученное уравнение
относительно y, в
( x 3 ) y 2 x 3 ( y 2 ) (5 x) y 5 xy 0
результате будем иметь
выражение производной от
2 2
3
неявной функции в виде
3x y x 2 yy 5 y 5 xy
y=f(x)

14.

Производная функции, заданной
параметрически
ТЕОРЕМА:
Если
функция
параметрически
у
от
x (t )
где функции (t ) и
и
t 3
y (t )
yt
xt
Например
yt 3t 2
xt 2t
3
y x yt : xt 3t : 2t t
2
задана
(t ) 0 , то производная
y
этой функции есть
x
t 2
х
(t )
дифференцируемы и
x
y
аргумента
2

15.

Понятие о производных высших порядков
Производная f '(х) от
Пример
функции f (х) называется
производной первого порядка
1)Пусть y = sin x
и представляет собой
Тогда имеем последовательно
некоторую новую функцию.
y cos x, y sin x, y cos x, y IV sin x,.....
Может случиться, что эта
3
функция сама имеет
2)Пусть y ( x) 4 x 2 cos x
производную. Тогда
Найти: y
производная от производной
2
y
12
x
2 sin x
первого порядка называется
производной второго порядка
y 24 x 2 cos x
или второй производной и
y 24 x 2 sin x
обозначается так: f "(х).
Итак,
f ( x) f ( x)
f ( x) f ( x)

16.

Теорема о конечном приращении
функции и ее следствия
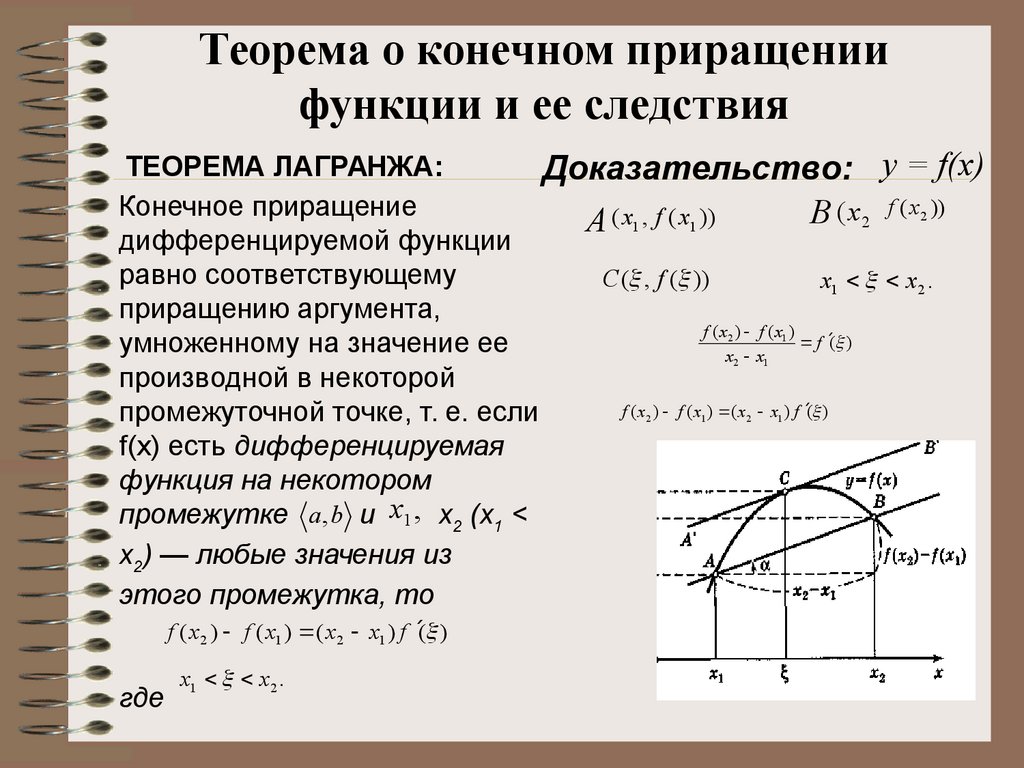
ТЕОРЕМА ЛАГРАНЖА:
Доказательство: у = f(х)
Конечное приращение
B (x 2 f ( x2 ))
A ( x1 , f ( x1 ))
дифференцируемой функции
равно соответствующему
C ( , f ( ))
x1 x 2 .
приращению аргумента,
f (x ) f (x )
f ( )
умноженному на значение ее
x x
производной в некоторой
f ( x ) f ( x ) ( x x ) f ( )
промежуточной точке, т. е. если
f(х) есть дифференцируемая
функция на некотором
промежутке a, b и x1 , х2 (х1 <
х2) — любые значения из
этого промежутка, то
2
1
2
2
f ( x 2 ) f ( x1 ) ( x 2 x1 ) f ( )
где
x1 x 2 .
1
1
2
1

17.

ТЕОРЕМА РОЛЛЯ:
Между двумя последовательными корнями
дифференцируемой функции всегда содержится, по
меньшей мере, один корень ее производной.
Доказательство: В самом деле, если f(х) —
дифференцируемая функция и
то из формулы имеем
f ( x1 ) f ( x 2 ) 0( x1 x 2 )
( x 2 x1 ) f ( ) 0
или, так как , x 2 x1
f ( ) 0, где x1 x 2

18.

ТЕОРЕМА ФЕРМА:
Если функция y=f (х) определена и непрерывна (a,
x0
b) и пусть эта функция принимает max во внутренней
f ( x0 ) 0
f ( x0 ),
точке
этого интервала, тогда если существует
то
y f (x)
x0
x0 a, b
x (a, b) функция
Доказательство: Пусть в точке
f ( xлюбых
a, b f ( x) для
x значение
0 ), x x0
принимает max
,
для любых,
f ( x) f ( x0 ) 0,
x x0
следовательно
для любых f ( x) f ( x0 )
f ( x0 ) lim
x x0
Существует функция
f ( x0 ) lim
x x 0
f ( x0 ) lim
x x0 0
f ( x ) f ( x0 )
0,
x x0
f ( x) f ( x0 )
0,
x x0
x x0
f ( x ) 0
т.е.
f ( x0 ) 0
f ( x) 0
Следовательно,

19.

Возрастание и убывание
функции одной переменной
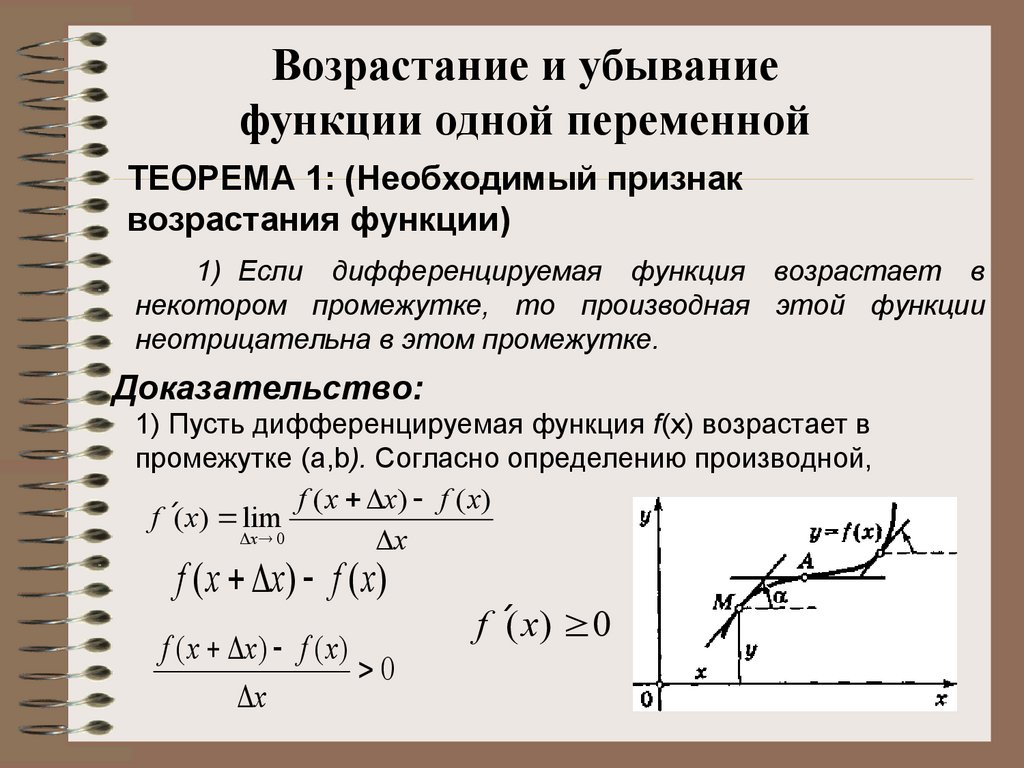
ТЕОРЕМА 1: (Необходимый признак
возрастания функции)
1) Если дифференцируемая функция возрастает в
некотором промежутке, то производная этой функции
неотрицательна в этом промежутке.
Доказательство:
1) Пусть дифференцируемая функция f(х) возрастает в
промежутке (a,b). Согласно определению производной,
f ( x x) f ( x)
f ( x) lim
x 0
x
f ( x x) f ( x)
f ( x x) f ( x)
0
x
f ( x) 0

20.

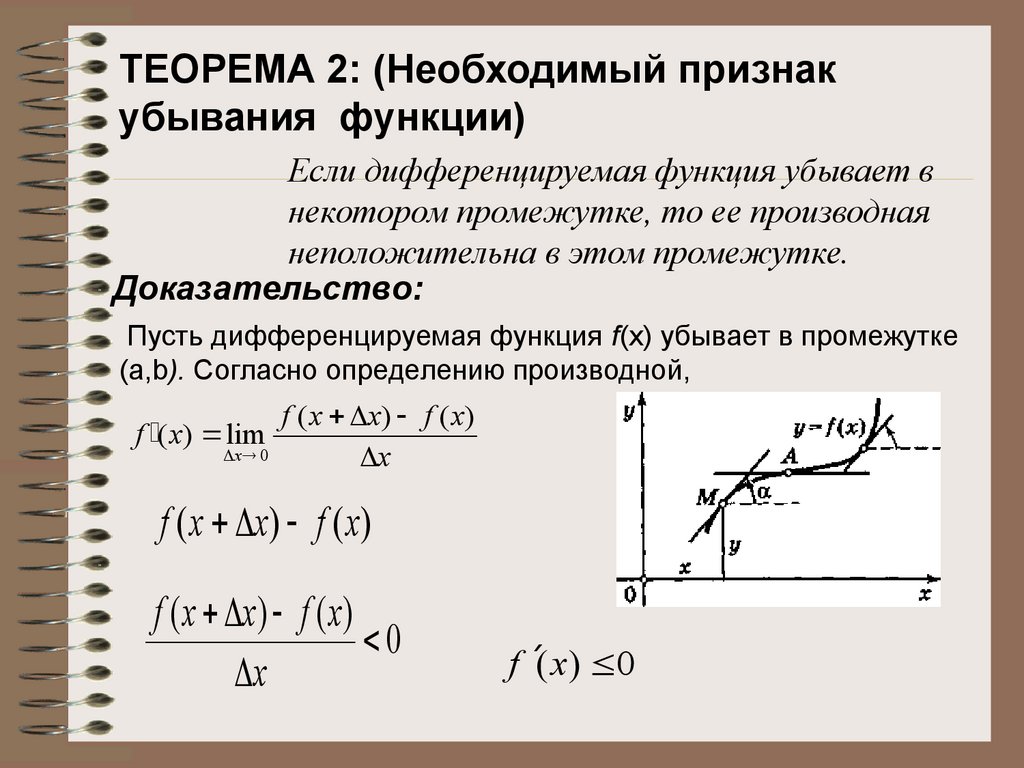
ТЕОРЕМА 2: (Необходимый признак
убывания функции)
Если дифференцируемая функция убывает в
некотором промежутке, то ее производная
неположительна в этом промежутке.
Доказательство:
Пусть дифференцируемая функция f(х) убывает в промежутке
(a,b). Согласно определению производной,
f ( x) lim
x 0
f ( x x) f ( x)
x
f ( x x) f ( x)
f ( x x) f ( x)
0
x
f ( x) 0

21.

ТЕОРЕМА: Достаточный признак
возрастания функции
1) Если производная дифференцируемой функции
положительна внутри некоторого промежутка, то
функция возрастает на этом промежутке.
Доказательство:
1) Пусть, например, дифференцируемая функция f(х)
f ( x) 0
такова, что
при
a x b
Для любых двух значений a x1 x 2 b
,
принадлежащих промежутку (а, b), в силу теоремы о
конечном приращении функции имеем
f ( x 2 ) f ( x1 ) 0
где
— промежуточное значение между x1 и x 2 и,
следовательно, лежащее внутри промежутка (а, b).
Так как x 2 x1 0
и f ( x 2 ) f ( x1 ) 0
то отсюда
получим
f ( ) 0
Следовательно, функция f(x) возрастет на промежутке
(а, b).

22.

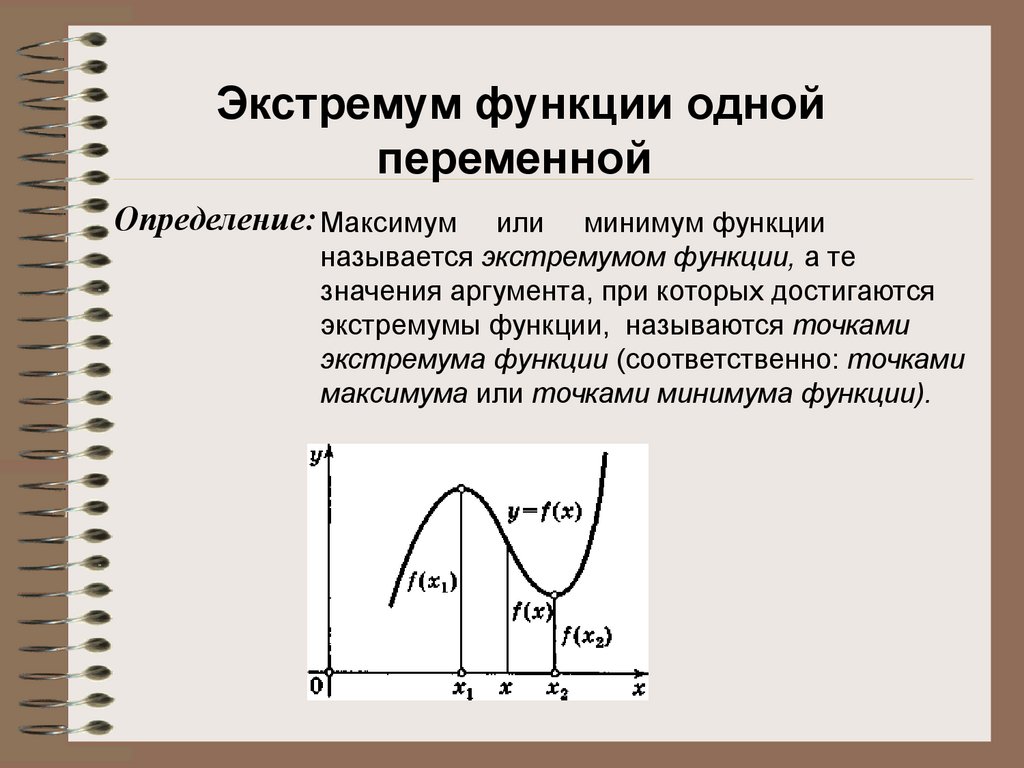
Экстремум функции одной
переменной
Определение: Максимум
или минимум функции
называется экстремумом функции, а те
значения аргумента, при которых достигаются
экстремумы функции, называются точками
экстремума функции (соответственно: точками
максимума или точками минимума функции).

23.

НЕОБХОДИМОЕ УСЛОВИЕ
ЭКСТРЕМУМА ФУНКЦИИ
ТЕОРЕМА. В точке экстремума (двустороннего)
дифференцируемой функции производная ее равна нулю.
Доказательство. Пусть, для определенности, x0 есть
точка минимума функции f(x).
f ( x0 x0 ) f ( x0 )
f ( x 0 x) f ( x0 )
0
x0
f ( x0 x) f ( x0 )
0
x0
f ( x 0 x )
f ( x0 ) lim
x 0
x0
f ( x0 ) 0,
x0 0
f ( x0 ) 0
x0 0
f ( x 0 ) 0

24.

ДОСТАТОЧНЫЕ УСЛОВИЯ
ЭКСТРЕМУМА ФУНКЦИИ
ТЕОРЕМА: Если дифференцируемая функция f(х)
такова, что для некоторого значения x0 ее аргумента х
производная f '(х) равна нулю и меняет свой знак при
переходе через это значение, то число является
экстремумом функции f(x), причем:
1) функция f(x) имеет максимум при х — x0 ,если
изменение знака производной f '(х) происходит с плюса
на минус;
2) функция f(х) имеет минимум при х = x0 , если
изменение знака производной f '(x) происходит с минуса
на плюс.
Доказательство. Пусть f( x0 ) = 0, f '(х) > 0 при x0- <х< x0
f '(х) < 0 при x0<х< x0+
x
f ( x ) f ( x)
0
x0 , x0 x0 , x0
f ( x0 ) f ( x)
x<
0
x x0

25.

Вогнутость и выпуклость графика
функции. Точки перегиба
Определение: График дифференцируемой функции у =
f(х) называется вогнутым вверх (или
выпуклым вниз) в промежутке (а, b), если
соответствующая часть кривой
y f ( x)( x a, b )
расположена выше касательной,
проведенной в любой ее точке М(х, f(x)).
Аналогично, график дифференцируемой
функции у = f(х) называется выпуклым вверх
(или вогнутым вниз) в промежутке (а, b),
если соответствующая часть кривой
расположена ниже касательной,
проведенной к любой ее точке М(х, f(х))
Определение: Точкой перегиба графика дифференцируемой
функции у = f(х) называется его точка, при
переходе через которую кривая меняет свою
вогнутость на выпуклость или наоборот

26.

ТЕОРЕМА:
Если для дважды дифференцируемой функции y =
f(х) вторая ее производная f "(х) положительна внутри
промежутка (а,b), то график этой функции вогнут
вверх в данном промежутке.
Доказательство:
Пусть f "(х) > 0 при а<х<bих0 — любая
точка промежутка (а, b). Сравним в
точке х ординату у кривой y=f(x)
ординатой у ее касательной MоN,
проведенной в точке

27.

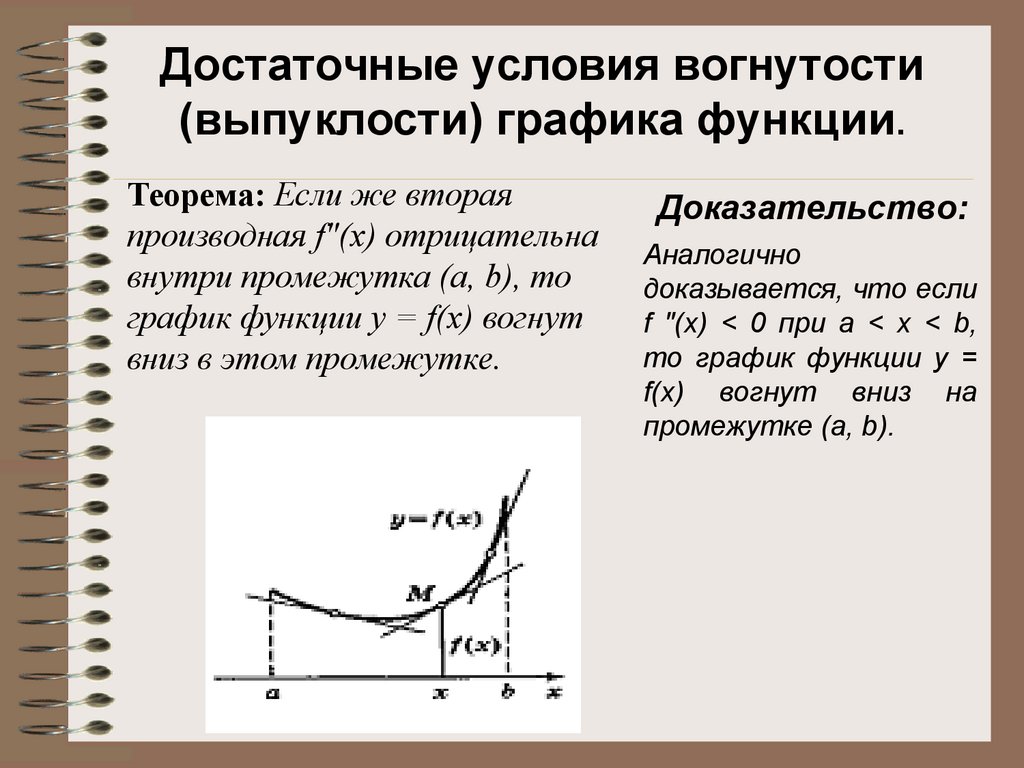
Достаточные условия вогнутости
(выпуклости) графика функции.
Теорема: Если же вторая
производная f"(х) отрицательна
внутри промежутка (а, b), то
график функции у = f(х) вогнут
вниз в этом промежутке.
Доказательство:
Аналогично
доказывается, что если
f "(x) < 0 при а < х < b,
то график функции у =
f(х) вогнут вниз на
промежутке (а, b).