Похожие презентации:
Теорема Пифагора. Самое быстрое доказательство теоремы
1.
2.
№ 1. По данным рисунка найдите площадь АВСВ
10 см
A
S ABC =
ВС =
S ABC =
С
AC BС
АВ = 12 : 2 = 6 см (катет против угла в 30о)
AC BС = (10 6) : 2 = 30 см2
3.
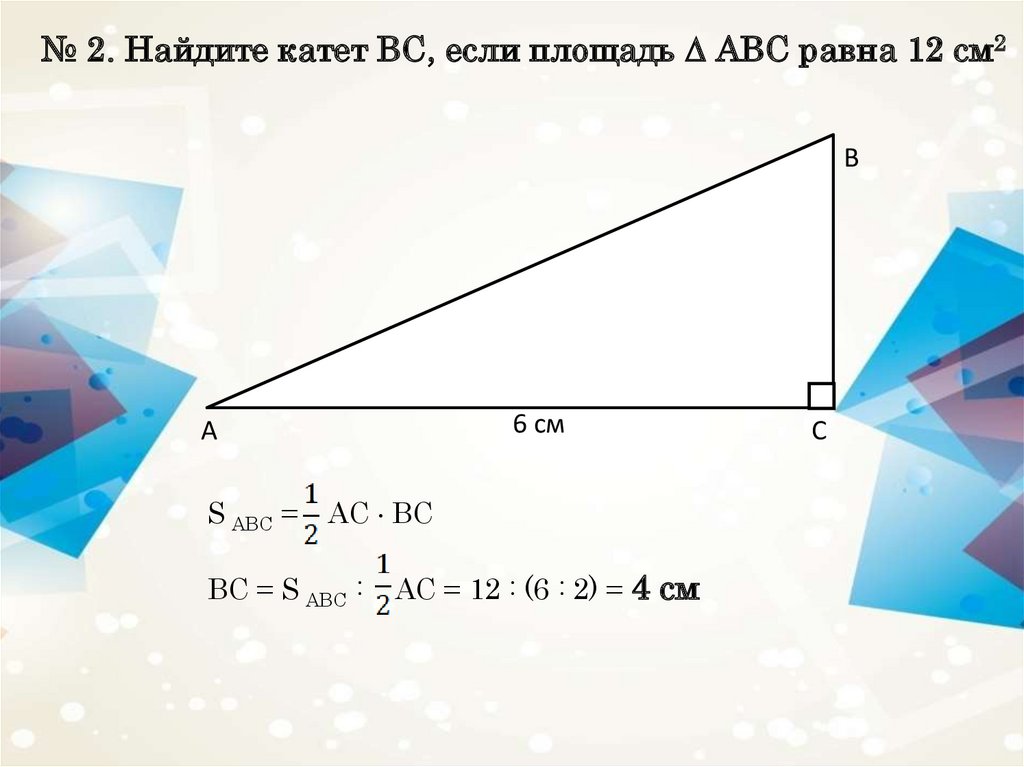
№ 2. Найдите катет ВС, если площадь АВС равна 12 см2В
6 см
A
S ABC =
AC BС
ВС = S ABC :
АС = 12 : (6 : 2) = 4 см
С
4.
№ 3. По данным рисунка найдите площадь АВСВ
3 см
4 см
A
С
S ABC =
р=
(АВ + ВС + АС) = (3 + 4 + 5) : 2 = 6
S ABC =
=
= 6 см2
5.
ТЕОРЕМА: В прямоугольном треугольнике квадратгипотенузы равен сумме квадратов катетов
С
Дано:
АВС
В = 90о
АВ = а
ВС = b
АС = с
Доказать:
с2 = а2 + b2
b
а
A
В
Доказательство:
1) Достроим треугольник до квадрата со стороной а + b
S 1 = (а + b)2
2) S 1 = 4 S ∆ + S 2 = 4
ab + c2 = 2ab + c2
3) S 1 = S 1
(а + b)2 = 2ab + c2
а2 + 2ab + b2 = 2ab + c2
а2 + b2 = c2
чтд
6.
bb
c
а
а
c
b
b
а
7.
Самое быстрое доказательство теоремы8.
№ 483. Найдите гипотенузу прямоугольноготреугольника по данным катетам a и b
С
Дано:
АВС
АВ = 8 см
ВС = 6 см
Найти:
АС
A
В
Решение:
АC2 = АВ2 + ВС2 (теорема Пифагора)
АС =
=
=
Ответ: 10 см
= 10 см
9.
№ 486.Дано:
В
АВСD - прямоугольник
АВ = 5
АС = 13
Найти:
АD
С
D
A
Решение:
1) AD = ВС (противоположные стороны)
2) АC2 = АВ2 + ВС2 (теорема Пифагора)
ВС2 = АC2 АВ2
ВС =
=
=
Ответ: 12
= 12
10.
Домашнеезадание:
п.54,
задание в Яклассе









 Математика
Математика








