Похожие презентации:
Трапеция. Решение задач
1.
Трапеция. Решение задач6 класс
2.
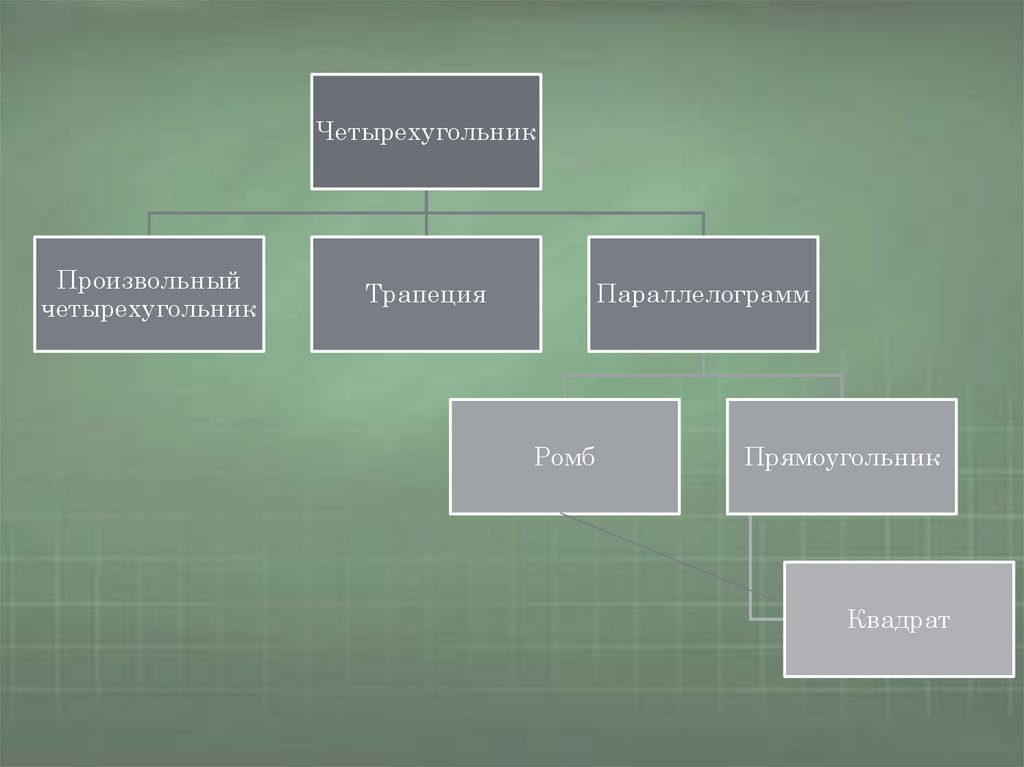
ЧетырехугольникПроизвольный
четырехугольник
Трапеция
Параллелограмм
Ромб
Прямоугольник
Квадрат
3.
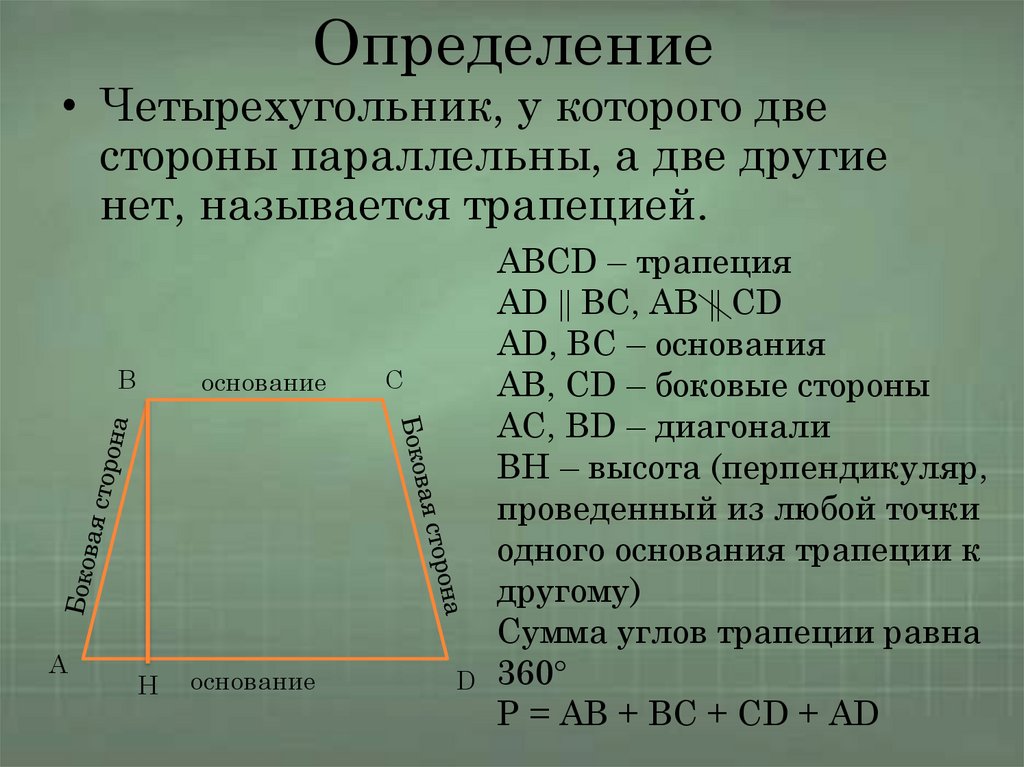
Определение• Четырехугольник, у которого две
стороны параллельны, а две другие
нет, называется трапецией.
B
A
основание
H
основание
C
D
ABCD – трапеция
AD BC, AB CD
AD, BC – основания
AB, CD – боковые стороны
AC, BD – диагонали
BH – высота (перпендикуляр,
проведенный из любой точки
одного основания трапеции к
другому)
Сумма углов трапеции равна
360
P = AB + BC + CD + AD
4.
BM
A
C
N
D
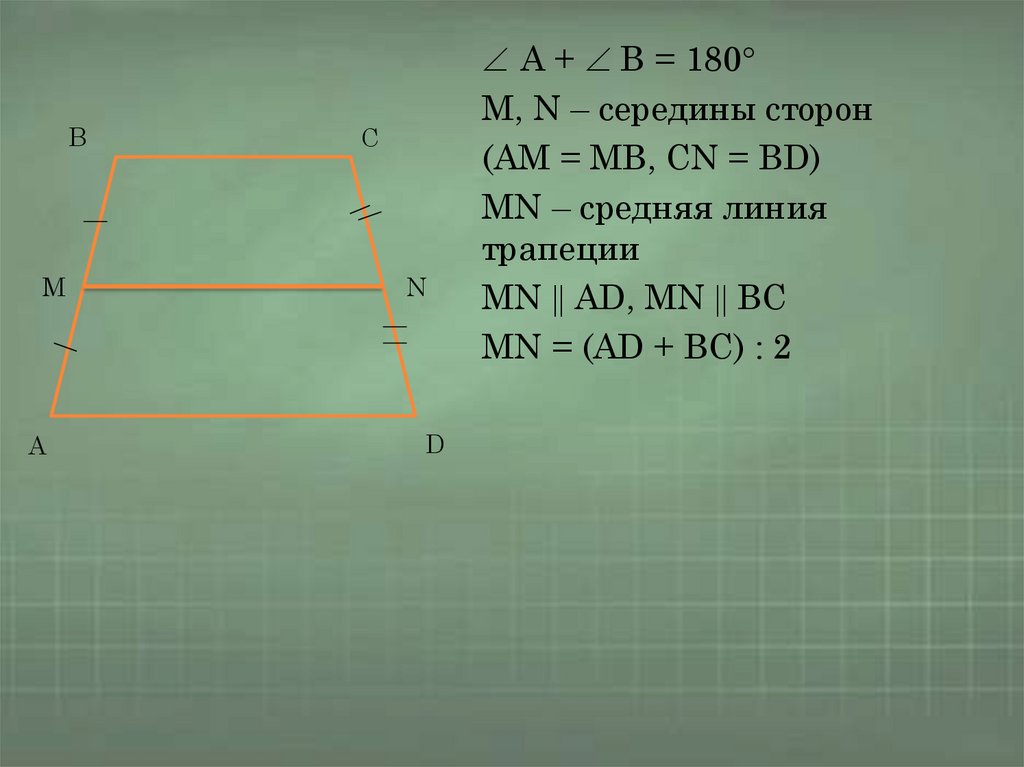
A + B = 180
M, N – середины сторон
(AM = MB, CN = BD)
MN – средняя линия
трапеции
MN AD, MN BC
MN = (AD + BC) : 2
5.
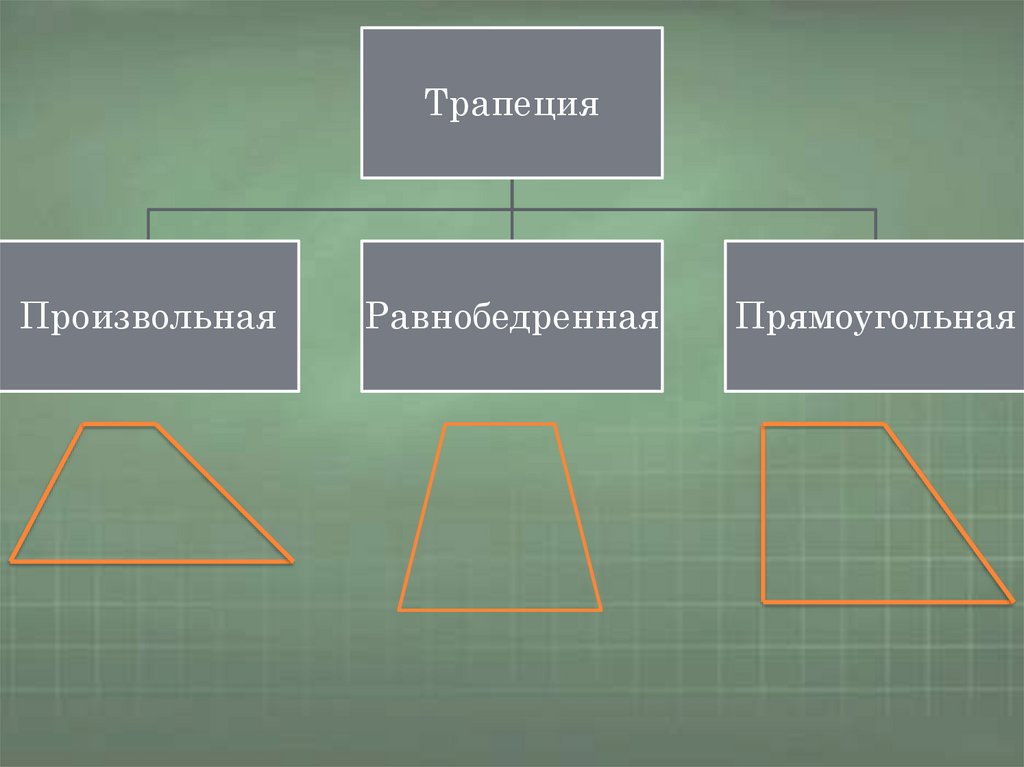
ТрапецияПроизвольная
Равнобедренная
Прямоугольная
6.
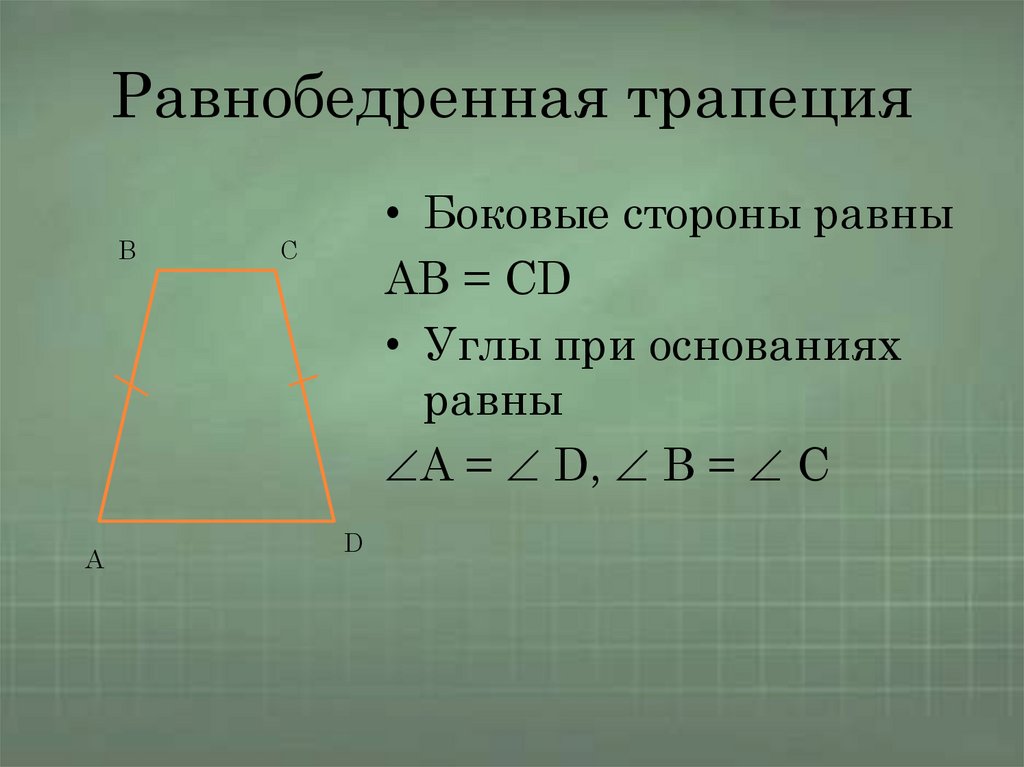
Равнобедренная трапецияB
A
• Боковые стороны равны
AB = CD
• Углы при основаниях
равны
A = D, B = C
C
D
7.
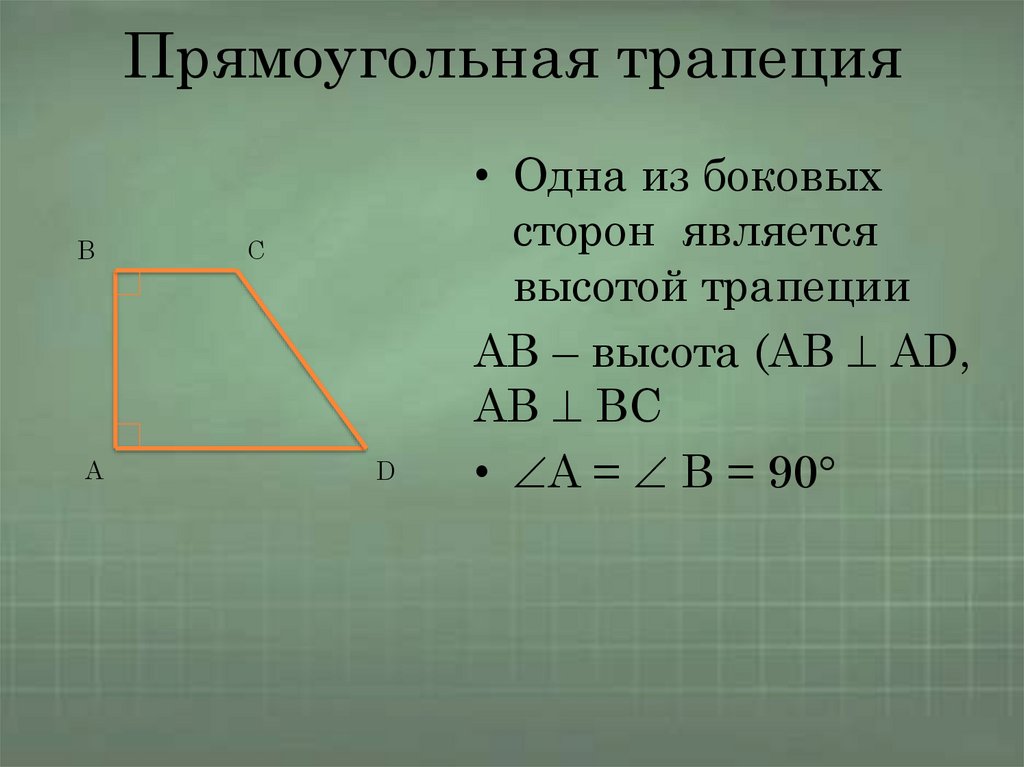
Прямоугольная трапецияB
A
C
D
• Одна из боковых
сторон является
высотой трапеции
AB – высота (AB AD,
AB BC
• A = B = 90
8.
Заполните пропускичетырехугольник
• Трапеция – это _____________,
у которого
параллельны
две стороны ________________,
а две другие
нет.
сумма длин всех сторон
• Периметр – это __________________________
отрезок
• Средняя линия трапеции – это __________,
боковых
соединяющий середины ___________
сторон
9.
Трапеция10.
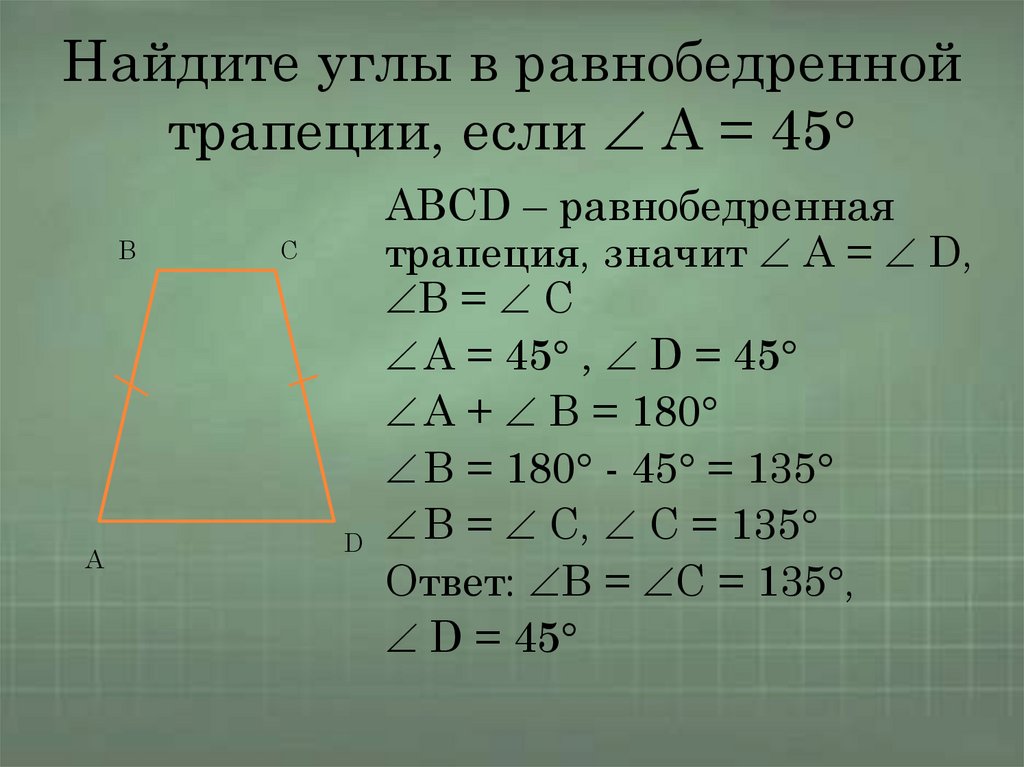
Найдите углы в равнобедреннойтрапеции, если А = 45
B
A
C
D
ABCD – равнобедренная
трапеция, значит A = D,
B = C
A = 45 , D = 45
A + B = 180
B = 180 - 45 = 135
B = C, C = 135
Ответ: B = С = 135 ,
D = 45
11.
Найдите среднюю линию трапеции,если ее основания равны 7 и 9.
ABCD – трапеция, MN –
средняя линия
BC = 7, AD = 9
MN = (7 + 9 ) : 2 = 8
12.
Найдите периметр трапеции, еслиоснования равны 5 и 10, а боковые
стороны 7 и 5
B
A
• ABCD – трапеция
AD = 10, BC = 5, AB = 7,
CD = 5
PABCD = AB + BC + CD +AD
PABCD = 10+5+7+5=27
C
D
Ответ: PABCD = 27
13.
Домашнее задание1. вырезать из цветной бумаги все
изученные виды четырехугольников:
параллелограмм, прямоугольник,
трапеция, квадрат, ромб, произвольный
четырехугольник
2. приклеить их в тетрадь, подписать
название каждого
3. подготовиться к опросу по теме
"Четырехугольники", используя материалы
предыдущих уроков






 Математика
Математика