Похожие презентации:
Призма. Виды призм
1. Презентация на тему: «Призма»
2.
1.) Определение призмы.2.) Виды призм:
- прямая призма;
- наклонная призма;
- правильная призма;
3.) Площадь полной поверхности призмы.
4.) Теорема о площади боковой поверхности призмы.
5.) Объём призмы.
- теорема для треугольной призмы.
- теорема для произвольной призмы.
6.) Сечения призм:
- перпендикулярное сечение призмы;
7.) Призмы встречающиеся в жизни.
3. Определение призмы:
ОПРЕДЕЛЕНИЕ ПРИЗМЫ:4. Основные понятия
ОСНОВНЫЕ ПОНЯТИЯГрани призмы, отличные от оснований, называются боковыми
гранями , а их ребра называются боковыми ребрами . Все
боковые ребра равны между собой как параллельные отрезки,
ограниченные двумя параллельными плоскостями. Все боковые
грани призмы являются параллелограммами.
Соответствующие стороны оснований призмы равны и
параллельны. Поэтому в основаниях лежат равные
многоугольники.
Поверхность призмы состоит из двух оснований и боковой
поверхности.
Высотой призмы называется отрезок, являющийся общим
перпендикуляром плоскостей, в которых лежат основания
призмы.
Высота призмы равна расстоянию h между плоскостями
оснований.
5. Виды призм
ВИДЫ ПРИЗМШестиугольная призма
6.
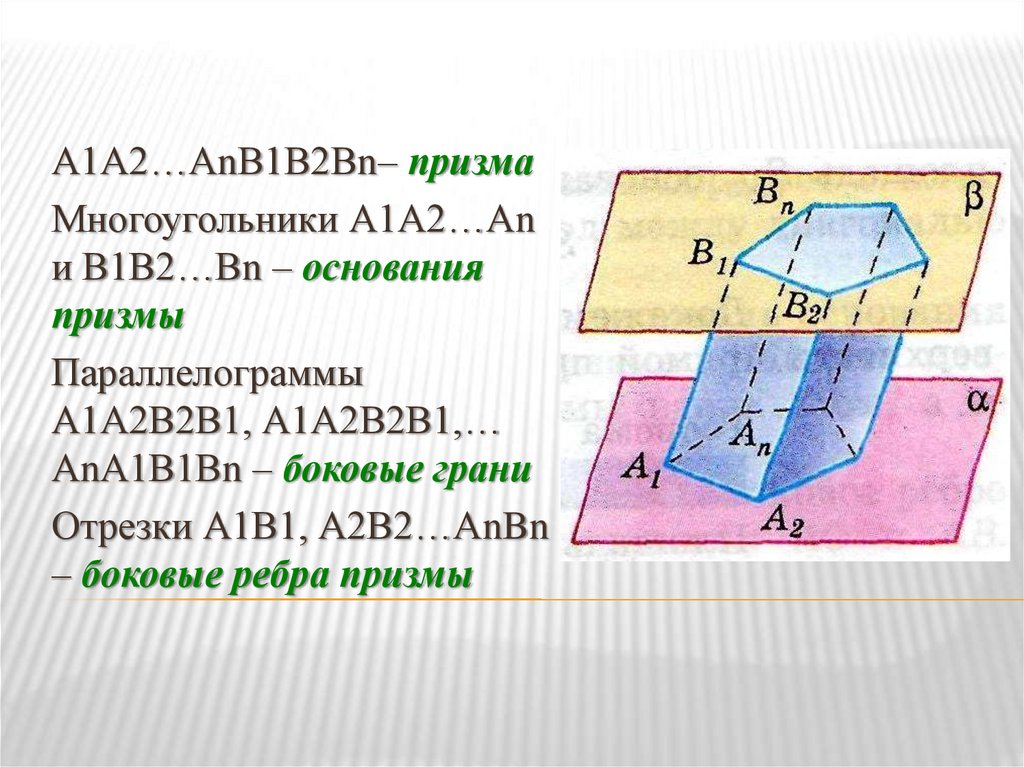
А1А2…АnВ1В2Вn– призмаМногоугольники А1А2…Аn
и В1В2…Вn – основания
призмы
Параллелограммы
А1А2В2В1, А1А2В2В1,…
АnА1В1Вn – боковые грани
Отрезки А1В1, А2В2…АnBn
– боковые ребра призмы
7.
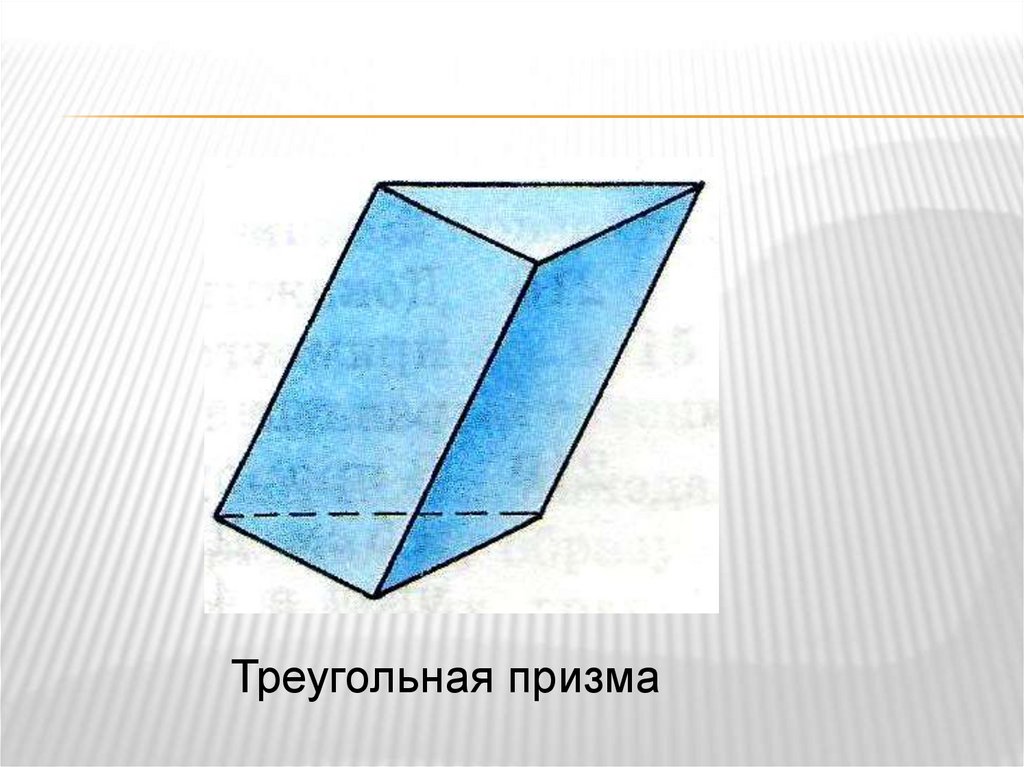
Треугольная призма8.
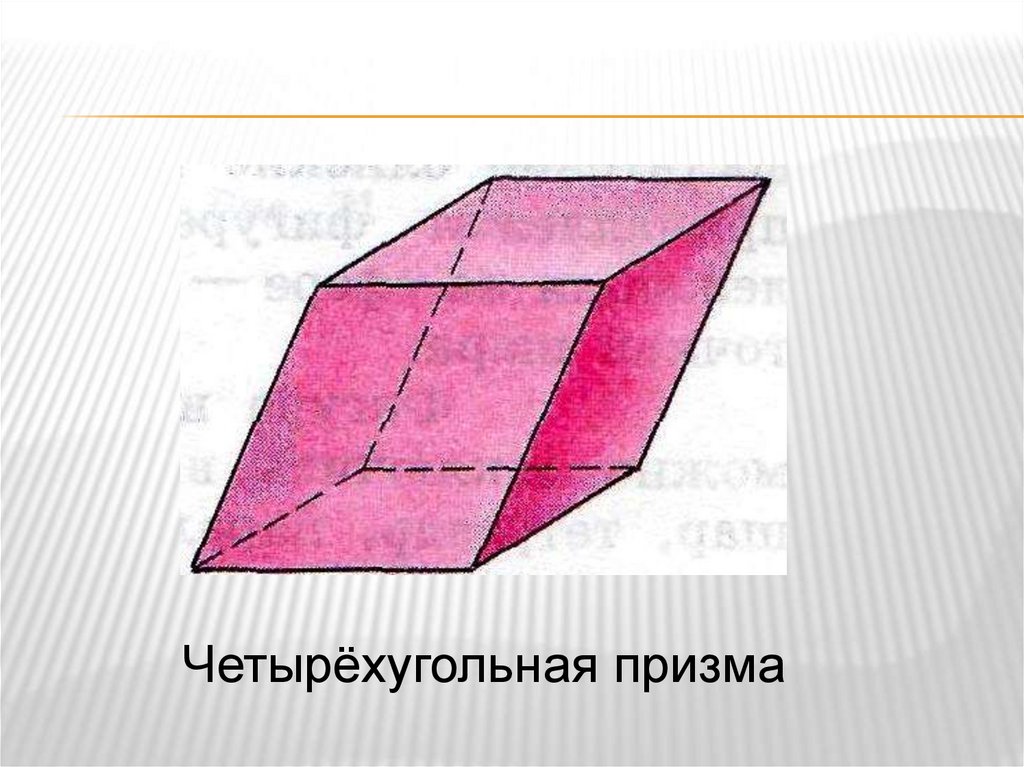
Четырёхугольная призма9. Наклонная и прямая призма
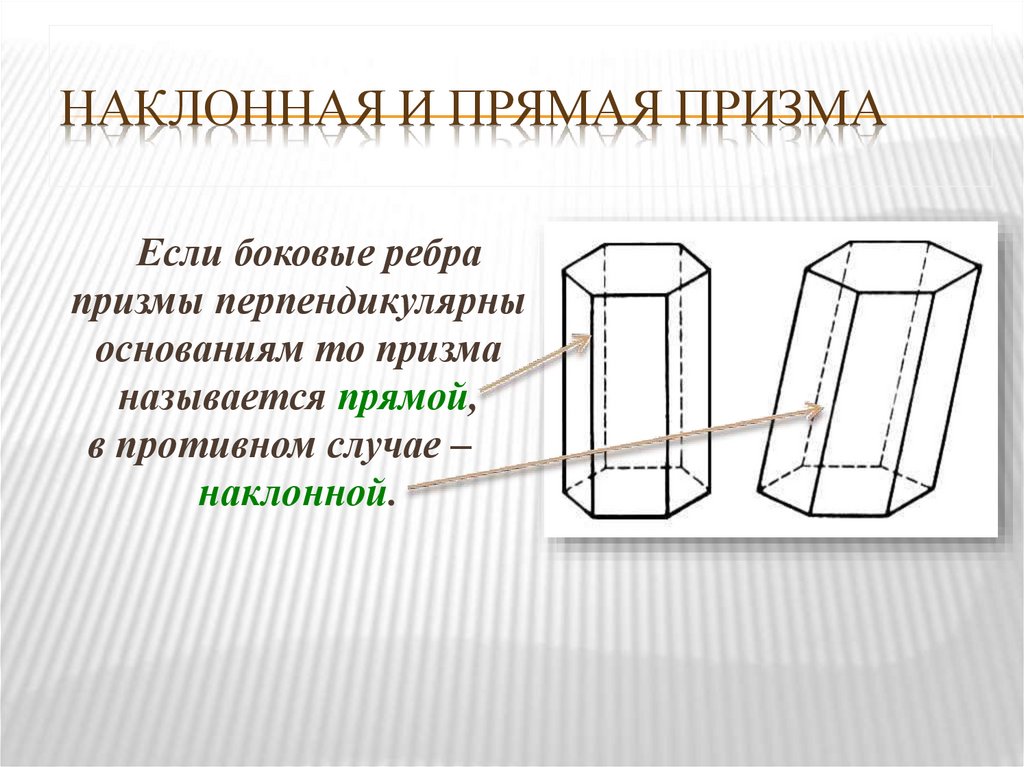
НАКЛОННАЯ И ПРЯМАЯ ПРИЗМАЕсли боковые ребра
призмы перпендикулярны
основаниям то призма
называется прямой,
в противном случае –
наклонной.
10. Правильная призма
ПРАВИЛЬНАЯ ПРИЗМАПризма называется
правильной, если она
прямая и ее основания правильные
многоугольники.
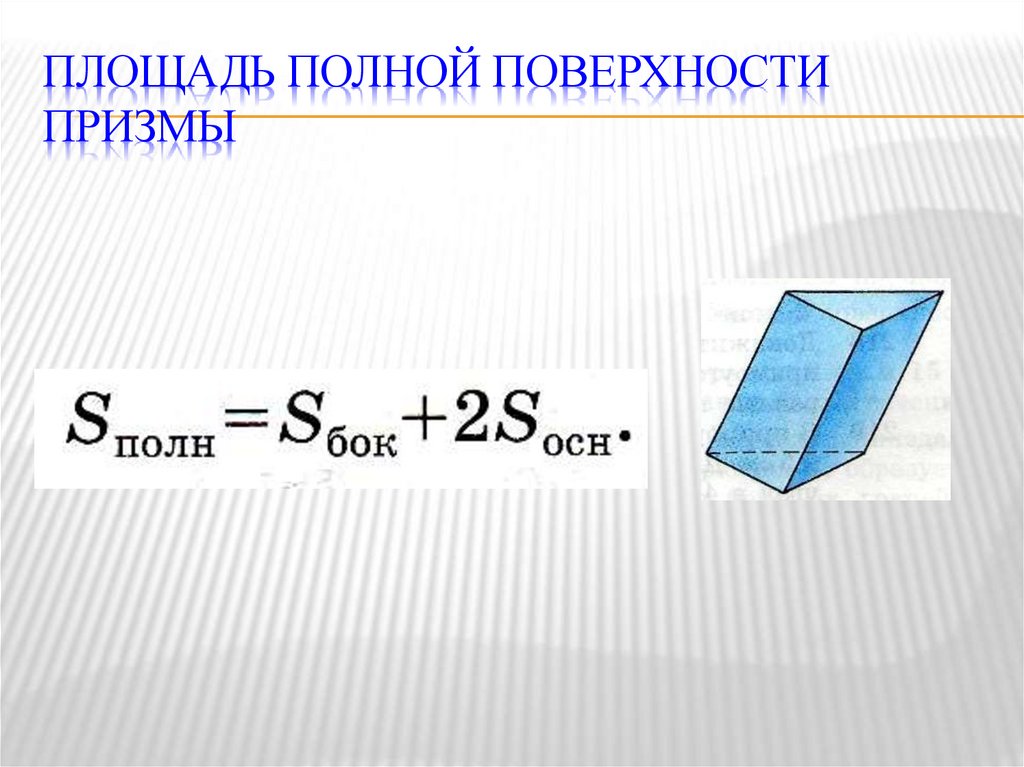
11. Площадь полной поверхности призмы
ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИПРИЗМЫ
12. Площадь боковой поверхности призмы
ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИПРИЗМЫ
ТЕОРЕМА:
Площадь боковой
поверхности прямой
призмы равна
произведению периметра
основания на высоту
призмы.
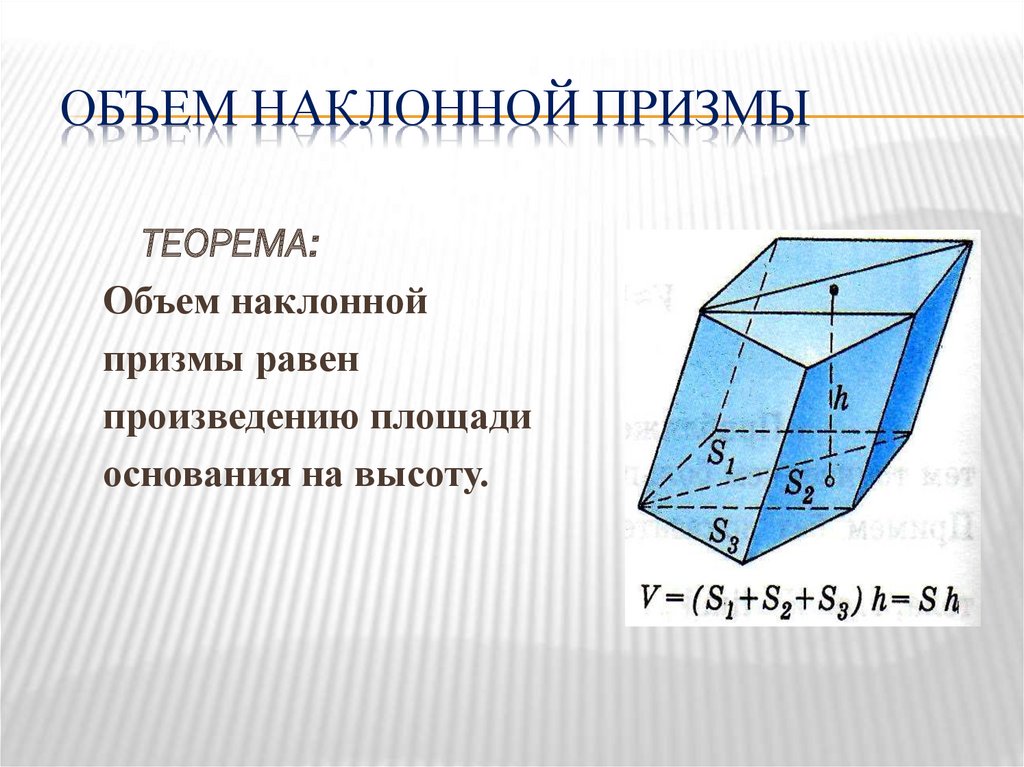
13. Объем наклонной призмы
ОБЪЕМ НАКЛОННОЙ ПРИЗМЫТЕОРЕМА:
Объем наклонной
призмы равен
произведению площади
основания на высоту.
14.
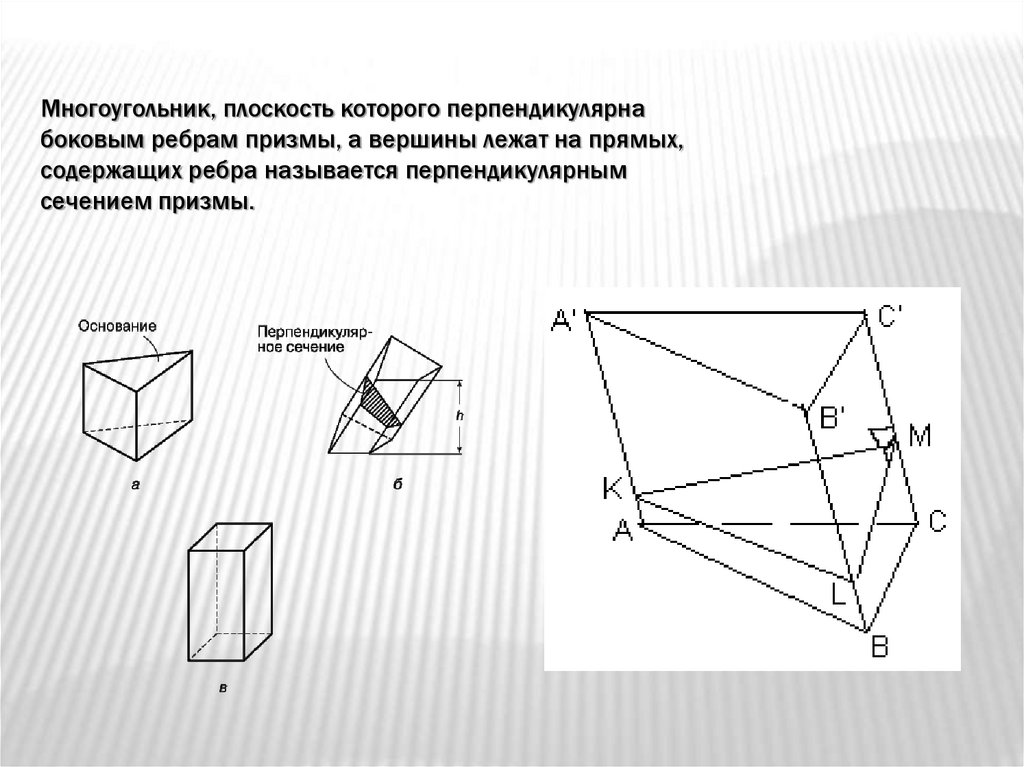
Многоугольник, плоскость которого перпендикулярнабоковым ребрам призмы, а вершины лежат на прямых,
содержащих ребра называется перпендикулярным
сечением призмы.










 Математика
Математика








