Призма, её элементы

1.

Призма, её элементы

2.

Определение призмы:
Призмой называется многогранник, который
состоит из двух плоских многоугольников, лежащих
в разных плоскостях и совмещаемых параллельным
переносом, и всех отрезков, соединяющих
соответствующие точки этих многоугольников.
А1А2…АnВ1В2Вn– призма
Многоугольники А1А2…Аn и
В1В2…Вn – основания призмы
Параллелограммы А1А2В2В1,
А1А2В2В1,… АnА1В1Вn –
боковые грани
Отрезки А1В1, А2В2…АnBn –
боковые ребра призмы

3.

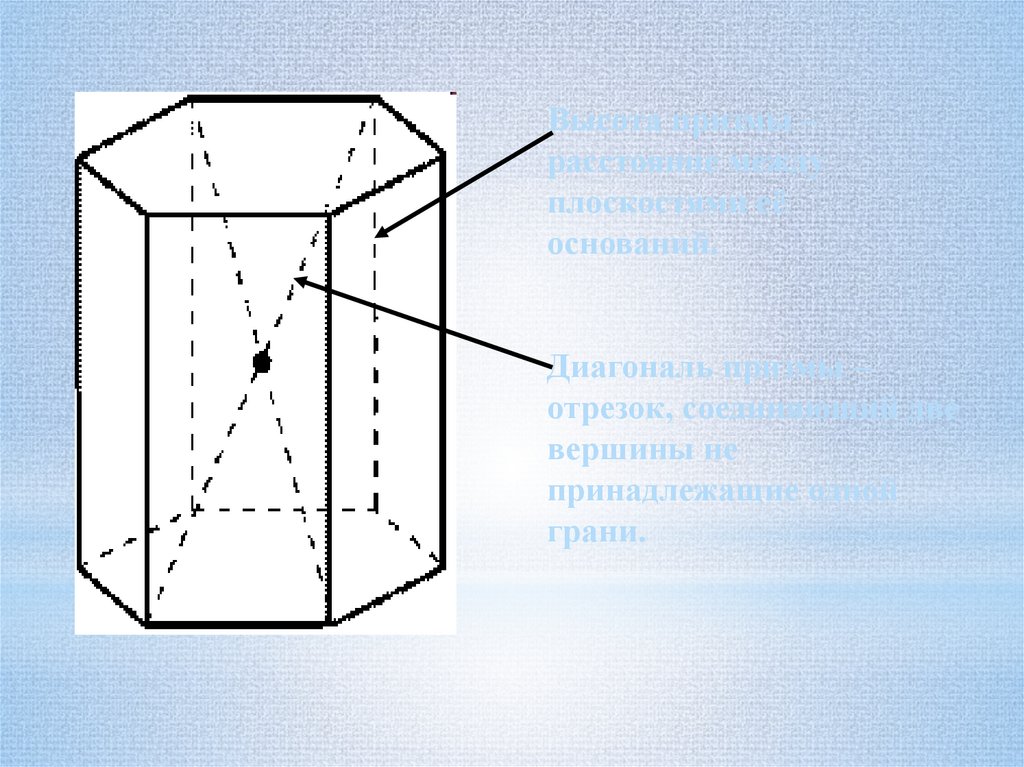
Высота призмы –
расстояние между
плоскостями её
оснований.
Диагональ призмы –
отрезок, соединяющий две
вершины не
принадлежащие одной
грани.

4.

Свойства призмы.
1. Основания призмы являются
равными многоугольниками.
2. Боковые грани призмы являются
параллелограммами.
3. Боковые ребра призмы равны.

5.

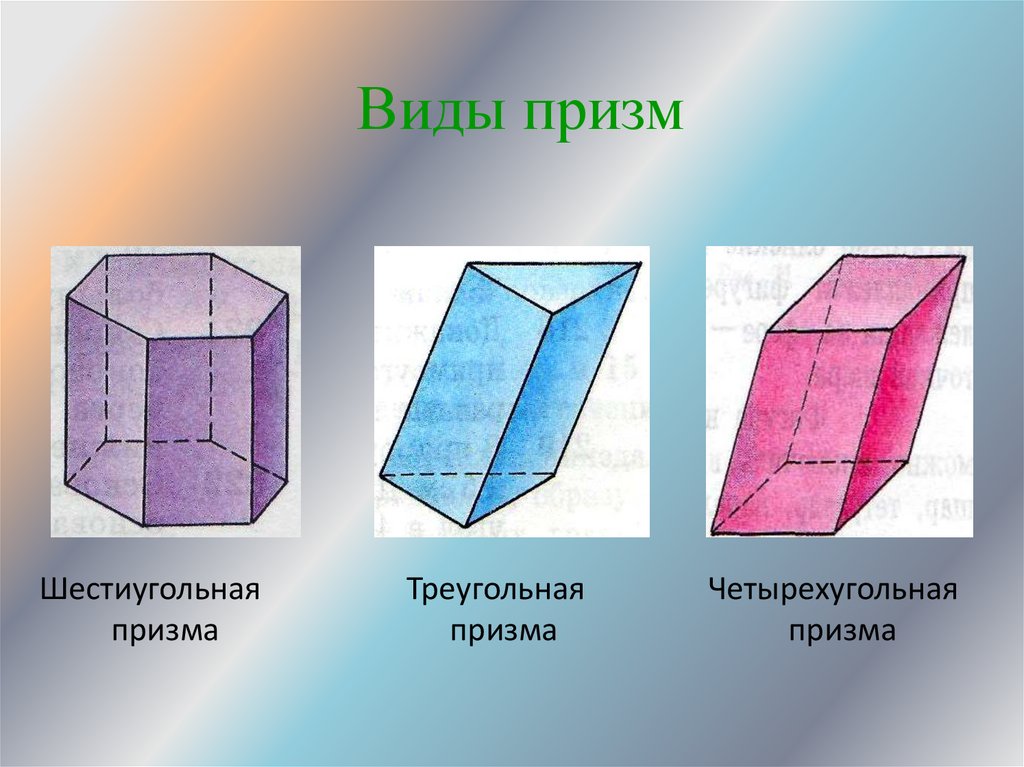
Виды призм
Шестиугольная
призма
Треугольная
призма
Четырехугольная
призма

6.

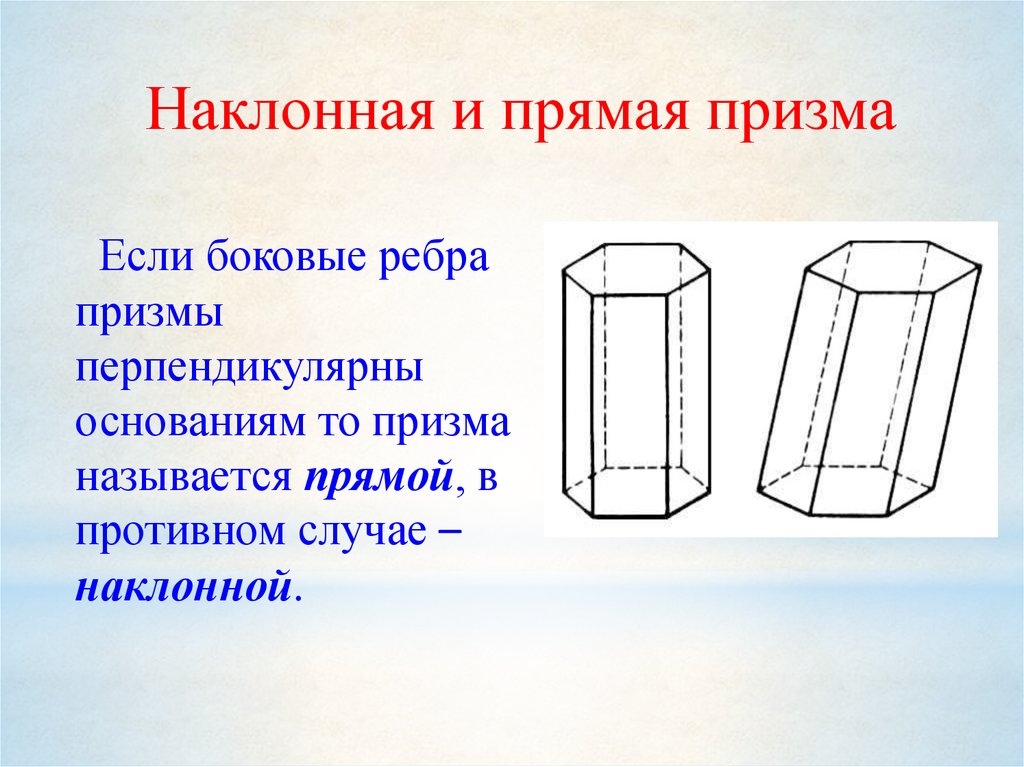
Наклонная и прямая призма
Если боковые ребра
призмы
перпендикулярны
основаниям то призма
называется прямой, в
противном случае –
наклонной.

7.

Правильная призма
Призма называется
правильной, если она
прямая и ее основания правильные
многоугольники.

8.

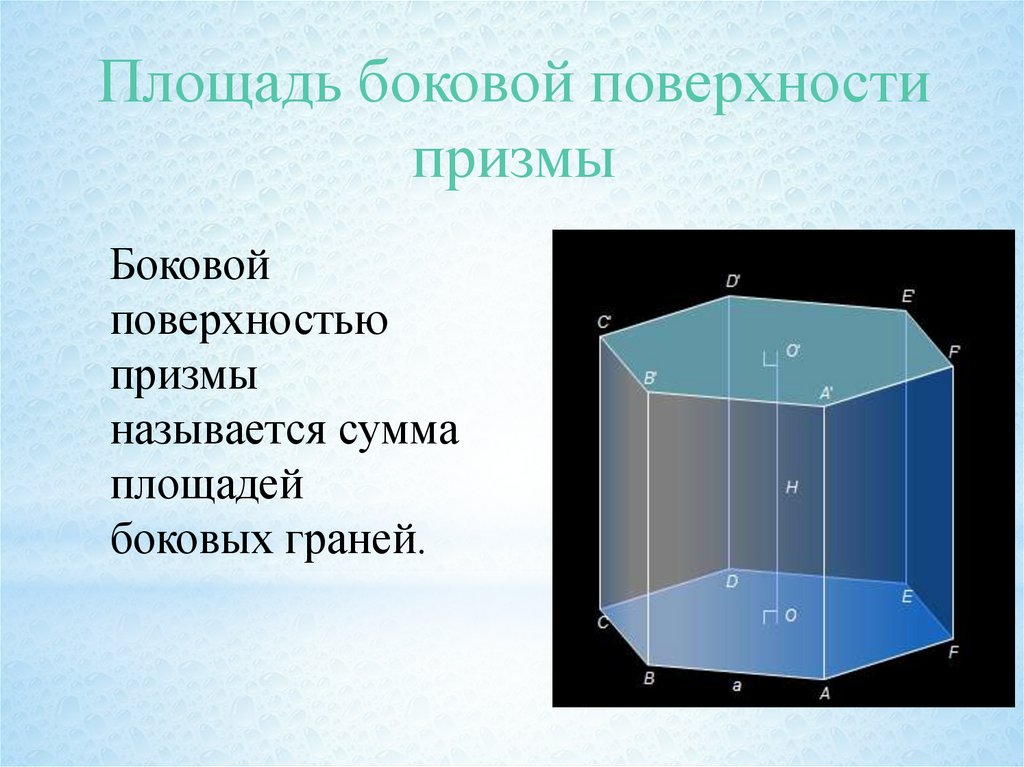
Площадь боковой поверхности
призмы
Боковой
поверхностью
призмы
называется сумма
площадей
боковых граней.

9. Площадь боковой поверхности прямой призмы

*Площадь боковой
поверхности прямой
призмы
*Теорема
* Площадь боковой
поверхности прямой
призмы равна
произведению
периметра основания на
высоту призмы, т.е на
длину бокового ребра.
* Sбок =Pоснования*h

10.

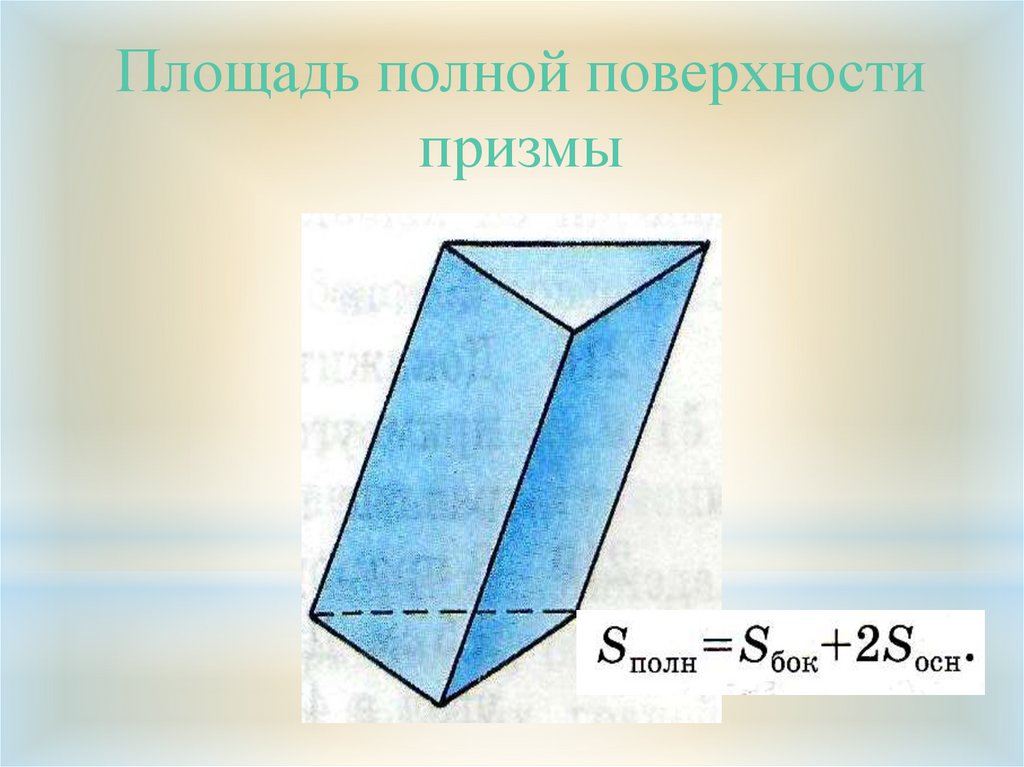
Площадь полной поверхности
призмы

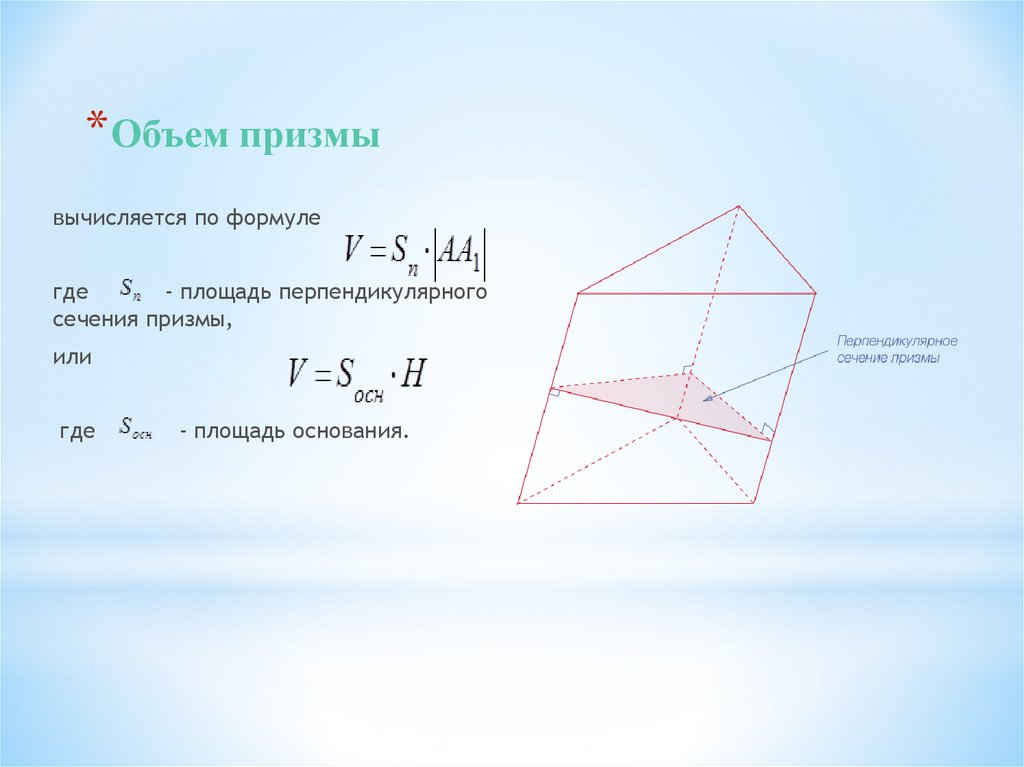
11. Объем призмы

*Объем призмы
вычисляется по формуле
где
- площадь перпендикулярного
сечения призмы,
или
где
- площадь основания.

12.

Выводы
В повседневной жизни нас окружают предметы,
имеющие форму призмы, например, в нашей профессии
форму призмы имеют …
Любая призма имеет следующие элементы…
Практически вычисление площади боковой и полной
поверхностей призмы может пригодиться для …