Логическая интерпретация формулы

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2013

2.

Виды формул в логике предикатов
Под интерпретацией понимается
система М = < M, f >, состоящая из
М={x1,x2…xn} и соответствия f,
сопоставляющего
каждому
предикатному
символу A(n) определенный
n – местный предикат.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
2

3.

Виды формул в логике предикатов
При логической интерпретации формул
логики предикатов возможны три основные
ситуации:
1.В области М для формулы F существует
такая подстановка констант вместо всех
переменных-F=1
формула F называется выполнимой в
области М.
Существует область М, где формула
выполнима
F называется просто выполнимой.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
3

4.

Виды формул в логике предикатов
Пример:
∃x∀y(x≥y)
высказывание,
утверждающее, что в М имеется
единственный максимальный элемент.
На конечном множестве целых чисел
это высказывание истинно.
На множестве двоичных векторов, из
которого удален вектор, состоящий
одних единиц, это высказывание
ложно.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
4

5.

Виды формул в логике предикатов
2.Если
формула F выполнима в М
при любых подстановках
констант,
то
она
называется тождественноистинной в М.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
5

6.

Виды формул в логике предикатов
Пример:
∃xP(x,y) ∀xP(x,y)
Эта формула тождественно истина
для всех М, состоящих из одного
элемента.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
6

7.

Виды формул в логике предикатов
Формула,
тождественноистинная
в
любых
М,
называется
тождественноистинной или общезначимой
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
7

8.

Виды формул в логике предикатов
3)Если формула F невыполнима в
М,
она
называется
тождественно-ложной в М.
Если F невыполнима ни в каких М,
она называется тождественноложной или противоречивой.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
8

9.

Виды формул в логике предикатов
Пример:
a)P1(x,y)&P1(x,z)&P2(x)&P2(y)&P2(z)
– тождественно-ложна на любом
множестве М, если |M|≤2
б)∃x(P(x)&¬(P(x)) –
противоречива(тождественноложна)
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
9

10.

Равносильность формул
Формулы F
G в данной
интерпретации, если на
любом наборе значений
свободных
переменных
они
принимают
одинаковые значения.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
10

11.

Равносильность формул
Формулы F,G равносильны
на множестве М, если они
равносильны
во
всех
интерпретациях, заданных на
множестве М.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
11

12.

Равносильность формул
Формулы F,G равносильны
(в логике предикатов),
если они равносильны на
всех множествах.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
12

13.

Равносильность формул. Примеры
1. На множестве M={a,b} зададим предикаты P1(x,y) и P2(x,y).
x
y
P1(x,y)
x
y
P2(x,y)
a
a
b
b
a
b
a
b
1
0
0
1
a
a
b
b
a
b
a
b
1
1
0
0
Рассмотрим две формулы:
A1 (x1, x2) & A1 (x1, x3)
(1)
A1 (x1, x2) & A1 (x2, x3)
(2)
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
13

14.

Равносильность формул. Примеры
Если область интерпретации –
М и A1 интерпретируется как
предикат P1 , то формулы
(1)
(2) в этой
интерпретации.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
14

15.

Равносильность формул
Если область интерпретации М, А1 интерпретируется как
предикат Р2, то формулы (1)
и (2) не равносильны.
Это пример равносильности в
данной интерпретации.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
15

16.

Равносильность формул
2. Формулы ∀xA(x)
∃xA(x) на одноэлементном
множестве.
Если область интерпретации - одноэлементное множество,
то любой предикат в качестве интерпретации A на этом
множестве принимает значение 1 или 0. В первом случае
обе формулы принимают истинное значение, во втором –
ложное → они равносильны на этом множестве.
Если область интерпретации- двухэлементное
множество{а,в}, то эти формулы не равносильны.
Например,в качестве области интерпретации предикат Р:
Р(а)=1; Р(в)=0.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
16

17.

Равносильность формул. Примеры
3. Пусть предикат P(x, y) - “x
делит y нацело”. Область
интерпретации- N.
Тогда ∀x∃yP(x,y) - “для всех x
существует y такое, что x делит
y”.
Высказывание истинное.
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
17

18.

Равносильность формул. Примеры
Поменяем местами кванторы:
∃y∀xP(x,y)-“существует y такое,
что каждое x делит его.”
Это ложное высказывание.
Среди натуральных чисел такого
числа нет (этим свойством обладает
0, но он не принадлежит N).
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
18

19.

Равносильность формул. Примеры
4. Дан предикат P(x, y) на M={a, b, c, d, e}.
y
x
a
b
c
d
e
a
b
c
d
e
1
1
0
1
0
0
1
1
0
0
1
1
1
0
0
1
1
0
1
1
1
1
0
0
1
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
19

20.

Равносильность формул. Примеры
Образуем
предикатов:
несколько
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
новых
20

21.

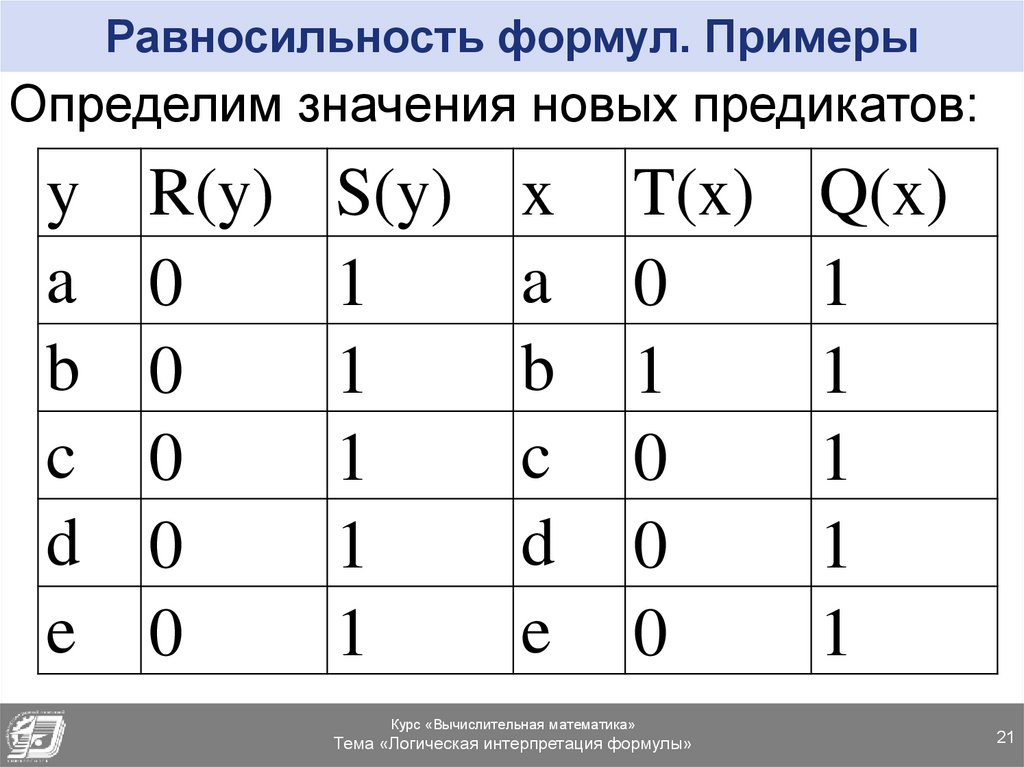
Равносильность формул. Примеры
Определим значения новых предикатов:
y
a
b
c
d
e
R(y)
0
0
0
0
0
S(y)
1
1
1
1
1
x
a
b
c
d
e
T(x)
0
1
0
0
0
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
Q(x)
1
1
1
1
1
21

22.

Равносильность формул. Примеры
Навесим еще по одному квантору
предикаты R(y), S(y), T(x), Q(x).
Результат - все переменные связанные
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
на
22

23.

Равносильность формул. Примеры
Курс «Вычислительная математика»
Тема «Логическая интерпретация формулы»
23

24.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Исенбаева Елена Насимьяновна, 2013