Похожие презентации:
Исследование и построение графиков функции
1. Исследование и построение графиков функции
{ интервалы монотонного возрастания и убывания функции - выпуклость функции на промежутке - точки перегиба асимптоты - построение графика функции }2.
Интервалы монотонного возрастания и убывания функции определяютсязнаком производной.
Если производная f | ( x )
положительна на интервале, то
функция f ( x ) возрастает на нем.
x 0 , f 0 lim
x 0
f
f !( x ) 0
x
Если производная f | ( x ) принимает
отрицательные значения на
интервале, то функция f ( x ) на
нем убывает.
3.
Функция f(x) , определенная и непрерывная в промежутке ( a; b ), называетсявыпуклой (выпуклой вниз), если для любых точек x1 и x2 из ( a; b ), x1 не
равно x2 , выполняется неравенство:
f ( l1 x1 l2 x2 ) l1f ( x1 ) l2f ( x2 )
каковы бы не были положительные числа l1 и l2 , дающие в сумме единицу.
При f ( l1 x1 l2 x2 ) l1f ( x1 ) l2f ( x2 )
функция f(x) называется вогнутой
y
(выпуклой вверх).
f( x )
x1 x 2
f ( x1 ) f ( x 2 )
f(
)
2
2
f ( x2 )
f ( x1 )
(
a
x1
x2
)
b
x
4.
f ( x ) ( f ( x1 )f ( x 2 ) f ( x1 )
( x x1 )) 0
( x 2 x1 )
f ( x ) f ( x1 ) f ( x 2 ) f ( x1 )
0
x x1
( x 2 x1 )
f ( x1 ) f ( c ) 0
|
|
x x1
f | ( x1 ) f | ( c )
0
x1 c
Функция f(x) называется вогнутой
(выпуклой вверх), если f || ( x ) 0
f | ( x1 ) f | ( c )
lim
f || ( c ) 0
x1 c
x1 c
y
Функция f(x) называется выпуклой
(выпуклой вниз), если f || ( x ) 0
c ( x1 , x2 )
f ( x ) Y ( x )
f( x )
f ( x2 )
f ( x1 )
0
x1
x
x2
5.
Теорема. Для выпуклости (вогнутости) функции y = f(x) в промежутке (a,b)необходимо и достаточно, чтобы здесь выполнялось неравенство
f || ( x ) 0 ( f || ( x ) 0 ) .
Точку M(x0 ;f(x0)) кривой y = f(x) называют её точкой перегиба, если она
отделяет участок графика, где он выпуклый, от участка, где график
функции f(x) вогнут.
В точке перегиба вторая производная функции обращается в ноль.
Достаточным условием существования точки перегиба является смена
знака f || ( x ) при переходе через неё.
f || ( x0 ) 0 f ( x )
y
f || ( x0 ) 0
f || ( x0 ) 0
x
x0
6.
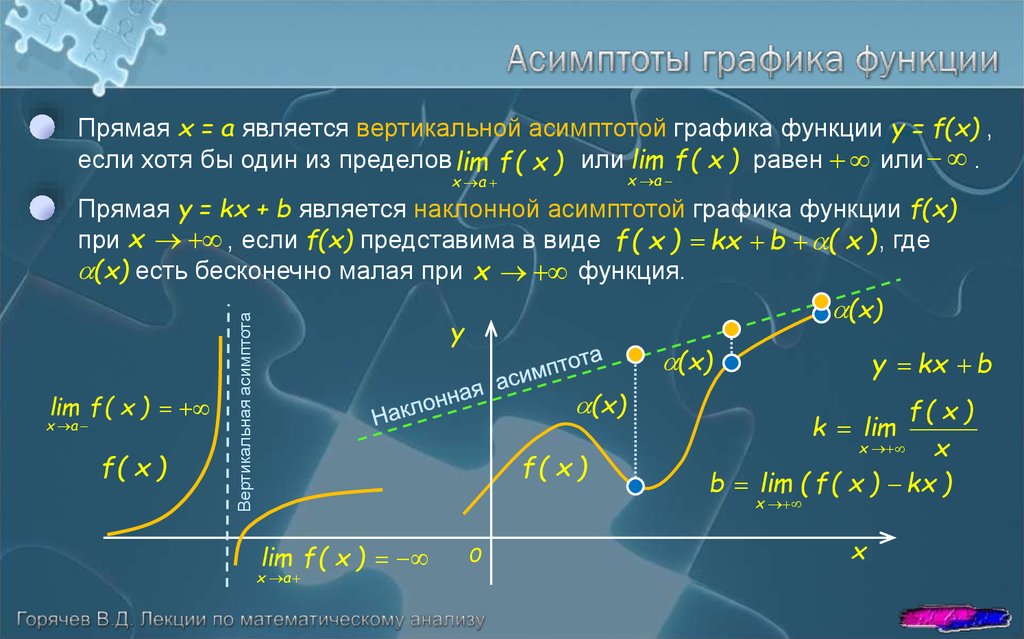
Прямая x = a является вертикальной асимптотой графика функции y = f(x) ,если хотя бы один из пределов lim f ( x ) или lim f ( x ) равен или .
x a
x a
Прямая y = kx + b является наклонной асимптотой графика функции f(x)
при x , если f(x) представима в виде f ( x ) kx b a( x ) , где
a(x) есть бесконечно малая при x функция.
f( x )
Вертикальная асимптота
lim f ( x )
x a
a(x)
y
a(x)
a(x)
f( x )
y kx b
f( x )
x
x
b lim ( f ( x ) kx )
k lim
x
lim f ( x )
x a
0
x
7.
Для построения рекомендуется следующая последовательность действий.• Найти множество определения функции, области непрерывности, точки разрыва.
• При построении графика учитывать такие свойства, как четность, нечетность,
периодичность.
• Найти асимптоты графика функции.
• Найти точки пересечения графика с осями координат.
• Найти первую и, если нужно, вторую производную функции. Найти точки в которых
первая и вторая производные либо не существуют, либо обращаются в нуль.
• Составить таблицу изменения знака функции, первой и второй производных.
Определить промежутки возрастания и убывания функции, выпуклости и
вогнутости функции, найти точки экстремума и точки перегиба, вычислить
значения функции в этих точках.
• Окончательно вычертить график функции.
8.
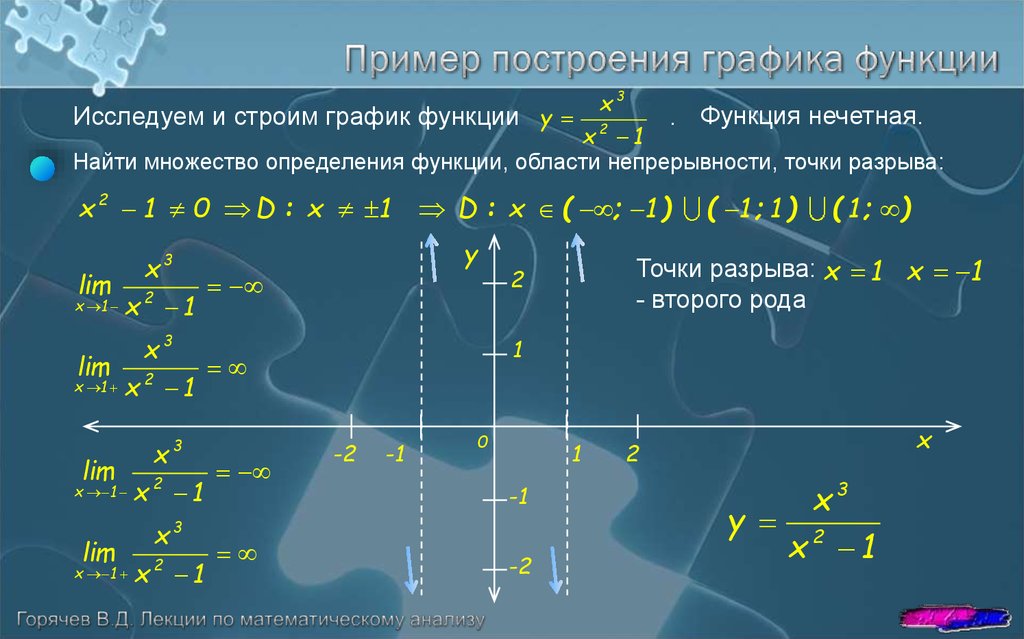
x3Исследуем и строим график функции y 2
. Функция нечетная.
x 1
Найти множество определения функции, области непрерывности, точки разрыва:
x 2 1 0 D : x 1 D : x ( ; 1 )
y
x3
lim 2
x 1 x
1
x3
lim 2
x 1 x
1
x3
lim 2
x 1 x
1
( 1 ; )
Точки разрыва: x 1 x 1
- второго рода
2
x3
lim 2
x 1 x
1
( 1 ; 1 )
1
-2
-1
0
1
-1
-2
x
2
x3
y 2
x 1
9.
Найти нули функции, наклонные (горизонтальные) асимптоты.x3
y 2
x 1
y
y
x x x x( x 1 ) x
x
x
x2 1
x2 1
x 2 1
3
2
x3
y( 0 ) 2
0
x
0
x 1
y kx b
f( x )
x3
k lim
lim
1
2
x
x x ( x
x
1 )
x3
b lim ( f ( x ) kx ) lim 2
x
x
x x
1
x
lim 2
0
x x
1
y x
2
1
-2
-1
0
-1
-2
1
2
x
x3
lim 2
x x
1
10.
Найти первую производную функции. Найти точки в которых перваяпроизводная либо не существует, либо обращается в нуль. Найти точки
экстремума.
|
y
x 3 3x 2( x 2 1 ) x 3( 2x )
2
2
2
2
x
1
(
x
1
)
x 3x
x ( x 3 )
( x 2 1 )2 ( x 1 )2( x 1 )2
4
2
2
2
y ( 1 )
x 2( x 2 3 )
|
y (x)
0
( x 1 )2( x 1 )2
x 2 ( x 2 3 ) 0 x1 ,2 0 , x3 ,4 3
y| 0
y| 0
|
1
-1.72
-2
|
|
y| 0 y| 0 y| 0 y 0 y 0
-1
1.72
0
-1
-2
1
x3
y 2
x 1
2
y( 0 ) 0
y( 3 )
x
3 3
2
11.
Найти вторую производную функции. Найти точки в которых втораяпроизводная либо не существует, либо обращается в нуль. Найти
промежутки выпуклости, точки перегиба.
y
4
2 |
3
x 3x
2 x 6x
y (x) 2
2
2
3
( x 1 )
( x 1 )
2 x( x 2 3 )
||
y
( 1 )
( x 1 )3( x 1 )3
-1.72
||
x ( x 2 3 ) 0 x1 0 , x3 ,4 i 3 -2
y ( x 1 ) 0
y ( 1 x 0 ) 0
y || ( 0 x 1 ) 0
y || ( x 1 ) 0
||
||
-1
2
1
1.72
0
-1
-2
1
2
x3
y 2
x 1
x
12.
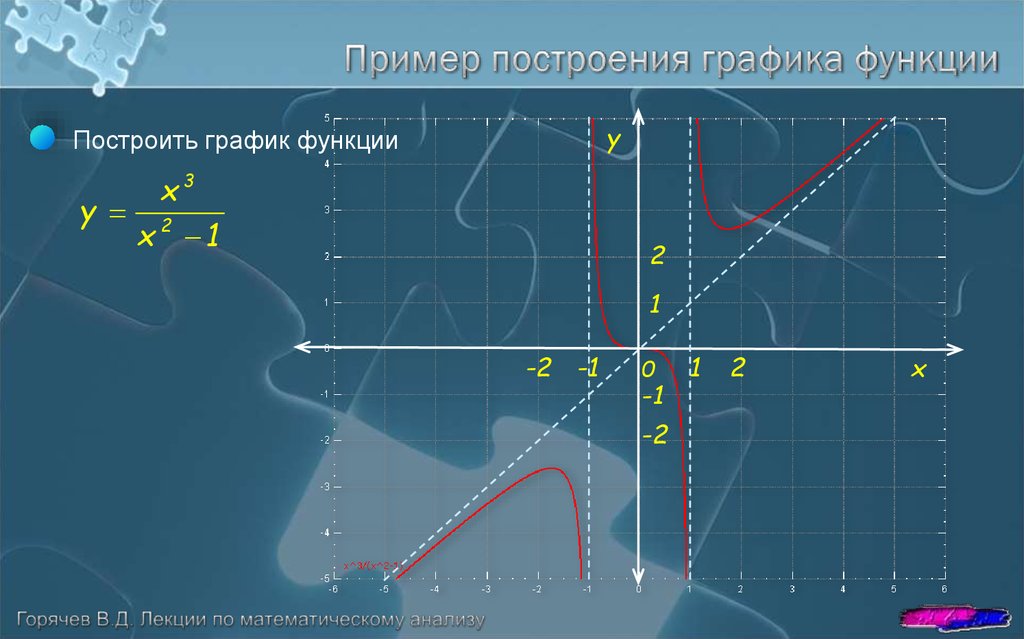
yПостроить график функции
x3
y 2
x 1
2
1
-2 -1
0
-1
-2
1
2
x









 Математика
Математика








