Похожие презентации:
Элементы векторной алгебры
1. Элементы векторной алгебры
12. Векторы
Понятие вектора. Операции с векторами.Линейная независимость системы векторов.
Понятие базиса.
Декартова система координат.
Проекция вектора на ось
Длина вектора
Направляющие косинусы вектора
Действия над векторами в координатной форме
Координаты вектора
Скалярное произведение
Векторное произведение
Смешанное произведение
2
3. Понятие вектора. Операции с векторами
Вектор –это направленный прямолинейный отрезок (т.е. отрезок,имеющий определенную длину и определенное направление).
a
A
B
Расстояние от начала вектора до его
конца называется длиной или модулем
вектора и обозначается AB или a .
Вектор, длина которого равна единице, называется единичным
вектором или ортом.
Вектор, начало и конец которого совпадают, называется нулевым и
обозначается 0 . Нулевой вектор не имеет определенного направления и
имеет длину, равную нулю.
3
4.
ab
a
b
Три вектора, лежащие в одной или в параллельных плоскостях,
называются компланарными.
4
5.
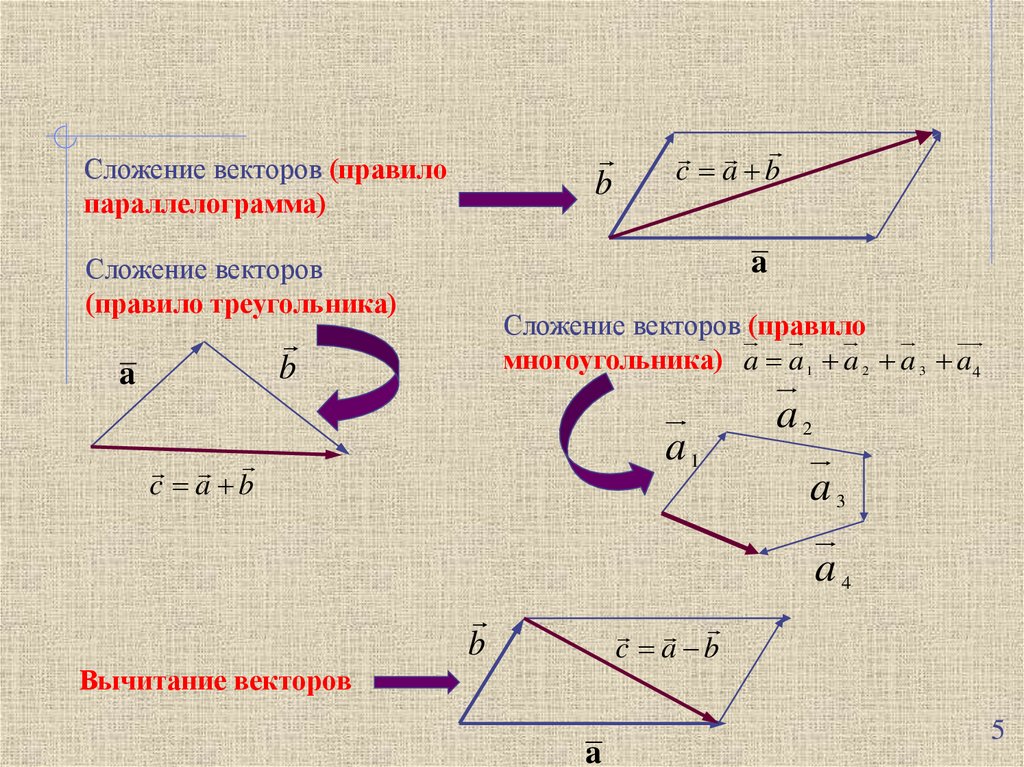
bСложение векторов (правило
параллелограмма)
a
Сложение векторов
(правило треугольника)
Сложение векторов (правило
многоугольника) a a 1 a 2 a 3 a4
b
a
c a b
a1
c a b
a2
a3
a4
b
c a b
Вычитание векторов
a
5
6.
Произведением вектора a на число 0 называется вектор, длинакоторого a , а направление совпадает с направлением вектора a
при 0 и противоположно ему при 0 .
2a
a
2a
При умножении вектора на (-1) получается противоположный вектор
a ( 1) a
Если два ненулевых вектора коллинеарны то один из них можно
выразить через другой
a b
6
7. Линейная независимость системы векторов. Понятие базиса
Совокупность векторов называется линейно зависимой, еслилинейная комбинация этих векторов равна нулю, причем не все
коэффициенты линейной комбинации равны нулю одновременно.
a 1 a 1 2 a 2 3 a 3 ... n an 0
Совокупность векторов называется линейно независимой, если
линейная комбинация этих векторов не равна нулю, причем равенство
нулю возможно только в том случае, если все коэффициенты линейной.
комбинации равны нулю одновременно.
a 1 a 1 2 a 2 3 a 3 ... n an 0
Если векторы линейно зависимы, то один из них можно представить
в виде линейной комбинации остальных.
7
8.
Три ненулевых вектора линейно зависимы тогда и только тогда,когда они компланарны. В этом случае третий вектор является
линейной комбинацией двух других
.
c a b
Два ненулевых вектора линейно зависимы тогда и только тогда,
когда они коллинеарны
a b
Базисом векторного пространства называется совокупность
линейно независимых векторов, количество которых определяется
размерностью пространства. Любой небазисный вектор является
линейной комбинацией базисных.
8
9.
В одномерном пространстве - один базисный вектор a, остальныевекторы можно записать в виде b a
Все такие векторы будут лежать на одной прямой с вектором a .
Таким образом, одномерное пространство – это пространство
коллинеарных векторов.
В двумерном пространстве на плоскости будет два базисных вектора
a и b , а любой третий вектор равен их линейной комбинации
Такой вектор является
диагональю
параллелограмма, построенного
на векторах a и b . Т.е. все три вектора будут компланарны.
c a b
В трехмерном пространстве – три базисных
а любой четвертый
вектора,
можно представить в виде d a b c
c
a
b
, d a b c
Выражения вида b a ,
называются разложениями вектора по базису, а коэффициенты
разложения - координатами вектора в данном базисе.
9
10.
Декартовой прямоугольной системой координат в пространственазывают систему координат, базисом в которой являются единичные
векторы, попарно ортогональные друг с другом.
Правую систему координат, в которой векторы базиса образуют
правую тройку, обозначают i, j, k.
Z
az
Пусть a – произвольный вектор.
a
Тогда
a = ax i + ay j+ az k
или
a ={ a x , a y , a z }
ay
k
i
X
ax
j
Y
10
11.
Проекция вектора на осьПусть в пространстве задана ось l, то есть направленная прямая, AB произвольный вектор.
Обозначим через A1 и B1 - проекции на ось l точек А и В соответственно.
B
B
A
A
B1 A1 A1
l
B1
Проекцией вектора АВ на ось l называется положительное число A1 B1
если вектор A1 B1 и ось l одинаково направлены, и отрицательное число
A1 B1 , если вектор A1 B1 и ось l противоположно направлены.
Если точки A1 и B1 совпадают, то проекция вектора AB равна 0.
11
,
12.
Свойства проекций:Проекция вектора a на ось l равна произведению длины вектора a
на косинус угла между вектором и осью: прl a a cos
Проекция суммы нескольких векторов на ось l равна сумме их
проекций на эту ось.
При умножении вектора a на число его проекция на ось l также
умножается на это число: прl ( a) прl a
Вектор можно представить в виде a ax i a y j az k , где
координата
ax - это проекция вектора
a на ось Ох,
координата a y - это проекция вектора a на ось Оy,
координата az - это проекция вектора a на ось Оz.
12
13.
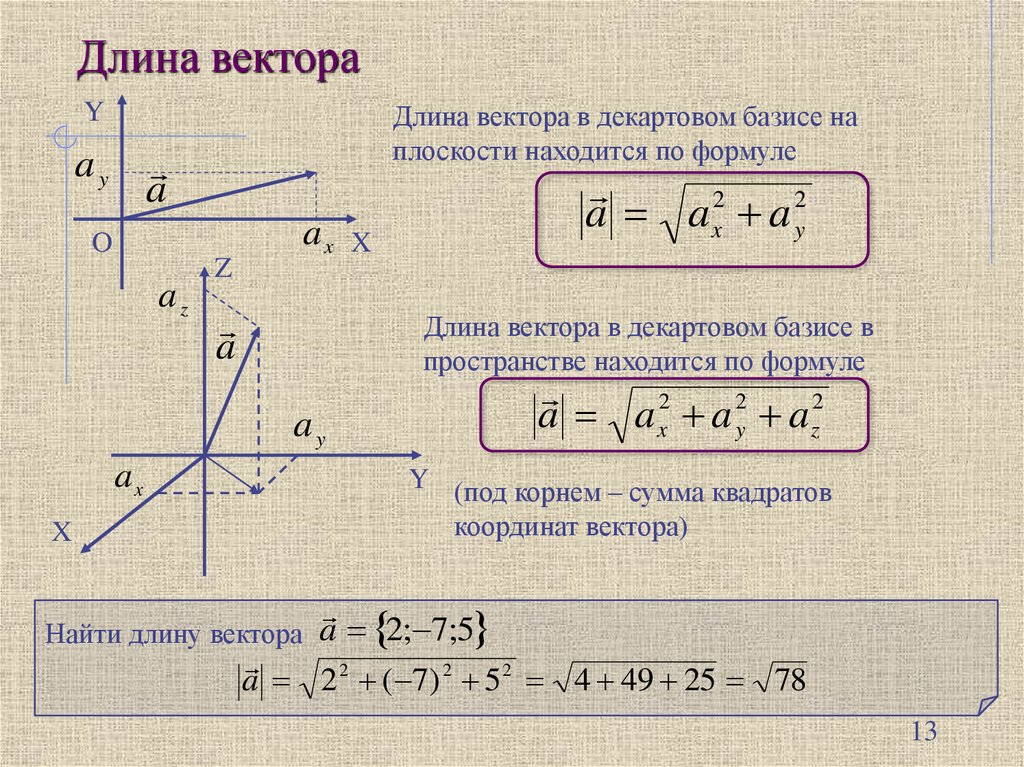
Длина вектораДлина вектора в декартовом базисе на
плоскости находится по формуле
Y
a
ay
O
az
Z
ax X
a
Длина вектора в декартовом базисе в
пространстве находится по формуле
ay
ax
X
a a x2 a y2
2
2
2
a ax a y az
Y (под корнем – сумма квадратов
координат вектора)
Найти длину вектора a 2; 7;5
a 2 2 ( 7) 2 5 2 4 49 25 78
13
14.
Направляющие косинусы вектораПусть задан вектор a ={ a x , a y , a z }.
Рассмотрим вектор cos , cos , cos
Z
ПоПо
свойству
проекций
свойству
1 проекций
ax прOx a a cos ,
a
a y прOy a a cos ,
Y
X
az прOz a a cos
ay
a
ax
1
{ cos , cos , cos }= i + j + z k = a ,
a
a
a
a
направляющие
косинусы
вектора
косинусы
вектора
cos , cos , cos -–направляющие
a
a.
направляющих
косинусов, то есть вектор
свойство
направляющих
cos 2 cos 2 cos 2 1 -–свойство
и направлен также, как и a .
cos , cos , cos - единичный
косинусов.
Вектор cos , cos , cos называют ортом вектора a .
14
15.
Действия над векторами в координатной формеПусть
Пусть a ={ a x , a y , a z }, b ={ bx , by , bz }.
1. Сложение векторов
a b a x bx ; a y b y ; a z bz
2. Вычитание векторов
a b a x bx ; a y b y ; a z bz
3. Умножение вектора на число
b a = { a x , a y , a z }
4. Линейная комбинация векторов
a b a x bx ; a y b y ; a z bz
Условие коллинеарности векторов в координатной форме
Если два вектора коллинеарны, то b a
тогда
bx a x откуда
b y a y
b a
z
z
ax a y az
bx b y bz
Координаты коллинеарных векторов пропорциональны.
15
16.
Координаты вектора, заданного начальнойи конечной точками
Пусть известны координаты начала и конца вектора A (x1, y1, z1), B (x2, y2, z2).
Y
Найдем координаты AB .
A
Вектор AB = OB – OA .
B
O
X
Векторы, выходящие из начала координат
в какую-либо точку, называются
радиус-векторами этой точки.
Координаты радиуса-вектора точки совпадают с координатами
самой точки, поэтому
O B ={x , y , z },
2 2 2
O A ={ x , y , z },
1 1 1
И тогда AB = {x – x , y – y , z – z } .
2
1 2
1 2
1
Координаты вектора равны разности соответствующих координат
конечной и начальной точек.
16
17. Расстояние между двумя точками
Если требуется найти расстояние между точками A( x1 ; y1 ; z1 ) иB ( x2 ; y 2 ; z 2 ) , то можно образовать вектор
AB x2 x1 ; y2 y1 ; z 2 z1 и найти его длину по формуле
d AB ( x2 x1 ) 2 ( y 2 y1 ) 2 ( z 2 z1 ) 2
Найти расстояние между точками
A(5; 3;1) и B(3;6; 2)
d AB ( 2) 2 9 2 ( 3) 2 4 81 9 94
17
18.
Скалярное произведение векторовСкалярным произведением двух ненулевых векторов a и b
называется число, равное произведению их длин на косинус угла между
ними. Записывают a b или (a , b ).
b
пр a b
a
пр b a =| a | cos ( a , b ) = b пр a b
пр a b =| b | cos ( a , b ) = a пр b a
( a , b ) = a пр a b = b пр b a
Найти скалярное
если известно:
произведение векторов,
a 3 , b 4 , 120o
(a b ) a b cos 3 4 cos 120 o 12 ( 0,5) 6
18
19.
Свойства скалярного произведения1.
2.
3.
4.
Если два вектора перпендикулярны, то есть a b , то их
5. Если два вектора коллинеарны, то их скалярное произведение
равно произведению длин векторов. При этом произведение
положительно, если векторы сонаправлены, и отрицательно, если
направления противоположные
(a b ) a b
В частности, скалярное произведение вектора самого на себя равняется
скалярному квадрату вектора и равняется квадрату его длины
a a a 2 a 2
19
20.
Скалярное произведение в координатной формеСкалярное произведение в координатной форме равно сумме
произведений соответствующих координат
( a , b ) = a x b x + a y b y + a z bz .
Найти скалярное произведение векторов a 2; 7;5 и b 3;0; 4
(a b ) 2 ( 3) ( 7) 0 5 ( 4) 6 0 20 26
Применение скалярного произведения
Скалярное произведение применяется для нахождения:
1. Длины вектора
2. Проекции вектора на вектор
3. Косинуса угла между векторами
4. Проверки условия перпендикулярности векторов
5. Работы силы по перемещению точки
20
21.
Векторное произведение векторовВекторным произведением двух ненулевых векторов a и b
называется вектор c , для которого выполняются следующие условия:
Вектор c перпендикулярен вектору a и вектору b ,
т.е. перпендикулярен
плоскости, в которой лежат эти векторы.
Длина вектора c равна произведению длин векторов
на синус угла между векторами
c | a b | a b sin
Вектор c направлен так, что из его
конца кратчайший
поворот от вектора a к вектору b виден против часовой стрелки
c a b
b
Обозначения векторного произведения
c a b
или [ a , b ]
a
21
22.
Векторные произведения векторов декартового базиса[i , j] = k
[ j,k] = i
[i ,k] = – j
[ j, i ] = –k
[k, j] = –i
[ k , i ]= j
Свойства векторного произведения
1.
[a,b] = – [b,a]
2.
[ a , b ] = [ a , b ] = [ a , b ]
3.
[ a1 + a2 , b ] = [ a1 , b ] + [ a2 , b ]
4.
Векторное произведение двух коллинеарных векторов равно нулю.
В частности, если векторным образом перемножать вектор сам
на себя, получится [ a , a ] = 0
22
23.
Векторное произведение в координатной формеi
[ a , b ] = ax
bx
j
ay
by
k
az
bz
ay
[a,b] = i
by
az
ax
– j
bz
bx
ax
az
+k
bx
bz
ay
by
Векторное произведение в координатной форме представляет собой
определитель третьего порядка, в первой строке которого стоят
базисные векторы декартовой системы координат, а во второй и третьей
строках – координаты перемножаемых векторов.
Найти векторное произведение векторов a 2; 7;5 и b 3;0; 4
Составляем определитель и раскладываем его по элементам первой
строки
i
j
k
2 7 5 i ( 7) ( 4) 5 0 j (2 ( 4) 5 ( 3)) k (2 0 ( 7) ( 3)) 28 i 7 j 21 k
3 0 4
23
24.
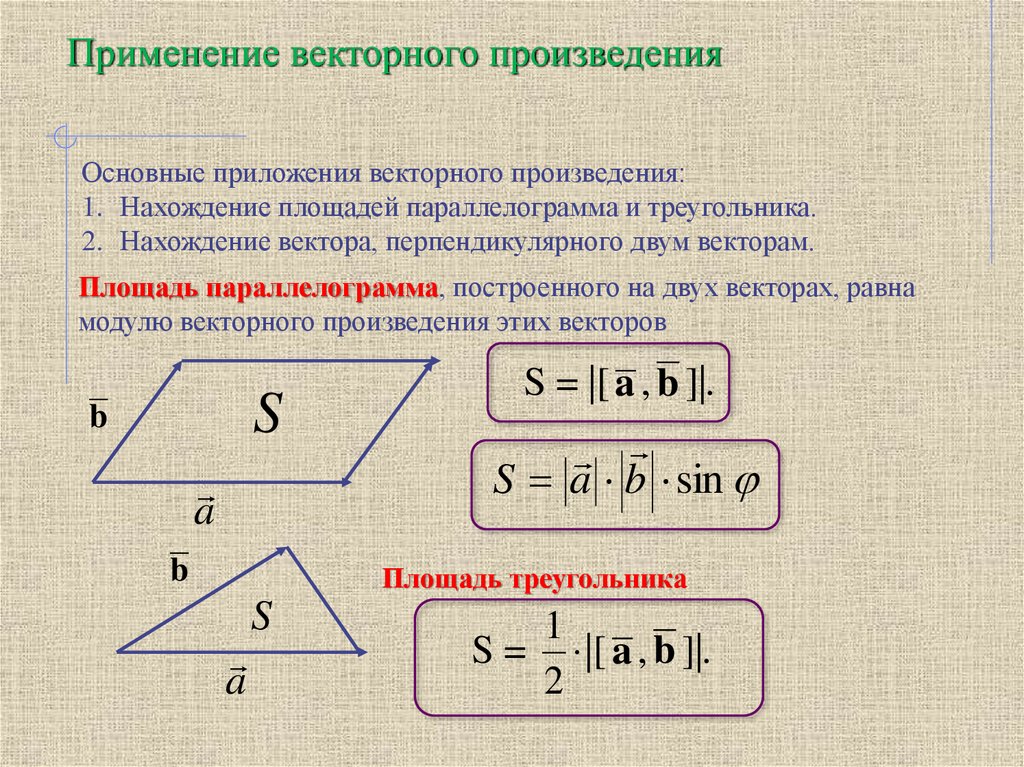
Применение векторного произведенияОсновные приложения векторного произведения:
1. Нахождение площадей параллелограмма и треугольника.
2. Нахождение вектора, перпендикулярного двум векторам.
Площадь параллелограмма, построенного на двух векторах, равна
модулю векторного произведения этих векторов
S
b
a
b
S = |[ a , b ]|.
S a b sin
Площадь треугольника
a
S
1
S = |[ a , b ]|.
2
25.
Смешанное произведение трех векторовc
Смешанным произведением трех векторов a , b и называется
число, получаемое следующим образом:
векторное произведение [ a , b ]
умножается скалярно на вектор c :
( a , b , c ) = ([ a , b ], c ).
Геометрически смешанное произведение по абсолютной величине
равняется объему параллелепипеда, построенного на этих векторах.
[a , b ]
V = |( a , b , c )|.
c
Объем треугольной пирамиды
b
a
1
V = |( a , b , c )|.
6
25
26.
Свойства смешанного произведения1.
([ a , b ], c ) = – ([ b , a ], c )
2.
([ a , b ], c ) = ([ b , c ], a ) = ([ c , a ], b )
3.
([ a , b ], c ) = ( a ,[ b , c ])
Условие компланарности векторов.
Если три вектора компланарны, то их смешенное произведение
равняется нулю.
[a , b]
c
a
b
( a b c) 0
26
27.
Смешанное произведение в координатной формеСмешанное произведение в координатной форме равняется
определителю третьего порядка, строками которого являются координаты
векторов
ax
( a , b , c ) = bx
cx
ay
by
cy
az
bz
cz
27
28.
Применение смешанного произведения:1. Нахождение объемов параллелепипеда и пирамиды.
2. Проверка условия компланарности трех векторов.
3. Проверка линейной независимости векторов или проверка условия,
образуют ли три вектора базис в трехмерном пространстве.
Если векторы некомпланарны, то они линейно независимы и
образуют базис. Их смешанное произведение отлично от нуля
ax
( a b c ) bx
cx
ay
by
cy
az
bz 0
cz
28

























 Математика
Математика








