Похожие презентации:
Квадратичная функция, ее график и свойства
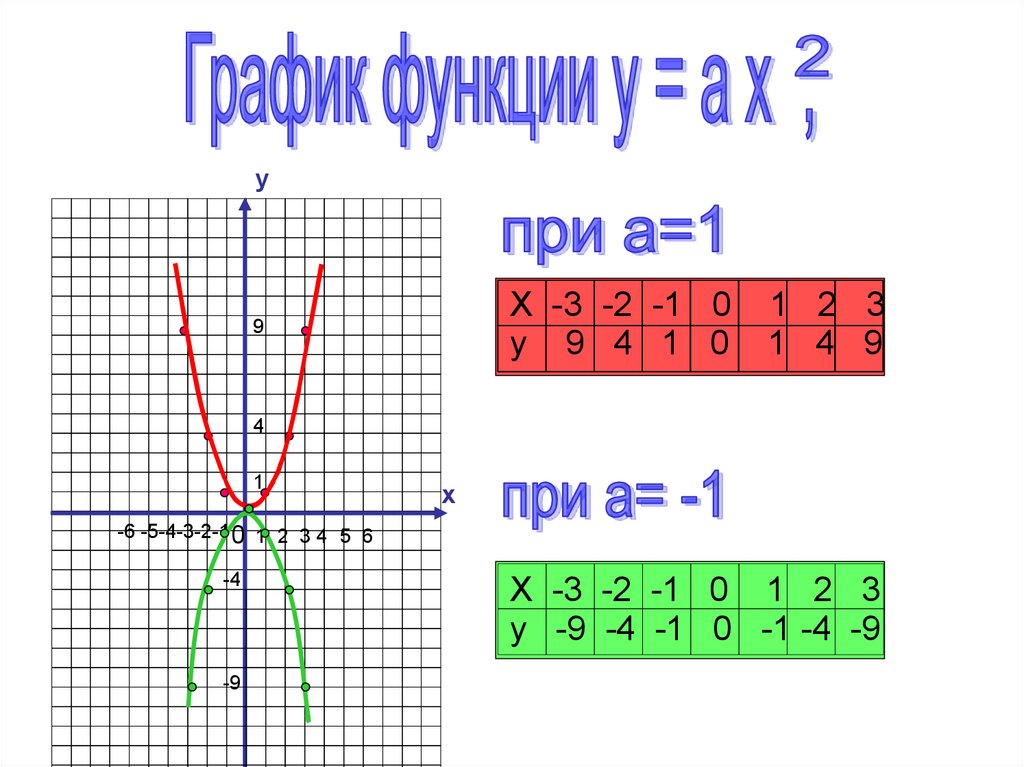
1. Квадратичная функция, ее график и свойства
2y= ax +bx + c
где: a, b, c – числа
Х – независимая переменная
а ≠0
2.
yХ -3 -2 -1 0
y 9 4 1 0
9
1 2 3
1 4 9
4
1
x
-6 -5-4-3-2-1 0 1 2 3 4 5 6
-4
-9
Х -3 -2 -1 0 1 2 3
y -9 -4 -1 0 -1 -4 -9
3.
Преобразование графика
квадратичной функции
4.
Построение графиков функцийу=aх2 и у=aх2+m
5.
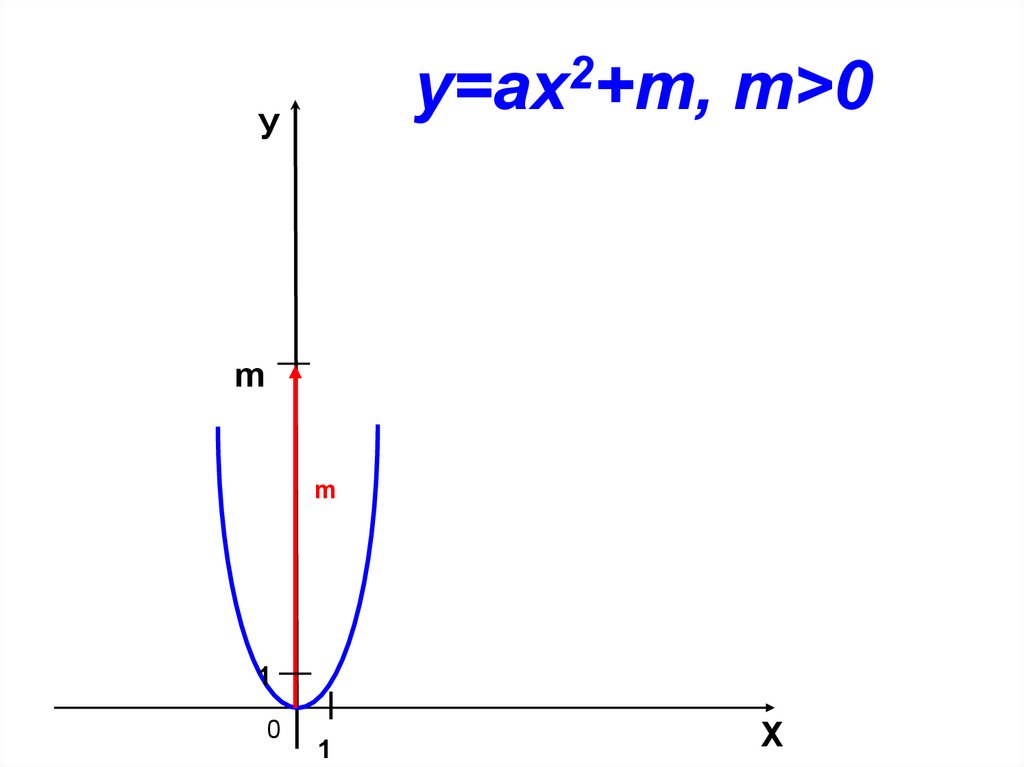
2у=aх +m, m>0
У
m
m
1
0
1
Х
6.
2у=aх +m, m<0
У
1
0
1
m
m
Х
7.
Построение графиков функцийу=aх2 и у=a(х+m)2.
8.
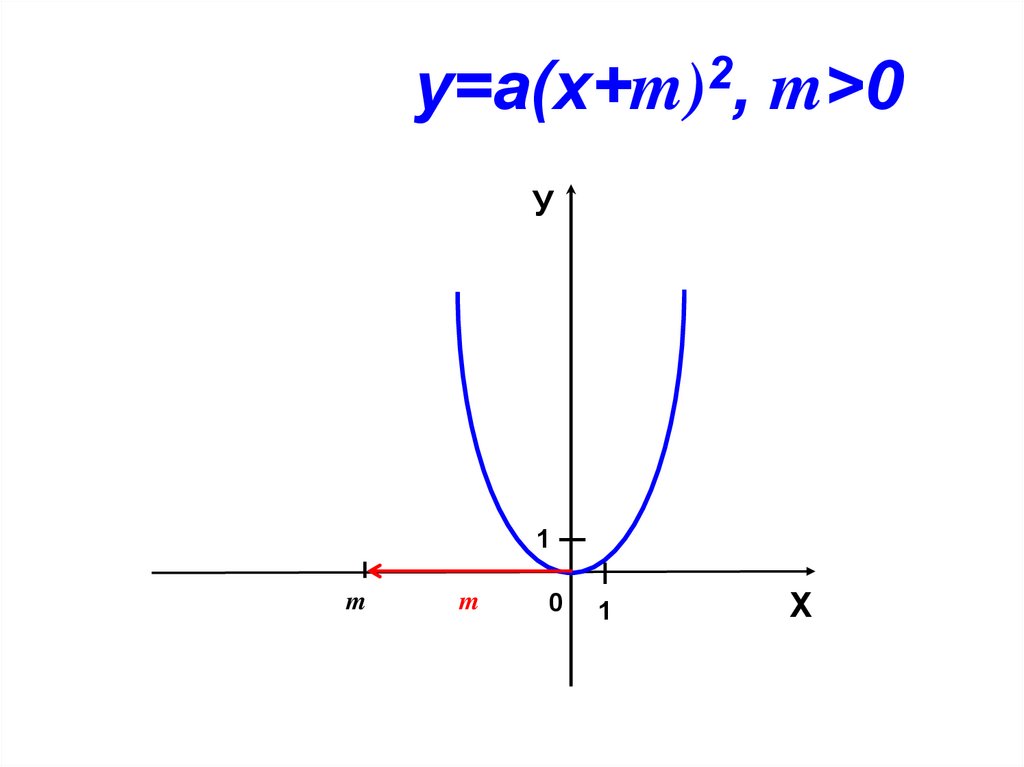
2у=a(х+m) , m>0
У
1
m
m
0
1
Х
9.
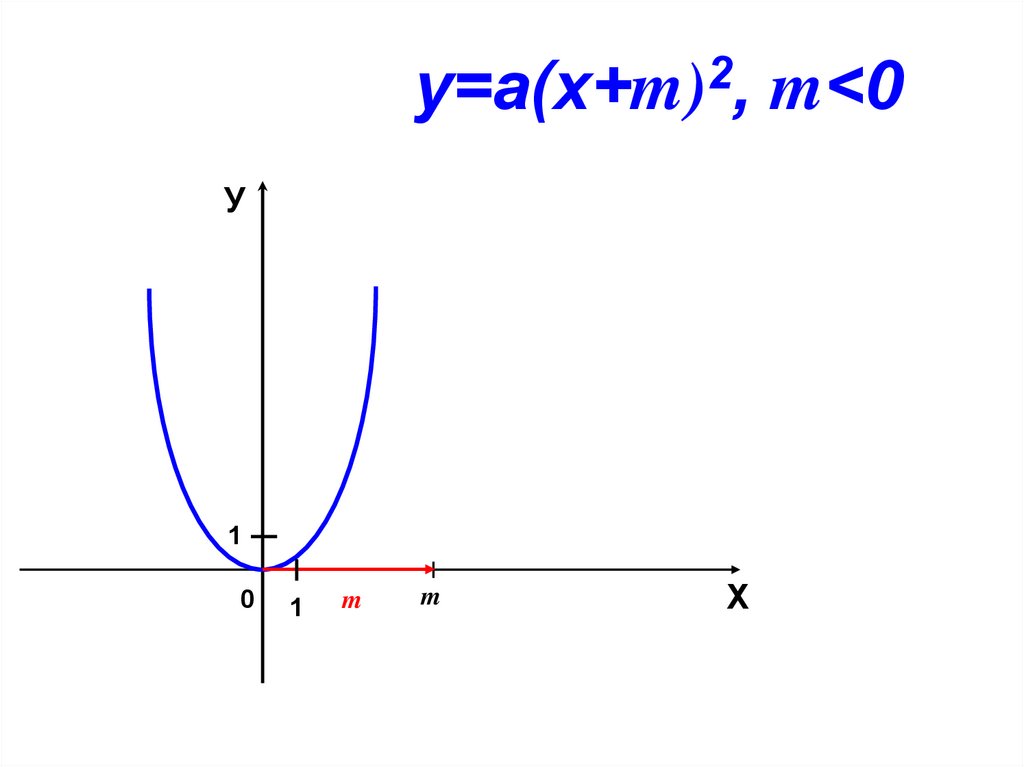
2у=a(х+m) , m<0
У
1
0
1
m
m
Х
10.
Графиком квадратичной функцииу = ах2 + bх + с является парабола,
которая получается из параболы
у = ах2 параллельным переносом.
Если коэффициент
а > 0, то
а < 0, то
ветви параболы направлены
вверх
вниз
11.
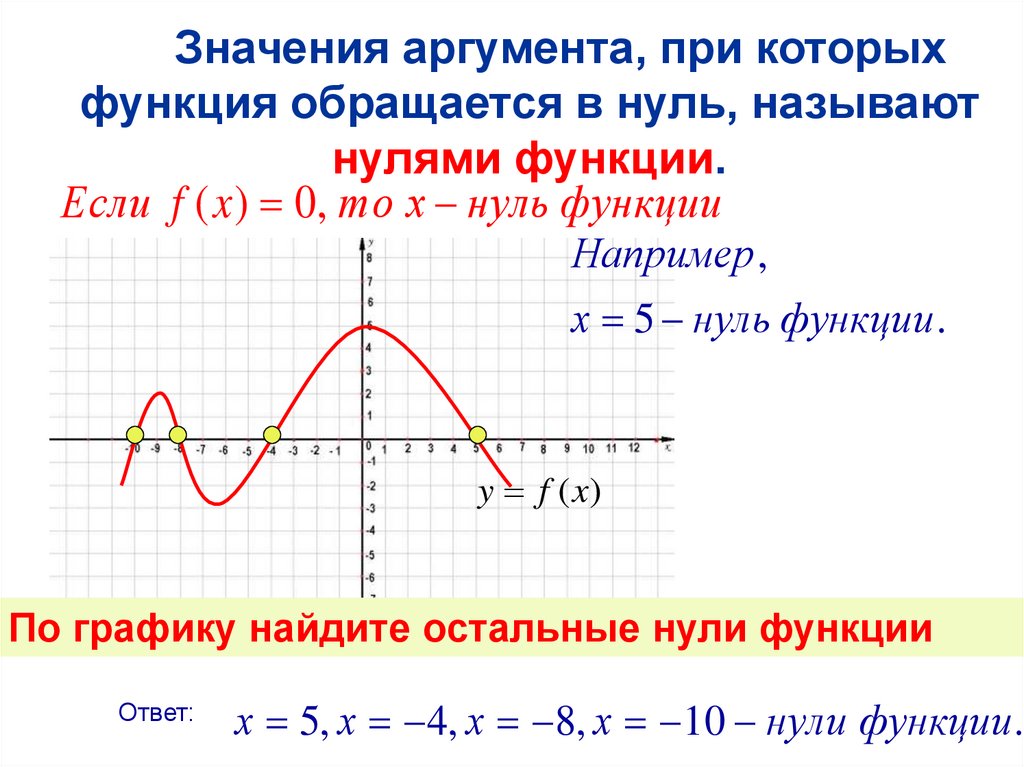
Значения аргумента, при которыхфункция обращается в нуль, называют
нулями функции.
Если f ( x ) 0, то х нуль функции
Например ,
х 5 нуль функции .
y f (x)
По графику найдите остальные нули функции
Ответ:
х 5, х 4, х 8, х 10 нули функции .
12. 2x2- 5x + 2 = 0
Найти нули функцииу=2x2- 5x + 2
2x2- 5x + 2 = 0
a = 2, b = -5, c = 2.
D = b2- 4ac = (-5)2- 4 2 2 = 9.
Так как D > 0, то уравнение имеет два корня.
Найдем их по формуле
х
5 9
b D
2 a
2 2
x
x
1
2
5 3
4
5 3
1
0,5
4
2
5 3
2
4
Ответ : х1 0,5, х2 2
13.
Дискриминантом квадратного уравненияах2 + bх + с = 0 называется выражение
b2 – 4ac
Его обозначают буквой D,
т.е.
D= b2 – 4ac
Возможны три случая:
D 0
х
b D
2 a
2 корня
D 0
1 корень
D 0
нет корней
14.
если D>0, то парабола пересекаету
ось X в двух точках
x1
x2
Х
если D=0, то парабола касается оси
X в одной точке
Вершина
у
b D b
x0
2 a
2 a
параболы
Х
x
если D<0, то парабола не пересекает
у
ось X
Х
15.
-При
ветви параболы
направлены вверх
При
ветви параболы
направлены вниз
у
b
2a
у
f(x0)
х
х
b
2a
b
абсцисса вершины параболы x 0
2a
ордината вершины параболы y y ( x )
0
0
16.
Найти координаты вершины параболыу=х2-4х+3
Вычислим координаты вершины параболы (х0;у0)
a=1,b=-4,c=3
4
b
x0
2
2 a 2
у
.
2-4∙2+3=
2
у0=y(2)=
=4-8+3=-1
.
3
0
-1
.. .
2
х
3
(2; -1)-вершина параболы
Ось
симметрии.
17. Алгоритм построения параболы у = ах2 + bх + с
График любой квадратичной функции – парабола.Алгоритм построения параболы у = ах2 + bх + с
1)Найти координаты вершины параболы по
формулам
2) построить в координатной плоскости
соответствующую точку
3)провести через вершину ось симметрии.
4)Определить направление ветвей параболы.
5) Найти нули функции и отметить их на оси Х
6)Найти координаты точки пересечения
параболы с осью у ( при х=0)
7) Если надо найти по формуле координаты
дополнительных точек.
8)Отметить эти точки и точки, симметричные им, в
координатной плоскости
9) Провести параболу
18.
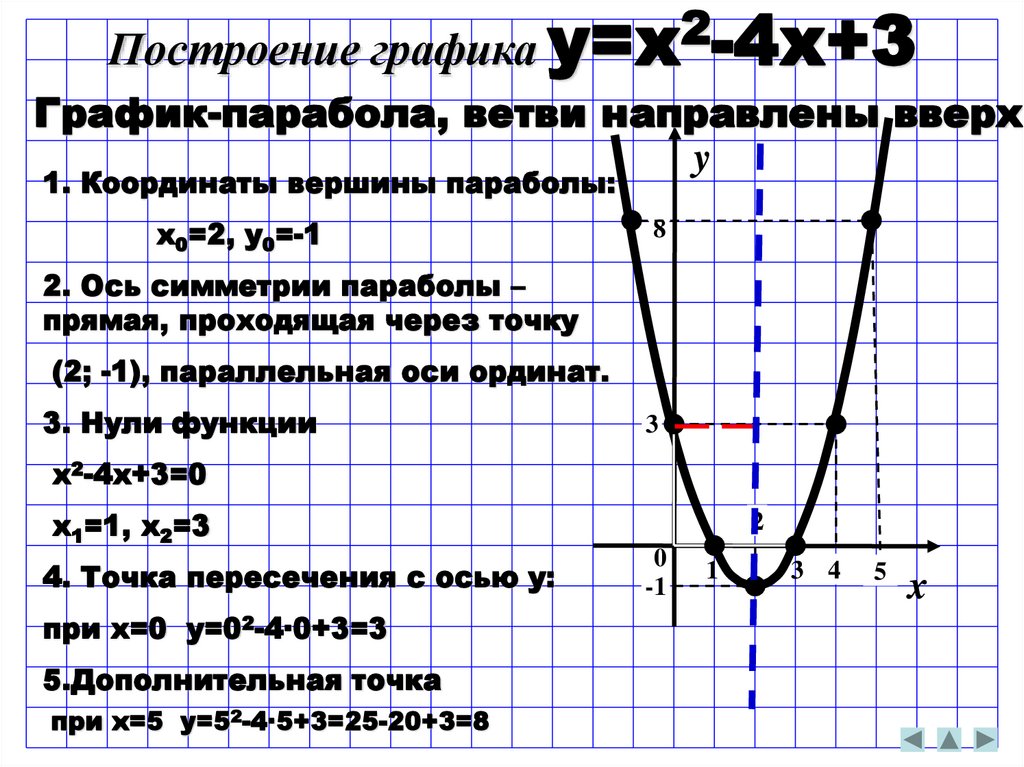
Построение графика y=x2-4x+3График-парабола, ветви направлены вверх
y
1. Координаты вершины параболы:
x0=2, y0=-1
8
2. Ось симметрии параболы –
прямая, проходящая через точку
(2; -1), параллельная оси ординат.
3. Нули функции
3
x2-4x+3=0
x1=1, x2=3
4. Точка пересечения с осью у:
при х=0 у=02-4∙0+3=3
5.Дополнительная точка
при х=5 у=52-4∙5+3=25-20+3=8
2
0
-1
1
3 4
5
x



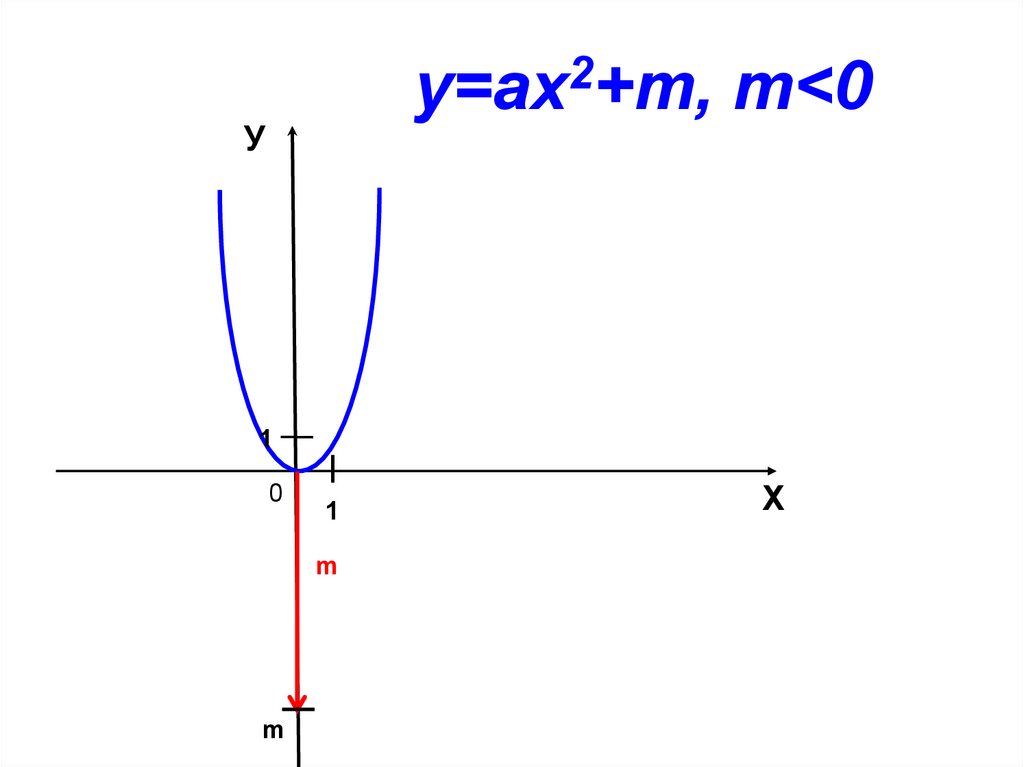









 Математика
Математика







