9 - алгебра - Презентация по алгебре на тему _Квадратичная функция, её свойства и граф

1.

Тема урока
«Квадратичная
функция, её свойства
и график»

2. Квадратичная функция

Функция, заданная формулой у = aх² + bх + c,
где х – переменная, a, b, c – данные числа,
причём a ≠ 0, называется квадратичной
функцией.
Графиком квадратичной функции
является парабола

3.

Квадратичная функция у = aх² + bх + c
1. Если а > 0, то ветки параболы направлены вверх
2. Если а < 0, то ветки параболы направлены вниз
3. Координаты вершины параболы

4.

Нули функции у = aх² + bх + c
Значение аргумента, при которых
значения функции равны нулю, называют
нулями функции.
aх² + bх + c = 0
Если D > 0, парабола имеет две точки
пересечения с осью абсцисс (ох)
Если D = 0, парабола имеет одну точку
пересечения с осью абсцисс (ох)
Если D < 0, парабола не имеет общих
точек с осью абсцисс (ох)

5.

Промежутки знакопостоянства
функции у = aх² + bх + c
Промежуток, на котором функция имеет
только положительные или только
отрицательные значения, называют
промежутком знакопостоянства функции.

6. Возрастание и убывание функции

Функцию называют возрастающей на
некотором промежутке, если для любого
значения аргумента из этого промежутка
большему значению аргумента
соответствует большее значение функции.
Функцию называють убывающей на
некотором промежутке, если для любого
значения аргумента из этого промежутка
большему значенню аргумента
соответствует меньшее значения
функции.

7.

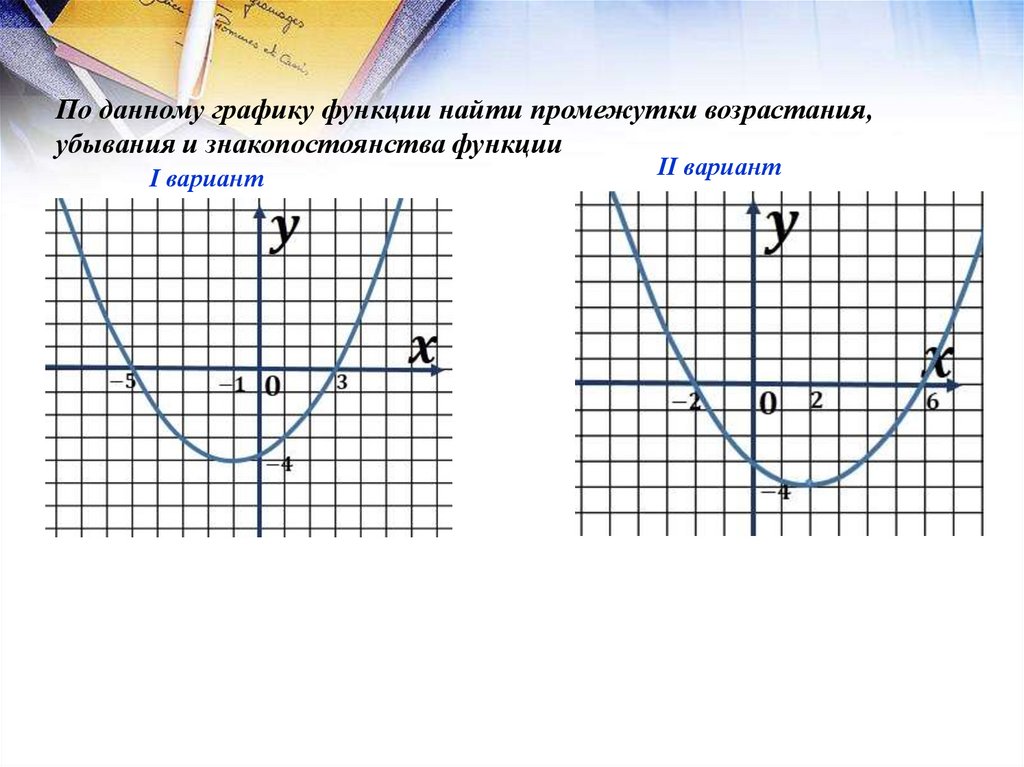
По данному графику функции найти промежутки возрастания,
убывания и знакопостоянства функции
І вариант
ІІ вариант

8.

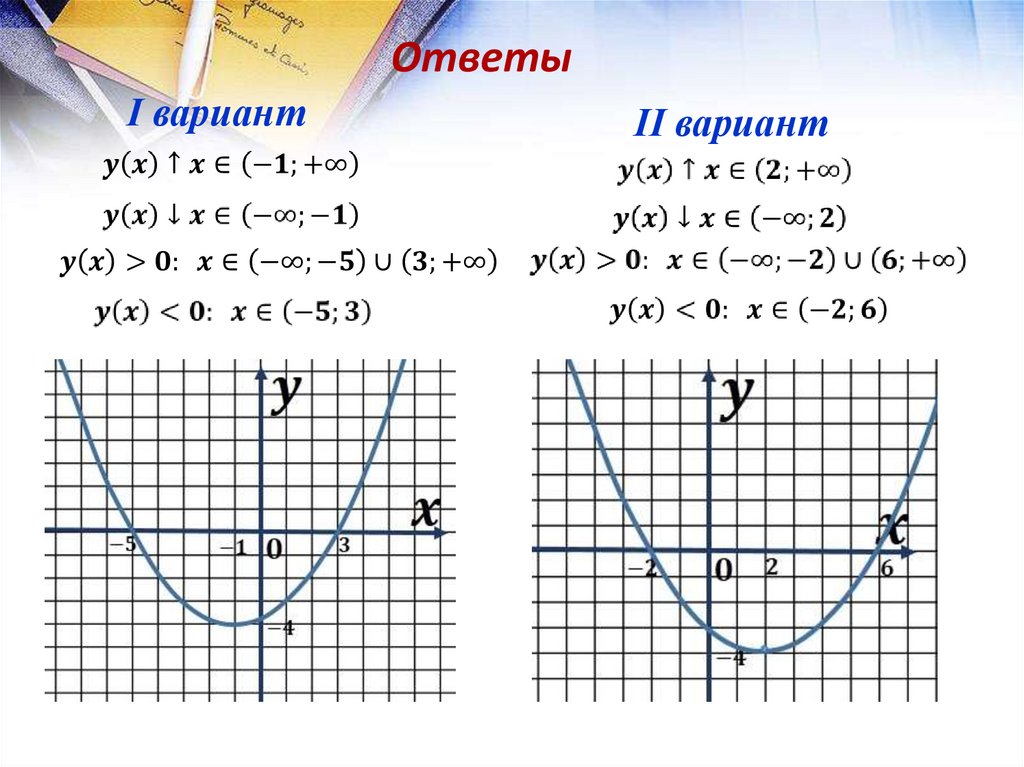
Ответы
І вариант
ІІ вариант

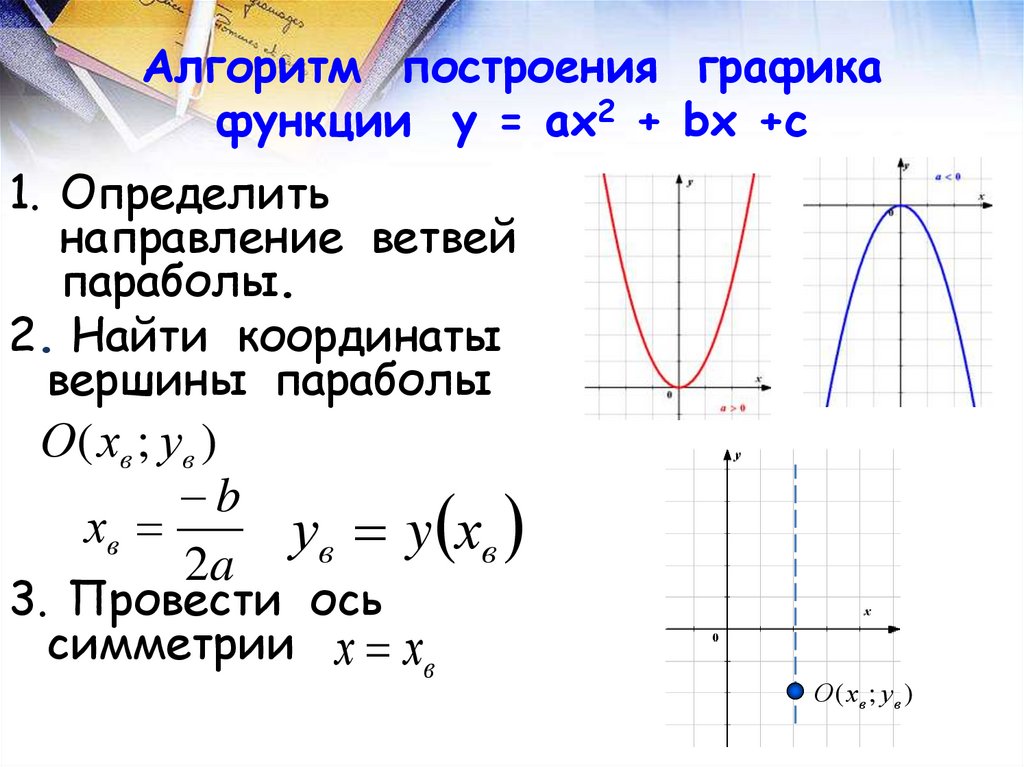
9. Алгоритм построения графика функции у = ах2 + bх +с

1. Определить
направление ветвей
параболы.
2. Найти координаты
вершины параболы
О ( хв ; ув )
b
хв
2a
ув y хв
3. Провести ось
симметрии х хв
О ( хв ; ув )

10.

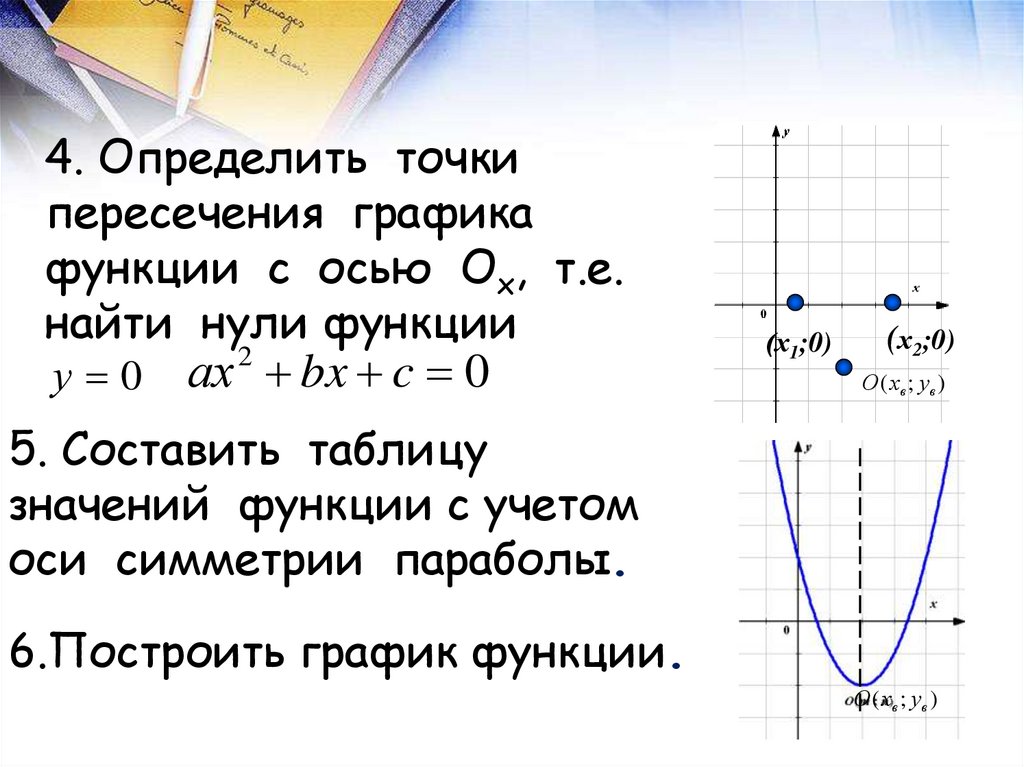
4. Определить точки
пересечения графика
функции с осью Ох, т.е.
найти нули функции
2
у 0 ах bx c 0
(х1;0)
(х2;0)
О ( хв ; ув )
5. Составить таблицу
значений функции с учетом
оси симметрии параболы.
6.Построить график функции.
О ( хв ; ув )

11.

Рассмотрим пример:
х = 2
у
8
7
6
Построить график функции
5
у = х2 – 4х + 3
4
3)
Проведем
ось
2) Найдем
4)
5)
Определим
координаты
точку
точки
1)
6)
Т.к.
Найдем
а=1,параболы
то
точку
Е Оу
симметрии
7)
Построим
график
вершины
пересечения
пересечения
светви
графика
осью
параболы
симметричную
направлены
точке
функции
х=0,
функции
у=3, значит
с осью
D(0;3)
ОхD, –
х;в ,ут
.е. хоси
2
Ох ( хнайдем
вверх.
относительно
впересечения
в)
т.е.
точка
нули
симметрии.
Е(4;3)
b
4
функции
с
осью
Оу
х
2
-6
D3
Е
2
О1 В
-5
-4
-3
-2
-1
0
х
С
1
2
О
3
4
5
хв2 4 х2 a3 0
2 1
О
( 2; 1)
2 2
2
2
у
Dв b 2 4
ac4 (2
4
) 3
4 1 31 4 2
b D
x1, 2
2a
x1 1, x2 3
В(1;0); С(3;0)

12. Свойства квадратичной функции у = ах2 + bх +с, при а>0

Свойства квадратичной функции
у = ах2 + bх +с, при а>0
D>0
1. Область
определения
2. Область
значений
3. Нули функции
4.Возрастание
убывание
функции
D=0
D( у ) R
Е ( у ) ув ;
b
b D
нулей нет
x1, 2
x1, 2
2a
2a
; xв функция убывает
xв ; функция возрастает
5.Положительны ; х х ; , у 0
1
2
; х1 х1; , у 0
е отрицательные
х ; х , y 0
значения функции 1 2
6.Наибольшее
или наименьшее
значение функции
D<0
; , y 0
унаим ув
Для у=ах2+bх+с, при а<0, заполните таблицу самостоятельно

13. Пример: Рассмотрим свойства функции у = х2 – 2х - 3

Пример:
у
Рассмотрим свойства
функции у = х2 – 2х - 3
6)
5)
4)Область
Положительные
Наименьшее
При функции:
Область
3)
Нули
1.2.
значения
значение
функция
2 –
хопределения
;1- 3
=0
хзначений
2х
принимает
функции:
функция убывает
Е
(
у
)
4
;
;
Dна
4
x
1
,
x
3
1х
1
2
промежутке
у 1; 4
+
0
возрастает
функция
3 ;
; 1
наим
Отрицательные
1;3
+
1
-4
1
-
х

14.

Ответьте на
вопросы:
1. Назовите координаты
вершины параболы;
2. Назовите ось
симметрии параболы;
3. Назовите нули
функции;
4. Назовите промежутки
возрастания и убывания
функции;
5. При каких значениях х,
значения функции
положительны, а при
каких отрицательны;
6. Назовите наибольшее
или наименьшее
значение функции.
у
4
3
2
1
-4
-3
-2
1
-1 0
-2
-3
-4
-5
2
3
4 х