Применение производных частных. Касательная плоскость и нормаль к поверхности

1.

Математический анализ
ЛЕКЦИЯ № 15
ПРИМЕНЕНИЕ
ПРОИЗВОДНЫХ
ЧАСТНЫХ

2.

§ 1. Касательная плоскость и нормаль к поверхности
Пусть функция z f ( x, y ) дифференцируема в точке М 0 х 0 , у 0 , тогда
существует касательная плоскость к графику функции в точке
х 0 , у 0 , f х 0 , у 0 .
Уравнение касательной плоскости к поверхности z f ( x, y ) в точке
М 0 х 0 , у 0 , z 0 , принадлежащей этой поверхности, определяется уравнением
(1.1)
f x x 0 , y 0 x x 0 f y x 0 , y 0 y y 0 z z 0 0 .
Нормальный
вектор
касательной
n f x x0 , y 0 , f y x0 , y 0 , 1
плоскости называется
н о р м а л ь ю к поверхности z f ( x, y ) в точке
М 0 х0 , у 0 , z 0 .
Тогда уравнение нормали к поверхности z f ( x, y ) в точке
М 0 х 0 , у 0 , z 0 имеет вид
х х0
y y0
z z0
.
(1.2)
f x x 0 , y 0 f y x 0 , y 0
1

3.

Если уравнение поверхности задано уравнением F x, y, z 0 , то уравнение
касательной плоскости в точке М 0 х 0 , у 0 , z 0 , принадлежащей этой плоскости, определяется
уравнением
Fx M 0 x x 0 Fy M 0 y y 0 Fz M 0 z z 0 0 , (1.3)
а уравнение нормали имеет вид
х х0
y y0
z z0
.
(1.4)
Fx M 0 F y M 0 Fz M 0
Пример 1. Написать уравнение касательной плоскости и нормали к параболоиду
2
z x y 2 в точке М 0 1, 2, 5 .
Решение.
Здесь
f x x, y z x 2 x , f y x, y z y 2 y .
f x 1, 2 2 , f y 1, 2 4 .
Пользуясь формулами (13.1) и (13.2), получим уравнение касательной плоскости
2 x 1 4 y 2 z 5 0
или
2x 4 y z 5 0
и уравнение нормали
х 1 y 2 z 5
.
2
4
1

4.

§ 2. Экстремум функции многих переменных
Экстремум функции многих переменных рассмотрим на функции двух
переменных.
Точка M 0 ( x0 , y0 ) называется т о ч к о й м а к с и м у м а ( м и н и м у м а )
функции z f ( x, y) ( z f ( M )) , если существует такая -окрестность точки
M 0 , для всех точек которой выполняется неравенство: f ( M ) f ( M 0 ) или
f ( x, y ) f ( x 0 , y 0 ) ( f ( M ) f ( M 0 ) , f ( x, y ) f ( x 0 , y 0 ) ) (рис. 1).
z
z
z f x, y
y
M0
x
M
y
M0
x
а)
z f x, y
M 0 точка максимума
f ( x 0 , y 0 ) максимум функции z f x, y
б)
M
M 0 точка минимума
f ( x0 , y0 ) минимум функции z f x, y
Рисунок 1

5.

Точки максимума и минимума называются т о ч к а м и
экстремума
(экстремальными
т о ч к а м и ), а значение
функции в такой точке называется экстремумом функции.
Теорема (необходимый признак экстремума дифференцируемой
функции). Если функция z f ( x, y ) дифференцируема в точке M 0 ( x0 , y0 ) и
достигает в ней экстремум, то все её частные производные первого порядка
в этой точке равны нулю, т.е.
z
0,
x
f x ( x 0 , y 0 ) 0,
M0
или
.
f
(
x
,
y
)
0
y 0 0
z
0
y
M0
Доказательство.
Предположим, y y 0 const . Тогда z f ( x, y 0 ) - функция одной
переменной x в точке x0 будет иметь экстремум.
Используя необходимое условие экстремума функции одной
переменной, получим f x ( x, y 0 ) M 0 или f x ( x0 , y0 ) 0 .
0
Аналогично можно показать, что f y ( x0 , y0 ) 0 . Теорема доказана.

6.

Точка M 0 ( x0 , y0 ) называется с т а ц и о н а р н о й т о ч к о й для функции
z f ( x, y ) , если её частные производные первого порядка в этой точке равны
нулю.
Отсюда следует, что всякая экстремальная точка дифференцируемой
функции будет и стационарной. Обратное утверждение неверно, т.е. не всякая
стационарная точка является точкой экстремума.
Например, точка M 0 (0,0) является стационарной для функции z x 3 y 3 ,
но z 0 не является экстремумом, т.к. в любой окрестности точки M 0 будут
находиться как точки в окрестности z 0 , так и точки в окрестности z 0 .
В точке экстремума функция не обязательно должна
дифференцируемой.
Например, в точке O(0,0) функция z
быть
x 2 y 2 имеет минимум, однако её
частные производные в этой точке не существуют.
Следствие. Точками экстремума могут быть либо стационарные точки, либо
точки, в которых функция не дифференцируема.
Все эти точки называются к р и т и ч е с к и м и и только они являются
«подозрительными» на экстремум.

7.

Рассмотрим достаточный признак экстремума дифференцируемой функции.
Пусть точка M 0 ( x0 , y0 ) является с т а ц и о н а р н о й , причем в этой точке и некоторой её
-окрестности
функция
z f ( x, y )
имеет
частные
производные
до
второго
порядка
включительно.
Введем обозначения значений частных производных второго порядка в точке M 0 ( x0 , y0 ) .
Пусть
2 z
2 z
2 z
, C 2 .
A 2 , B
x
y
x
M O
M O
y M O
Обозначим АС В 2 .
Теорема 1.
Если в стационарной точке M 0 ( x0 , y0 )
АС В 2 > 0, то функция
z f ( x, y ) в точке M 0 ( x0 , y0 ) имеет экстремум, причем при А 0 – max, при А 0 – min.
Теорема 2. Если в стационарной точке M 0 ( x0 , y0 ) АС В 2 < 0, то функция z f ( x, y )
в точке M 0 ( x0 , y0 ) экстремума не имеет.
Замечание. Если в стационарной точке M 0 ( x0 , y0 ) АС В 2 = 0, то вопрос о наличии
экстремума в ней остается открытым.

8.

Вывод. Чтобы исследовать функцию z f ( x, y ) на экстремум, надо:
I. Найти стационарные (критические) точки z f ( x, y ) .
z z
1) Найти
,
.
x у
z
x 0,
2) Решить систему:
z 0
у
( x 2 , y 2 ) – решения системы, тогда М 1 ( x1 , y1 ) и
Пусть ( x1 , y1 )
и
М 2 ( x 2 , y 2 ) - стационарные точки.
II. Проверим точки на экстремум с помощью достаточного условия.
2
2
2 z z z
3. Найдем
,
,
2 .
x 2 x y y
Для каждой стационарной точки найдем значения А , В , С , (например,
для точки М 1 ( x1 , y1 ) ).
2z
2z
2z
, C 2 .
A 2 , B
y
x M 1
x y M 1
M1

9.

4. Вычислим А С В 2 .
5. Для определения точек экстремума воспользуемся следующей таблицей
А
+
+
min
+
–
max
Вывод
–
экстремума нет
0
дополнительное исследование

10.

§ 3. Наибольшее и наименьшее значение функции
Пусть функция z f ( x, y) определена и непрерывна в замкнутой,
ограниченной области D , тогда она имеет в этой области наибольшее и
наименьшее значения.
Чтобы
найти
наибольшее
и
наименьшее
значения
дифференцируемой функции z f ( x, y) в ограниченной замкнутой
области D , надо:
1) найти все критические точки функции, принадлежащие области
D;
2) вычислить значения функции в этих критических точках;
3) найти наибольшее и наименьшее значения функции z f ( x, y) на
границе области;
4) сравнить все полученные значения функции и выбрать из них
наибольшее и наименьшее.

11.

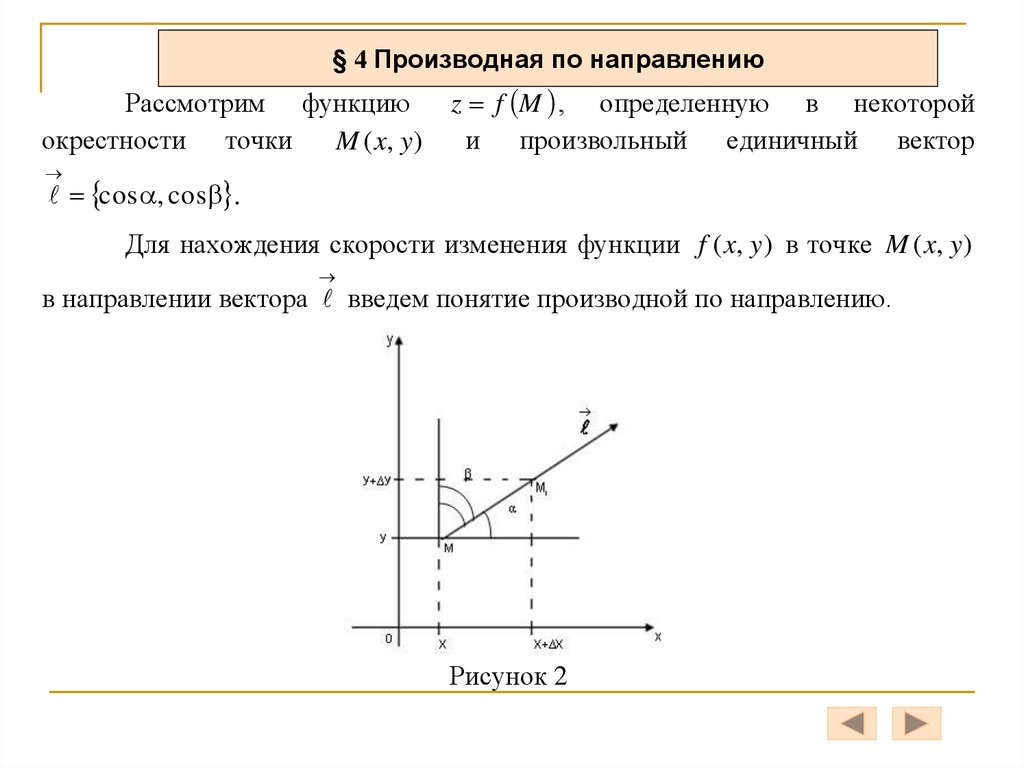
§ 4 Производная по направлению
Рассмотрим функцию
окрестности точки
M ( x, y )
z f M , определенную в некоторой
и произвольный единичный вектор
cos , cos .
Для нахождения скорости изменения функции f ( x, y ) в точке M ( x, y )
в направлении вектора введем понятие производной по направлению.
Рисунок 2

12.

На прямой, совпадающей с направлением вектора , возьмем точку
M 1 ( x х, y у ) (рис.63). Функция z f M получит при этом приращение
z f ( х х, у у) f ( x, y) .
Производной
функции
z f M
в
точке
M ( x, y ) п о
z
н а п р а в л е н и ю в е к т о р а называется предел отношения
при
0 , если он существует, и обозначается
z
дz
lim
.
0
д
Пусть функция z f M дифференцируема в точке M ( x, y ) , тогда
дz
дz
z x y x y,
дx
дy
где и - бесконечно малые функции при 0 .
Обе части равенства разделим на l . Учитывая, что
y
х
cos ,
cos ,
получим

13.

z дz
дz
cos cos cos cos .
дх
дy
В этом равенстве, перейдя к пределу при l 0 , получим
формулу производной по направлению
дz дz
дz
(1.5)
cos
cos .
д дx
дy
Аналогично определяется производная по направлению для
функции трех переменных U f ( x, y, z ) :
дU дU
дU
дU
(1.6)
cos
cos
cos .
д
дx
дy
дz

14.

§ 4 Скалярное поле. Градиент скалярного поля
Если указан закон, по которому каждой точке M области V
пространства соответствует определенное число U U (M ) , то
говорят, что в области задано с к а л я р н о е п о л е .
Если в пространстве выбрана некоторая декартовая система
координат, то задание скалярного поля эквивалентно заданию
функции трех переменных U ( M ) U ( x, y, z ) .
Поле U (M ) называется п л о с к и м , если в некоторой
декартовой системе координат оно задается функцией вида
U ( M ) U ( x, y) .
Г р а д и е н т о м скалярного поля U (M ) называется вектор
grad U , направленный по нормали к поверхности уровня поля в
сторону возрастания поля и численно равный наибольшей
производной по направлению.
В пространстве OXYZ градиент grad U вычисляется по
формуле

15.

дU дU дU
grad U
i
j
k
дx
дy
дz
или
дU дU дU
.
grad U
;
;
дx дy дz
Наибольшая скорость изменения функции U в точке M
численно равна
2
дU
дU
дU
gradU
.
дх
дz
ду
2
2
(1.7)